We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we show that any Frobenius split, smooth, projective threefold over a perfect field of characteristic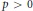 
$p\,>\,0$ is Hodge–Witt. This is proved by generalizing to the case of threefolds a well-known criterion due to 
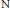$\text{N}$. Nygaard for surfaces to be Hodge-Witt. We also show that the second crystalline cohomology of any smooth, projective Frobenius split variety does not have any exotic torsion. In the last two sections we include some applications.
