We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we prove a perturbative result for a class of
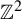${\mathbb Z}^2$
actions on Heisenberg nilmanifolds that have Diophantine properties. Along the way we prove cohomological rigidity and obtain a tame splitting for the cohomology with coefficients in smooth vector fields for such actions.
