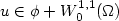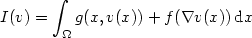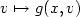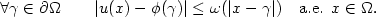1 results
A Haar-Rado type theorem for minimizersin Sobolev spaces
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 4 / October 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 1133-1143
- Print publication:
- October 2011
-
- Article
- Export citation
-
Let $u\in\phi+ W_0^{1,1}(\Omega)$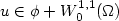
be a minimum for$\[I(v)=\int_{\Omega}g(x,v(x))+f(\nabla v(x))\,{\rm d}x\]$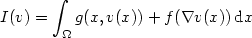
where f is convex, $v\mapsto g(x,v)$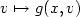
is convex for a.e. x. We prove that u shares the same modulus of continuity of ϕ whenever Ω is sufficiently regular, the right derivative of g satisfies a suitable monotonicity assumption and the following inequality holds $\forall \gamma\in\partial\Omega\qquad |u(x)-\phi(\gamma)|\le\omega(|x-\gamma|) \quad\text{a.e. }x\in\Omega.$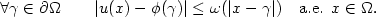
This result generalizes the classical Haar-Rado theorem forLipschitz functions.
