1 results
Trace inequalities and kinematic metrics
- Part of
-
- Journal:
- Robotica , First View
- Published online by Cambridge University Press:
- 12 September 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Kinematics remains one of the cornerstones of robotics, and over the decade, Robotica has been one of the venues in which groundbreaking work in kinematics has always been welcome. A number of works in the kinematics community have addressed metrics for rigid-body motions in multiple different venues. An essential feature of any distance metric is the triangle inequality. Here, relationships between the triangle inequality for kinematic metrics and so-called trace inequalities are established. In particular, we show that the Golden-Thompson inequality (a particular trace inequality from the field of statistical mechanics) which holds for Hermitian matrices remarkably also holds for restricted classes of real skew-symmetric matrices. We then show that this is related to the triangle inequality for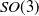
$SO(3)$ and 
$SO(4)$ metrics.
