Nonlinear stratified spindown of an along-isobath current over an insulated slope is shown to develop asymmetries in the vertical circulation and vertical relative vorticity field. During spindown, cyclonic vorticity is weakened to a greater extent than anticyclonic vorticity near the boundary because of buoyancy advection. As a consequence, Ekman pumping is weakened over Ekman suction. Momentum advection can weaken Ekman pumping and strengthen Ekman suction. Time-dependent feedback between the geostrophic flow and the frictional secondary circulation induces asymmetry in cyclonic and anticyclonic vorticity away from the boundary. Buoyancy advection over a slope can modify the secondary circulation such that anticyclonic vorticity decays faster than cyclonic vorticity outside the boundary layer. In contrast, momentum advection can cause cyclonic vorticity to spin down faster than anticyclonic vorticity. A scaling and analytical solutions are derived for when buoyancy advection over a slope can have a more significant impact than momentum advection on these asymmetries. In order to test this scaling and analytical solutions, numerical experiments are run in which both buoyancy and momentum advection are active. These solutions are contrasted with homogeneous or stratified spindown over a flat bottom, in which momentum advection controls the asymmetries. These results are applied to ocean currents over continental shelves and slopes.

Direct numerical simulations of free convection over a smooth, heated plate are used to investigate unbounded, unsteady turbulent convection. Four different boundary conditions are considered: free-slip or no-slip walls, and constant buoyancy or constant buoyancy flux. It is first shown that, after the initial transient, the vertical structure agrees with observations in the atmospheric boundary layer and predictions from classical similarity theory. A quasi-steady inner layer and a self-preserving outer layer are clearly distinguished, with an overlap region between them of constant turbulent buoyancy flux. The extension of the overlap region reached in our simulations is more than 100 wall units 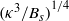$ \mathop{ ({\kappa }^{3} / {B}_{s} )}\nolimits ^{1/ 4} $, where 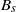${B}_{s} $ is the surface buoyancy flux and $\kappa $ the corresponding molecular diffusivity (the Prandtl number is one). The buoyancy fluctuation inside the overlap region already exhibits the $\ensuremath{-} 1/ 3$ power-law scaling with height for the four types of boundary conditions, as expected in the local, free-convection regime. However, the mean buoyancy gradient and the vertical velocity fluctuation are still evolving toward the corresponding power laws predicted by the similarity theory. The second major result is that the relation between the Nusselt and Rayleigh numbers agrees with that reported in Rayleigh–Bénard convection when the heated plate is interpreted as half a convection cell. The range of Rayleigh numbers covered in the simulations is then 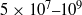$5\ensuremath{\times} 1{0}^{7} \text{{\ndash}} 1{0}^{9} $. Further analogies between the two problems indicate that knowledge can be transferred between steady Rayleigh–Bénard and unsteady convection. Last, we find that the inner scaling based on 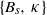$\{ {B}_{s} , \hspace{0.167em} \kappa \} $ reduces the effect of the boundary conditions to, mainly, the diffusive wall layer, the first 10 wall units. There, near the plate, free-slip conditions allow stronger mixing than no-slip ones, which results in 30 % less buoyancy difference between the surface and the overlap region and 30–40 % thinner diffusive sublayers. However, this local effect also entails one global, substantial effect: with an imposed buoyancy, free-slip systems develop a surface flux 60 % higher than that obtained with no-slip walls, which implies more intense turbulent fluctuations across the whole boundary layer and a faster growth.