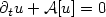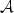This article is devoted to the study of the finite element approximation for a nonlocal nonlinear parabolic problem. Using a linearised Crank-Nicolson Galerkin finite element method for a nonlinear reaction-diffusion equation, we establish the convergence and error bound for the fully discrete scheme. Moreover, important results on exponential decay and vanishing of the solutions in finite time are presented. Finally, some numerical simulations are presented to illustrate our theoretical analysis.

New numerical techniques are presented for the solution of the two-dimensional time fractional evolution equation in the unit square. In these methods, Galerkin finite element is used for the spatial discretization, and, for the time stepping, new alternating direction implicit (ADI) method based on the backward Euler method combined with the first order convolution quadrature approximating the integral term are considered. The ADI Galerkin finite element method is proved to be convergent in time and in the L2 norm in space. The convergence order is 𝓞(k|ln k| + hr), where k is the temporal grid size and h is spatial grid size in the x and y directions, respectively. Numerical results are presented to support our theoretical analysis.

Arbitrage-free prices u of European contracts on risky assets whoselog-returns are modelled by Lévy processes satisfya parabolic partial integro-differential equation (PIDE) $\partial_t u + {\mathcal{A}}[u] = 0$ .This PIDE is localized tobounded domains and the error due to this localization isestimated. The localized PIDE is discretized by theθ-scheme in time and a wavelet Galerkin method with N degrees of freedom in log-price space. The dense matrix for ${\mathcal{A}}$ can be replaced by a sparse matrix in the wavelet basis, and the linear systemsin each implicit time step are solved approximativelywith GMRES in linear complexity. The total work of the algorithm for M time steps is bounded byO(MN(log(N))2) operations and O(Nlog(N)) memory.The deterministic algorithm gives optimal convergence rates (up to logarithmic terms) for the computed solutionin the same complexity as finite difference approximationsof the standard Black–Scholes equation.Computational examples for various Lévy price processes are presented.