Let {We}e∈ω be a standard enumeration of the recursively enumerable (r.e.) subsets of ω = {0,1,2,…}. The lattice of recursively enumerable sets,  , is the structure ({We}e∈ω,∪,∩). ≡ is a congruence relation on
, is the structure ({We}e∈ω,∪,∩). ≡ is a congruence relation on  if ≡ is an equivalence relation on
if ≡ is an equivalence relation on  and if for all U, U′ ∈
and if for all U, U′ ∈  and V, V′ ∈
and V, V′ ∈  , if U ≡ U′ and V ≡ V′, then U ∪ V ≡ U′ ∪ V′ and U ∩ V ≡ U′ ∩ V′. [U] = {V ∈
, if U ≡ U′ and V ≡ V′, then U ∪ V ≡ U′ ∪ V′ and U ∩ V ≡ U′ ∩ V′. [U] = {V ∈ | V ≡ U} is the equivalence class of U. If ≡ is a congruence relation on
| V ≡ U} is the equivalence class of U. If ≡ is a congruence relation on  , the elements of the quotient lattice
, the elements of the quotient lattice  / ≡ are the equivalence classes of ≡. [U] ∪ [V] is defined as [U ∪ V], and [U] ∩ [V] is defined as [U ∩ V]. We say that a congruence relation ≡ on
/ ≡ are the equivalence classes of ≡. [U] ∪ [V] is defined as [U ∪ V], and [U] ∩ [V] is defined as [U ∩ V]. We say that a congruence relation ≡ on  is
is  if {(i, j)| Wi ≡ Wj} is
if {(i, j)| Wi ≡ Wj} is  . Define =* by putting Wi, =* Wj if and only if (Wi − Wj)∪ (Wj − Wi) is finite. Then =* is a
. Define =* by putting Wi, =* Wj if and only if (Wi − Wj)∪ (Wj − Wi) is finite. Then =* is a  congruence relation. If D is any
congruence relation. If D is any  set, then we can define a
set, then we can define a  congruence relation
congruence relation 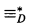 by putting Wi
by putting Wi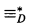 Wj if and only if Wi ∩ D =* Wj ∩D. By Hammond [2], a congruence relation ≡ ⊇ =* is
Wj if and only if Wi ∩ D =* Wj ∩D. By Hammond [2], a congruence relation ≡ ⊇ =* is  if and only if ≡ is equal to
if and only if ≡ is equal to 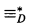 for some
for some  set D.
set D.
The Friedberg splitting theorem [1] asserts that if A is any recursively enumerable set, then there exist disjoint recursively enumerable sets A0 and A1 such that A = A0∪ A1 and such that for any recursively enumerable set B



 set, then we can define a
set, then we can define a 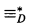 by putting W
by putting W