1 results
An invariance principle in k-dimensional extended renewal theory
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 3 / September 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 567-574
- Print publication:
- September 1979
-
- Article
- Export citation
-
Let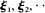
·be a sequence of k -dimensional i.i.d. random vectors and define the first-passage times 
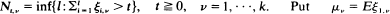for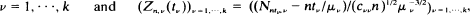 
where (cvτ)v, τ= 1,· ··,k is the covariance matrix of 
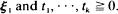In this paper the weak convergence of Zn in (D[0, ∞))k is proved under the assumption 
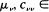(0,∞) for all v = 1, ···, k. We deduce the result from the Donsker invariance principle by means of Theorem 5.5 of Billingsley (1968). This method is also used to derive a limit theorem for the first-exit time Mn = min{Nnt 
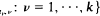for fixed t1,···, tk > 0. The second result is an extension of a theorem of Hunter (1974) whose method of proof applies only if Ρ (ξ1
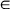[0,∞)k) = 1 and μ ν = tv for all v = 1, ···, k.
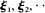·be a sequence of 
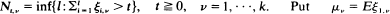for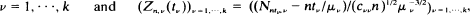 
where (
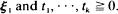In this paper the weak convergence of Z
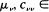(0,∞) for all 
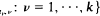for fixed 
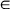[0,∞)