1 results
Coefficients of ergodicity: structure and applications
-
- Journal:
- Advances in Applied Probability / Volume 11 / Issue 3 / September 1979
- Published online by Cambridge University Press:
- 01 July 2016, pp. 576-590
- Print publication:
- September 1979
-
- Article
- Export citation
-
The concept of ‘coefficient of ergodicity’, τ(P), for a finite stochastic matrix P, is developed from a standpoint more general and less standard than hitherto, albeit synthesized from ideas in existing literature. Several versions of such a coefficient are studied theoretically and by numerical examples, and usefulness in applications compared from viewpoints which include the degree to which extension to more general matrices is possible. Attention is given to the less familiar spectrum localization property: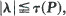
where λ is any non-unit eigenvalue of P. The essential purpose is exposition and unification, with the aid of simple informal proofs.
where λ is any non-unit eigenvalue of 