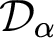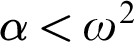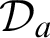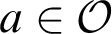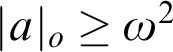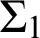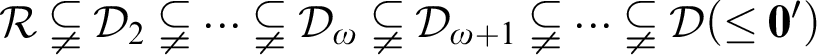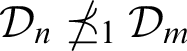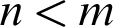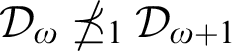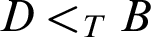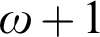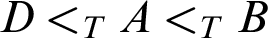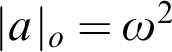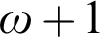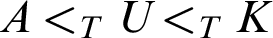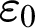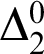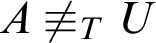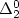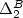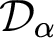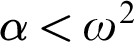In this thesis, we study Turing degrees in the context of classical recursion theory. What we are interested in is the partially ordered structures $\mathcal {D}_{\alpha }$ for ordinals $\alpha <\omega ^2$ and 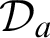$\mathcal {D}_{a}$ for notations 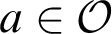$a\in \mathcal {O}$ with 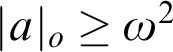$|a|_{o}\geq \omega ^2$ .

The dissertation is motivated by the 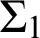$\Sigma _{1}$ -elementary substructure problem: Can one structure in the following structures 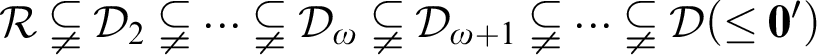$\mathcal {R}\subsetneqq \mathcal {D}_{2}\subsetneqq \dots \subsetneqq \mathcal {D}_{\omega }\subsetneqq \mathcal {D}_{\omega +1}\subsetneqq \dots \subsetneqq \mathcal {D(\leq \textbf {0}')}$ be a $\Sigma _{1}$ -elementary substructure of another? For finite levels of the Ershov hierarchy, Cai, Shore, and Slaman [Journal of Mathematical Logic, vol. 12 (2012), p. 1250005] showed that 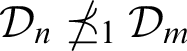$\mathcal {D}_{n}\npreceq _{1}\mathcal {D}_{m}$ for any 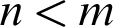$n < m$ . We consider the problem for transfinite levels of the Ershov hierarchy and show that 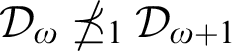$\mathcal {D}_{\omega }\npreceq _{1}\mathcal {D}_{\omega +1}$ . The techniques in Chapters 2 and 3 are motivated by two remarkable theorems, Sacks Density Theorem and the d.r.e. Nondensity Theorem.

In Chapter 1, we first briefly review the background of the research areas involved in this thesis, and then review some basic definitions and classical theorems. We also summarize our results in Chapter 2 to Chapter 4. In Chapter 2, we show that for any $\omega $ -r.e. set D and r.e. set B with 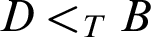$D<_{T}B$ , there is an 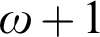$\omega +1$ -r.e. set A such that 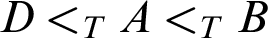$D<_{T}A<_{T}B$ . In Chapter 3, we show that for some notation a with 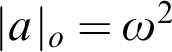$|a|_{o}=\omega ^{2}$ , there is an incomplete 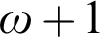$\omega +1$ -r.e. set A such that there are no a-r.e. sets U with 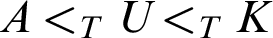$A<_{T}U<_{T}K$ . In Chapter 4, we generalize above results to higher levels (up to 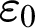$\varepsilon _{0}$ ). We investigate Lachlan sets and minimal degrees on transfinite levels and show that for any notation a, there exists a 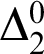$\Delta ^{0}_{2}$ -set A such that A is of minimal degree and 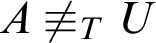$A\not \equiv _T U$ for all a-r.e. sets U.

Abstract prepared by Cheng Peng.

E-mail: [email protected]

The first-value operator assigns to any sequence of partial functions of the same type a new such function. Its domain is the union of the domains of the sequence functions, and its value at any point is just the value of the first function in the sequence which is defined at that point. In this paper, the first-value operator is applied to establish hierarchies of classes of functions under various settings. For effective sequences of computable discrete functions, we obtain a hierarchy connected with Ershov's one within $\Delta^{0}_2$. The non-effective version over real functions is connected with the degrees of discontinuity and yields a hierarchy related to Hausdorff's difference hierarchy in the Borel class $\Delta^{B}_2$. Finally, the effective version over approximately computable real functions forms a hierarchy which provides a useful tool in computable analysis.