We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This paper contributes to the study of Engel structures and their classification. The main result introduces the notion of a loose family of Engel structures and shows that two such families are Engel homotopic if and only if they are formally homotopic. This implies a complete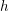 
$h$-principle when auxiliary data is fixed. As a corollary, we show that Lorentz and orientable Cartan prolongations are classified up to homotopy by their formal data.
