We give a new proof of Faltings's 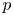 $p$-adic Eichler–Shimura decomposition of the modular curves via Bernstein–Gelfand–Gelfand (BGG) methods and the Hodge–Tate period map. The key property is the relation between the Tate module and the Faltings extension, which was used in the original proof. Then we construct overconvergent Eichler–Shimura maps for the modular curves providing ‘the second half’ of the overconvergent Eichler–Shimura map of Andreatta, Iovita and Stevens. We use higher Coleman theory on the modular curve developed by Boxer and Pilloni to show that the small-slope part of the Eichler–Shimura maps interpolates the classical
$p$-adic Eichler–Shimura decomposition of the modular curves via Bernstein–Gelfand–Gelfand (BGG) methods and the Hodge–Tate period map. The key property is the relation between the Tate module and the Faltings extension, which was used in the original proof. Then we construct overconvergent Eichler–Shimura maps for the modular curves providing ‘the second half’ of the overconvergent Eichler–Shimura map of Andreatta, Iovita and Stevens. We use higher Coleman theory on the modular curve developed by Boxer and Pilloni to show that the small-slope part of the Eichler–Shimura maps interpolates the classical 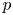 $p$-adic Eichler–Shimura decompositions. Finally, we prove that overconvergent Eichler–Shimura maps are compatible with Poincaré and Serre pairings.
$p$-adic Eichler–Shimura decompositions. Finally, we prove that overconvergent Eichler–Shimura maps are compatible with Poincaré and Serre pairings.