1 results
Blocking probabilities for large multirate erlang loss systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 997-1009
- Print publication:
- December 1993
-
- Article
- Export citation
-
This paper is concerned with the computation of asymptotic blocking probabilities for a generalized Erlangian system which results when M independent Poisson streams of traffic with rates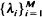
access a trunk group of C circuits with traffic from stream k requiring Ak circuits which are simultaneously held and released after a time which is randomly distributed with unit mean and independent of earlier arrivals and holding times. A call from stream k is lost if on arrival less than Ak circuits are available. Although exact expressions for the blocking probabilities are known, their computation is unwieldy for even moderate-sized switches. It is shown that as the size of the switch increases in that both the traffic rates and trunk capacity are scaled together, simple asymptotic expressions for the blocking probabilities are obtained. In particular the expression is different for light, moderate and heavy loads. The approach is via exponential centering and large deviations and provides a unified framework for the analysis.
access a trunk group of 