1 results
The characterization of distributions by order statistics and record values — a unified approach
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 326-334
- Print publication:
- June 1984
-
- Article
- Export citation
-
It is shown that, in some particular cases, it is equivalent to characterize a continuous distribution by properties of records and by properties of order statistics. As an application, we give a simple proof that if two successive jth record values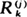
and 
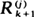associated to an i.i.d. sequence are such that 
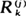and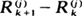 
are independent, then the sequence has to derive from an exponential distribution (in the continuous case). The equivalence breaks up for discrete distributions, for which we give a proof that the only distributions such that Xk, n and Xk+1, n – Xk, n are independent for some k ≧ 2 (where Xk, n is the kth order statistic of X1, ···, Xn) are degenerate.
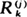and 
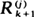associated to an i.i.d. sequence are such that 
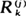and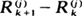 
are independent, then the sequence has to derive from an exponential distribution (in the continuous case). The equivalence breaks up for discrete distributions, for which we give a proof that the only distributions such that 