We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This paper extends a result of Godambe's theory of parametric estimation for discrete-time stochastic processes to the continuous-time case. Let P ={P} be a family of probability measures such that (Ω, F, P) is complete, (Ft, t≧0) is a standard filtration, and X = (Xt Ft, t ≧ 0) is a semimartingale for every P ∈ P. For a parameter θ (Ρ), suppose Xt = Vt,θ + Ht,θ where the Vθ process is predictable and locally of bounded variation and the Hθ process is a local martingale. Consider estimating equations for θ of the form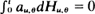 
process is predictable. Under regularity conditions, an optimal form for α θ in the sense of Godambe (1960) is determined. When Vt,θ is linear in θ the optimal 
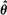, corresponds to certain maximum likelihood or least squares estimates derived previously in special cases. Asymptotic properties of 
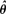, are discussed.
