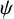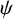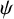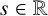1 results
JARNÍK TYPE THEOREMS ON MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 391-405
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Let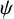
$\psi $ be a decreasing function. We prove zero-infinity Hausdorff measure criteria for the set of dual 
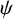$\psi $-approximable points and for the set of inhomogeneous multiplicative 
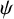$\psi $-approximable points on nondegenerate planar curves. Our results extend theorems of Huang [‘Hausdorff theory of dual approximation on planar curves’, J. reine angew. Math. 740 (2018), 63–76] and Beresnevich and Velani [‘A note on three problems in metric Diophantine approximation’, in: Recent Trends in Ergodic Theory and Dynamical Systems, Contemporary Mathematics, 631 (American Mathematical Society, Providence, RI, 2015), 211–229] from s-Hausdorff measure, where 
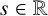$s\in \mathbb R$, to the more general g-Hausdorff measure, where g is a suitable class of dimension functions.
