1 results
Paths in a random digital tree: limiting distributions
-
- Journal:
- Advances in Applied Probability / Volume 18 / Issue 1 / March 1986
- Published online by Cambridge University Press:
- 01 July 2016, pp. 139-155
- Print publication:
- March 1986
-
- Article
- Export citation
-
We study a rule of growing a sequence {tn} of finite subtrees of an infinite m-ary tree T. Independent copies {ω (n)} of a Bernoulli-type process ω on m letters are used to trace out a sequence
of paths in T. The tree tn is obtained by cutting each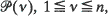 
, at the first node such that at most σ paths out of 
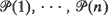, pass through it. Denote by Hn the length of the longest path, hn the length of the shortest path, and Ln the length of the randomly chosen path in tn. It is shown that, in probability, Hn – logan = O(1), hn – logb (n/log n) = 0(1), (or hn – logb (n/log log n) = O(1)), and that 
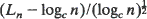is asymptotically normal. The parameters a, b, c depend on the distribution of ω and, in case of a, also on σ. These estimates describe respectively the worst, the best and the typical case behavior of a ‘trie’ search algorithm for a dictionary-type information retrieval system, with σ being the capacity of a page.
of paths in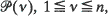 
, at the first node such that at most 
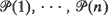, pass through it. Denote by 
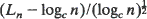is asymptotically normal. The parameters 