Computer scientists have introduced ‘paging algorithms' which are a special class of Markov chains on permutations known, in probability theory, as ‘libraries': books being placed on a shelf T (T is an infinite interval of the set Z of the integers) and a policy ρ : T → T such that ρ (t) < t being chosen, a book b placed at t ∊ T is selected with probability pb, it is removed and replaced at ρ (t) prior to next removal. The different arrangements of books on the shelf are the states of the Markov chain. In this paper we prove that, if the shelf is not bounded on the left, any library (i.e. for any policy ρ and any probability ρ on the books) is transient.

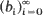Books being placed on a shelf, a book bi is selected with probability pi, it is removed and replaced at the left-hand end of the shelf prior to next removal. The different arrangements of books on the shelf are considered as states in a Markov chain, known as a Tsetlin library. In this paper, we establish the necessary and sufficient condition of transience for some extensions of this chain.

In order to study the transience of Hendricks libraries, we introduce and study a special class of Markov chains, the Tsetlin d-piles, generalizing Tsetlin libraries and briefly defined as follows: a 1-pile is a Tsetlin library and a d-pile is a Tsetlin library where each book is replaced by a (d − 1)-pile. We give a stationary measure of these chains and establish the necessary and sufficient conditions for positive recurrence and transience. Finally, the study of d-piles allows us to determine a sufficient condition for transience of quite a large class of Hendricks libraries.