We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the threshold-one contact process, the threshold-one voter model and the threshold-one voter model with positive spontaneous death on homogeneous trees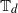 
$\mathbb{T}_d$
, 
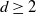$d\ge 2$
. Mainly inspired by the corresponding arguments for the contact process, we prove that the complete convergence theorem holds for these three systems under strong survival. When the system survives weakly, complete convergence may also hold under certain transition and/or initial conditions.
