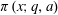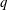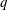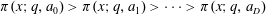As pointed out by Alexandre Bailleul, the paper mentioned in the title contains a mistake in Theorem 2.2. The hypothesis on the linear relation of the almost periods is not sufficient. In this note, we fix the problem and its minor consequences on other results in the same paper.

We generalize current known distribution results on Shanks–Rényi prime number races to the case where arbitrarily many residue classes are involved. Our method handles both the classical case that goes back to Chebyshev and function field analogues developed in the recent years. More precisely, let $\unicode[STIX]{x1D70B}(x;q,a)$ be the number of primes up to $x$ that are congruent to $a$ modulo $q$. For a fixed integer $q$ and distinct invertible congruence classes $a_{0},a_{1},\ldots ,a_{D}$, assuming the generalized Riemann Hypothesis and a weak version of the linear independence hypothesis, we show that the set of real $x$ for which the inequalities $\unicode[STIX]{x1D70B}(x;q,a_{0})>\unicode[STIX]{x1D70B}(x;q,a_{1})>\cdots >\unicode[STIX]{x1D70B}(x;q,a_{D})$ are simultaneously satisfied admits a logarithmic density.

We study a function field analog of Chebyshev’s bias. Our results, as well as their proofs, are similar to those of Rubinstein and Sarnak in the case of the rational number field. Following Rubinstein and Sarnak, we introduce the grand simplicity hypothesis (GSH), a certain hypothesis on the inverse zeros of Dirichlet L-series of a polynomial ring over a finite field. Under this hypothesis, we investigate how primes, that is, irreducible monic polynomials in a polynomial ring over a finite field, are distributed in a given set of residue classes modulo a fixed monic polynomial. In particular, we prove under the GSH that, like the number field case, primes are biased toward quadratic nonresidues. Unlike the number field case, the GSH can be proved to hold in some cases and can be violated in some other cases. Also, under the GSH, we give the necessary and sufficient conditions for which primes are unbiased and describe certain central limit behaviors as the degree of modulus under consideration tends to infinity, all of which have been established in the number field case by Rubinstein and Sarnak.