We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A simple proof is given for the fact that for 
$m$ a non-negative integer, a function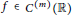 
$f\,\in \,{{C}^{(m)}}\,(\mathbb{R})$, and an arbitrary positive continuous function 
$\in$, there is an entire function 
$g$ such that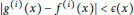 
$\left| {{g}^{(i)}}(x)\,-\,{{f}^{(i)}}(x) \right|\,<\,\in (x)$, for all 
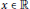$x\,\in \,\mathbb{R}$ and for each 
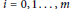$i\,=\,0,\,1\,.\,.\,.\,,\,m$. We also consider the situation where 
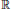$\mathbb{R}$ is replaced by an open interval.
