In this paper, a bilinear Streamline-Diffusion finite element method on Bakhvalov-Shishkin mesh for singularly perturbed convection – diffusion problem is analyzed. The method is shown to be convergent uniformly in the perturbation parameter ∈ provided only that ∈ ≤ N–1. An 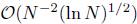 convergent rate in a discrete streamline-diffusion norm is established under certain regularity assumptions. Finally, through numerical experiments, we verified the theoretical results.
convergent rate in a discrete streamline-diffusion norm is established under certain regularity assumptions. Finally, through numerical experiments, we verified the theoretical results.