1 results
Dispersion of particle systems in Brownian flows
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 53-74
- Print publication:
- March 1996
-
- Article
- Export citation
-
We study the dispersion of a collection of particles carried by an isotropic Brownian flow in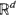
Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as t → ∞. In particular, for incompressible flows in two dimensions, we show that the variance of the center of mass grows sublinearly, while dispersion relative to the center of mass grows linearly.
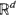Of particular interest are the center of mass and the centered spatial second moments. Their asymptotic behavior depends strongly on the spatial dimension and the largest Lyapunov exponent of the flow. We use estimates for the pair separation process to give a fairly complete picture of this behavior as 