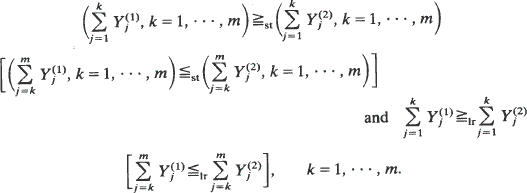1 results
Stochastic majorization of random variables by proportional equilibrium rates
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 854-872
- Print publication:
- December 1987
-
- Article
- Export citation
-
The equilibrium rate rY of a random variable Y with support on non-negative integers is defined by rY(0) = 0 and rY(n) = P[Y = n – 1]/P[Y – n],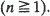
Let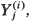 
(j = 1, …, m; i = 1,2) be 2m independent random variables that have proportional equilibrium rates with 
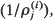(j = 1, …, m; i = 1, 2) as the constant of proportionality. When the equilibrium rate is increasing and concave [convex] it is shown that 
, …, 
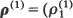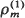) majorizes 
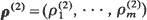implies 
, …, 
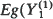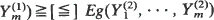for all increasing Schur-convex [concave] functions 
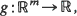whenever the expectations exist. In addition if 
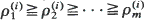, (i = 1, 2), then
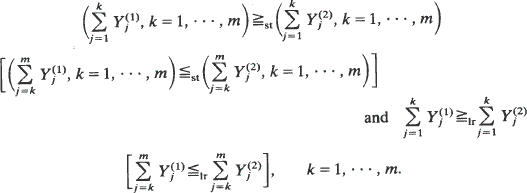
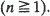Let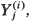 
(
(
, …, 
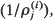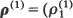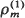) majorizes 
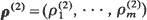implies 
, …, 
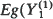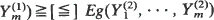for all increasing Schur-convex [concave] functions 
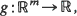whenever the expectations exist. In addition if 
, (
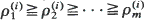