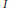1 results
Connections on a Parabolic Principal Bundle, II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 2 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-185
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
-
In Connections on a parabolic principal bundle over a curve,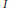
$I$ we defined connections on a parabolic principal bundle. While connections on usual principal bundles are defined as splittings of the Atiyah exact sequence, it was noted in the above article that the Atiyah exact sequence does not generalize to the parabolic principal bundles. Here we show that a twisted version of the Atiyah exact sequence generalizes to the context of parabolic principal bundles. For usual principal bundles, giving a splitting of this twisted Atiyah exact sequence is equivalent to giving a splitting of the Atiyah exact sequence. Connections on a parabolic principal bundle can be defined using the generalization of the twisted Atiyah exact sequence.
