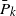The performance and effectiveness of an age replacement policy can be assessed by its mean time to failure (MTTF) function. We develop shock model theory in different scenarios for classes of life distributions based on the MTTF function where the probabilities $\bar{P}_k$ of surviving the first k shocks are assumed to have discrete DMTTF, IMTTF and IDMTTF properties. The cumulative damage model of A-Hameed and Proschan [1] is studied in this context and analogous results are established. Weak convergence and moment convergence issues within the IDMTTF class of life distributions are explored. The preservation of the IDMTTF property under some basic reliability operations is also investigated. Finally we show that the intersection of IDMRL and IDMTTF classes contains the BFR family and establish results outlining the positions of various non-monotonic ageing classes in the hierarchy.

Often in the study of reliability and its applications, the goal is to maximize or minimize certain reliability characteristics or some cost functions. For example, burn-in is a procedure used to improve the quality of products before they are used in the field. A natural question which arises is how long the burn-in procedure should last in order to maximize the mean residual life or the conditional survival probability. In the literature, an upper bound for the optimal burn-in time is obtained by assuming that the underlying distribution of the products has a bathtub-shaped failure rate function; however, no lower bound is available. A similar question arises in studying replacement policy, warranty policy, and inspection models. This article gives a lower bound for the optimal burn-in time, and lower and upper bounds for the optimal replacement and warranty policies, under the same bathtub-shape assumption.

A well-known maintenance procedure for stochastically failing units is the age replacement policy (ARP). Under the ARP a unit is replaced on failure, or when it reaches a predetermined critical age.

In previous papers concerned with this procedure the authors searched for the optimal critical age to minimize the objective function under discussion. The purpose of this paper is to prove that the ARP itself is the optimal decision rule amongst all reasonable policies.