The fractional nonhomogeneous Poisson process was introduced by a time change of the nonhomogeneous Poisson process with the inverse α-stable subordinator. We propose a similar definition for the (nonhomogeneous) fractional compound Poisson process. We give both finite-dimensional and functional limit theorems for the fractional nonhomogeneous Poisson process and the fractional compound Poisson process. The results are derived by using martingale methods, regular variation properties and Anscombe’s theorem. Eventually, some of the limit results are verified in a Monte Carlo simulation.

We consider a class of multi-type particle systems whose structure is similar to that of a contact process and show that additivity is equivalent to the existence of a dual process, extending a result of Harris. We prove a necessary and sufficient condition for the model to preserve positive correlations. We then show that complete convergence on Zd holds for a large subclass of models including the two-stage contact process and a household model, and give examples.

For any strictly positive martingale S = eX for which X has a characteristic function, we provide an expansion for the implied volatility. This expansion is explicit in the sense that it involves no integrals, but only polynomials in the log-strike. We illustrate the versatility of our expansion by computing the approximate implied volatility smile in three well-known martingale models: one finite activity exponential Lévy model, Merton (1976), one infinite activity exponential Lévy model (variance gamma), and one stochastic volatility model, Heston (1993). Finally, we illustrate how our expansion can be used to perform a model-free calibration of the empirically observed implied volatility surface.

Pareto distributions are most popular for modeling heavy tailed data. Here, we obtain weak limits of a sequence of extremal and a sequence of additive processes constructed by a series of Bernoulli point processes with bivariate Pareto space components. For the limiting processes we derive the one dimensional distributions in explicit forms. Some of the main properties of these distributions are also proved.

We study the tail behavior of regularly varying infinitely divisible random vectors and additive processes, i.e. stochastic processes with independent but not necessarily stationary increments. We show that the distribution of an infinitely divisible random vector is tail equivalent to its Lévy measure and we study the asymptotic decay of the probability for an additive process to hit sets far away from the origin. The results are extensions of known univariate results to the multivariate setting; we exemplify some of the difficulties that arise in the multivariate case.

We consider risk processes that locally behave like Brownian motion with some drift and variance, these both depending on an underlying Markov chain that is also used to generate the claims arrival process. Thus, claims arrive according to a renewal process with waiting times of phase type. Positive claims (downward jumps) are always possible but negative claims (upward jumps) are also allowed. The claims are assumed to form an independent, identically distributed sequence, independent of everything else. As main results, the joint Laplace transform of the time to ruin and the undershoot at ruin, as well as the probability of ruin, are explicitly determined under the assumption that the Laplace transform of the positive claims is a rational function. Both the joint Laplace transform and the ruin probability are decomposed according to the type of ruin: ruin by jump or ruin by continuity. The methods used involve finding certain martingales by first finding partial eigenfunctions for the generator of the Markov process composed of the risk process and the underlying Markov chain. We also use certain results from complex function theory as important tools.

We consider the variation in size of raw silk in the fixed size raw silk reeling process, and the relations between occurrences of feeding ends and some properties of cocoons from the stochastic viewpoint. The results obtained by stochastic analysis appear reasonable for the reeling experiment using three groups of cocoons.

Conditions are derived under which a probability measure on the Borel subsets of [0, ∞) is a stationary distribution for the content {Xt} of an infinite dam whose cumulative input {At} is a pure-jump Lévy process and whose release rate is a non-decreasing continuous function r(·) of the content. The conditions are used to find stationary distributions in a number of special cases, in particular when 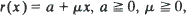and when r(x) = xα and {At} is stable with index β ∊ (0, 1). In general if EAt, < ∞ and r(0 +) > 0 it is shown that the condition sup r(x)>EA1 is necessary and sufficient for a stationary distribution to exist, a stationary distribution being found explicitly when the conditions are satisfied. If sup r(x)>EA1 it is shown that there is at most one stationary distribution and that if there is one then it is the limiting distribution of {Xt} as t → ∞. For {At} stable with index β and r(x) = xα, α + β = 1, we show also that 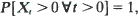complementing results of Brockwell and Chung for the zero-set of {Xt} in the cases α + β < 1 and α + β > 1. We conclude with a brief treatment of the finite dam, regarded as a limiting case of infinite dams with suitably chosen release functions.

A class of probability models for the firing of neurons is introduced and treated analytically. The cell membrane potential is assumed to be a one-dimensional random walk on the continuum; the first passage of the moving boundary triggers a nerve spike, an all-or-none event. The interspike interval distribution of first-passage time is shown to satisfy a Volterra integral equation suitable for numerical evaluation. Explicit solutions as well as their Laplace (Mellin) transforms are obtained for some special cases. The main technique used in this paper is the extension of Wald's fundamental identity of sequential analysis to a wide range of additive stochastic processes with an (eventually) linear boundary function. This identity is also useful in evaluating model parameters in terms of observed firing times, as well as providing a unified exposition of many earlier results.