1 results
Adaptive simulation using perfect control variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 859-876
- Print publication:
- September 2004
-
- Article
- Export citation
-
We introduce adaptive-simulation schemes for estimating performance measures for stochastic systems based on the method of control variates. We consider several possible methods for adaptively tuning the control-variate estimators, and describe their asymptotic properties. Under certain assumptions, including the existence of a ‘perfect control variate’, all of the estimators considered converge faster than the canonical rate of n −1/2, where n is the simulation run length. Perfect control variates for a variety of stochastic processes can be constructed from ‘approximating martingales’. We prove a central limit theorem for an adaptive estimator that converges at rate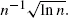
A similar estimator converges at rate n
−1. An exponential rate of convergence is also possible under suitable conditions.
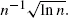A similar estimator converges at rate 