Let n be a positive integer and $\underline {n}=\{1,2,\ldots ,n\}$. A conjecture arising from certain polynomial near-ring codes states that if $k\geq 1$ and $a_{1},a_{2},\ldots ,a_{k}$ are distinct positive integers, then the symmetric difference $a_{1}\underline {n}\mathbin {\Delta }a_{2}\underline {n}\mathbin {\Delta }\cdots \mathbin {\Delta }a_{k}\underline {n}$ contains at least n elements. Here, $a_{i}\underline {n}=\{a_{i},2a_{i},\ldots ,na_{i}\}$ for each i. We prove this conjecture for arbitrary n and for $k=1,2,3$.

Brizolis asked for which primes p greater than 3 there exists a pair (g,h) such that h is a fixed point of the discrete exponential map with base g, or equivalently h is a fixed point of the discrete logarithm with base g. Various authors have contributed to the understanding of this problem. In this paper, we use p-adic methods, primarily Hensel’s lemma and p-adic interpolation, to count fixed points, two-cycles, collisions, and solutions to related equations modulo powers of a prime p.

For a given elliptic curve 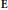$\mathbf{E}$, we obtain an upper bound on the discrepancy of sets of multiples 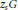${{z}_{s}}G$ where ${{z}_{s}}$ runs through a sequence 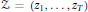$Z\,=\,\left( {{z}_{1}},\ldots ,{{z}_{T}} \right)$ such that 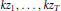$k{{z}_{1}},\ldots ,k{{z}_{T}}$ is a permutation of 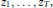${{z}_{1}},\ldots ,{{z}_{T}}$, both sequences taken modulo $t$, for sufficiently many distinct values of $k$ modulo $t$.

We apply this result to studying an analogue of the power generator over an elliptic curve. These results are elliptic curve analogues of those obtained for multiplicative groups of finite fields and residue rings.