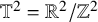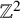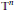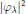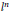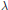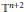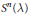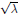We consider momentum push-forwards of measures arising as quantum limits (semiclassical measures) of eigenfunctions of a point scatterer on the standard flat torus
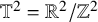 ${\mathbb T}^2 = {\mathbb R}^2/{\mathbb Z}^{2}$
. Given any probability measure arising by placing delta masses, with equal weights, on
${\mathbb T}^2 = {\mathbb R}^2/{\mathbb Z}^{2}$
. Given any probability measure arising by placing delta masses, with equal weights, on
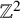 ${\mathbb Z}^2$
-lattice points on circles and projecting to the unit circle, we show that the mass of certain subsequences of eigenfunctions, in momentum space, completely localizes on that measure and are completely delocalized in position (i.e., concentration on Lagrangian states). We also show that the mass, in momentum, can fully localize on more exotic measures, for example, singular continuous ones with support on Cantor sets. Further, we can give examples of quantum limits that are certain convex combinations of such measures, in particular showing that the set of quantum limits is richer than the ones arising only from weak limits of lattice points on circles. The proofs exploit features of the half-dimensional sieve and behavior of multiplicative functions in short intervals, enabling precise control of the location of perturbed eigenvalues.
${\mathbb Z}^2$
-lattice points on circles and projecting to the unit circle, we show that the mass of certain subsequences of eigenfunctions, in momentum space, completely localizes on that measure and are completely delocalized in position (i.e., concentration on Lagrangian states). We also show that the mass, in momentum, can fully localize on more exotic measures, for example, singular continuous ones with support on Cantor sets. Further, we can give examples of quantum limits that are certain convex combinations of such measures, in particular showing that the set of quantum limits is richer than the ones arising only from weak limits of lattice points on circles. The proofs exploit features of the half-dimensional sieve and behavior of multiplicative functions in short intervals, enabling precise control of the location of perturbed eigenvalues.