Invariant submanifolds of contact (κ, μ)-manifolds are studied. Our main result is that any invariant submanifold of a non-Sasakian contact (κ, μ)-manifold is always totally geodesic and, conversely, every totally geodesic submanifold of a non-Sasakian contact (κ, μ)-manifold, μ ≠ 0, such that the characteristic vector field is tangent to the submanifold is invariant. Some consequences of these results are then discussed.
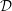 ${\mathcal{D}}$-Einstein Real Hypersurfaces in
${\mathcal{D}}$-Einstein Real Hypersurfaces in 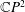 $\mathbb{C}P^{2}$ and
$\mathbb{C}P^{2}$ and 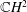 $\mathbb{C}H^{2}$
$\mathbb{C}H^{2}$