1 results
Consistency of Moment Systems
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 5 / 01 October 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 995-1006
- Print publication:
- 01 October 1995
-
- Article
-
- You have access
- Export citation
-
An important question in the study of moment problems is to determine when a fixed point in ℝn lies in the moment cone of vectors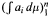
, with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.
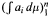, with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.