Let t be a sequence in (0,1) that converges to 0, and define the Abel matrix At by ank = tn(1-tn)k. The matrix At determines a sequence-to-sequence variant of the classical Abel summability method. The purpose of this paper is to study these transformations as l-l summability methods: e.g., At maps l1 into l1 if and only if t is in l1. The Abel matrices are shown to be stronger l-l methods than the Euler-Knopp means and the Nӧrlund means. Indeed, if t is in l1 and Σ xk has bounded partial sums, then Atx is in l1. Also, the Abel matrix is shown to be translative in an l-l sense, and an l-l Tauberian theorem is proved for At.

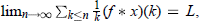 then
then 