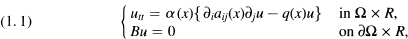1 results
Scattering Theory And Spectral Representations For General Wave Equations With Short Range Perturbations
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 2 / 01 April 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 435-448
- Print publication:
- 01 April 1991
-
- Article
-
- You have access
- Export citation
-
In this paper we shall develop the scattering theory introduced by Lax and Phillips [5] for the following general wave equation;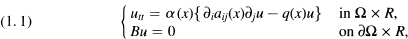
where Ω is an exterior domain Rn(n ≥ 3) with the smooth boundary δΩ and B is either a Dirichlet boundary condition or of the form Bu = Vi(x)aij(x)δju+σ(x)u with the unit outer normal vector v(x) = (v1 , … , vn) at x ∈ δ Ω. The precise assumptions on α(x), aij(x),q(x), σ(x) are denoted below. If Ω is an inhomogeneous medium with the density ρ (x), the propagation of waves is described by (1.1) with a(x) = a(x)2 ρ(x), aij(x) = ρ-l(x) δij and q(x) = 0 with the velocity a(x).
