The degenerate Cahn–Hilliard equation is a standard model to describe living tissues. It takes into account cell populations undergoing short-range attraction and long-range repulsion effects. In this framework, we consider the usual Cahn–Hilliard equation with a singular single-well potential and degenerate mobility. These degeneracy and singularity induce numerous difficulties, in particular for its numerical simulation. To overcome these issues, we propose a relaxation system formed of two second-order equations which can be solved with standard packages. This system is endowed with an energy and an entropy structure compatible with the limiting equation. Here, we study the theoretical properties of this system: global existence and convergence of the relaxed system to the degenerate Cahn–Hilliard equation. We also study the long-time asymptotics which interest relies on the numerous possible steady states with given mass.

We study the steady states and dynamics of a thin-film-type equation with non-conserved mass in one dimension. The evolution equation is a non-linear fourth-order degenerate parabolic partial differential equation (PDE) motivated by a model of volatile viscous fluid films allowing for condensation or evaporation. We show that by changing the sign of the non-conserved flux and breaking from a gradient flow structure, the problem can exhibit novel behaviours including having two distinct classes of co-existing steady-state solutions. Detailed analysis of the bifurcation structure for these steady states and their stability reveals several possibilities for the dynamics. For some parameter regimes, solutions can lead to finite-time rupture singularities. Interestingly, we also show that a finite-amplitude limit cycle can occur as a singular perturbation in the nearly conserved limit.

Let Ω be a smooth bounded domain in RN, with N ≥ 5. We provide existence and bifurcation results for the elliptic fourth-order equation Δ2u − Δpu = f(λ, x, u) in Ω, under the Dirichlet boundary conditions u = 0 and ∇u = 0. Here λ is a positive real number, 1 < p ≤ 2# and f(.,., u) has a subcritical or a critical growth s, 1 < s ≤ 2*, where 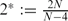and 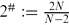. Our approach is variational, and it is based on the mountain-pass theorem, the Ekeland variational principle and the concentration-compactness principle.