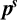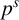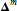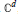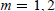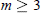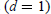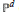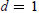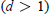We prove general Dwork-type congruences for constant terms attached to tuples of Laurent polynomials. We apply this result to establishing arithmetic and p-adic analytic properties of functions originating from polynomial solutions modulo $p^s$ of hypergeometric and Knizhnik–Zamolodchikov (KZ) equations, solutions which come as coefficients of master polynomials and whose coefficients are integers. As an application, we show that the simplest example of a p-adic KZ connection has an invariant line subbundle while its complex analog has no nontrivial subbundles due to the irreducibility of its monodromy representation.

We introduce a family of orthogonal functions, termed as generalized Slepian functions (GSFs), closely related to the time-frequency concentration problem on a unit disk in D. Slepian [19]. These functions form a complete orthogonal system in with , and can be viewed as a generalization of the Jacobi polynomials with parameter (α, 0). We present various analytic and asymptotic properties of GSFs, and study spectral approximations by such functions.

A simple integral formula as an iterated residue is presented for the Baker–Akhiezer function related to An-type root system in both the rational and trigonometric cases. We present also a formula for the Baker–Akhiezer function as a Selberg-type integral and generalise it to the deformed An,1-case. These formulas can be interpreted as new cases of explicit evaluation of Selberg-type integrals.

The aim of the present paper is the computation of Green's functions for the powers 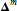${{\mathbf{\Delta }}^{m}}$ of the invariant Laplace operator on rank-one Hermitian symmetric spaces. Starting with the noncompact case, the unit ball in 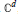${{\mathbb{C}}^{d}}$, we obtain a complete result for 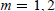$m\,=\,1,\,2$ in all dimensions. For 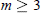$m\,\ge \,3$ the formulas grow quite complicated so we restrict ourselves to the case of the unit disc 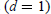$(d\,=\,1)$ where we develop a method, possibly applicable also in other situations, for reducing the number of integrations by half, and use it to give a description of the boundary behaviour of these Green functions and to obtain their (multi-valued) analytic continuation to the entire complex plane. Next we discuss the type of special functions that turn up (hyperlogarithms of Kummer). Finally we treat also the compact case of the complex projective space 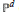${{\mathbb{P}}^{d}}$ (for 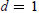$d\,=\,1$, the Riemann sphere) and, as an application of our results, use eigenfunction expansions to obtain some new identities involving sums of Legendre 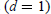$(d\,=\,1)$ or Jacobi 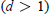$(d\,>\,1)$ polynomials and the polylogarithm function. The case of Green's functions of powers of weighted (no longer invariant, but only covariant) Laplacians is also briefly discussed.