Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • Modification of balayage spaces by transitions with application to coupling of PDE’s

  • Wolfhard Hansen
  • Journal:
    Nagoya Mathematical Journal / Volume 169 / 2003
    Published online by Cambridge University Press:
    22 January 2016, pp. 77-118
    Print publication:
    2003
    • Article
      • You have access
    • PDF
    • Export citation

  • Modifications of balayage spaces are studied which, in probabilistic terms, correspond to killing and transitions (creation of mass combined with jumps). This is achieved by a modification of harmonic kernels for sufficiently small open sets. Applications to coupling of elliptic and parabolic partial differential equations of second order are discussed.

  • A Decomposition Theorem for Positive Superharmonic Functions

  • Sirkka-Liisa Eriksson-Bique
  • Journal:
    Canadian Mathematical Bulletin / Volume 33 / Issue 3 / 01 September 1990
    Published online by Cambridge University Press:
    20 November 2018, pp. 286-296
    Print publication:
    01 September 1990
    • Article
      • You have access
    • PDF
    • Export citation

  • Let X be a harmonic space in the sense of C. Constantinescu and A. Cornea. We show that, for any subset E of X, a positive superharmonic function u on X has a representation u = p + h, where p is the greatest specific minorant of u satisfying 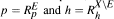. This result is a generalization of a theorem of M. Brelot. We also state some characterizations of extremal superharmonic functions.