We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In a group, a nonidentity element is called a generalized torsion element if some product of its conjugates equals the identity. We show that for many classical knots one can ûnd generalized torsion in the fundamental group of its complement, commonly called the knot group. It follows that such a group is not bi-orderable. Examples include all torus knots, the (hyperbolic) knot
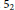${{5}_{2}}$
, and algebraic knots in the sense of Milnor.
