We show how some Ulam stability issues can be approached for functions taking values in 2-Banach spaces. We use the example of the well-known Cauchy equation 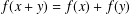 $f(x+y)=f(x)+f(y)$, but we believe that this method can be applied for many other equations. In particular we provide an extension of an earlier stability result that has been motivated by a problem of Th. M. Rassias. The main tool is a recent fixed point theorem in some spaces of functions with values in 2-Banach spaces.
$f(x+y)=f(x)+f(y)$, but we believe that this method can be applied for many other equations. In particular we provide an extension of an earlier stability result that has been motivated by a problem of Th. M. Rassias. The main tool is a recent fixed point theorem in some spaces of functions with values in 2-Banach spaces.