In 2012, Blecher [‘Geometry for totally symmetric plane partitions (TSPPs) with self-conjugate main diagonal’, Util. Math. 88 (2012), 223–235] introduced a special class of totally symmetric plane partitions, called 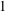 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1$-shell totally symmetric plane partitions. Let
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1$-shell totally symmetric plane partitions. Let 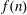 $f(n)$ denote the number of
$f(n)$ denote the number of 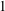 $1$-shell totally symmetric plane partitions of weight
$1$-shell totally symmetric plane partitions of weight  $n$. More recently, Hirschhorn and Sellers [‘Arithmetic properties of 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc. to appear. Published online 27 September 2013] discovered a number of arithmetic properties satisfied by
$n$. More recently, Hirschhorn and Sellers [‘Arithmetic properties of 1-shell totally symmetric plane partitions’, Bull. Aust. Math. Soc. to appear. Published online 27 September 2013] discovered a number of arithmetic properties satisfied by 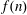 $f(n)$. In this paper, employing some results due to Cui and Gu [‘Arithmetic properties of
$f(n)$. In this paper, employing some results due to Cui and Gu [‘Arithmetic properties of 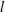 $l$-regular partitions’, Adv. Appl. Math. 51 (2013), 507–523], and Hirschhorn and Sellers, we prove several new infinite families of congruences modulo 4 and 8 for
$l$-regular partitions’, Adv. Appl. Math. 51 (2013), 507–523], and Hirschhorn and Sellers, we prove several new infinite families of congruences modulo 4 and 8 for 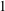 $1$-shell totally symmetric plane partitions. For example, we find that, for
$1$-shell totally symmetric plane partitions. For example, we find that, for 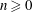 $n\geq 0$ and
$n\geq 0$ and 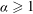 $\alpha \geq 1$,
$\alpha \geq 1$, 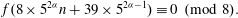 $$\begin{equation*} f(8 \times 5^{2\alpha } n+39\times 5^{2\alpha -1})\equiv 0 \pmod 8. \end{equation*}$$
$$\begin{equation*} f(8 \times 5^{2\alpha } n+39\times 5^{2\alpha -1})\equiv 0 \pmod 8. \end{equation*}$$