Finite localities I

Introduction

This is the first of a series of papers concerning what might be thought of as ‘locally grouped spaces’, in a loose analogy with the locally ringed spaces of algebraic geometry. The spaces that we have in mind are simplicial sets that generalise the simplicial sets that underlie and determine the classifying spaces of finite (or compact) groups. If the analogy is pursued, then the role of ‘structure sheaf’ is provided by the ‘fusion systems’ associated with these spaces. Our approach here will be purely algebraic and combinatorial, so we will not be concerned with topological realisations. All of the groups to be considered will be finite; but a parallel series of papers representing some joint work with Alex Gonzalez will considerably broaden the scope.

Finite localities were introduced by the author in [Ch1], in order to give a positive solution to this question: Given a saturated fusion system $\mathcal {F}$ on a finite p-group, does there exist a ‘classifying space’ for $\mathcal {F}$ , and if so, is such a space unique up to isomorphism? The solution given in [Ch1] was closely tied to the specific goal and did not allow for a complete development of ideas. The aim here is to provide such a development. In part, our aim is to supplement the theory of saturated fusion systems over a finite p-group. As part of that program, we shall need to establish a sort of dictionary that will establish an equivalence between such notions as ‘partial normal subgroup of a proper locality’ and ‘normal subsystem of a saturated fusion system’. This is done in a separate paper coauthored with Ellen Henke [ChHe].

The division into several papers closely parallels the extent to which fusion systems are drawn into the developing picture. This Part I can be characterised by its having no direct involvement with fusion systems, and by there being no mention in it of $p'$ -elements or $p'$ -subgroups of a group, other than in one application (see Proposition 4.12).

Let G be a group, and let $\mathbf {W}(G)$ be the free monoid on G. Thus, $\mathbf {W}(G)$ is the set of all words in the alphabet G, with the binary operation given by concatenation of words. The product $G\times G\to G$ extends, by generalised associativity, to a ‘product’ $\Pi :\mathbf {W}(G)\to G$ , whereby a word $w=(g_1,\cdots ,g_n)\in \mathbf {W}(G)$ is mapped to $g_1\cdots g_n$ . The inversion map on G induces an ‘inversion’ on $\mathbf {W}(G)$ , sending w to $(g_n^{-1},\cdots ,g_1^{-1})$ . In fact, one may easily replace the standard definition of ‘group’ by a definition given in terms of $\Pi $ and the inversion on $\mathbf {W}(G)$ . One obtains the notion of partial group by restricting the domain of $\Pi $ to a subset $\mathbf {D}$ of $\mathbf {W}(G)$ , where $\mathbf {D}$ , the product, and the inversion, are required to satisfy conditions (see Definition 1.1) that preserve the outlines of the strictly group-theoretic setup. When one looks at things in this way, a group is simply a partial group G having the property that $\mathbf {D}=\mathbf {W}(G)$ .

The notions of partial subgroup and homomorphism of partial groups immediately suggest themselves, and a partial subgroup of a partial group $\mathcal {L}$ may in fact be a group. We say that the partial group $\mathcal {L}$ is ‘objective’ (see Definition 2.1) provided that the domain $\mathbf {D}$ of the product is determined in a certain way by a collection $\Delta $ of subgroups of $\mathcal {L}$ (the set of ‘objects’), and provided that $\Delta $ has a certain ‘closure’ property. If also $\mathcal {L}$ is finite and there exists $S\in \Delta $ such that $\Delta $ is a collection of subgroups of S, where S is maximal in the set (partially ordered by inclusion) of p-subgroups of $\mathcal {L}$ , then $(\mathcal {L},\Delta ,S)$ is a (finite) locality.

The basic properties of partial groups, objective partial groups and localities will be derived in Sections 1 and 2. We then begin in Section 3 to consider partial normal subgroups of localities in detail. One of the two key results in Section 3 is the Frattini lemma (Corollary 3.11), which states that if $\mathcal {N}\trianglelefteq \mathcal {L}$ is a partial normal subgroup, then $\mathcal {L}=N_{\mathcal {L}}(S\cap \mathcal {N})\mathcal {N}$ . The other is Stellmacher’s splitting lemma (Lemma 3.12), which leads to the partition of $\mathcal {L}$ into a collection of ‘maximal cosets’ of $\mathcal {N}$ and to a partial group structure on the set $\mathcal {L}/\mathcal {N}$ of maximal cosets. In Section 4, it is shown that $\mathcal {L}/\mathcal {N}$ is in fact a locality, and we obtain versions of the first Nóther isomorphism theorem and its familiar consequences. In particular, the notions ‘partial normal subgroup’ and ‘kernel of a projection’ turn out to be equivalent. This may be compared with the situation in the theory of saturated fusion systems, where it is known that no such equivalence exists.

Section 5 concerns products of partial normal subgroups. The main result here (Theorem 5.1) has since been considerably strengthened by Henke [He], who shows that the product of any two partial normal subgroups of a locality is again a partial normal subgroup. The paper ends with a result (Proposition 5.5) that provides an application of essentially all of the concepts and results from all of the earlier sections and will play a role in Part III.

Composition of mappings will most often be written from left to right, and mappings that are likely to be composed with others will be written to the right of their arguments. In particular, this entails that conjugation within a group G be taken in the right-handed sense, which is standard in finite group theory; so that $x^g=g^{-1} xg$ for any $x,g\in G$ .

1 Partial groups

The reader is asked to forget what a group is and to trust that what was forgotten will soon be recovered.

For any set X, write $\mathbf {W}(X)$ for the free monoid on X. Thus, an element of $\mathbf {W}(X)$ is a finite sequence of (or word in) the elements of X, and the multiplication in $\mathbf {W}(X)$ consists of concatenation of words, to be denoted $u\circ v$ . The length of the word $(x_1,\cdots ,x_n)$ is n. The empty word is the word $(\emptyset )$ of length 0. We make no distinction between X and the set of words of length $1$ .

Definition 1.1. Let $\mathcal {L}$ be a nonempty set, let $\mathbf {W}=\mathbf {W}(\mathcal {L})$ be the free monoid on $\mathcal {L}$ , and let $\mathbf {D}$ be a subset of $\mathbf {W}$ such that

1. (1) $\mathcal {L}\subseteq \mathbf {D}$ (that is, $\mathbf {D}$ contains all words of length 1), and

   $$ \begin{align*} u\circ v\in\mathbf{D}\implies u,v\in\mathbf{D}. \end{align*} $$

Notice that since $\mathcal {L}$ is nonempty, (1) implies that also the empty word is in $\mathbf {D}$ .

A mapping $\Pi :\mathbf {D}\to \mathcal {L}$ is a product if

1. (2) $\Pi $ restricts to the identity map on $\mathcal {L}$ , and

2. (3) $u\circ v\circ w\in \mathbf {D}\implies u\circ \Pi (v)\circ w\in \mathbf {D}$ , and $\Pi (u\circ v\circ w)=\Pi (u\circ \Pi (v)\circ w)$ .

An inversion on $\mathcal {L}$ consists of an involutory bijection $x\mapsto x^{-1}$ on $\mathcal {L}$ , together with the mapping $w\mapsto w^{-1}$ on $\mathbf {W}$ given by

$$ \begin{align*} (x_1,\cdots,x_n)\mapsto(x_n^{-1},\cdots x_1^{-1}). \end{align*} $$

We say that $\mathcal {L}$ , with the product $\Pi :\mathbf {D}\to \mathcal {L}$ and inversion $(-)^{-1}$ , is a partial group if

1. (4) $w\in \mathbf {D}\implies w^{-1}\circ w\in \mathbf {D}$ and $\Pi (w^{-1}\circ w)=\mathbf {1}$ ,

where $\mathbf {1}$ denotes the image of the empty word under $\Pi $ . Notice that (1) and (4) yield $w^{-1}\in \mathbf {D}$ if $w\in \mathbf {D}$ . As $(w^{-1})^{-1}=w$ , condition (4) is symmetric.

Example 1.2. Let $\mathcal {L}$ be the $3$ -element set $\{\mathbf {1},a,b\}$ , and let $\mathbf {D}$ be the subset of $\mathbf {W}(\mathcal {L})$ consisting of all words w such that the word obtained from w by deleting all entries equal to $\mathbf {1}$ is an alternating string of as and bs (of odd or even length and that, if nonempty, may begin either with a or with b). Define $\Pi :\mathbf {D}\to \mathcal {L}$ by the formula $\Pi (w)=\mathbf {1}$ if the number of a-entries in w is equal to the number of bs; $\Pi (w)=a$ if the number of as exceeds the number of bs (necessarily by 1); and $\Pi (w)=b$ if the number of bs exceeds the number of as. Define inversion on $\mathcal {L}$ by $\mathbf {1}^{-1}=\mathbf {1}$ , $a^{-1}=b$ and $b^{-1}=a$ . It is then easy to check that $\mathcal {L}$ , with these structures, is a partial group. In fact, $\mathcal {L}$ is the ‘free partial group on one generator’, as will be made clear in Example 1.12 below.

It will be convenient to make this definition: a group is a partial group $\mathcal {L}$ in which $\mathbf {W}(\mathcal {L})=\mathbf {D}$ . To distinguish between this definition and the usual one, we shall use the expression ‘binary group’ for a nonempty set G with an associative binary operation, identity element and inverses in the usual sense. The following lemma shows that the distinction is subtle.

Lemma 1.3.

1. (a) Let G be a binary group, and let $\Pi :\mathbf {W}(G)\to G$ be the ‘multivariable product’ on G given by $(g_1,\cdots ,g_n)\mapsto g_1\cdots g_n$ . Then G, together with $\Pi $ and the inversion in G, is a partial group, with $\mathbf {D}=\mathbf {W}(G)$ .

2. (b) Let $\mathcal {L}$ be a group: that is, a partial group for which $\mathbf {W}(\mathcal {L})=\mathbf {D}$ . Then $\mathcal {L}$ is a binary group with respect to the operation given by restricting $\Pi $ to words of length 2 and with respect to the inversion in $\mathcal {L}$ . Moreover, $\Pi $ is then the multivariable product on $\mathcal {L}$ defined as in (a).

Proof. Point (a) is given by generalised associativity in the binary group G. Point (b) is a straightforward exercise and is left to the reader.

Here are a few basic consequences of Definition 1.1.

Lemma 1.4. Let $\mathcal {L}$ (with $\mathbf {D}$ , $\Pi $ , and the inversion) be a partial group.

1. (a) $\Pi $ is $\mathbf {D}$ -multiplicative. That is, if $u\circ v$ is in $\mathbf {D}$ , then the word $(\Pi (u),\Pi (v))$ of length 2 is in $\mathbf {D}$ , and

   $$ \begin{align*}\Pi(u\circ v)=\Pi(u)\Pi(v), \end{align*} $$
   where ‘ $\Pi (u)\Pi (v)$ ’ is an abbreviation for $\Pi ((\Pi (u),\Pi (v))$ .

2. (b) $\Pi $ is $\mathbf {D}$ -associative. That is,

   $$ \begin{align*} u\circ v\circ w\in\mathbf{D}\implies\Pi(u\circ v)\Pi(w)=\Pi(u)\Pi(v\circ w). \end{align*} $$

3. (c) We have $u\circ v\in \mathbf {D}$ if and only if $u\circ (\mathbf {1})\circ v\in \mathbf {D}$ , and then $=\Pi (u\circ v)=\Pi (u\circ (\mathbf {1})\circ v)$ .

4. (d) If $u\circ v\in \mathbf {D}$ , then both $u^{-1}\circ u\circ v$ and $u\circ v\circ v^{-1}$ are in $\mathbf {D}$ , $\Pi (u^{-1}\circ u\circ v)=\Pi (v)$ and $\Pi (u\circ v\circ v^{-1})=\Pi (u)$ .

5. (e) The cancellation rule: If both $u\circ v$ and $u\circ w$ are in $\mathbf {D}$ , and $\Pi (u\circ v)=\Pi (u\circ w)$ , then $\Pi (v)=\Pi (w)$ (and similarly for right cancellation).

6. (f) If $u\in \mathbf {D}$ , then $u^{-1}\in \mathbf {D}$ , and $\Pi (u^{-1})=\Pi (u)^{-1}$ . In particular, $\mathbf {1}^{-1}=\mathbf {1}$ .

7. (g) The uncancellation rule: Suppose that both $u\circ v$ and $u\circ w$ are in $\mathbf {D}$ and that $\Pi (v)=\Pi (w)$ . Then $\Pi (u\circ v)=\Pi (u\circ w)$ . $($ Similarly for right uncancellation. $)$

Proof. Let $u\circ v\in \mathbf {D}$ . Then Definition 1.1(3) applies to $(\emptyset )\circ u\circ v$ and yields $(\Pi (u))\circ v\in \mathbf {D}$ with $\Pi (u\circ v)=\Pi ((\Pi (u))\circ v)$ . Now apply Definition 1.1(3) to $(\Pi (u))\circ v\circ (\emptyset )$ to obtain (a).

Let $u\circ v\circ w\in \mathbf {D}$ . Then $u\circ v$ and w are in $\mathbf {D}$ by Definition 1.1(1), and $\mathbf {D}$ -multiplicativity yields $\Pi (u\circ v\circ w)=\Pi (u\circ v)\Pi (w)$ . Similarly, $\Pi (u\circ v\circ w)=\Pi (u)\Pi (v\circ w)$ , and (b) holds.

Since $\mathbf {1}=\Pi (\emptyset )$ , it is immediate from Definition 1.1(3) that if $w=u\circ v\in \mathbf {D}$ , then $w'=u\circ (\mathbf {1})\circ v\in \mathbf {D}$ . On the other hand, suppose that $w'\in \mathbf {D}$ . If u and v are empty, then $w=(\emptyset )\in \mathbf {D}$ . Suppose u is not the empty word, and write $u=u_0\circ (x)$ . Then $w'=u_0\circ (x,\mathbf {1})\circ v$ , and since $\Pi (x,\mathbf {1})=x$ , we obtain $w\in \mathbf {D}$ via $\mathbf {D}$ -associativity. Similarly, $w\in \mathbf {D}$ if v is nonempty, so (c) holds.

Let $u\circ v\in \mathbf {D}$ . Then $v^{-1}\circ u^{-1}\circ u\circ v\in \mathbf {D}$ by Definition 1.1(4), and then $u^{-1}\circ u\circ v\in \mathbf {D}$ by Definition 1.1(1). Multiplicativity then yields

$$ \begin{align*} \Pi(u^{-1}\circ u\circ v)=\Pi(u^{-1}\circ u)\Pi(v)=\mathbf{1}\Pi(v)= \Pi(\emptyset)\Pi(v)=\Pi(\emptyset\circ v)=\Pi(v). \end{align*} $$

As $(w^{-1})^{-1}=w$ for any $w\in \mathbf {W}$ , one obtains $w\circ w^{-1}\in \mathbf {D}$ for any $w\in \mathbf {D}$ , and $\Pi (w\circ w^{-1})=\mathbf {1}$ . From this one easily completes the proof of (d).

Now let $u\circ v$ and $u\circ w$ be in $\mathbf {D}$ , with $\Pi (u\circ v)=\Pi (u\circ w)$ . Then (d) (together with multiplicativity and associativity, which will not be explicitly mentioned hereafter) yield

$$ \begin{align*}\Pi(v)=\Pi(u^{-1}\circ u\circ v)=\Pi(u^{-1})\Pi(u)\Pi(v)=\Pi(u^{-1})\Pi(u)\Pi(w)= \Pi(u^{-1}\circ u\circ w)=\Pi(w), \end{align*} $$

and (e) holds.

Let $u\in \mathbf {D}$ . Then $u\circ u^{-1}\in \mathbf {D}$ , and then $\Pi (u)\Pi (u^{-1})=\mathbf {1}$ . But also $(\Pi (u),\Pi (u)^{-1})\in \mathbf {D}$ , and $\Pi (u)\Pi (u)^{-1}=\mathbf {1}$ . Now (f) follows by Definition 1.1(2) and cancellation.

Let $u,v,w$ be as in (g). Then $u^{-1}\circ u\circ v$ and $u^{-1}\circ u\circ w$ are in $\mathbf {D}$ by (d). By two applications of (d), $\Pi (u^{-1}\circ u\circ v)=\Pi (v)=\Pi (w)=\Pi (u^{-1}\circ u\circ w)$ , so $\Pi (u\circ v)=\Pi (u\circ w)$ by (e), and (g) holds.

It will often be convenient to eliminate the symbol ‘ $\Pi $ ’ and speak of ‘the product $g_1\cdots g_n$ ’ instead of $\Pi (g_1,\cdots ,g_n)$ . More generally, if $\{X_i\}_{1\leq i\leq n}$ is a collection of subsets of $\mathcal {L}$ , then the ‘product set $X_1\cdots X_n$ ’ is by definition the image under $\Pi $ of the set of words $(g_1,\cdots ,g_n)\in \mathbf {D}$ such that $g_i\in X_i$ for all i. If $X_i=\{g_i\}$ is a singleton, then we may write $g_i$ in place of $X_i$ in such a product. Thus, for example, the product $g^{-1} Xg$ stands for the set of all $\Pi (g^{-1},x,g)$ with $(g^{-1},x,g)\in \mathbf {D}$ , and with $x\in X$ .

A word of urgent warning: In writing products in the above way, one may be drawn into imagining that associativity holds in a stronger sense than that given by Lemma 1.4(b). This is an error that is to be avoided. For example, one should not suppose that if $(f,g,h)\in \mathbf {W}$ and both $(f,g)$ and $(fg,h)$ are in $\mathbf {D}$ , then $(f,g,h)$ is in $\mathbf {D}$ . That is, ‘the product $fgh$ ’ may be undefined even though the product $(fg)h$ is defined. Of course, one is tempted to simply extend the domain $\mathbf {D}$ to include such triples $(f,g,h)$ and ‘define’ the product $fgh$ to be $(fg)h$ . The trouble is that it may also be the case that $gh$ and $f(gh)$ are defined but $(fg)h\neq f(gh)$ .

For $\mathcal {L}$ a partial group and $g\in \mathcal {L}$ , write $\mathbf {D}(g)$ for the set of all $x\in \mathcal {L}$ such that the product $g^{-1} xg$ is defined. There is then a mapping

$$ \begin{align*} c_g:\mathbf{D}(g)\to\mathcal{L} \end{align*} $$

given by $x\mapsto g^{-1} xg$ (and called conjugation by g). Our preference is for right-hand notation for mappings, so we write

$$ \begin{align*} x\mapsto(x)c_g\quad\text{or}\quad x\mapsto x^g \end{align*} $$

for conjugation by g.

The following result provides an illustration of the preceding notational conventions and introduces a theme that will be developed further as we pass from partial groups to objective partial groups, localities and (in Part III) regular localities.

Lemma 1.5. Let $\mathcal {L}$ be a partial group, and let $f,g\in \mathcal {L}$ .

1. (a) Suppose that the products $fg$ and $gf$ are defined and that $fg=gf$ . Suppose further that $f\in \mathbf {D}(g)$ . Then $f^g=f$ .

2. (b) Suppose that $f\in \mathbf {D}(g)$ and $f^g=f$ . Then $g\in \mathbf {D}(f)$ , $fg=gf$ and $g^f=g$ .

Proof.

1. (a) We are given $(f,g)\in \mathbf {D}$ , so $(f^{-1},f,g)\in \mathbf {D}$ and $\Pi (f^{-1},f,g)=g$ , by Lemma 1.4(d) and $\mathbf {D}$ -associativity. We are also given $f\in \mathbf {D}(g)$ and $fg=gf$ , so

   $$ \begin{align*}f^g=\Pi(g^{-1},f,g)=\Pi((g^{-1},fg)=\Pi(g^{-1},gf)=\Pi(g^{-1},g,f)=f. \end{align*} $$

2. (b) Set $v=(f^{-1},g,g^{-1},f,g)$ . As $(g^{-1},f,g)\in \mathbf {D}$ , it follows from Lemma 1.4(d) that also $v\in \mathbf {D}$ and $\Pi (v)=g$ . Then $(f^{-1},g,f)=(f^{-1},g,f^g)\in \mathbf {D}$ by $\mathbf {D}$ -associativity and $\Pi (v)=g^f=g$ . Also, from $v\in \mathbf {D}$ , we obtain $(f,g)\in \mathbf {D}$ from Definition 1.1(1), so $(g,g^{-1},f,g)\in \mathbf {D}$ by Lemma 1.4(d). Then $\mathbf {D}$ -associativity yields $fg=\Pi (g,g^{-1},f,g)=gf^g=gf$ .

Notation. From now on, in any given partial group $\mathcal {L}$ , usage of the symbol ‘ $x^g$ ’ shall be taken to imply $x\in \mathbf {D}(g)$ . More generally, for X a subset of $\mathcal {L}$ and $g\in \mathcal {L}$ , usage of ‘ $X^g$ ’ shall be taken to mean that $X\subseteq \mathbf {D}(g)$ , whereupon $X^g$ is by definition the set of all $x^g$ with $x\in X$ .

At this early point, and in the context of arbitrary partial groups, one can say very little about the maps $c_g$ . The cancellation rule in Lemma 1.4(e) implies that each $c_g$ is injective, but beyond that the following lemma may be the best that can be obtained.

Lemma 1.6. Let $\mathcal {L}$ be a partial group, and let $g\in \mathcal {L}$ . Then the following hold:

1. (a) $\mathbf {1}\in \mathbf {D}(g)$ , and ${\mathbf {1}}^g=\mathbf {1}$ .

2. (b) $\mathbf {D}(g)$ is closed under inversion, and $(x^{-1})^g=(x^g)^{-1}$ for all $x\in \mathbf {D}(g)$ .

3. (c) $c_g$ is a bijection $\mathbf {D}(g)\to \mathbf {D}(g^{-1})$ , and $c_{g^{-1}}=(c_g)^{-1}$ .

4. (d) $\mathcal {L}=\mathbf {D}(\mathbf {1})$ , and $x^{\mathbf {1}}=x$ for each $x\in \mathcal {L}$ .

Proof. By Definition 1.1(4), $g\circ \emptyset \circ g^{-1}=g\circ g^{-1}\in \mathbf {D}$ , so $\mathbf {1}\in \mathbf {D}(g)$ and then $\mathbf {1}^g=\mathbf {1}$ by Lemma 1.4(c). Thus (a) holds. Now let $x\in \mathbf {D}(g)$ , and set $w=(g^{-1},x,g)$ . Then $w\in \mathbf {D}$ , and $w^{-1}=(g^{-1},x^{-1},g)$ by definition in Definition 1.1. Then Definition 1.1(4) yields $w^{-1}\circ w\in \mathbf {D}$ , so $w^{-1}\in \mathbf {D}$ by Definition 1.1(1). This shows that $\mathbf {D}(g)$ is closed under inversion. Also, Definition 1.1(4) yields $\mathbf {1}=\Pi (w^{-1}\circ w)=(x^{-1})^g x^g$ , and then $(x^{-1})^g=(x^g)^{^{-1}}$ by Lemma 1.4(f). This completes the proof of (b).

As $w\in \mathbf {D}$ , Lemma 1.4(d) implies that $g\circ w$ and then $g\circ w\circ g^{-1}$ are in $\mathbf {D}$ . Now Definition 1.1(3) and two applications of Lemma 1.4(d) yield

$$ \begin{align*} gx^gg^{-1}=\Pi(g,g^{-1},x,g,g^{-1})=\Pi((g,g^{-1},x)\circ g\circ g^{-1})=\Pi(g,g^{-1},x)=x. \end{align*} $$

Thus $x^g\in \mathbf {D}(g^{-1})$ with $(x^g)^{g^{-1}}=x$ , and thus (c) holds.

Finally, $\mathbf {1}=\mathbf {1}^{-1}$ by Lemma 1.4(f), and $\emptyset \circ x\circ \emptyset =x\in \mathbf {D}$ for any $x\in \mathcal {L}$ , proving (d).

Definition 1.7. Let $\mathcal {L}$ be a partial group, and let $\mathcal {H}$ be a nonempty subset of $\mathcal {L}$ . Then $\mathcal {H}$ is a partial subgroup of $\mathcal {L}$ (denoted $\mathcal {H}\leq \mathcal {L}$ ) if $\mathcal {H}$ is closed under inversion ( $g\in \mathcal {H}$ implies $g^{-1}\in \mathcal {H}$ ) and closed with respect to products. The latter condition means, of course, that $\Pi (w)\in \mathcal {H}$ whenever $w\in \mathbf {W}(\mathcal {H})\cap \mathbf {D}$ . A partial subgroup $\mathcal {N}$ of $\mathcal {L}$ is a partial normal subgroup of $\mathcal {L}$ (denoted $\mathcal {N}\trianglelefteq \mathcal {L}$ ) if $x^g\in \mathcal {N}$ for all $x\in \mathcal {N}$ and all $g\in \mathcal {L}$ for which $x\in \mathbf {D}(g)$ . We say that $\mathcal {H}$ is a subgroup of $\mathcal {L}$ if $\mathcal {H}\leq \mathcal {L}$ and $\mathbf {W}(\mathcal {H})\subseteq \mathbf {D}$ .

An equivalent way to state the condition for normality, which relies on the notational convention introduced above for interpreting product sets $XYZ$ , is to say that the partial subgroup $\mathcal {N}$ of $\mathcal {L}$ is normal in $\mathcal {L}$ if $g^{-1}\mathcal {N}g\subseteq \mathcal {N}$ for all $g\in \mathcal {L}$ .

We leave it to the reader to check that if $\mathcal {H}\leq \mathcal {L}$ , then $\mathcal {H}$ is indeed a partial group, with $\mathbf {D}(\mathcal {H})=\mathbf {W}(\mathcal {H})\cap \mathbf {D}(\mathcal {L})$ .

Lemma 1.8. Let $\mathcal {H}$ and $\mathcal {K}$ be partial subgroups of a partial group $\mathcal {L}$ , and let $\{\mathcal {H}_i\}_{i\in I}$ be a set of partial subgroups of $\mathcal {L}$ .

1. (a) Each partial subgroup of $\mathcal {H}$ is a partial subgroup of $\mathcal {L}$ .

2. (b) Each partial subgroup of $\mathcal {L}$ that is contained in $\mathcal {H}$ is a partial subgroup of $\mathcal {H}$ .

3. (c) If $\mathcal {H}$ is a subgroup of $\mathcal {L}$ , then $\mathcal {H}\cap \mathcal {K}$ is a subgroup of both $\mathcal {H}$ and $\mathcal {K}$ .

4. (d) Suppose $\mathcal {K}\trianglelefteq \mathcal {L}$ . Then $\mathcal {H}\cap \mathcal {K}\trianglelefteq \mathcal {H}$ . Moreover, $\mathcal {H}\cap \mathcal {K}$ is a normal subgroup of $\mathcal {H}$ if $\mathcal {H}$ is a subgroup of $\mathcal {L}$ .

5. (e) $\bigcap \{\mathcal {H}_i\mid i\in I\}$ is a partial subgroup of $\mathcal {L}$ and is a partial normal subgroup of $\mathcal {L}$ if $\mathcal {H}_i\trianglelefteq \mathcal {L}$ for all i.

Proof. One observes that in all the points (a) through (e), the requisite closure with respect to inversion obtains. Thus, we need only be concerned with products.

1. (a) Let $\mathcal {E}\leq \mathcal {H}$ be a partial subgroup of $\mathcal {H}$ . Then

   $$ \begin{align*}\mathbf{D}(\mathcal{E})=\mathbf{W}(E)\cap\mathbf{D}(\mathcal{H})=\mathbf{W}(E)\cap(\mathbf{W}(\mathcal{H})\cap\mathbf{D}(\mathcal{L})= \mathbf{W}(E)\cap\mathbf{D}(\mathcal{L}), \end{align*} $$
   and (a) follows.

2. (b) Suppose $\mathcal {K}\subseteq \mathcal {H}$ , and let $w\in \mathbf {W}(\mathcal {K})\cap \mathbf {D}(\mathcal {H})$ . As $\mathbf {D}(\mathcal {H})\leq \mathbf {D}(\mathcal {L})$ , and since $\mathcal {K}\leq \mathcal {L}$ by hypothesis, we obtain $\Pi (w)\in \mathcal {K}$ .

3. (c) Assuming now that $\mathcal {H}$ is a subgroup of $\mathcal {L}$ , we have $\mathbf {W}(\mathcal {H})\subseteq \mathbf {D}(\mathcal {L})$ , and then $\mathbf {D}(\mathcal {H}\cap \mathcal {K})\subseteq \mathbf {D}(\mathcal {H})\cap \mathbf {D}(\mathcal {K})$ , so that $\mathcal {H}\cap \mathcal {K}$ is a subgroup of both $\mathcal {H}$ and $\mathcal {K}$ .

4. (d) Let $\mathcal {K}\trianglelefteq \mathcal {L}$ , and let $x\in \mathcal {H}\cap \mathcal {K}$ and $h\in \mathcal {H}$ with $(h^{-1},x,h)\in \mathbf {D}(\mathcal {H})$ . Then $(h^{-1},x,h)\in \mathbf {D}(\mathcal {L})$ , and $x^h\in \mathcal {K}$ . As $\mathcal {H}\leq \mathcal {L}$ , we also have $x^h\in \mathcal {H}$ , so $\mathcal {H}\cap \mathcal {K}\trianglelefteq \mathcal {H}$ . Now suppose further that $\mathcal {H}$ is a subgroup of $\mathcal {L}$ . That is, assume that $\mathbf {W}(\mathcal {H})\subseteq \mathbf {D}(\mathcal {L})$ . Then $\mathbf {W}(\mathcal {H}\cap \mathcal {K})\subseteq \mathbf {D}(\mathcal {L})$ , hence $\mathcal {H}\cap \mathcal {K}$ is a subgroup of $\mathcal {H}$ and evidently a normal subgroup.

5. (e) Set $\mathcal {X}=\bigcap \{\mathcal {H}_i\}_{i\in I}$ . Then $\Pi (w)\in \mathcal {X}$ for all $w\in \mathbf {W}(\mathcal {X})\cap \mathbf {D}(\mathcal {L})$ , so $\mathcal {X}\leq \mathcal {L}$ . The last part of (e) may be left to the reader.

For any subset X of a partial group $\mathcal {L}$ , define the partial subgroup $\langle X\mid \mathcal {L}\,\rangle $ of $\mathcal {L}$ generated by X to be the intersection of the set of all partial subgroups of $\mathcal {L}$ containing X. Then $\langle X\mid \mathcal {L}\,\rangle $ is itself a partial subgroup of $\mathcal {L}$ by Lemma 1.8(e). In Parts I through III of this series, the ambient partial group $\mathcal {L}$ will always be understood, so we shall simply write $\langle X\rangle $ for $\langle X\mid \mathcal {L}>$ .

Lemma 1.9. Let X be a subset of $\mathcal {L}$ such that X is closed under inversion. Set $X_0=X$ , and recursively define $X_n$ for $n>0$ by

$$ \begin{align*}X_n=\{\Pi(w)\mid w\in\mathbf{W}(X_{n-1})\cap\mathbf{D}\}. \end{align*} $$

Then $\langle X\rangle =\bigcup \{X_n\}_{n\geq 0}$ .

Proof. Let Y be the union of the sets $X_i$ . Each $X_i$ is closed under inversion by Lemma 1.4(f), and $Y\neq \emptyset $ since $\mathbf {1}=\Pi (\emptyset )$ . Since Y is closed under products, by construction, we get $Y\leq \langle X\rangle $ , and then $Y=\langle X\rangle $ by the definition of $\langle X\rangle $ .

Lemma 1.10 Dedekind lemma

Let $\mathcal {H}$ , $\mathcal {K}$ and $\mathcal {A}$ be partial subgroups of a partial group $\mathcal {L}$ .

1. (a) If $\mathcal {K}\leq \mathcal {A}$ , then $\mathcal {A}\cap \mathcal {H}\mathcal {K}=(\mathcal {A}\cap \mathcal {H})\mathcal {K}$ .

2. (b) If $\mathcal {H}\leq \mathcal {A}$ , then $\mathcal {A}\cap \mathcal {H}\mathcal {K}=\mathcal {H}(\mathcal {A}\cap \mathcal {K})$ .

Proof. The proof is identical to the proof for binary groups and is left to the reader.

Definition 1.11. Let $\mathcal {L}$ and $\mathcal {L}'$ be partial groups, let $\beta :\mathcal {L}\to \mathcal {L}'$ be a mapping, and let $\beta ^*:\mathbf {W}\to \mathbf {W}'$ be the induced mapping of free monoids. Then $\beta $ is a homomorphism (of partial groups) if

• (H1) $\mathbf {D}\beta ^*\subseteq \mathbf {D}'$ , and

• (H2) $(\Pi (w))\beta =\Pi '(w\beta ^*)$ for all $w\in \mathbf {D}$ .

The kernel of $\beta $ is the set $Ker(\beta )$ of all $g\in \mathcal {L}$ such that $g\beta =\mathbf {1}'$ . We say that $\beta $ is an isomorphism if there exists a homomorphism $\beta ':\mathcal {L}'\to \mathcal {L}$ such that $\beta \circ \beta '$ and $\beta '\circ \beta $ are identity mappings. (Equivalently, $\beta $ is an isomorphism if $\beta $ is bijective and $\mathbf {D}\beta =\mathbf {D}'$ .)

Example 1.12. Let $\mathcal {L}=\{\mathbf {1},a,b\}$ be the partial group from Example 1.2, let $\mathcal {L}'$ be any partial group, and let $x\in \mathcal {L}'$ . Then the mapping $\beta :\mathcal {L}\to \mathcal {L}'$ given by

$$ \begin{align*}\mathbf{1}\mapsto\mathbf{1}', \quad a\mapsto x, \quad b\mapsto x^{-1} \end{align*} $$

is a homomorphism. In fact, $\beta $ is the unique homomorphism $\mathcal {L}\to \mathcal {L}'$ , which maps a to x, by the following lemma. Thus, $\mathcal {L}$ is the (unique up to a unique invertible homomorphism) free partial group on one generator. Free partial groups in general can be obtained as ‘free products’ of copies of $\mathcal {L}$ (see Appendix A).

Lemma 1.13. Let $\beta :\mathcal {L}\to \mathcal {L}'$ be a homomorphism of partial groups. Then $\mathbf {1}\beta =\mathbf {1}'$ , and $(g^{-1})\beta =(g\beta )^{-1}$ for all $g\in \mathcal {L}$ .

Proof. Since $\mathbf {1} \mathbf {1}=\mathbf {1}$ , (H1) and (H2) yield $\mathbf {1}\beta =(\mathbf {1}\mathbf {1})\beta =(\mathbf {1}\beta )(\mathbf {1}\beta )$ , and then $\mathbf {1}\beta =\mathbf {1}'$ by left or right cancellation. Since $(g,g^{-1})\in \mathbf {D}$ for any $g\in \mathcal {L}$ by Lemma 1.4(d), (H1) yields $(g\beta ,(g^{-1})\beta )\in \mathbf {D}'$ , and then $\mathbf {1}\beta =(gg^{-1})\beta =(g\beta )((g^{-1})\beta )$ by (H2). As $\mathbf {1}\beta =\mathbf {1}'=(g\beta )(g\beta )^{-1}$ , left cancellation yields $(g^{-1})\beta =(g\beta )^{-1}$ .

Lemma 1.14. Let $\beta :\mathcal {L}\to \mathcal {L}'$ be a homomorphism of partial groups, and set $\mathcal {N}=Ker(\beta )$ . Then $\mathcal {N}$ is a partial normal subgroup of $\mathcal {L}$ .

Proof. By Lemma 1.13, $\mathcal {N}$ is closed under inversion. For w in $\mathbf {W}(\mathcal {N})\cap \mathbf {D}$ , the map $\beta ^*:\mathbf {W}\to \mathbf {W}'$ sends w to a word of the form $(\mathbf {1}',\cdots ,\mathbf {1}')$ . Then $\Pi '(w\beta ^*)=\mathbf {1}'$ by Lemma 1.4(c), and thus $\Pi (w)\in \mathcal {N}$ and $\mathcal {N}$ is a partial subgroup of $\mathcal {L}$ . Now let $f\in \mathcal {L}$ , and let $g\in \mathcal {N}\cap \mathbf {D}(f)$ . Then

$$ \begin{align*} (f^{-1},g,f)\beta^*=((f\beta)^{-1},{\mathbf{1}}',f\beta) \quad\text{(by Lemma 1.13)}, \end{align*} $$

so that

$$ \begin{align*} (g^f)\beta=\Pi'((f^{-1},g,f)\beta^*)=\Pi'((f\beta)^{-1},\mathbf{1}',f\beta)=\mathbf{1}' \end{align*} $$

(again using Lemma 1.4(c)). Thus $\mathcal {N}\trianglelefteq \mathcal {L}$ .

It will be shown later (compare Theorem 4.6) that partial normal subgroups of ‘localities’ are always kernels of homomorphisms.

Lemma 1.15. Let $\beta :\mathcal {L}\to \mathcal {L}'$ be a homomorphism of partial groups, and let M be a subgroup of $\mathcal {L}$ . Then $M\beta $ is a subgroup of $\mathcal {L}'$ .

Proof. We are given $\mathbf {W}(M)\subseteq \mathbf {D}(\mathcal {L})$ , so $\beta ^*$ maps $\mathbf {W}(M)$ into $\mathbf {D}(\mathcal {L}')$ .

Lemma 1.16. Let G and $G'$ be groups (and hence also binary groups in the sense of Lemma 1.3). A map $\alpha :G\to G'$ is a homomorphism of partial groups if and only if $\alpha $ is a homomorphism of binary groups.

Proof. We leave to the reader the proof that if $\alpha $ is a homomorphism of partial groups, then $\alpha $ is a homomorphism of binary groups. Now suppose that $\alpha $ is a homomorphism of binary groups. As $\mathbf {W}(G)=\mathbf {D}(G)$ (and similarly for $G'$ ), it is immediate that $\alpha ^*$ maps $\mathbf {D}(G)$ into $\mathbf {D}(G)$ . Assume that $\alpha $ is not a homomorphism of partial groups, and let $w\in \mathbf {D}(G)$ be of minimal length subject to $\Pi '(w\alpha ^*)\neq (\Pi (w))\alpha $ . Then $n>1$ , and we can write $w=u\circ v$ with both u and v nonempty. Then

$$ \begin{align*}\Pi'(w\alpha^*)=\Pi'(u\alpha^*\circ v\alpha^*)=\Pi'(u\alpha^*)\Pi'(v\alpha^*)=((\Pi(u))\alpha)((\Pi(v))\alpha)=(\Pi(u)\Pi(v))\alpha, \end{align*} $$

as $\alpha $ is a homomorphism of binary groups. Since $(\Pi (u)\Pi (v))\alpha =(\Pi (w))\alpha $ , the proof is complete.

2 Objective partial groups and localities

Recall the convention: if X is a subset of the partial group $\mathcal {L}$ , and $g\in \mathcal {L}$ , then any statement involving the expression ‘ $X^g$ ’ is to be understood as carrying the assumption that $X\subseteq \mathbf {D}(g)$ . Thus, the statement ‘ $X^g=Y$ ’ means $(g^{-1},x,g)\in \mathbf {D}$ for all $x\in X$ , and Y is the set of products $g^{-1} xg$ with $x\in X$ .

Definition 2.1. Let $\mathcal {L}$ be a partial group. For any collection $\Delta $ of subgroups of $\mathcal {L}$ , define $\mathbf {D}_\Delta $ to be the set of all $w=(g_1,\cdots ,g_n)\in \mathbf {W}(\mathcal {L})$ such that

• (*) there exists $(X_0,\cdots ,X_n)\in \mathbf {W}(\Delta )$ with $(X_{i-1})^{g_i}=X_i$ for all i ( $1\leq i\leq n$ ).

Then $\mathcal {L}$ is objective if there exists a set $\Delta $ of subgroups of $\mathcal {L}$ such that the following two conditions hold:

• (O1) $\mathbf {D}=\mathbf {D}_{\Delta }$ .

• (O2) Whenever X and Y are in $\Delta $ and $g\in \mathcal {L}$ such that $X^g$ is a subgroup of Y, then every subgroup of Y containing $X^g$ is in $\Delta $ .

We also say that $\Delta $ is a set of objects for $\mathcal {L}$ if (O1) and (O2) hold.

It will often be convenient to somewhat over-emphasise the role of $\Delta $ in the above definition by saying that ‘ $(\mathcal {L},\Delta )$ is an objective partial group’. By this, we mean $\mathcal {L}$ is an objective partial group and $\Delta $ is a set (there will often be more than one) of objects for $\mathcal {L}$ .

We mention that the condition (O2) requires more than that $X^g$ be a subset of Y in order to conclude that overgroups of X in Y are objects. This is a nonvacuous distinction, since the conjugation map $c_g:X\to X^g$ need not send X to a subgroup of $\mathcal {L}$ in a general partial group.

Example 2.2. Let G be a group, let S be a subgroup of G, and let $\Delta $ be a collection of subgroups of S such that $S\in \Delta $ . Assume that $\Delta $ satisfies (O2). That is, assume that $Y\in \Delta $ for every subgroup Y of S such that $X^g\leq Y$ for some $X\in \Delta $ and some $g\in G$ . Let $\mathcal {L}$ be the set of all $g\in G$ such that $S\cap S^g\in \Delta $ , and let $\mathbf {D}$ be the subset $\mathbf {D}_\Delta $ of $\mathbf {W}(\mathcal {L})$ . Then $\mathcal {L}$ is a partial group (via the multivariable product in G and the inversion in G), and $(\mathcal {L},\Delta )$ is an objective partial group. Specifically,

1. (a) If $\Delta =\{S\}$ , then $\mathcal {L}=N_G(S)$ (so $\mathcal {L}$ is a group in this case).

2. (b) Take $G=O_4^+(2)$ . Thus, G is a semidirect product $V\rtimes S$ , where V is elementary abelian of order 9 and S is a dihedral group of order 8 acting faithfully on V. Let $\Delta $ be the set of all nonidentity subgroups of S. One may check that $S\cap S^g\in \Delta $ for all $g\in G$ , and hence $\mathcal {L}=G$ (as sets). But $\mathcal {L}$ is not a group, as $\mathbf {D}_\Delta \neq \mathbf {W}(G)$ .

3. (c) Take $G=GL_3(2)$ and $S\in Syl_2(G)$ , and let $M_1$ and $M_2$ be the two maximal subgroups of G containing S. Set $P_i=O_2(M_i)$ , and set $\Delta =\{S,P_1,P_2\}$ . Then $\mathcal {L}=M_1\cup M_2$ (in fact the ‘free amalgamated product’ of $M_1$ and $M_2$ over S in the category of partial groups). On the other hand, if $\Delta $ is taken to be the set of all nonidentity subgroups of S, then $\mathcal {L}$ is somewhat more complicated. Its underlying set is $M_1M_2\cup M_2M_1$ .

In an objective partial group $(\mathcal {L},\Delta )$ , we say that the word $w=(g_1,\cdots ,g_n)$ is in $\mathbf {D}$ via $(X_0,\cdots ,X_n)$ if the condition (*) in Definition 2.1 applies specifically to w and $(X_0,\cdots ,X_n)$ . We may also say, more simply, that w is in $\mathbf {D}$ via $X_0$ , since the sequence $(X_0,\cdots ,X_n)$ is determined by w and $X_0$ .

For any partial group $\mathcal {L}$ and subgroups $X,Y$ of $\mathcal {L}$ , set

$$ \begin{align*} N_{\mathcal{L}}(X,Y)=\{g\in\mathcal{L}\mid X\subseteq\mathbf{D}(g),\ X^g\subseteq Y\}, \end{align*} $$

and set

$$ \begin{align*} N_{\mathcal{L}}(X)=\{g\in\mathcal{L}\mid X^g=X\}. \end{align*} $$

Lemma 2.3. Let $(\mathcal {L},\Delta )$ be an objective partial group.

1. (a) $N_{\mathcal {L}}(X)$ is a subgroup of $\mathcal {L}$ for each $X\in \Delta $ .

2. (b) Let $g\in \mathcal {L}$ , and let $X\in \Delta $ with $Y:=X^g\in \Delta $ . Then $N_{\mathcal {L}}(X)\subseteq \mathbf {D}(g)$ , and

   $$ \begin{align*}c_g:N_{\mathcal{L}}(X)\to N_{\mathcal{L}}(Y) \end{align*} $$
   is an isomorphism of groups. More generally,

3. (c) Let $w=(g_1,\cdots ,g_n)\in \mathbf {D}$ via $(X_0,\cdots ,X_n)$ . Then

   $$ \begin{align*}c_{g_1}\circ\cdots\circ c_{g_n}=c_{\Pi(w)} \end{align*} $$
   as isomorphisms from $N_G(X_0)$ to $N_G(X_n)$ .

Proof.

1. (a) Let $X\in \Delta $ , and let $u\in \mathbf {W}(N_{\mathcal {L}}(X))$ . Then $u\in \mathbf {D}$ via X, $\mathbf {1}\in N_{\mathcal {L}}(X)$ (Lemma 1.6(d)), and $N_{\mathcal {L}}(X)^{-1}=N_{\mathcal {L}}(X)$ (Lemma 1.6(c)).

2. (b) Let $x,y\in N_{\mathcal {L}}(X)$ , and set $v=(g^{-1},x,g,g^{-1},y,g)$ . Then (with assistance from Lemma 1.6(c)) $v\in \mathbf {D}$ via Y, and then $\Pi (v)=(xy)^g=x^gy^g$ (using points (a) and (b) of Lemma 1.4). Thus, the conjugation map $c_g:N_{\mathcal {L}}(X)\to N_{\mathcal {L}}(Y)$ is a homomorphism of binary groups (see Lemma 1.3). Since $c_{g^{-1}}=c_g^{-1}$ by Lemma 1.6(c), $c_g$ is an isomorphism of groups.

3. (c) Let $x\in N_{\mathcal {L}}(X_0)$ , set $u_x=w^{-1}\circ (x)\circ w$ and observe (using Lemma 1.6(c)) that $u_x\in \mathbf {D}$ via $X_n$ . Then $\Pi (u_x)$ can be written as $(\cdots (x)^{g_1}\cdots )^{g_n}$ , and this yields (c).

The next lemma provides two basic computational tools.

Lemma 2.4. Let $(\mathcal {L},\Delta )$ be an objective partial group.

1. (a) Let $(a,b,c)\in \mathbf {D}$ , and set $d=abc$ . Then $bc=a^{-1} d$ and $ab=dc^{-1}$ (and all of these products are defined).

2. (b) Let $(f,g)\in \mathbf {D}$ , and let $X\in \Delta $ . Suppose that both $X^f$ and $X^{fg}$ are in $\Delta $ . Then $X^{fg}=(X^f)^g$ .

Proof. Point (a) is a fact concerning partial groups in general and is immediate from Lemma 1.4(c). Now consider the setup in (b). As $(f,g)\in \Delta $ , we also have $(f^{-1},f,g)\in \Delta $ and $g=\Pi (f^{-1},f,g)=f^{-1}(fg)$ . Now observe that $(f^{-1},fg)\in \mathbf {D}$ via $P^f$ , and apply Lemma 2.3(c) to obtain $X^{fg}=((X^f)^{f^{-1}})^{fg}=(X^f)^g$ .

The following result and its corollary are fundamental to the entire enterprise. The proof given here is due to Bernd Stellmacher.

Proposition 2.5. Let $(\mathcal {L},\Delta )$ be an objective partial group. Suppose that $\Delta $ is a collection of subgroups of some $S\in \Delta $ . For each $g\in \mathcal {L}$ , define $S_g$ to be the set of all $x\in \mathbf {D}(g)\cap S$ such that $x^g\in S$ . Then

1. (a) $S_g\in \Delta $ . In particular, $S_g$ is a subgroup of S.

2. (b) The conjugation map $c_g:S_g\to (S_g)^g$ is an isomorphism of groups, and $S_{g^{-1}}=(S_g)^g$ .

3. (c) $P^g$ is defined and is a subgroup of S for every subgroup P of $S_g$ . In particular, $P^g\in \Delta $ for any $P\in \Delta $ with $P\leq S_g$ .

Proof. Fix $g\in \mathcal {L}$ . Then the word $(g)$ of length 1 is in $\mathbf {D}$ by Definition 1.1(2), and since $\mathbf {D}=\mathbf {D}_\Delta $ by (O1), there exists $X\in \Delta $ such that $Y:=X^g\in \Delta $ . Let $a\in S_g$ , and set $b=a^g$ . Then $X^a$ and $Y^b$ are subgroups of S (as $a,b\in S$ ), so $X^a$ and $Y^b$ are in $\Delta $ by (O2). Then $(a^{-1},g,b)\in \mathbf {D}$ via $X^a$ , so also $(g,b)\in \mathbf {D}$ . Also $(a,g)\in \mathbf {D}$ via $X^{a^{-1}}$ . Since $g^{-1} ag=b$ , we get $ag=gb$ by Lemma 2.4(a), and hence

$$ \begin{align*}a^{-1} gb=a^{-1}(gb)=a^{-1}(ag)=(a^{-1} a)g=g \end{align*} $$

by $\mathbf {D}$ -associativity. Since $a^{-1} gb$ conjugates $X^a$ to $Y^b$ by Lemma 2.3(c), we draw the following conclusion.

1. (1) $X^a\leq S_g$ and $(X^a)^g\in \Delta $ for all $a\in S_g$ .

Now let $c,d\in S_g$ . Then (1) shows that both $X^c$ and are members of $\Delta $ that are conjugated to members of $\Delta $ by g. Setting $w=(g^{-1},c,g,g^{-1},d,g)$ , we conclude (by following $X^g$ along the chain of conjugations given by w) that $w\in \mathbf {D}$ via $X^g$ . Then $\mathbf {D}$ -associativity yields

(2) $$ \begin{align} \Pi(w)=(cd)^g=c^g d^g. \end{align} $$

Since $c^g$ and $d^g$ are in S, we conclude that $cd\in S_g$ . Since $S_g$ is closed under inversion by Lemma 1.6(b), $S_g$ is a subgroup of S. As $X\leq S_g\leq S$ , where X and S are in $\Delta $ , (O2) now yields $S_g\in \Delta $ . Thus (a) holds.

Since $c_{g^{-1}}=(c_g)^{-1}$ by Lemma 1.6(c), it follows that $S_{g^{-1}}=(S_g)^g$ . Points (b) and (c) are then immediate from (a) and Lemma 2.3(b).

Corollary 2.6. Assume the hypothesis of Proposition 2.5, let $w=(g_1,\cdots ,g_n)\in \mathbf {W}(\mathcal {L})$ , and define $S_w$ to be the set of all $x\in S$ such that, for all k with $1\leq k\leq n$ , the composition $c_{g_1}\circ \cdots \circ c_{g_k}$ is defined on x and maps x into S. Then $S_w$ is a subgroup of S, and $S_w\in \Delta $ if and only if $w\in \mathbf {D}$ .

Proof. Let $x_0,y_0\in S_w$ , and let $\sigma =(x_0,\cdots ,x_n)$ and $\tau =(y_0,\cdots ,y_n)$ be the corresponding sequences of elements of S, obtained from $x_0$ and $y_0$ via the sequence of maps $c_{g_1}\circ \cdots \circ c_{g_k}$ . Set $S_j=S_{g_j} (1\leq j\leq n)$ . Then $x_{i-1}$ and $y_{i-1}$ are elements of $S_{i-1}$ , so $x_{i-1}y_{i-1}\in S_{i-1}$ by Proposition 2.5(a). As $c_{g_i}$ restricts to a homomorphism on $S_{i-1}$ (see Lemma 2.3(b)), it follows that $x_iy_i\in S_i$ . Thus $S_w$ is closed under the binary product in S. That $S_w$ is closed under inversion is given by Lemma 1.6(c), so $S_w$ is a subgroup of S.

Suppose that $S_w\in \Delta $ , set $P_0=S_w$ , and recursively define $P_k$ for $0\langle k\leq n$ by $P_k=(P_{k-1})^{g_k}$ . Then $P_k$ is a subgroup of S by Proposition 2.5(c) and induction on k. Then (O2) yields $P_k\in \Delta $ , so $w\in \mathbf {D}$ by (O1). Conversely, if $w\in \mathbf {D}$ , then (O1) shows that $P\leq S_w$ for some $P\in \Delta $ , and then $S_w\in \Delta $ by (O2).

Henceforth our focus will be on finite objective partial groups of a certain kind. Here is the main definition.

Definition 2.7. Let p be a prime, and let $\mathcal {L}$ be a finite partial group. Then $\mathcal {L}$ is a locality if there exists a p-subgroup S of $\mathcal {L}$ and a set $\Delta $ of subgroups of S such that

• (L1) $(\mathcal {L},\Delta )$ is objective.

• (L2) S is in $\Delta $ , and S is maximal in the set (partially ordered by inclusion) of p-subgroups of $\mathcal {L}$ .

As with Definition 2.1, we shall tend to over-emphasise the roles of S and of $\Delta $ by saying that ‘ $(\mathcal {L},\Delta ,S)$ is a locality’ when, strictly speaking, we mean only that $\mathcal {L}$ is a locality and that S and $\Delta $ fulfil the conditions (L1) and (L2). (The extent to which S and $\Delta $ are determined by $\mathcal {L}$ is explored in Definition 2.15 and Proposition 2.16 below.)

Notice that if $\mathcal {L}$ is a locality, then the hypothesis of Proposition 2.5 and Corollary 2.6 is fulfilled and we may therefore speak of the subgroups $S_g$ and $S_w$ of S for any $g\in \mathcal {L}$ and any $w\in \mathbf {W}(\mathcal {L})$ .

Lemma 2.8. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $w=(x_1,\cdots ,x_n)\in \mathbf {D}$ , and let $(g_0,\cdots ,g_n)\in \mathbf {W}(N_{\mathcal {L}}(S))$ . Then

(*) $$ \begin{align} (g_0,x_1,g_1^{-1},g_1,x_2,\cdots,x_{n-1},g_{n-1}^{-1},g_{n-1},x_n,g_n)\in\mathbf{D}. \end{align} $$

In particular, conjugation by $g\in N_{\mathcal {L}}(S)$ is an automorphism of the partial group $\mathcal {L}$ .

Proof. Set $P=(S_w)^{g_0^{-1}}$ . One then observes that the word displayed in (*) is in $\mathbf {D}$ via P. Now fix $g\in N_{\mathcal {L}}(S)$ . Applying (*) with $\ell (w)=1$ and with $g_0=g^{-1}$ and $g=g_1$ , we conclude that there is a well-defined mapping $\alpha :\mathcal {L}\to \mathcal {L}$ given by conjugation by g. To show that $\alpha $ is a homomorphism, we need to check that the induced map $\alpha _*:\mathbf {W}(\mathcal {L})\to \mathbf {W}(\mathcal {L})$ sends $\mathbf {D}$ into $\mathbf {D}$ and that

(**) $$ \begin{align} \Pi(w\alpha^*)=\Pi(w)\alpha. \end{align} $$

Set

$$ \begin{align*}u=(g^{-1},x_1,g,g^{-1},x_2,\cdots,x_{n-1},g,g^{-1},x_n,g). \end{align*} $$

Applying (*) with $g^{-1}$ in the role of $g_i$ for all i then yields $u\in \mathbf {D}$ via $P^g$ . Now set $v=((x_1)^g,\cdots ,(x_n)^g)$ . Then $\Pi (v)=\Pi (u)=\Pi (w)^g$ by $\mathbf {D}$ -associativity, and this yields (**). Replacing g with $g^{-1}$ yields the homomorphism $\alpha ^{-1}$ by Lemma 1.6(c), and thus $\alpha $ is an automorphism of $\mathcal {L}$ .

Lemma 2.9. Let $(\mathcal {L},\Delta ,S)$ be a locality, and let $P\in \Delta $ . Then there exists $g\in \mathcal {L}$ such that $N_S(P)\leq S_g$ and such that $N_S(P^g)$ is a Sylow p-subgroup of $N_{\mathcal {L}}(P^g)$ .

Proof. Observe first of all that by (L2), the lemma holds for $P=S$ and $g=\mathbf {1}$ . Among all P for which the lemma fails to hold, choose P so that first $|P|$ and then $|N_S(P)|$ is as large as possible. Set $R=N_S(P)$ , and let $R^*$ be a Sylow p-subgroup of $N_{\mathcal {L}}(P)$ containing R. Then $R<R^*$ (proper subgroup), and then also $R<N_{R^*}(R)$ . We have $P\neq R$ as $P\neq S$ , and then the maximality of $|P|$ yields the existence of an element $f\in N_{\mathcal {L}}(R,S)$ with $N_S(R^f)\in Syl_p(N_{\mathcal {L}}(R^f))$ .

By Lemma 2.3(b), f-conjugation induces an isomorphism

$$ \begin{align*}N_{\mathcal{L}}(R)\xrightarrow{c_f} N_{\mathcal{L}}(R^f). \end{align*} $$

By Sylow’s theorem, there exists $x\in N_{\mathcal {L}}(R^f)$ such that $(N_{R^*}(R)^f)^x\leq N_S(R^f)$ . Here $(f,x)\in \mathbf {D}$ via R, so Lemma 2.3(c) yields $(N_{R^*}(R)^f)^x=N_{R^*}(R)^{fx}$ . Thus, by replacing f with $fx$ , we may assume that f was chosen to begin with so that $N_{R^*}(R)^f\leq N_S(R^f)$ . Since $R^*$ normalises P and $c_f$ is an isomorphism, it follows that $N_{R^*}(R)^f$ normalises $P^f$ , and thus $|N_S(P^f)|>|N_S(P)|$ . The maximality of $|N_S(P)|$ in the choice of P then implies that $P^f$ is not a counterexample to the lemma. Set $Q=P^f$ . Thus there exists $h\in N_{\mathcal {L}}(N_S(Q),S)$ such that $N_S(Q^h)$ is a Sylow subgroup of $N_{\mathcal {L}}(Q^h)$ . Here $(f,h)\in \mathbf {D}$ via R, so $Q^h=P^g$ , where $g=fh$ , so P is not a counterexample to the lemma, and therefore no counterexample exists.

Proposition 2.10. Let $(\mathcal {L},\Delta ,S)$ be a locality, and let H be a subgroup of $\mathcal {L}$ .

1. (a) There exists an object $P\in \Delta $ such that $H\leq N_{\mathcal {L}}(P)$ . Indeed, there exists a unique largest such P. $($ All subgroups are ‘local subgroups’. $)$

2. (b) Let P be the largest $P\in \Delta $ as in (a). Then there exists $w\in \mathbf {W}(H)$ such that $P=S_w$ .

3. (c) If H is a p-subgroup of $\mathcal {L}$ , then there exists $g\in \mathcal {L}$ such that $H^g\leq S$ .

Proof. For any $w=(h_1,\cdots ,h_n)\in \mathbf {W}(H)$ , let $w'$ be the word $(g_1,\cdots ,g_n)$ defined by $g_i=h_1\cdots h_i$ . As H is finite, we may choose w so as to maximise the cardinality of the set $X=\{g_1,\cdots ,g_n\}$ . Suppose that $X\neq H$ , let $g\in H-X$ , and set $h=\Pi (w)^{-1} g$ . Then the set of entries of $(w\circ (h))'$ is $X\cup \{g\}$ , contrary to the maximality of X. Thus $X=H$ .

We have $\mathbf {W}(H)\subseteq \mathbf {D}$ as H is a subgroup of $\mathcal {L}$ , and thus $w\in \mathbf {D}$ via some $P\in \Delta $ . Then $P^{g_i}=P^{h_1\cdots h_i}\leq S$ for all i, so $P^h\leq S$ for all $h\in H$ . Set $U=\langle P^h\mid h\in H\rangle $ (the subgroup of S generated by the union of all $P^h$ for $h\in H$ ). Then $U\in \Delta $ by (O2). To complete the proof of (a) and (b) it now suffices to show that $H\leq N_{\mathcal {L}}(U)$ , and for this it is enough to observe that, by Lemma 2.4(b), $(P^f)^g$ is defined and is equal to $P^{fg}$ for all $f,g\in H$ .

Assume now that H is a p-group. By Lemma 2.9, there exist $V\in \Delta $ and $g\in \mathcal {L}$ such that $V=U^g$ and $N_S(V)\in Syl_p(N_{\mathcal {L}}(V))$ . Let $c_g:N_{\mathcal {L}}(U)\to N_{\mathcal {L}}(V)$ be the isomorphism given by Lemma 2.3(b). Thus $H^g$ is a p-subgroup of $N_{\mathcal {L}}(V)$ , so there exists $x\in N_{\mathcal {L}}(V)$ with $(H^g)^x\leq N_S(V)$ . Since $(g,x)\in \mathbf {D}$ via U, we may apply Lemma 2.3(c), obtaining $(H^g)^x=H^{gx}$ . Thus (c) holds with $gx$ in the role of g.

The theory being developed here purports to be ‘p-local’, so it is important to be able to analyse the structure of $N_{\mathcal {L}}(U)$ for U an arbitrary subgroup of S (not necessarily in $\Delta $ ). Since our policy in this Part I is to avoid bringing in the language of fusion systems, we shall obtain for now only the following very limited result concerning such normalisers.

Lemma 2.12. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $R\leq S$ be a subgroup of S, and set $\Gamma =\{N_P(R)\mid P\in \Delta \}$ . Then

1. (a) $N_{\mathcal {L}}(R)$ is a partial subgroup of $\mathcal {L}$ .

2. (b) If $\Gamma \subseteq \Delta $ , then $(N_{\mathcal {L}}(R),\Gamma )$ is an objective partial group.

3. (c) If $\Gamma \subseteq \Delta $ and $N_S(R)$ is a maximal p-subgroup of $N_{\mathcal {L}}(R)$ , then $(N_{\mathcal {L}}(R),\Gamma ,S)$ is a locality.

In particular, if $R\trianglelefteq S$ , then $(N_{\mathcal {L}}(R),\Delta ,S)$ is a locality.

Proof. Set $\mathcal {L}_R=N_{\mathcal {L}}(R)$ . Then Lemma 2.3(c) shows that $\Pi $ maps $\mathbf {W}(\mathcal {L}_R)\cap \mathbf {D}$ into $\mathcal {L}_R$ , while Lemma 1.6(c) shows that $\mathcal {L}_R$ is closed under the inversion in $\mathcal {L}$ . Thus $\mathcal {L}_R$ is a partial subgroup of $\mathcal {L}$ .

Let $\mathbf {D}(\mathcal {L}_R)$ be the domain of the product in the partial group $\mathcal {L}_R$ . Then $\mathbf {D}(\mathcal {L}_R)=\mathbf {W}(\mathcal {L}_R)\cap \mathbf {D}$ , by definition. Assume now that $\Gamma \subseteq \Delta $ , and let $w\in \mathbf {D}(\mathcal {L}_R)$ via some $P\in \Delta $ . Then $w\in \mathbf {D}(\mathcal {L}_R)$ via $N_P(R)$ , and thus $\mathcal {L}_R$ satisfies the condition (O1) for objectivity in Definition 2.1. Also, as $\Gamma \subseteq \Delta $ , we have $\Gamma =\{P\in \Delta \mid P\leq N_S(R)\}$ , so $\Gamma $ is closed in the sense of condition (O2) in Definition 2.1. This yields (b). Point (c) is then immediate from Definition 2.7.

Lemma 2.13. Let $(\mathcal {L},\Delta ,S)$ be a locality, and set

$$ \begin{align*}O_p(\mathcal{L})=\bigcap\{S_w\mid w\in\mathbf{W}(\mathcal{L})\}. \end{align*} $$

Then $O_p(\mathcal {L})$ is the unique largest subgroup of S that is a partial normal subgroup of $\mathcal {L}$ .

Proof. Set $Y=O_p(\mathcal {L})$ , let $g\in \mathcal {L}$ , and let $w\in \mathbf {W}(\mathcal {L})$ . Then $Y\leq S_g$ and $Y\leq S_{(g)\circ w}$ , so $Y^g\leq S_w$ . Thus $Y^g\leq Y$ , so $Y\trianglelefteq \mathcal {L}$ .

Now let $X\leq S$ with $X\trianglelefteq \mathcal {L}$ . Then $X\trianglelefteq S$ . Let $g\in \mathcal {L}$ , and set $P=S_g$ . Then conjugation by g is defined on $N_{\mathcal {L}}(P)$ by Lemma 2.3(b), so $N_X(P)^g$ is defined, and then $N_X(P)^g\leq X$ as $X\trianglelefteq \mathcal {L}$ . Thus $N_X(P)^g\leq S$ , so $N_X(P)\leq S_g$ . As $S_gX=PX$ is a subgroup of S, it follows that $X\leq P$ , so $X^g=X$ , and $X\leq O_p(\mathcal {L})$ .

Given a locality $\mathcal {L}$ , there can be more than one choice for S and, after that, more than one choice for $\Delta $ , such that $\mathbf {D}=\mathbf {D}_\Delta $ .

Definition 2.14. Let $\mathcal {L}$ be a partial group. An automorphism $\alpha $ of $\mathcal {L}$ is inner if there exists $g\in \mathcal {L}$ such that $\alpha $ is given by conjugation by g. That is,

1. (1) $x\in \mathcal {L} \implies x^g$ is defined and is equal to $x\alpha $ , and

2. (2) $(x_1,\cdots ,x_n)\in \mathbf {D} \implies (x_1^g,\cdots ,x_n^g)\in \mathbf {D}$ and $x_1^g\cdots x_n^g=(x_1\cdots x_n)^g$ .

Write $Inn(\mathcal {L})$ for the set of all inner automorphisms of $\mathcal {L}$ .

Definition 2.15. Let $\mathcal {L}$ be a locality, and let S be a p-subgroup of $\mathcal {L}$ . Then S is a Sylow p-subgroup of $\mathcal {L}$ if there exists a set $\Delta $ of subgroups of S such that $(\mathcal {L},\Delta ,S)$ satisfies the conditions (L1) and (L2) of Definition 2.7. Write $Syl_p(\mathcal {L})$ for the set of Sylow p-subgroups of $\mathcal {L}$ .

It will be convenient to introduce some notation regarding ‘conjugation’ by words $w\in (\mathcal {L})$ in the case of a locality $(\mathcal {L},\Delta ,S)$ . Thus, let $w=(g_1,\cdots ,g_n)\in \mathbf {W}(\mathcal {L})$ , and let X be a subgroup of $S_w$ . For each $x=x_0\in X$ and each index i from $1$ to n, there is then an element $x_i\in S$ defined by $x_i=(x_{i-1})^{g_i}$ , and we may write $x^w$ for $x_n$ . The mapping $x\mapsto x^w$ may be written as

$$ \begin{align*}c_w: X\to X^w. \end{align*} $$

Proposition 2.16. Let $(\mathcal {L},\Delta ,S)$ be a locality, and let K be the set of all $g\in \mathcal {L}$ such that conjugation by g is an inner automorphism of $\mathcal {L}$ .

1. (a) K is a subgroup of $\mathcal {L}$ .

2. (b) For each $w=(x_1,\cdots ,x_n)\in \mathbf {D}$ and each $(g_0,\cdots ,g_n)\in \mathbf {W}(K)$ , we have

   (*) $$ \begin{align} (g_0,x_1,g_1^{-1},g_1,x_2,\cdots,g_{n-1}^{-1},g_{n-1},x_n,g_n)\in\mathbf{D}. \end{align} $$

3. (c) Set $Q=O_p(K)$ . Then $Q\in \Delta $ and $K=N_{\mathcal {L}}(Q)$ . Moreover, for each $w\in \mathbf {D}$ , there exists $P\leq Q\cap S_w$ such that $P\in \Delta $ and $P^w\leq Q$ .

4. (d) $Syl_p(\mathcal {L})=Syl_p(K)$ .

5. (e) $Inn(\mathcal {L})\trianglelefteq Aut(\mathcal {L})$ , and every automorphism of $\mathcal {L}$ can be factored as an inner automorphism followed by an automorphism that leaves S invariant.

Proof. Write $\mathcal {S}$ for $Syl_p(\mathcal {L})$ . For $S'\in \mathcal {S}$ , note that $N_{\mathcal {L}}(S')$ is a subgroup of $\mathcal {L}$ . By Lemma 2.8, the condition (*) holds with $N_{\mathcal {L}}(S')$ in the role of K. Let $\mathcal {U}$ be the union (taken over all $S'\in \mathcal {S}$ ) of the groups $N_{\mathcal {L}}(S')$ , and let H be the partial subgroup of $\mathcal {L}$ generated by $\mathcal {U}$ . The above observation concerning Lemma 2.8 together with a straightforward argument by induction on word length then yields $\mathbf {W}(\mathcal {U})\subseteq \mathbf {D}$ , and thus H is a subgroup of $\mathcal {L}$ . Moreover, $\mathbf {W}(\mathcal {U})$ has the following property: For any $(g_1,\cdots ,g_n)\in \mathbf {D}(\mathcal {L})$ and any $(u_0,\cdots ,u_n)$ with each $u_i\in \mathbf {W}(\mathcal {U})$ , the word

$$ \begin{align*}u_0\circ g_1\circ u_1^{-1}\circ u_1\circ g_2\circ\cdots\circ u_{n-1}^{-1}\circ u_{n-1}\circ g_n\circ u_n \end{align*} $$

is in $\mathbf {D}$ by induction on the sum of the lengths of the words $u_i$ . The condition (*) then holds with H in the role of K, by $\mathbf {D}$ -associativity. In particular, conjugation by $g\in H$ is an automorphism of $\mathcal {L}$ , and thus H is a subset of K.

Now let $g\in K$ . Then $(\mathcal {L},\Delta ^g,S^g)$ is a locality, so $S^g\in \mathcal {S}$ . Then $S^g\in Syl_p(H)$ , and there exists $h\in H$ with $S^g=S^h$ . The product $gh^{-1}$ is defined, and then $gh^{-1}\in N_{\mathcal {L}}(S)$ . Thus $gh^{-1}\in H$ , so $g\in H$ , and we conclude that $H=K$ . This completes the proof of (a), (b) and (d). Point (e) is immediate from (d), so it remains only to prove (c).

By Proposition 2.10(a), K normalises a member of $\Delta $ . Then, since $S\in Syl_p(K)$ , we obtain $Q:=O_p(K)\in \Delta $ . By Proposition 2.10(b), there exists a word $u\in \mathbf {W}(K)$ such that $Q=S_u$ . Then also $Q=S_{u^{-1}}$ . Let $w\in \mathbf {D}$ , and let $f\in N_{\mathcal {L}}(Q)$ . The word $v:=u\circ w\circ u$ is in $\mathbf {D}$ by (*), and clearly $S_v\leq Q$ and $S_{v^{-1}}\leq Q$ . Set $P=(S_v)^{\Pi (u)}$ . Then $P\leq S_w\cap Q$ and $P^{\Pi (w)}\leq Q$ . As $S_v\in \Delta $ , we have $P\in \Delta $ . Write $w=(x_1,\cdots ,x_n)$ . Then

$$ \begin{align*} (f^{-1},x_1,f,f^{-1},\cdots,f,f^{-1},x_n,f)\in\mathbf{D}\ \ \text{via } P^f, \end{align*} $$

and this shows that conjugation by f is an inner automorphism of $\mathcal {L}$ . Thus $K=N_{\mathcal {L}}(Q)$ , and the proof is complete.

Lemma 2.17. Let $\mathcal {L}$ be a locality, and let S be a Sylow p-subgroup of $\mathcal {L}$ . Then there is a unique smallest set $\Delta =\Delta _0$ and a unique largest set $\Delta =\Delta _1$ of subgroups of S such that the conditions (L1) and (L2) of Definition 2.7 are satisfied by $(\mathcal {L},\Delta ,S)$ .

Proof. Take $\Delta _0$ to be the overgroup-closure in S of the set of all $S_w$ for $w\in \mathbf {D}$ . Take $\Delta _1$ to be the union of all the sets $\Gamma $ of subgroups of S that fulfil (L1) and (L2).

3 Partial normal subgroups

Throughout this section, we fix a locality $(\mathcal {L},\Delta ,S)$ and a partial normal subgroup $\mathcal {N}\trianglelefteq \mathcal {L}$ . Recall that this means that $\mathcal {N}\leq \mathcal {L}$ is a partial subgroup of $\mathcal {L}$ and $\Pi (g^{-1},x,g)\in \mathcal {N}$ for all $x\in \mathcal {N}$ and all $g\in \mathcal {L}$ for which $(g^{-1},x,g)\in \mathbf {D}$ . Set $T=S\cap \mathcal {N}$ .

Lemma 3.1.

1. (a) Let $g\in \mathcal {L}$ , and let $P\leq S_g$ . Then $(T\cap P)^g=T\cap P^g$ . In particular, we have $(T\cap S_g)^g\leq T$ .

2. (b) Let $x\in \mathcal {N}$ , and let P be a subgroup of $S_x$ . Then $PT=P^x T$ .

3. (c) T is maximal in the poset of p-subgroups of $\mathcal {N}$ .

Proof.

1. (a) Let $g\in \mathcal {L}$ , let $P\leq S_g$ , and let $t\in T\cap P$ . Then $t^g\in S$ , and $t^g\in \mathcal {N}$ as $\mathcal {N}\trianglelefteq \mathcal {L}$ . Thus $t^g\in T$ , so

   (*) $$ \begin{align} (T\cap P)^g\leq T\cap P^g. \end{align} $$
   Now replace g with $g^{-1}$ and replace P with the subgroup $P^g$ of $S_{g^{-1}}$ . Then (*) becomes the statement
   (**) $$ \begin{align} (T\cap P^g)^{g^{-1}}\leq T\cap P. \end{align} $$
   Conjugating (**) by g yields $T\cap P^g\leq (T\cap P)^g$ , and thus (*) is an equality, as required.

2. (b) Let $a\in P$ . Then $(P^x)^a\leq S$ and $P^a=P$ . Setting $w=(a^{-1},x^{-1},a,x)$ , we then have $w\in \mathbf {D}$ via $P^{xa}$ . Now $\Pi (w)=a^{-1} a^x\in S$ , while also $\Pi (w)=(x^{-1})^ax\in \mathcal {N}$ , so $\Pi (w)\in T$ . Then $a^x\in aT$ , and we have thus shown that $P^x\leq PT$ . Then $P^x T\leq PT$ . The reverse inequality is given (as in the proof of (a)) by replacing x with $x^{-1}$ and replacing P with $P^x$ .

3. (c) Let R be a p-subgroup of $\mathcal {N}$ containing T. By Proposition 2.10(c), there exists $g\in \mathcal {L}$ with $R^g\leq S$ , and then $R^g\leq S\cap \mathcal {N}=T$ . As $T^g=T$ and conjugation by g is injective, we conclude that $R=T$ .

Lemma 3.2. Let $x,y\in \mathcal {N}$ , and let $f\in N_{\mathcal {L}}(T)$ .

1. (a) If $(x,f)\in \mathbf {D}$ , then $(f,f^{-1},x,f)\in \mathbf {D}$ , $xf=fx^f$ , and $S_{(x,f)}=S_{(f,x^f)}=S_x\cap S_f$ .

2. (b) If $(f,y)\in \mathbf {D}$ , then $(f,y,f^{-1},f)\in \mathbf {D}$ , $fy=y^{f^{-1}}f$ , and $S_{(f,y)}=S_{(y^{f^{-1}},f)}=S_{y^{f^{-1}}}\cap S_f$ .

Proof. Set $Q=S_{(x,f)}$ and $P=S_x\cap S_f$ . As $x\in \mathcal {N}$ , we have $Q^xT=QT$ by Lemma 3.1(b). Then since $f\in N_{\mathcal {L}}(T)$ , we obtain $QT\leq S_f$ . Thus $Q\leq P$ . But also $P^xT=PT$ , so $P=Q$ . Now $(f,f^{-1},x,f)\in \mathbf {D}$ via Q, and $\Pi (f,f^{-1},x,f)=xf=fx^f$ . We have

$$ \begin{align*}Q=S_f\cap S_x = S_{(f,f^{-1},x,f)}\leq S_{(f,x^f)}, \end{align*} $$

so in order to complete the proof of (a), it remains to show that $S_{(f,x^f)}\leq Q$ .

On the other hand, in addressing (b), set $R=S_{(f,y)}$ . Then Lemma 3.1(b) yields $R^{fy}T=R^fT$ , so that $R^{fy}T\leq \leq S_{f^{-1}}$ . Set $v=(f,y,f^{-1},f)$ . Then $v\in \mathbf {D}$ via R, and we have $R=S_v$ . Now $\mathbf {D}$ -associativity yields $fy=\Pi (v)=y^{f^{-1}}f$ . In the special case that $y=x^f$ , we obtain

$$ \begin{align*}R=S_{(f,x^f)}=S_{(f,x^f,f^{-1},f)}\leq S_{(x,f)}=Q, \end{align*} $$

completing the proof of (a). The remainder of (b) now follows as an application of (a) to $(y^{f^{-1}},f)$ , and the remainder of (b) as an application of (a) to $(y^{f^{-1}},f)$ .

Lemma 3.3. Let $w\in \mathbf {W}(N_{\mathcal {L}}(T))\cap \mathbf {D}$ , set $g=\Pi (w)$ , and let $x,y\in \mathcal {N}$ .

1. (a) Suppose that $(x)\circ w\in \mathbf {D}$ , and set $P=S_{(x)\circ w}$ . Then $u:=w\circ w^{-1}\circ (x)\circ w\in \mathbf {D}$ , and $S_u=P^g$ .

2. (b) Suppose that $w\circ (y)\in \mathbf {D}$ , and set $Q=S_{w\circ (y)}$ . Then $v:=w\circ (y)\circ w^{-1}\circ w\in \mathbf {D}$ , and $S_v=Q$ .

Proof. We prove only (a), leaving it to the reader to supply a similar argument for (b). As $P^xT=PT$ by Lemma 3.1(b), and since both $P^x$ and T are contained in $S_w$ , we have $P\leq S_w$ . Then $P^g\leq S$ by Lemma 2.3(c), and $P^g\leq S_u$ . In particular, $u\in \mathbf {D}$ via $P^g$ . As $S_u\leq S_{w^{-1}}$ , and $(S_u)^{g^{-1}}\leq P$ , we obtain $S_u\leq P^g$ . Thus $S_u=P^g$ .

Lemma 3.4. Let $w=(f_1,g_1,\cdots ,f_n,g_n)\in \mathbf {D}$ , with $f_i\in N_{\mathcal {L}}(T)$ and with $g_i\in \mathcal {N}$ for all i. Set $u=(f_1,\cdots ,f_n)$ . Then there exists $g\in \mathcal {N}$ such that

(*) $$ \begin{align} S_w\leq S_{u\circ(g)}\ \ \text{and}\ \ \Pi(w)=\Pi(u\circ(g)). \end{align} $$

Similarly, there exists $g'\in \mathcal {N}$ such that

(**) $$ \begin{align} S_w\leq S_{(g')\circ u}\ \ \text{and}\ \ \Pi(w)=\Pi((g')\circ u). \end{align} $$

Proof. The case $n=1$ is given by Lemma 3.2. For the general case, write

$$ \begin{align*}w=(f_1,g_1)\circ w_1, \end{align*} $$

and set $u_1=(f_2,\cdots ,f_n)$ . Induction on n implies that there exists $x_1\in \mathcal {N}$ such that $S_{w_1}\leq S_{u_1\circ (x_1)}$ and $\Pi (w_1)=\Pi (u_1\circ (x_1))$ . Set

$$ \begin{align*}w'=(f_1,g_1)\circ u_1\circ(x_1). \end{align*} $$

Thus $S_w\leq S_{w'}$ , and we have $\Pi (w)=\Pi (w')$ by $\mathbf {D}$ -associativity. Apply Lemma 3.3(a) to the word $(g_1)\circ u_1$ to obtain (*). A similar argument in which one begins by writing $w=w_n\circ (f_n,g_n)$ yields (**).

The following result will be of fundamental importance in Part III.

Lemma 3.5. Suppose that

(*) $$ \begin{align} C_{N_{\mathcal{L}}(P)}(O_p(N_{\mathcal{L}}(P)))\leq O_p(N_{\mathcal{L}}(P))\quad\text{for all } P\in\Delta \text{ with } T\leq P. \end{align} $$

Then $N_{\mathcal {N}}(T)\leq N_{\mathcal {L}}(C_S(T)T)\leq N_{\mathcal {L}}(C_S(T))$ .

Proof. Let $g\in N_{\mathcal {N}}(T)$ , and set $P=S_g$ . Then $P^g=P$ by Lemma 3.1(b). Set $M=N_{\mathcal {L}}(P)$ , $K=\mathcal {N}\cap M$ and $D=N_{C_S(T)}(P)$ . Here M is a subgroup of $\mathcal {L}$ as $P\in \Delta $ , and then K is a normal subgroup of M by Definition 1.7(d). We have $T\trianglelefteq M$ by Lemma 3.1(a), so $D\leq C_M(T)$ , and then $[K,D]\leq C_K(T)$ . Notice that $T\in Syl_p(K)$ by Lemma 3.1(c), so that $K/T$ is a $p'$ -group. Then $C_K(T)=Z(T)\times Y$ , where Y is a $p'$ -group; and thus Y is a normal $p'$ -subgroup of M. Then $[O_p(M),Y]=1$ , so $Y\leq O_p(M)$ by hypothesis, and thus $Y=1$ . We then have $[K,D]\leq T$ , so $[g,D]\leq T$ , and $D\leq P$ . As $C_S(T)P$ is a p-group we thereby obtain $C_S(T)\leq P$ . This shows that $C_S(T)$ is g-invariant for all $g\in \mathcal {N}_{\mathcal {N}}(T)$ and yields the lemma.

Definition 3.6. Let $\mathcal {L}\circ \Delta $ be the set of all pairs $(f,P)\in \mathcal {L}\times \Delta $ such that $P\leq S_f$ . Define a relation $\uparrow $ on $\mathcal {L}\circ \Delta $ by $(f,P)\uparrow (g,Q)$ if there exist elements $x\in N_{\mathcal {N}}(P,Q)$ and $y\in N_{\mathcal {N}}(P^f,Q^g)$ such that $xg=fy$ .

This relation may be indicated by means of a commutative square

(*)

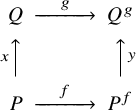
of conjugation maps, labeled by the conjugating elements, and in which the horizontal arrows are isomorphisms and the vertical arrows are injective homomorphisms. The relation $(f,P)\uparrow (g,Q)$ may also be expressed by

$$ \begin{align*} w:=(x,g,y^{-1},f^{-1})\in\mathbf{D} \text{ via } P, \text{ and } \Pi(w)=\mathbf{1}. \end{align*} $$

It is easy to see that $\uparrow $ is reflexive and transitive. We say that $(f,P)$ is maximal in $\mathcal {L}\circ \Delta $ if $(f,P)\uparrow (g,Q)$ implies that $|P|=|Q|$ . As S is finite, there exist maximal elements in $\mathcal {L}\circ \Delta $ . Since $(f,P)\uparrow (f,S_f)$ for $(f,P)\in \mathcal {L}\circ \Delta $ , we have $P=S_f$ for every maximal $(f,P)$ . For this reason, we will say that f is $\uparrow $ -maximal in $\mathcal {L}$ (with respect to $\mathcal {N}$ ) if $(f,S_f)$ is maximal in $\mathcal {L}\circ \Delta $ .

Lemma 3.7. Let $f\in \mathcal {L}$ .

1. (a) If $f\in N_{\mathcal {L}}(S)$ , then f is $\uparrow $ -maximal.

2. (b) If f is $\uparrow $ -maximal, then so is $f^{-1}$ .

3. (c) If f is $\uparrow $ -maximal and $(f,S_f)\uparrow (g,Q)$ , then g is $\uparrow $ -maximal, $Q=S_g$ , and $(g,Q)\uparrow (f,S_f)$ .

Proof. Point (a) is immediate from Definition 3.6. Now suppose that f is $\uparrow $ -maximal, and let $g\in \mathcal {L}$ with $(f^{-1},S_{f^{-1}})\uparrow (g^{-1},S_{g^{-1}})$ . Since $S_{f^{-1}}=(S_f)^f$ and $S_{g^{-1}}=(S_g)^g$ , one obtains a diagram

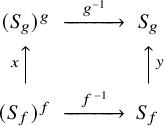
as in Definition 3.6, from which it is easy to read off the relation $(f,S_f)\uparrow (g,S_g)$ . Then $|S_f|=|S_g|$ as f is $\uparrow $ -maximal, and then also $|S_{f^{-1}}|=|S_{g^{-1}}|$ . Thus $f^{-1}$ is $\uparrow $ -maximal, and (b) holds. Point (c) is immediate from the transitivity of $\uparrow $ .

Lemma 3.8. Let $(g,Q),(h,R)\in \mathcal {L}\circ \Delta $ with $(g,Q)\uparrow (h,R)$ , and suppose that $T\leq R$ . Then there exists a unique $y\in \mathcal {N}$ with $g=yh$ . Moreover,

1. (a) $Q^y\leq R$ , and $Q\leq S_{(y,h)}$ .

2. (b) If $N_T(Q^g)\in Syl_p(N_{\mathcal {N}}(Q^g))$ , then $N_T(Q^y)\in Syl_p(N_{\mathcal {N}}(Q^y))$ .

Proof. By definition of the relation $\uparrow $ , there exist elements $u\in N_{\mathcal {N}}(Q,R)$ and $v\in N_{\mathcal {N}}(Q^g,R^h)$ such that $(u,h,v^{-1},g^{-1})\in \mathbf {D}$ via Q and $\Pi (w)=\mathbf {1}$ .

In particular, $uh=gv$ . Since $T\leq R$ , points (a) and (b) of Lemma 3.1 yield

$$ \begin{align*} T=T^h, Q^uT=QT\leq R, \text{ and } Q^gT=Q^{gv}T\leq R^h. \end{align*} $$

Then

$$ \begin{align*} w:=(u,h,v^{-1},h^{-1})\in\mathbf{D}\quad{\text via}\quad (Q,Q^u,Q^{uh},Q^{uhv^{-1}}=Q^g,Q^{gh^{-1}}). \end{align*} $$

Set $y=\Pi (w)$ . Then $y=u(v^{-1})^{h^{-1}}\in N_{\mathcal {N}}(Q,R)$ . Since $(u,h,v^{-1},h^{-1},h)$ and $(g,v,v^{-1})$ are in $\mathbf {D}$ (as $\mathcal {L}$ is a partial group), we get $yh=uhv^{-1}=g$ . This yields (a). The uniqueness of y is given by right cancellation.

Suppose now that $N_T(Q^g)\in Syl_p(N_{\mathcal {N}}(Q^g))$ . As $N_T(Q^y)^h=N_T(Q^g)$ , it follows from Lemma 2.3(b) that $N_T(Q^y)\in Syl_p(N_{\mathcal {N}}(Q^y))$ .

Proposition 3.9. Let $g\in \mathcal {L}$ and suppose that g is $\uparrow $ -maximal with respect to $\mathcal {N}$ . Then $T\leq S_g$ .

Proof. Set $P=S_g$ and $Q=P^g$ . We first show

1. (1) Let $y\in N_{\mathcal {N}}(P,S)$ . Then $|T\cap P|=|T\cap P^y|$ and $(g,P)\uparrow (y^{-1} g,P^y)$ . In particular, $y^{-1} g$ is $\uparrow $ -maximal.

We have $|T\cap P|=|T\cap P^y|$ by Lemma 3.1(a). The following diagram

(*)

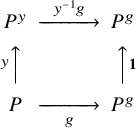
shows that $(g,P)\uparrow (y^{-1} g,P^y)$ , and then $y^{-1} g$ is $\uparrow $ -maximal by Lemma 3.7(c). Thus (1) holds.

Suppose next that $N_T(P)\in Syl_p(N_{\mathcal {N}}(P))$ . Then $N_T(P)^g\in Syl_p(N_{\mathcal {N}}(Q))$ , by Lemma 2.3(b), and there exists $x\in N_{\mathcal {N}}(Q)$ such that $N_T(Q)^x\leq N_T(P)^g$ . Here $(x,g^{-1})\in \mathbf {D}$ via Q, and we get $N_T(Q)^{xg^{-1}}\leq N_T(P)\leq S$ . Thus $(g^{-1},Q)\uparrow (xg^{-1},N_T(Q)Q)$ . As $g^{-1}$ is $\uparrow $ -maximal by Lemma 3.7, it follows that $N_T(Q)\leq Q$ . As $TQ$ is a p-group, we then have $T\leq Q$ , so $T\leq P$ . We have thus shown

1. (2) If $T\nleq P$ , then $N_T(P)\notin Syl_p(N_{\mathcal {N}}(P))$ .

We next show

1. (3) Suppose that there exists $y\in \mathcal {N}$ such that $P\leq S_y$ and such that $N_T(P^y)\in Syl_p(N_{\mathcal {N}}(P^y))$ . Then $T\leq P$ .

Indeed, under the hypothesis of (3), we have $(g,P)\uparrow (y^{-1} g,P^y)$ by (1). Then $(y^{-1} g,P^y)$ is maximal in $\mathcal {L}\circ \Delta $ , and $P^y=S_{y^{-1} g}$ . If $T\nleq P$ , then $T\nleq P^y$ , and then (2) applies to $(y^{-1} g,P^y)$ in the role of $(g,P)$ and yields a contradiction. So, (3) holds.

Among all counterexamples, let g be chosen so that $|P|$ is as large as possible. By Lemma 2.9, there exists $f\in \mathcal {L}$ so that $Q^f\leq S$ and $N_S(Q^f)\in Syl_p(N_{\mathcal {L}}(Q^f))$ . Set $h=gf$ (where the product is defined via P) and set $R=P^h$ . Let $(h',P')$ be maximal in $\mathcal {L}\circ \Delta $ with $(h,P)\uparrow (h',P')$ . We note that since $R=P^h=Q^f$ , we have $N_T(R)\in Syl_p(N_{\mathcal {N}}(R))$ . So, if $T\leq P'$ , then Lemma 3.8(b) applies and yields $h=yh'$ for some $y\in \mathcal {N}$ such that $P\leq S_y$ and such that $N_T(P^y)\in Syl_p(N_{\mathcal {N}}(P^y))$ . The existence of such an element y contradicts (3), so we conclude that $T\nleq P'$ . Then $(h',P')$ is a counterexample to the proposition, and the maximality of $|P|$ yields $|P|=|P'|$ . Then $(h,P)$ is maximal in $\mathcal {L}\circ \Delta $ , as is $(h^{-1},R)$ by Lemma 3.7(b), so $T\nleq R$ . But $N_T(R)\in Syl_p(N_{\mathcal {N}}(R))$ , so (2) applies with $(h^{-1},R)$ in the role of $(g,P)$ and yields $T\leq R$ . Then $T\leq P$ , and the proof is complete.

Lemma 3.10. Suppose that $N_{\mathcal {N}}(T)\leq N_{\mathcal {L}}(S)$ . Then every element of $N_{\mathcal {L}}(T)$ is $\uparrow $ -maximal with respect to $\mathcal {N}$ .

Proof. Let $f\in N_{\mathcal {L}}(T)$ , and set $P=S_f$ . Then $T\leq P$ and $T\leq P^f$ . Let $(g,Q)\in \mathcal {L}\circ \Delta $ with $(f,P)\uparrow (g,Q)$ , and let $x,y\in \mathcal {N}$ be chosen as in Definition 3.6. Then $P\leq Q$ by Proposition 3.9, and we have $P=P^x$ and $(P^f)^y=P^f\leq Q^g$ by Lemma 3.1(b). To show that f is $\uparrow $ -maximal, it suffices now to show that $P=Q$ , and hence it suffices to show that $N_Q(P)\leq P$ .

Set $D=N_Q(P)$ . Then $T\leq P\leq D\leq S_x$ , so Lemma 3.1(b) implies that $x\in N_{\mathcal {L}}(D)$ . Since $y\in N_{\mathcal {N}}(T)\leq N_{\mathcal {L}}(S)$ , we obtain $(x,g,y^{-1})\in \mathbf {D}$ via D. As $xg=fy$ by the setup of Definition 3.6, we then have $xgy^{-1}=f$ by Lemma 1.3(g), and thus $D\leq S_f$ . That is, we have $N_Q(P)\leq P$ , as required.

If X and Y are subsets of $\mathcal {L}$ , then one has the notion of the product $XY$ , introduced in Section 1, as the set of all $\Pi (x,y)$ with $(x,y)\in \mathbf {D}\cap (X\times Y)$ .

Corollary 3.11 Frattini lemma

Let $(\mathcal {L},\Delta ,S)$ be a locality, let $\mathcal {N}\trianglelefteq \mathcal {L}$ be a partial normal subgroup, and let $\Lambda $ be the set of $\uparrow $ -maximal elements of $\mathcal {L}$ with respect to $\mathcal {N}$ . Then $\mathcal {L}=\mathcal {N}\Lambda =\Lambda \mathcal {N}$ . In particular, we have $\mathcal {L}=N_{\mathcal {L}}(T)\mathcal {N}=\mathcal {N} N_{\mathcal {L}}(T)$ .

Proof. Let $f\in \mathcal {L}$ , set $P=S_f$ , and choose $(g,Q)\in \mathcal {L}\circ \Delta $ so that $(f,P)\uparrow (g,Q)$ and g is $\uparrow $ -maximal. By Proposition 3.9, we have $\Lambda \subseteq N_{\mathcal {L}}(T)$ and $T\leq S_g=Q$ , so Lemma 3.8 yields $f=xg$ for some $x\in \mathcal {N}$ , and then Lemma 3.2 shows that $f=gy$ , where $y=x^g$ .

The following result will be seen to play a crucial role in the theory being developed here. It was discovered and proved by Stellmacher in his reading of an early draft of [Ch1]. The proof given here is his.

Lemma 3.12 (splitting lemma)

Let $(x,f)\in \mathbf {D}$ with $x\in \mathcal {N}$ and with $f \ \uparrow $ -maximal with respect to $\mathcal {N}$ . Then $S_{(x,f)}=S_{xf}=S_{(f,x^f)}$ .

Proof. Set $Q=S_{(x,f)}$ . Since $f\in N_{\mathcal {L}}(T)$ by Proposition 3.9, we may appeal to Lemma 3.2(a) and obtain

1. (1) $y:=x^f$ is defined and, upon setting $g=xf$ , we have $g=fy$ and $Q=S_{(f,y)}$ .

Thus, the problem is to show that $Q=S_g$ . By (1), we have $Q\leq S_f\cap S_g$ , and Lemma 3.2(a) yields the further result that $Q=S_f\cap S_x$ . Set

$$ \begin{align*}P_0=N_{S_f}(Q),\ \ P_1=N_{S_g}(Q),\ \ P=\langle P_0,P_1\rangle, \end{align*} $$

and set $R=P_0\cap P_1$ . Then $Q\leq R$ . In fact, Lemma 2.3(b) shows that $y=f^{-1} g$ and that $(R^f)^y=R^g$ , so $R\leq Q$ , and thus $P_0\cap P_1=Q$ .

Assume now that $(x,f)$ is a counterexample to the lemma. That is, assume $Q<S_g$ (proper inclusion). Then $Q<P_1$ , so $P_1\nleq P_0$ . Thus

1. (2) $P_1\nleq S_f$ .

We consider two cases, as follows.

Case 1. $x\in N_{\mathcal {L}}(T)$ .

Among all counterexamples to case 1, take $(x,f)$ so that $|Q|$ is as large as possible. As $f\in N_{\mathcal {L}}(T)$ (Lemma 3.5), we have $T\leq Q$ , and then $x\in N_{\mathcal {L}}(Q)$ by Lemma 3.1(b). Thus $Q^g=Q^{xf}=Q^f$ . Set $Q'=Q^g$ . Then Lemma 2.3(b) yields an isomorphism $c_f:N_{\mathcal {L}}(Q)\to N_{\mathcal {L}}(Q')$ . Here $f=x^{-1} g$ so $c_f=c_{x^{-1}}\circ c_g$ by Lemma 2.3(c). As $x\in N_{\mathcal {N}}(Q)\trianglelefteq N_{\mathcal {L}}(Q)$ , we obtain $(P_1)^{x^{-1}}\leq N_{\mathcal {N}}(Q)P_1$ , and then

$$ \begin{align*}(P_1)^f=((P_1)^{x^{-1}})^g\leq (N_{\mathcal{N}}(Q)P_1)^g\leq N_{\mathcal{N}}(Q')N_S(Q'). \end{align*} $$

Also $(P_0)^f\leq N_S(Q')$ , so

1. (3) $P^f\leq N_{\mathcal {N}}(Q')N_S(Q')$ .

Since $T\leq Q'$ , T is a Sylow p-subgroup of $N_{\mathcal {N}}(Q')$ by Lemma 3.1(c), and thus $N_S(Q')$ is a Sylow p-subgroup of $N_{\mathcal {N}}(Q')N_S(Q')$ . By (3) and Sylow’s theorem, there is then an element $v\in N_{\mathcal {N}}(Q')$ such that $P^{fv}\leq N_S(Q')$ . In particular, we have

1. (4) $P_0\leq S_{(f,v)}$ and $P\leq S_{fv}$ .

Set $u=v^{f^{-1}}$ . Then $(u,f)\in \mathbf {D}$ , and we have $uf=fv$ and $S_{(u,f)}=S_{(f,v)}$ by Lemma 3.2. If $S_{(f,v)}=S_{fv}$ , then $(f,v)\in \mathbf {D}$ via P, so that $P\leq S_f$ , contrary to (2). Thus $S_{(f,v)}\neq S_{fv}$ , so $(u,f)$ is a counterexample to the lemma. Then (4) and the maximality of $|Q|$ in the choice of $(x,f)$ yields $Q=P_0=N_{S_f}(Q)$ , so $Q=S_f$ . As $(f,Q)\uparrow (g,P)$ via $(x^{-1},\mathbf {1})$ , we have contradicted the $\uparrow $ -maximality of f.

Case 2. The case $x\notin N_{\mathcal {L}}(T)$ .

Again, among all counterexamples, take $(x,f)$ so that $|Q|$ is as large as possible. Let h be $\uparrow $ -maximal, with $(g,S_g)\uparrow (h,S_h)$ . Then $T\leq S_h$ by Proposition 3.9, and by Lemma 3.8 there exists $r\in \mathcal {N}$ with $g=rh$ . Note that Lemma 3.8(a) also yields $S_g=S_{(r,h)}\geq Q=S_{(x,g)}$ .

Set $w=(f^{-1},x^{-1},r,h)$ , observe that $w\in \mathbf {D}$ via $Q^g$ , and find

$$ \begin{align*}\Pi(w)=(f^{-1} x^{-1})(rh)=g^{-1} g=\mathbf{1}. \end{align*} $$

Then $h=r^{-1} xf$ and $hf^{-1}=r^{-1} x$ by Lemma 2.4(a). Since both f and h are in $N_{\mathcal {L}}(T)$ , we obtain $r^{-1} x\in N_{\mathcal {L}}(T)$ , so $r^{-1} x\in N_{\mathcal {N}}(T)$ . Now case 1 applies, with $(r^{-1} x,f)$ in the role of $(x,f)$ , and thus $S_h=S_{(r^{-1} x,f)}\leq S_f$ (using Lemma 3.2). By definition of $\uparrow $ , there exist $a,b\in \mathcal {N}$ such that one has the usual commutative diagram:

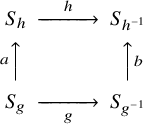
As $T\leq S_h$ , Lemma 3.1(b) yields

$$ \begin{align*}S_g\leq S_gT=(S_g)^aT\leq S_h, \end{align*} $$

so $S_g\leq S_f$ . This again contradicts (1) and completes the proof.

The splitting lemma yields a useful criterion for partial normality, as follows.

Corollary 3.13. Let $\mathcal {L}$ be a locality, let $\mathcal {N}\trianglelefteq \mathcal {L}$ , and let $\mathcal {K}\trianglelefteq \mathcal {N}$ be a partial normal subgroup of $\mathcal {N}$ . Suppose that $\mathcal {K}$ is $N_{\mathcal {L}}(T)$ -invariant. That is, suppose that $x^h\in \mathcal {K}$ for all $(h^{-1},x,h)\in \mathbf {D}$ such that $x\in \mathcal {K}$ and $h\in N_{\mathcal {L}}(T).$ Then $\mathcal {K}\trianglelefteq \mathcal {L}$ .

Proof. Let $x\in \mathcal {K}$ , and let $f\in \mathcal {L}$ such that $x^f$ is defined. By the Frattini lemma, we may write $f=yg$ with $y\in \mathcal {N}$ and with $g \ \uparrow $ -maximal, and then the splitting lemma yields $S_f=S_{(y,g)}$ . Set $u=(f^{-1},x,f)$ and $v=(g^{-1},y^{-1},x,y,g)$ . Then $S_u=S_v\in \Delta $ , and $x^f=\Pi (u)=\Pi (v)=(x^y)^g$ . Thus $x^f\in \mathcal {K}$ , and $\mathcal {K}\trianglelefteq \mathcal {L}$ .

In the notation introduced following Lemma 1.4, for each $f\in \mathcal {L}$ , we have the coset $\mathcal {N}f$ of $\mathcal {N}$ consisting of the elements $\Pi (x,f)$ such that $x\in \mathcal {N}$ and $(x,f)\in \mathbf {D}$ . A coset $\mathcal {N}f$ is called maximal if it is not a proper subset of any coset of $\mathcal {N}$ .

Proposition 3.14. The following hold.

1. (a) $\mathcal {N}f=f\mathcal {N}$ for all $f\in N_{\mathcal {L}}(T)$ , and if f is $\uparrow $ -maximal with respect to $\mathcal {N}$ , then $\mathcal {N}f=\mathcal {N} f\mathcal {N}=f\mathcal {N}$ .

2. (b) Let $f,g\in \mathcal {L}$ , and assume that f is $\uparrow $ -maximal. Then

   $$ \begin{align*}(g,S_g)\uparrow(f,S_f)\ \iff\ \mathcal{N}g\subseteq\mathcal{N}f\ \iff\ g\in\mathcal{N}f. \end{align*} $$

3. (c) If $g\in \mathcal {L}$ is $\uparrow $ -maximal relative to $\mathcal {N}$ , then $\mathcal {N}g$ is a maximal coset of $\mathcal {N}$ . Moreover, every maximal coset of $\mathcal {N}$ is of the form $\mathcal {N}f$ for some $\uparrow $ -maximal element f.

4. (d) $\mathcal {L}$ is partitioned by the set $\mathcal {L}/\mathcal {N}$ of maximal cosets of $\mathcal {N}$ .

5. (e) Let $u:=(g_1,\cdots ,g_n)\in \mathbf {D}$ , and let $v:=(f_1,\cdots ,f_n)$ be a sequence of $\uparrow $ -maximal elements of $\mathcal {L}$ such that $g_i\in \mathcal {N}f_i$ for all i. Then $v\in \mathbf {D}$ via $TS_u$ , and $\Pi (u)\in \mathcal {N}\Pi (v)$ .

Proof.

1. (a) That $\mathcal {N}f=f\mathcal {N}$ for $f\in N_{\mathcal {L}}(T)$ is given by Lemma 3.2. Now let f be $\uparrow $ -maximal (relative to $\mathcal {N}$ ). Then $f\in N_{\mathcal {L}}(T)$ by Proposition 3.9. Let $x,y\in \mathcal {N}$ such that $(x,f,y)\in \mathbf {D}$ . Then $(x,fy)\in \mathbf {D}$ , and $(x,fy)=(x,y'f)$ , where $y'=fyf^{-1}$ . The splitting lemma (Lemma 3.12) then yields $(x,y',f)\in \mathbf {D}$ , and thus $\mathcal {N}f\mathcal {N}\subseteq \mathcal {N}f$ . The reverse inclusion is obvious and yields (a).

2. (b) Suppose that $(g,S_g)\uparrow (f,S_f)$ . By Definition 3.6, there then exist $a,b\in \mathcal {N}$ such that both $(a,f)$ and $(g,b)$ are in $\mathbf {D}$ via $S_g$ and with $af=gb$ . Then $(a,f,b^{-1})\in \mathbf {D}$ via $S_g$ , and $afb^{-1}=g$ . Thus $g\in \mathcal {N}f\mathcal {N}$ , so $g\in \mathcal {N}f$ by (a). Write $g=xf$ with $x\in \mathcal {N}$ . Then Lemma 3.12 yields $S_g=S_{(x,f)}\leq S_f$ . Let $y\in \mathcal {N}$ with $(y,g)\in \mathbf {D}$ . Since $(S_{(y,g)})^y\leq S_g=S_{(x,f)}$ , we get $(y,x,f)\in \mathbf {D}$ , and $yg=(yx)f\in \mathcal {N}f$ . Thus $(g,S_g)\uparrow (f,S_f)\implies \mathcal {N}g\subseteq \mathcal {N}f$ . Clearly $\mathcal {N}g\subseteq \mathcal {N}f\implies g\in \mathcal {N}f$ . The required circle of implications is then completed by Lemma 3.12.

3. (c) Let g be $\uparrow $ -maximal, and let $f\in \mathcal {L}$ with $\mathcal {N}g\subseteq \mathcal {N}f$ . We aim to show that $\mathcal {N}g=\mathcal {N}f$ , so as to conclude that $\mathcal {N}g$ is a maximal coset. To that end, choose $g'\in \mathcal {L}$ so that $g'$ is $\uparrow $ -maximal and $(f,S_f)\uparrow (g',S_{g'})$ . Then (b) yields $\mathcal {N}f\subseteq \mathcal {N}g'$ , and thus $\mathcal {N}g\subseteq \mathcal {N}g'$ . Another application of (b) then yields $(g,S_g)\uparrow (g',S_{g'})$ . As g is $\uparrow $ -maximal, we now get $(g',S_g')\uparrow (g,S_g)$ from Lemma 3.7(c), and then $\mathcal {N}g'\subseteq \mathcal {N}g$ by (b). As $\mathcal {N}f\subseteq \mathcal {N}g'$ , we conclude that $\mathcal {N}f=\mathcal {N}g$ , and thus $\mathcal {N}g$ is a maximal coset.

   Now suppose instead that $g\in \mathcal {L}$ is given so that $\mathcal {N}g$ is a maximal coset, and let $f\in \mathcal {L}$ be $\uparrow $ -maximal with $(g,S_g)\uparrow (f,S_f)$ . Then (b) yields $\mathcal {N}g\subseteq \mathcal {N}f$ , and then $\mathcal {N}g=\mathcal {N}f$ by maximality. Thus (c) holds.

4. (d) Let X and Y be maximal cosets of $\mathcal {N}$ , and let $h\in X\cap Y$ . By (c), we have $X=\mathcal {N}f$ and $Y=\mathcal {N}g$ for some $\uparrow $ -maximal elements f and g. Thus there exist $x,y\in \mathcal {N}$ with $(x,f)\in \mathbf {D}$ , $(y,g)\in \mathbf {D}$ , and with $h=xf=yg$ . Then also $(x^{-1},x,f)\in \mathbf {D}$ , so $(x^{-1},yg)=(x^{-1},xf)\in \mathbf {D}$ . The splitting lemma (Lemma 3.12) then yields $(x^{-1},y,g)\in \mathbf {D}$ , and we thereby obtain $f=x^{-1} yg\in \mathcal {N}g$ . Now (b) implies that $\mathcal {N}f\subseteq \mathcal {N}g$ , and symmetry gives the reverse inclusion. Thus $\mathcal {N}f=\mathcal {N}g$ if $\mathcal {N}f\cap \mathcal {N}g\neq \emptyset $ .

5. (e) Let $x_i\in \mathcal {N}$ with $g_i=f_ix_i$ , and set $w=(f_1,x_1,\cdots ,f_n,g_n)$ . Then $S_{g_i}=S_{(f_i,x_i)}$ by Lemma 3.12, so $S_w=S_u$ . Thus $w\in \mathbf {D}$ , so by Lemma 3.4 there exists $x\in \mathcal {N}$ such that $S_w=S_{v\circ (x)}$ , and with $\Pi (w)=\Pi (v)x$ . Here $T\leq S_v$ by Proposition 3.9, so $TS_u\leq S_v$ . As $\Pi (u)=\Pi (w)$ by $\mathbf {D}$ -associativity, we have $\Pi (u)=\Pi (v)x\in \Pi (v)\mathcal {N}$ . Then $\Pi (u)\in \mathcal {N}\Pi (v)$ by (a).

Lemma 3.15. Let $\mathcal {H}$ be a partial subgroup of the locality $\mathcal {L}$ containing the partial normal subgroup $\mathcal {N}\trianglelefteq \mathcal {L}$ . Then $\mathcal {H}$ is the disjoint union of the maximal cosets of $\mathcal {N}$ contained in $\mathcal {H}$ .

Proof. Let $f\in \mathcal {H}$ . Apply the Frattini lemma (Corollary 3.11) to obtain $f=xh$ for some $x\in \mathcal {N}$ and some $h\in N_{\mathcal {L}}(T)$ such that h is $\uparrow $ -maximal with respect to $\mathcal {N}$ . Then $h=x^{-1} f$ by Lemma 1.4(d), and thus $h\in \mathcal {H}$ as $\mathcal {N}\leq \mathcal {H}$ . Then also $\mathcal {N}h\subseteq \mathcal {H}$ , where $\mathcal {N}h$ is a maximal coset of $\mathcal {N}$ by Proposition 3.14(c).

The set $\mathcal {L}/\mathcal {N}$ of maximal cosets of $\mathcal {N}$ may also be denoted $\bar {\mathcal {L}}$ . Let $\rho :\mathcal {L}\to \bar {\mathcal {L}}$ be the mapping that sends $g\in \mathcal {L}$ to the unique maximal coset of $\mathcal {N}$ containing g. Set $\mathbf {W}:=\mathbf {W}(\mathcal {L})$ and $\bar {\mathbf {W}}=\mathbf {W}(\bar {\mathcal {L}})$ , and let $\rho ^*:\mathbf {W}\to \bar {\mathbf {W}}$ be the induced mapping of free monoids. For any subset or element X of $\mathbf {W}$ , write $\bar X$ for the image of X under $\rho ^*$ . Similarly, if Y is a subset or element of $\mathcal {L}$ , write $\bar Y$ for the image of Y under $\rho $ . In particular, $\bar {\mathbf {D}}$ denotes the image of $\mathbf {D}$ under $\rho ^*$ . Set $\bar {\Delta }=\{\bar P\mid P\in \Delta \}$ .

For $w\in \mathbf {W}$ , we shall say that w is $\uparrow $ -maximal (relative to $\mathcal {N}$ ) if every entry of w is $\uparrow $ -maximal.

Lemma 3.16. There is a unique mapping $\bar \Pi :\bar {\mathbf {D}}\to \bar {\mathcal {L}}$ , and a unique involutory bijection $\bar g\mapsto {\bar g}^{-1}$ on $\bar {\mathcal {L}}$ such that $\bar {\mathcal {L}}$ , with these structures, is a partial group and $\rho $ is a homomorphism of partial groups. Moreover, $\bar {\mathbf {1}}$ is then the identity element of $\bar {\mathcal {L}}$ , and the homomorphism of free monoids $\rho ^*:\mathbf {W}(\mathcal {L})\to \mathbf {W}(\bar {\mathcal {L}})$ maps $\mathbf {D}$ onto $\bar {\mathbf {D}}$ .

Proof. Let $u=(g_1,\cdots ,g_n)$ and $v=(h_1,\cdots ,h_n)$ be members of $\mathbf {D}$ such that $\bar u=\bar v$ . By Proposition 3.14(d), there exists, for each i, an $\uparrow $ -maximal $f_i\in \mathcal {L}$ with $g_i,h_i\in \mathcal {N}f_i$ . Set $w=(f_1,\cdots ,f_n)$ . Then $w\in \mathbf {D}$ by Proposition 3.14(e), which also shows that $\Pi (u)$ and $\Pi (v)$ are elements of $\mathcal {N}\Pi (w)$ . Thus $\bar {\Pi (u)}=\bar {\Pi (w)}=\bar {\Pi (v)}$ , and there is a well-defined mapping $\bar \Pi :\bar {\mathbf {D}}\to \bar {\mathcal {L}}$ given by

(*) $$ \begin{align} \bar\Pi(u)=\bar{\Pi(u)}\quad\text{for all } u\in\mathbf{D}. \end{align} $$

For any subset X of $\mathcal {L}$ , write $X^{-1}$ for the set of inverses of elements of X. For any $f\in \mathcal {L}$ , we then have $(\mathcal {N}f)^{-1}=f^{-1}\mathcal {N}^{-1}$ by Definition 1.1(4). Here $\mathcal {N}^{-1}=\mathcal {N}$ as $\mathcal {N}$ is a partial group, and then $(\mathcal {N}f)^{-1}=\mathcal {N}f^{-1}$ by Proposition 3.14(a). The inversion map $\mathcal {N}f\mapsto \mathcal {N}f^{-1}$ is then well-defined and is an involutory bijection on $\bar {\mathcal {L}}$ . Set $\bar {\mathbf {1}}=\mathcal {N}$ .

We now check that the axioms in Definition 1.1, for a partial group, are satisfied by the above structures. Since $\bar {\mathbf {D}}$ is the image of $\mathbf {D}$ under $\rho ^*$ , we get $\bar {\mathcal {L}}\subseteq \bar {\mathbf {D}}$ . Now let $\bar w=\bar u\circ \bar v\in \bar {\mathbf {D}}$ , let $u,v$ be $\uparrow $ -maximal preimages in $\mathbf {W}$ of $\bar u$ and $\bar v$ , and set $w=u\circ v$ . Then w is $\uparrow $ -maximal, so $w\in \mathbf {D}$ by Proposition 3.14(e). Then u and v are in $\mathbf {D}$ , so $\bar u$ and $\bar v$ are in $\bar {\mathbf {D}}$ . Thus $\bar {\mathbf {D}}$ satisfies Definition 1.1(1). Clearly, (*) implies that $\bar \Pi $ restricts to the identity on $\bar {\mathcal {L}}$ , so $\bar \Pi $ satisfies Definition 1.1(2).

Next, let $\bar u\circ \bar v\circ \bar w\in \bar {\mathbf {D}}$ , and choose corresponding $\uparrow $ -maximal preimages $u,v,w$ . Set $g=\Pi (v)$ . Then $\bar g=\bar \Pi (\bar v)$ by (*). By Definition 1.1(3), we have both $u\circ v\circ w$ and $u\circ (g)\circ w$ in $\mathbf {D}$ , and these two words have the same image under $\Pi $ . Applying $\rho ^*$ , we obtain words in $\bar {\mathbf {D}}$ having the same image under $\bar \Pi $ , and thus $\bar \Pi $ satisfies Definition 1.1(3). By definition, $\bar \Pi (\emptyset )=\bar {\mathbf {1}}$ , and then the condition Definition 1.1(4) is readily verified. Thus, $\bar {\mathcal {L}}$ is a partial group.

By definition, $\bar {\mathbf {D}}$ is the image of $\mathbf {D}$ under $\rho ^*$ . So, in order to check that $\rho $ is a homomorphism of partial groups, it suffices to show that if $w\in \mathbf {D}$ , then $\bar \Pi (w\rho ^*)=\Pi (w)\rho $ . But this is simply the statement (*). Moreover, it is this observation that establishes that the given partial group structure on $\bar {\mathcal {L}}$ is the unique one for which $\rho $ is a homomorphism of partial groups. We have $f\in Ker(\rho )$ if and only if $f\rho =\bar {\mathbf {1}}=\mathcal {N}$ . Since $\mathcal {N}f\subseteq \mathcal {N}$ implies $f\in \mathcal {N}$ , and since $\mathcal {N}$ is the maximal coset of $\mathcal {L}$ containing $\mathbf {1}$ , we obtain $Ker(\rho )=\mathcal {N}$ .

4 Quotient localities

We continue the setup in which $(\mathcal {L},\Delta ,S)$ is a fixed locality and $\mathcal {N}\trianglelefteq \mathcal {L}$ is a partial normal subgroup. We have seen in Lemma 3.16 that the set $\mathcal {L}/\mathcal {N}$ of maximal cosets of $\mathcal {N}$ inherits from $\mathcal {L}$ a partial group structure via the projection map $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ . The aim now is to go further and show that $\mathcal {L}/\mathcal {N}$ is a locality. The argument for this involves some subtleties: the main problem lies in showing that $\mathbf {D}(\mathcal {L}/\mathcal {N})$ contains $\mathbf {D}_{\bar {\Delta }}$ (see Definition 2.1), where $\bar {\Delta }$ is the set of all $P\rho $ with $P\in \Delta $ . The following two lemmas are intended as steps toward addressing this point.

Lemma 4.1. Let $(\mathcal {L},\Delta ,S)$ be a locality, and let $\mathcal {N}\trianglelefteq \mathcal {L}$ . Then $(\mathcal {N}S,\Delta ,S)$ is a locality.

Proof. By Lemma 3.4, $\mathcal {N}S$ is a partial subgroup of $\mathcal {L}$ . One observes that $\mathbf {D}(\mathcal {N}S)$ is the subset $\mathbf {D}_\Delta $ of $\mathbf {W}(\mathcal {N}S)$ , as defined in (Definition 2.1), and this suffices to show that $(\mathcal {N}S,\Delta )$ is objective. As S is a maximal p-subgroup of $\mathcal {N}S$ , there is nothing more that needs to be shown.

Lemma 4.2. Let P be a subgroup of S, let $\Gamma $ be a nonempty set of S-conjugates of P, and set $X=\bigcup \Gamma $ . Assume that $P^x\in \Gamma $ for all $x\in X$ . Then either $\Gamma =\{P\}$ or $N_S(P)\cap X\nsubseteq P$ .

Proof. Let $\S $ be the set of overgroups Q of P in S such that $X\cap Q=P$ . Thus $P\in \S $ . Regard $\S $ as a poset via inclusion, and let Q be maximal in $\S $ . If $Q=S$ , then $X=P$ and $\Gamma =\{P\}$ . On the other hand, suppose that $Q\neq S$ . Then Q is a proper subgroup of $N_S(Q)$ , and the maximality of Q implies that there exists $x\in N_S(Q)\cap X$ with $x\notin P$ . Since $P^x\leq Q$ , and since $P^x\subseteq X$ by hypothesis, we conclude that $P^x=P$ . Thus $N_S(P)\cap X\nsubseteq P$ .

Theorem 4.3. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $\bar {\mathcal {L}}$ be a partial group, and let $\beta :\mathcal {L}\to \bar {\mathcal {L}}$ be a homomorphism of partial groups such that the induced map $\beta ^*:\mathbf {W}(\mathcal {L})\to \mathbf {W}(\bar {\mathcal {L}})$ sends $\mathbf {D}(\mathcal {L})$ onto $\mathbf {D}(\bar {\mathcal {L}})$ . Set $\mathcal {N}=Ker(\beta )$ and $T=S\cap \mathcal {N}$ . Further, set $\mathbf {D}=\mathbf {D}(\mathcal {L})$ , $\bar {\mathbf {D}}=\mathbf {D}(\bar {\mathcal {L}})$ , $\bar S=S\beta $ , and $\bar \Delta =\{P\beta \mid P\in \Delta \}$ . Then $(\bar {\mathcal {L}},\bar \Delta ,\bar S)$ is a locality. Moreover,

1. (a) The fibres of $\beta $ are the maximal cosets of $\mathcal {N}$ .

2. (b) For each $\bar w\in \mathbf {W}(\bar {\mathcal {L}})$ , there exists $w\in \mathbf {W}(\mathcal {L})$ such that $\bar w=w\beta ^*$ and each entry of w is $\uparrow $ -maximal relative to the partial normal subgroup $\mathcal {N}$ of $\mathcal {L}$ . For any such w, we then have $w\in \mathbf {D}$ if and only if $\bar w\in \bar {\mathbf {D}}$ .

3. (c) Let $P,Q\in \Delta $ with $T\leq P\cap Q$ . Then $\beta $ restricts to a surjection $N_{\mathcal {L}}(P,Q)\to N_{\bar {\mathcal {L}}}(P\beta ,Q\beta )$ and a surjective homomorphism if $P=Q$ .

4. (d) $\beta $ is an isomorphism if and only if $\mathcal {N}=1$ .

5. (e) We have $(S_g)\beta =\bar S_{g\beta }$ for each $g\in \mathcal {L}$ such that g is $\uparrow $ -maximal with respect to $\mathcal {N}$ .

Proof. As $\mathbf {D}\beta ^*=\bar {\mathbf {D}}$ , it follows that $\beta ^*$ maps the set of words of length 1 in $\mathcal {L}$ onto the set of words of length 1 in $\bar {\mathcal {L}}$ . Thus $\beta $ is surjective.

For any subgroup M of $\mathcal {L}$ , there is a homomorphism of partial groups $\beta _M:M\to M\beta $ given by restriction of $\beta $ , and then $\beta _M$ is a homomorphism of groups by Lemma 1.13. In particular, we have the homomorphism $\beta _S:S\to \bar S$ , so $\bar S$ is a p-group, and $\bar \Delta $ is a set of subgroups of $\bar S$ .

We have $\mathcal {N}\trianglelefteq \mathcal {L}$ by Lemma 1.14. Let $\Lambda $ be the set of elements $g\in \mathcal {L}$ such that g is $\uparrow $ -maximal relative to $\mathcal {N}$ . For any $g\in \Lambda $ , $\beta $ is constant on the maximal coset $\mathcal {N}g$ (see Proposition 3.14) of $\mathcal {N}$ , so $\beta $ restricts to a surjection of $\Lambda $ onto $\bar {\mathcal {L}}$ , and hence $\beta ^*$ restricts to a surjection of $\mathbf {W}(\Lambda )$ onto $\mathbf {W}(\bar {\mathcal {L}})$ . If $\bar w\in \bar {\mathbf {D}}$ , then there exists $w\in \mathbf {D}$ with $w\beta ^*=\bar w$ , and then Proposition 3.14(e) shows that such a w may be chosen to be in $\mathbf {W}(\Lambda )$ . In particular, (b) holds, and

1. (1) $\beta ^*$ maps $\mathbf {D}\cap \mathbf {W}(\Lambda )$ onto $\bar {\mathbf {D}}$ .

Let $\bar a\in \bar S$ , let $a\in S$ be a $\beta _S$ -preimage of $\bar a$ , and let $h\in \mathcal {L}$ be any $\beta $ -preimage of $\bar a$ . Then $(h,a^{-1},a)\in \mathbf {D}$ via $S_h$ , and we have $h=(ha^{-1})a\in \mathcal {N}a$ . Thus

1. (2) The $\beta $ -preimage of an element $\bar a\in \bar S$ is a maximal coset $\mathcal {N}a$ , where $a\in S$ .

Fix $\bar g\in \bar {\mathcal {L}}$ , let $g\in \Lambda $ with $g\beta =\bar g$ , set $P=S_g$ , and set

$$ \begin{align*}\bar S_{\bar g}=\{\bar x\in\bar S\mid \bar x^{\bar g}\in \bar S\}. \end{align*} $$

Let $\bar a\in \bar S_{\bar g}$ , set $\bar b=\bar g^{-1}\bar a\bar g$ , and choose $a,b\in S$ so that $a\beta =\bar a$ and $b\beta =\bar b$ . As $(g^{-1},g,b)\in \mathbf {D}$ , we may apply left cancellation within $\bar {\mathcal {L}}$ and obtain $\bar g\bar b=\bar a\bar g$ . A further, similar, left cancellation then yields $\bar a^{-1}\bar g\bar b=\bar g$ . Let $x\in S_g$ , and set $v=(b^{-1},g^{-1},a,a^{-1},x,a,a^{-1},g,b)$ . Then $v\in \mathbf {D}$ by Lemma 2.8, so $\bar v\in \bar {\mathbf {D}}$ . Set $\bar v'=(\bar g^{-1},\bar a^{-1},\bar x,\bar a,\bar g)$ . Then $\bar v'\in \bar {\mathbf {D}}$ and $\bar \Pi (\bar v')=\bar \Pi (\bar v)$ by $\bar {\mathbf {D}}$ -associativity. Thus

$$ \begin{align*}(\bar x^{\bar a})^{\bar g}=\bar x^{\bar a\bar g}=\bar x^{\bar g\bar b}=(\bar x^{\bar g})^{\bar b}\in\bar S. \end{align*} $$

This shows

(*) $$ \begin{align} (\bar P^{\bar a})^{\bar g}=\bar P^{\bar g\bar b}\leq\bar S. \end{align} $$

Thus, the set $\Gamma $ of all $\bar S_{\bar g}$ -conjugates of $\bar P$ is a set of subgroups of $\bar S$ contained in the set $\bar S_{\bar g}$ . Setting $X=\bigcup \Gamma $ , we thus have the setup of Lemma 4.2.

Assume now that $\bar P\neq \bar S_{\bar g}$ . Then Lemma 4.2 yields an element $\bar x\in \bar S_{\bar g}-\bar P$ such that $\bar x$ normalises $\bar P$ . Let Q be the $\beta $ -preimage of $\bar P\langle \bar x\rangle $ in S. Then $Q^g$ is defined (and is a subgroup of $N_{\mathcal {L}}(P^g)$ ) by Lemma 2.3(b). As $\bar Q^{\bar g}\leq \bar S$ , we obtain $Q^g\leq \mathcal {N}S$ . As $\mathcal {N}S$ is a locality by Lemma 4.1, it follows from Proposition 2.10(b) that there exists $f\in \mathcal {N}$ with $(Q^g)^f\leq S$ . Here $(g,f)\in \mathbf {D}$ via P, so $Q\leq S_{gf}$ , and this contradicts the $\uparrow $ -maximality of g. We conclude

1. (3) $(S_g)\beta =\bar S_{g\beta }$ for each $g\in \Lambda $ .

Thus (e) holds.

Next, let $w\in \mathbf {W}(\Lambda )$ , and define $\bar S_{\bar w}$ to be the set of all $\bar x\in \bar S$ such that $\bar x$ is conjugated successively into $\bar S$ by the entries of $\bar w$ . If w is not the empty word, then we may write $w=(g)\circ u$ for some $g\in \Lambda $ and $u\in \mathbf {W}(\Lambda )$ , and then $S_w=\{x\in S_g\mid x^g\in S_u\}$ . Then (3) together with induction on $\ell (w)$ yields

$$ \begin{align*}\bar{S_w}=\{\bar x\in\bar S_{\bar g}\mid \bar x^{\bar g}\in \bar S_{\bar u}\}=\bar S_{\bar w}. \end{align*} $$

Thus

1. (4) $(S_w)\beta =\bar S_{w\beta ^*}$ for all $w\in \mathbf {W}(\Lambda )$ .

We next verify that $(\bar {\mathcal {L}},\bar \Delta )$ is objective. Let $\mathbf {D}_{\bar {\Delta }}$ be the set of all $\bar w\in \mathbf {W}(\bar {\mathcal {L}})$ with $\bar S_{\bar w}\in \bar {\Delta }$ . Let $\bar w\in \mathbf {D}_{\bar {\Delta }}$ , and let $w\in \mathbf {W}(\Lambda )$ with $w\beta ^*=\bar w$ . We have $T\leq S_w$ by Proposition 3.9, and $T=S\cap Ker(\beta )$ , so $S_w$ is the $\beta _S$ -preimage of $(S_w)\beta $ . Then $S_w\in \Delta $ , so $w\in \mathbf {D}$ , and then (4) yields $\bar w\in \bar {\mathbf {D}}$ . Thus $\mathbf {D}_{\bar {\Delta }}\subseteq \bar {\mathbf {D}}$ . On the other hand, let $\bar v\in \bar {\mathbf {D}}$ , and let $v\in \mathbf {W}(\Lambda )$ with $v\beta ^*=\bar v$ . Then (b) yields $v\in \mathbf {D}$ , so $S_v\in \Delta $ , and $\bar v\in \mathbf {D}_{\bar {\Delta }}$ . Thus $\bar {\mathbf {D}}=\mathbf {D}_{\bar {\Delta }}$ , and $(\bar {\mathcal {L}},\bar \Delta )$ satisfies the condition (O1) in Definition 2.1 of objectivity.

Let $\bar P\in \bar {\Delta }$ , and let $\bar g\in \bar {\mathcal {L}}$ with $\bar P\leq \bar S_{\bar g}$ . Choose $g\in \Lambda $ with $g\beta =\bar g$ , and let P be the $\beta _S$ -preimage of $\bar P$ . Then $P\in \Delta $ , by the definition of $\bar {\Delta }$ , and we have $P\leq S_g$ by (3). Then $P^g\in \Delta $ , so $\bar P^{\bar g}\in \bar {\Delta }$ . All overgroups of $\bar P$ in $\bar S$ are in $\bar {\Delta }$ via the analogous property for P and S, so we have verified the condition (O2) in Definition 2.1. Thus $(\bar {\mathcal {L}},\bar \Delta )$ is objective.

To prove (c): Let $P,Q\in \Delta $ with $T\leq P\cap Q$ , set $\bar P=P\beta $ and $\bar Q=Q\beta $ , and let $\bar g\in \bar {\mathcal {L}}$ such that $\bar P^{\bar g}$ is defined and is a subset of $\bar Q$ . Let $g\in \Lambda $ be a preimage of $\bar g$ . Then $P\leq S_g$ by (4). As $\beta _S$ is a homomorphism, $(P^g)\beta =\bar P^{\bar g}$ is a subgroup of $\bar Q$ . Then $P^g\leq Q$ since $T=Ker(\beta _S)\leq P$ . That is, we have $g\in N_{\mathcal {L}}(P,Q)$ , and thus $\beta $ restricts to a surjection $\beta _{P,Q}:N_{\mathcal {L}}(P,Q)\to N_{\bar {\mathcal {L}}}(\bar P,\bar Q)$ . If $P=Q$ , then $\beta _{P,Q}$ is the homomorphism $\beta _P$ , so we have (c). Moreover, in the special case that $P=Q=S$ , we obtain in this way an epimorphism of $N_{\mathcal {L}}(S)$ onto $N_{\bar {\mathcal {L}}}(\bar S)$ . As S is a Sylow subgroup of $N_{\mathcal {L}}(S)$ , it follows that $\bar S$ is a Sylow p-subgroup of $N_{\bar {\mathcal {L}}}(\bar S)$ , whence $\bar S$ is a maximal p-subgroup of $\bar {\mathcal {L}}$ . Thus $(\bar {\mathcal {L}},\bar \Delta ,\bar S)$ is a locality.

To prove (a): Let $f\in \mathcal {L}$ , and let $h\in \Lambda $ with $f\beta =h\beta $ . By Proposition 3.14, there exists $g\in \Lambda $ with $f\in \mathcal {N}g$ , and then $f\beta =g\beta $ . Then $S_g=S_h$ by (3), so $(g,h^{-1})\in \mathbf {D}$ , and $(gh^{-1})\beta =\bar {\mathbf {1}}$ . Thus $gh^{-1}\in \mathcal {N}$ . As $(g,h^{-1},h)\in \mathbf {D}$ , we obtain $g\in \mathcal {N}h$ . Then $\mathcal {N}g=\mathcal {N}h$ by Proposition 3.14(d), and thus $f\in \mathcal {N}h$ . This yields (a), and it remains only to prove (d).

If $\beta $ is an isomorphism, then $\beta $ is injective, and $\mathcal {N}=\mathbf {1}$ . On the other hand, suppose that $\mathcal {N}=\mathbf {1}$ . Then (a) shows that $\beta $ is injective, so $\beta $ is a bijection, and $\mathbf {D}=\bar {\mathbf {D}}$ . Set $\gamma =\beta ^{-1}$ , and let $w\in \mathbf {D}$ . Then $w\gamma ^*\in \mathbf {D}$ as $\beta ^*$ is a bijection with inverse $\gamma ^*$ . We have $\Pi (w\gamma ^*)\beta =\Pi (w)$ since $\beta $ is a homomorphism, and thus $\Pi (w\gamma ^*)=(\Pi (w))\gamma $ . This shows that $\gamma $ is a homomorphism, so (d) holds, and the proof is complete.

Definition 4.4. Let $\mathcal {L}$ and $\mathcal {L}'$ be partial groups, and let $\beta :\mathcal {L}\to \mathcal {L}'$ be a homomorphism. Then $\beta $ is a projection if $\mathbf {D}(\mathcal {L})\beta ^*=\mathbf {D}(\mathcal {L}')$ .

Corollary 4.5. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $\mathcal {N}\trianglelefteq \mathcal {L}$ be a partial normal subgroup, and let $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ be the mapping that sends $g\in \mathcal {L}$ to the unique maximal coset of $\mathcal {N}$ containing g. Set $\bar {\mathcal {L}}=\mathcal {L}/\mathcal {N}$ , set $\bar S=S\rho $ , and let $\bar \Delta $ be the set of images under $\rho $ of the members of $\Delta $ . Regard $\bar {\mathcal {L}}$ as a partial group in the unique way (given by Lemma 3.16) that makes $\rho $ into a homomorphism of partial groups. Then $(\bar {\mathcal {L}},\bar \Delta ,\bar S)$ is a locality, and $\rho $ is a projection.

Proof. Immediate from Lemma 3.16 and Theorem 4.3.

Theorem 4.6 ‘First isomorphism theorem’

Let $(\mathcal {L},\Delta ,S)$ and $(\mathcal {L}',\Delta ',S')$ be localities, let $\beta :\mathcal {L}\to \mathcal {L}'$ be a projection, and let $\mathcal {N}\trianglelefteq \mathcal {L}$ be a partial normal subgroup of $\mathcal {L}$ contained in $Ker(\beta )$ . Let $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ be the projection given by Corollary 4.5. Then there exists a unique homomorphism

$$ \begin{align*}\gamma:\mathcal{L}/\mathcal{N}\to\mathcal{L}' \end{align*} $$

such that $\rho \circ \gamma =\beta $ , and then $\gamma $ is a projection. Moreover, we have $Ker(\gamma )=Ker(\beta )/\mathcal {N}$ , and $\gamma $ is an isomorphism if and only if $\mathcal {N}=Ker(\beta )$ .

Proof. Let $\Lambda (\mathcal {N})$ be the set of all $f\in \mathcal {L}$ such that f is $\uparrow $ -maximal relative to $\mathcal {N}$ . Set $\mathcal {M}=Ker(\beta )$ , and similarly define $\Lambda (\mathcal {M})$ . By Proposition 3.14(c), the maximal cosets of $\mathcal {N}$ in $\mathcal {L}$ are the sets $\mathcal {N}f$ with $f\in \Lambda (\mathcal {N})$ , and similarly for the maximal cosets of $\mathcal {M}$ . For any $g\in \mathcal {L}$ , we have $\mathcal {N}g\subseteq \mathcal {M}g$ as $\mathcal {N}\leq \mathcal {M}$ , so each maximal coset of $\mathcal {N}$ is contained in a maximal coset of $\mathcal {M}$ . Since the maximal cosets of $\mathcal {N}$ form the partition $\mathcal {L}/\mathcal {N}$ of $\mathcal {L}$ , it follows that each maximal coset of $\mathcal {M}$ is a union of maximal cosets of $\mathcal {N}$ . That is,

• (*) The partition $\mathcal {L}/\mathcal {N}$ of $\mathcal {L}$ is a refinement of the partition $\mathcal {L}/\mathcal {M}$ .

By Theorem 4.3(a), $\beta $ induces a bijection $\mathcal {L}/\mathcal {M}\to \mathcal {L}'$ . Set $\bar {\mathcal {L}}=\mathcal {L}/\mathcal {N}$ . Then (*) yields a mapping $\gamma :\bar {\mathcal {L}}\to \mathcal {L}'$ that sends the maximal coset $\mathcal {N}f$ to $f\beta $ . Clearly, $\gamma $ is the unique mapping $\bar {\mathcal {L}}\to \mathcal {L}'$ such that $\rho \circ \gamma =\beta $ .

Let $\bar w\in \mathbf {D}(\bar {\mathcal {L}})$ . Then Theorem 4.3(b) yields a word $w\in \mathbf {D}$ such that $w\rho ^*=\bar w$ and the entries of w are $\uparrow $ -maximal relative to $\mathcal {N}$ . We have $\bar w\gamma ^*=w\beta ^*$ , so $\gamma ^*$ maps $\mathbf {D}(\bar {\mathcal {L}})$ into $\mathbf {D}(\mathcal {L}')$ . Let $\Pi '$ and $\bar \Pi $ be the products in $\mathcal {L}'$ and $\bar {\mathcal {L}}$ , respectively. As $\beta $ and $\rho $ are homomorphisms, we get

$$ \begin{align*}\Pi'(\bar w\gamma^*)=\Pi'(w\beta^*)=(\Pi(w))\beta=(\bar{\Pi(w)})\gamma=(\bar\Pi(\bar w))\gamma, \end{align*} $$

and thus $\gamma $ is a homomorphism. As $\beta =\rho \circ \gamma $ is a projection, and since $\beta ^*=\rho ^*\circ \gamma ^*$ , $\gamma ^*$ maps $\mathbf {D}(\bar {\mathcal {L}})$ onto $\mathbf {D}(\mathcal {L}')$ . That is, $\gamma $ is a projection.

Clearly $\mathcal {M}/\mathcal {N}\leq Ker(\gamma )$ . On the other hand, if $\mathcal {N}f$ is a maximal coset of $\mathcal {N}$ with $\mathcal {N}f\in Ker(\gamma )$ , then $f\in Ker(\beta )$ , so $\mathcal {N}f\subseteq \mathcal {M}$ , and $\mathcal {N}f\in \mathcal {M}/\mathcal {N}$ . Thus $Ker(\gamma )=\mathcal {M}/\mathcal {N}$ . We have $\mathcal {M}=\mathcal {N}$ if and only if $Ker(\gamma )=\mathbf {1}$ . Then Theorem 4.3(d) shows that $\gamma $ is an isomorphism if and only if $\mathcal {M}=\mathcal {N}$ ; completing the proof.

Proposition 4.7 Partial subgroup correspondence

Let $(\mathcal {L},\Delta ,S)$ and $(\bar {\mathcal {L}},\bar \Delta ,\bar S)$ be localities, and let $\beta :\mathcal {L}\to \bar {\mathcal {L}}$ be a projection. Set $\mathcal {N}=Ker(\beta )$ , and set $T=S\cap \mathcal {N}$ . Then $\beta $ induces a bijection $\sigma $ from the set $\mathfrak {H}$ of partial subgroups $\mathcal {H}$ of $\mathcal {L}$ containing $\mathcal {N}$ to the set $\bar {\mathfrak {H}}$ of partial subgroups $\bar {\mathcal {H}}$ of $\bar {\mathcal {L}}$ . Moreover, for any $\mathcal {H}\in \mathfrak {H}$ , we have $\mathcal {H}\beta \trianglelefteq \mathcal {L}'$ if and only if $\mathcal {H}\trianglelefteq \mathcal {L}$ .

Proof. Any partial subgroup of $\mathcal {L}$ containing $\mathcal {N}$ is a union of maximal cosets of $\mathcal {N}$ by Lemma 3.15. Then Theorem 4.3(a) enables the same argument that one has for groups, for proving that $\rho $ induces a bijection $\mathfrak {H}\to \bar {\mathfrak {H}}$ . Since each maximal coset of $\mathcal {N}$ contains an element that is $\uparrow $ -maximal with respect to $\mathcal {N}$ , one may apply Theorem 4.3(b) to show that a partial subgroup $\mathcal {H}\in \mathfrak {H}$ is normal in $\mathcal {L}$ if and only if its image is normal in $\bar {\mathcal {L}}$ . The reader should have no difficulty with the details of the argument.

Remark 4.8. One may ask whether the ‘other two’ isomorphism theorems hold, in any sense, for localities. Let us formulate these for groups, rather than localities, as follows.

1. (1) Let G be a group, let $N\trianglelefteq G$ be a normal subgroup, and let $H\leq G$ be an arbitrary subgroup. Then the quotient map $G\to G/N$ restricts to an epimorphism $H\to HN/N$ with kernel $H\cap N$ .

2. (2) Let G be a group, let $N\trianglelefteq G$ be a normal subgroup, and let $K\trianglelefteq G$ with $N\leq K$ . Then the quotient map $G\to G/K$ factors through an epimorphism $G/N\to G/K$ with kernel $N/K$ .

A comprehensive version of (1) for localities appears to be out of reach for two reasons. First, given a partial subgroup $\mathcal {H}\leq \mathcal {L}$ and a partial normal subgroup $\mathcal {N}\trianglelefteq \mathcal {L}$ , there appears to be no reason for the image of $\mathcal {H}$ under the projection $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ to be a partial subgroup of $\mathcal {L}/\mathcal {N}$ , other than in special cases. Second, there seems to be no way, in general, to define the quotient of $\mathcal {H}$ over the partial normal subgroup $\mathcal {H}\cap \mathcal {N}$ of $\mathcal {H}$ .

On the other hand, one does indeed have the analogue of (2) for localities. Namely, let $\mathcal {L}$ be a locality, and let $\mathcal {N}\trianglelefteq \mathcal {L}$ and $\mathcal {K}\trianglelefteq \mathcal {L}$ be partial normal subgroups with $\mathcal {N}\leq \mathcal {K}$ . Then the projection $\mathcal {L}\to \mathcal {L}/\mathcal {K}$ factors through the projection $\mathcal {L}\to \mathcal {L}/\mathcal {N}$ by Theorem 4.6, yielding a projection $\mathcal {L}/\mathcal {N}\to \mathcal {L}/\mathcal {K}$ with kernel $\mathcal {N}/\mathcal {K}$ . (We shall not need this result, and we leave the details to the reader.)

Lemma 4.9. Let $\mathcal {N}\trianglelefteq \mathcal {L}$ , and let $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ be the canonical projection. Further, let $\mathcal {H}$ be a partial subgroup of $\mathcal {L}$ containing $\mathcal {N}$ , and let X be an arbitrary subset of $\mathcal {L}$ . Then $(X\cap \mathcal {H})\rho =X\rho \cap \mathcal {H}\rho $ .

Proof. By Lemma 3.15, $\mathcal {H}$ is a union of maximal cosets of $\mathcal {N}$ , and then $\mathcal {H}\rho $ is the set of those maximal cosets. On the other hand $X\rho $ is the set of all maximal cosets $\mathcal {N}g$ of $\mathcal {N}$ such that $X\cap \mathcal {N}g\neq \emptyset $ . Thus $X\rho \cap \mathcal {H}\rho \subseteq (X\cap \mathcal {H})\rho $ . The reverse inclusion is obvious.

Corollary 4.10. Let $\mathcal {N}\trianglelefteq \mathcal {L}$ , and let $\mathcal {M}$ be a partial normal subgroup of $\mathcal {L}$ containing $\mathcal {N}$ . Let $\rho :\mathcal {L}\to \mathcal {L}/\mathcal {N}$ be the canonical projection. Then $(S\cap \mathcal {M})\rho $ is a maximal p-subgroup of $\mathcal {M}\rho $ .

Proof. Write $(\bar {\mathcal {L}},\bar \Delta ,\bar S)$ for the quotient locality given by Corollary 4.5, and set $\bar {\mathcal {M}}=\mathcal {M}\rho $ . Applying Lemma 4.9 with S in the role of X, we obtain $(S\cap \mathcal {M})\rho =\bar S\cap \bar {\mathcal {M}}$ . Since $\bar {\mathcal {M}}\trianglelefteq \bar {\mathcal {L}}$ , it follows from Proposition 2.10(c) that $\bar S\cap \bar {\mathcal {M}}$ is maximal in the poset of p-subgroups of $\bar {\mathcal {M}}$ , completing the proof.

Proposition 4.11. Let $\mathcal {N}\trianglelefteq \mathcal {L}$ , set $T=S\cap \mathcal {N}$ , and set $\mathcal {L}_T=N_{\mathcal {L}}(T)$ . Set $\bar {\mathcal {L}}=\mathcal {L}/\mathcal {N}$ , and let $\rho :\mathcal {L}\to \bar {\mathcal {L}}$ be the canonical projection. Then the partial subgroup $\mathcal {L}_T$ of $\mathcal {L}$ is a locality $(\mathcal {L}_T,\Delta ,S)$ , and the restriction of $\rho $ to $\mathcal {L}_T$ is a projection $\mathcal {L}_T\to \bar {\mathcal {L}}$ .

Proof. That $\mathcal {L}_T$ is a partial subgroup of $\mathcal {L}$ having the structure of a locality $(\mathcal {L}_T,\Delta ,S)$ is given by Lemma 2.12. Let $\rho _T$ be the restriction of $\rho $ to $\mathcal {L}_T$ . Then $\rho _T$ is a homomorphism of partial groups, and Theorem 4.3(b) shows that $\rho _T$ maps $\mathbf {D}(\mathcal {L}_T)$ onto $\mathbf {D}(\bar {\mathcal {L}})$ . That is, $\rho _T$ is a projection.

We end this section with an application. For G a finite group, $O_{p'}(G)$ denotes the largest normal subgroup of G having order prime to p, and $O^p(G)$ is the smallest normal subgroup K of G such that $G/K$ is a p-group. Recall that, by definition, G is of characteristic p if $C_G(O_p(G))\leq O_p(G)$ . We assume that the reader is familiar with the definition of a fusion system over a finite p-group. For $(\mathcal {L},\Delta ,S)$ a locality one has the fusion system $\mathcal {F}_S(\mathcal {L})$ on S, whose isomorphisms are the conjugation maps $c_w$ (for $w\in \mathbf {W}(\mathcal {L})$ ) that were introduced following Definition 2.15.

Proposition 4.12. Let $(\mathcal {L},\Delta ,S)$ be a locality. For each $P\in \Delta $ set $\Theta (P)=O_{p'}(N_{\mathcal {L}}(P))$ , and set $\Theta =\bigcup \{\Theta (P)\}_{P\in \Delta }$ . Assume

• (*) $P\in \Delta \implies C_S(P)\leq P$ .

Then $\Theta \trianglelefteq \mathcal {L}$ , $S\cap \Theta =1$ , and the canonical projection $\rho :\mathcal {L}\to \mathcal {L}/\Theta $ restricts to an isomorphism $S\to S\rho $ . Moreover, upon identifying S with $S\rho $ ,

1. (a) $(\mathcal {L}/\Theta ,\Delta ,S)$ is a locality.

2. (b) $\mathcal {F}_S(\mathcal {L}/\Theta )=\mathcal {F}_S(\mathcal {L})$ .

3. (c) For each $P\in \Delta $ , the restriction

   $$ \begin{align*}\rho_P:N_{\mathcal{L}}(P)\to N_{\mathcal{L}/\Theta}(P) \end{align*} $$
   of $\rho $ induces an isomorphism
   $$ \begin{align*}N_{\mathcal{L}/\Theta}(P)\cong N_{\mathcal{L}}(P)/\Theta(P), \end{align*} $$
   and $N_{\mathcal {L}/\Theta }(P)$ is of characteristic p.

Proof. We first show

1. (1) For each $P\in \Delta $ , we have $C_{\mathcal {L}}(P)=Z(P)\times \Theta (P)$ .

Indeed, let $P\in \Delta $ . By Lemma 2.9, there exists $g\in \mathcal {L}$ with $P\leq S_g$ and such that $N_S(P^g)$ is a Sylow p-subgroup of $P^g$ . Set $Q=P^g$ . Then $Q\in \Delta $ , so $C_S(Q)\leq Q$ , and then $Z(Q)$ is a Sylow p-subgroup of $C_{\mathcal {L}}(Q)$ . Burnside’s theorem on normal p-complement’s (39.1 in [Asch], or 7.2.1 in [KS]) then yields $C_{\mathcal {L}}(Q)=Z(Q)\times \Theta (Q)$ , and then (1) follows from Lemma 2.3(b).

Next, let $x\in \Theta $ . Then there exists $Q\in \Delta $ with $x\in \Theta (Q)$ . Choose such a Q so that $|Q|$ is as large as possible, and set $R=N_{S_x}(Q)$ . Then $[R,x]\leq RR^x\leq S$ . But also

$$ \begin{align*}[R,x]\leq [N_{\mathcal{L}}(Q),\Theta(Q)]\leq\Theta(Q), \end{align*} $$

so $[R,x]=1$ , and then $x\in \Theta (R)$ by (1). The maximality of $|Q|$ then yields $Q=R$ . Thus $Q=S_x$ , and we have thus shown that $x\in \Theta (S_x)$ . Let $P\in \Delta $ with $P\leq S_x$ . Then x is a $p'$ -element of $C_{\mathcal {L}}(P)$ , so (1) yields $x\in \Theta (P)$ . Thus

1. (2) Let $x\in \Theta $ , and let $P\in \Delta $ with $P\leq S_x$ . Then $x\in \Theta (P)$ .

Clearly, $\mathbf {1}\in \Theta $ , and $\Theta $ is closed under inversion. Let

$$ \begin{align*}w=(x_1,\cdots,x_n)\in\mathbf{W}(\Theta)\cap\mathbf{D}, \end{align*} $$

and set $P=S_w$ . By (2), and by induction on n, we obtain $x_i\in \Theta (P)$ for all i, and hence $\Pi (w)\in \Theta (P)$ . Thus $\Theta $ is a partial subgroup of $\mathcal {L}$ . Now let $x\in \Theta $ , and let $g\in \mathcal {L}$ be given such that $(g^{-1},x,g)\in \mathbf {D}$ via some $Q\in \Delta $ . Then $Q^{g^{-1}}\leq S_x$ , so (2) yields $x\in \Theta (Q^{g^{-1}})$ , and then $x^g\in \Theta (Q)$ by Lemma 2.3(b). This completes the proof that $\Theta \trianglelefteq \mathcal {L}$ .

Set $\bar {\mathcal {L}}=\mathcal {L}/\Theta $ and adopt the usual ‘bar’-convention for images of elements, subgroups and collections of subgroups under the quotient map $\rho :\mathcal {L}\to \bar {\mathcal {L}}$ . Since $\Theta $ is a set of $p'$ -elements of $\mathcal {L}$ , we have $S\cap \Theta =\mathbf {1}$ , and we may therefore identify S with $\bar S$ and $\Delta $ with $\bar \Delta $ . Point (a) is then given by Corollary 4.5.

For each $P\in \Delta $ let $\rho _P$ be the restriction of $\rho $ to $N_{\mathcal {L}}(P)$ . Then $\rho _P$ is an epimorphism $N_{\mathcal {L}}(P)\to N_{\bar {\mathcal {L}}}(P)$ by Theorem 4.3(c), with kernel $\Theta (P)$ . This yields point (c).

By Theorem 4.3(c), the conjugation maps $c_g:P\to Q$ in $\mathcal {F}$ , with $P,Q\in \Delta $ and with $g\in \mathcal {L}$ , are the same as the conjugation maps $c_{\bar g}:P\to Q$ with $\bar g\in \mathcal {L}/\Theta $ . Since $\mathcal {F}_S(\mathcal {L})$ is $\Delta $ -generated (by Definition 2.11), we obtain $\mathcal {F}_S(\mathcal {L})=\mathcal {F}_S(\mathcal {L}/\Theta )$ . That is, (b) holds, and the proof is complete.

5 Products of partial normal subgroups

There are two main results in this section. The first (Theorem 5.1) concerns products of partial normal subgroups in a locality. The second (Proposition 5.5) is an application of essentially all of the results preceding it, and it will play a vital role in Part III of the series.

Theorem 5.1. Let $(\mathcal {L},\Delta ,S)$ be a locality, and let $\mathcal {M}\trianglelefteq \mathcal {L}$ and $\mathcal {N}\trianglelefteq \mathcal {L}$ be partial normal subgroups. Set $U=S\cap \mathcal {M}$ and $V=S\cap \mathcal {N}$ , and assume

• (*) $\mathcal {M}$ normalises V, and $\mathcal {N}$ normalises U.

Then $\mathcal {M}\mathcal {N}=\mathcal {N}\mathcal {M}\trianglelefteq \mathcal {L}$ , and $S\cap \mathcal {M}\mathcal {N}=UV$ .

The proof will require the following version of the splitting lemma (Lemma 3.12).

Lemma 5.2. Assume the hypothesis of Theorem 5.1, and let $g\in \mathcal {M}\mathcal {N}$ . Then there exists $(x,y)\in \mathbf {D}$ with $x\in \mathcal {M}$ , $y\in \mathcal {N}$ , $g=xy$ , and $S_g=S_{(x,y)}$ .

Proof. Consider the set of all triples $(g,x,y)\in \mathcal {M}\mathcal {N}\times \mathcal {M}\times \mathcal {N}$ such that g is a counterexample to the lemma and $g=xy$ . Among all such triples, let $(g,x,y)$ be chosen so that $|S_{(x,y)}|$ is as large as possible. Set $Q=S_{(x,y)}$ , and set $P=N_{S_g}(Q)$ . It suffices to show that $P=Q$ in order to obtain the lemma.

By Lemma 3.2, we have $(y,y^{-1},x,y)\in \mathbf {D}$ and $g=yx^y$ , with $S_{(x,y)}=S_{(y,x^y)}$ . Suppose that $P\leq S_y$ . Then $P^y\leq S$ , and since $P^g\leq S$ , we conclude that $P\leq S_{(y,x^y)}$ , and hence $P=Q$ , as desired. Thus we may assume

1. (1) $P\nleq S_y$ .

Let h be $\uparrow $ -maximal (with respect to $\mathcal {M}$ ) in the maximal coset of $\mathcal {M}$ containing g. By Proposition 3.14(c), there exists $r\in \mathcal {M}$ such that $g=rh$ , and Lemma 3.12 yields $S_g=S_{(r,h)}$ . Then $Q\leq S_{(r,h)}$ , so $(y^{-1},x^{-1},r,h)\in \mathbf {D}$ via $Q^g$ and $\Pi (y^{-1},x^{-1},r,h)=\Pi (g^{-1},g)=\mathbf {1}$ . Thus

(*) $$ \begin{align} h=r^{-1} xy \quad\text{and}\quad r^{-1} x=hy^{-1}. \end{align} $$

We have $y\in N_{\mathcal {L}}(U)$ by Theorem 5.1(*) and $h\in N_{\mathcal {L}}(U)$ by Proposition 3.9. Hence $r^{-1} x\in N_{\mathcal {M}}(U)$ , and then $h=(r^{-1} x)y\in \mathcal {M}\mathcal {N}$ .

Suppose that h does not provide a counterexample to the lemma. That is, suppose that there exists $x'\in \mathcal {M}$ and $y'\in \mathcal {N}$ such that $(x',y')\in \mathbf {D}$ , $x'y'=h$ , and $S_{(x',y')}=S_h$ . As $r^{-1} xy=h=x'y'$ , we get $xy=rx'y'$ , and $(r,x',y')\in \mathbf {D}$ with $rx'y'=rh=g$ . The idea now is to replace $(x,y)$ with $(rx',y')$ and contradict the assumption that $S_g\neq Q$ . To achieve this, observe first that $S_g\leq S_r$ since $S_{(r,h)}=S_{rh}=S_g$ . Then observe that $(S_g)^r\leq S_h$ and $S_h=S_{(x',y')}\leq S_{x'}$ . Thus $(S_g)^r\leq S_{x'}$ , so $S_g\leq S_{rx'}$ . As $rx'y'=g$ , we conclude that $S_g\leq S_{(rx',y')}$ , which yields the desired contradiction. We conclude that h is itself a counterexample to the lemma.

Recall that we have $r^{-1} x\in N_{\mathcal {M}}(U)$ . Then $U\leq S_{(r^{-1} x,y)}$ since $h\in N_{\mathcal {L}}(U)$ . Note furthermore that $Q=S_{(x,y)}\leq S_g=S_{(r,h)}\leq S_r$ , and thus $Q^rU\leq S_{(r^{-1} x,y)}$ . The maximality of $|Q|$ in our initial choice of $(g,x,y)$ then yields $Q^r=Q^rU=S_{(r^{-1} x,y)}$ . Thus $U^r\leq Q^r$ , and conjugation by $r^{-1}$ yields $U\leq Q$ . A symmetric argument yields $V\leq Q$ . Setting $H=N_{\mathcal {L}}(Q)$ , it now follows from Lemma 3.1(b) that $x,y\in H$ .

Set $X=H\cap \mathcal {M}$ and $Y=H\cap \mathcal {N}$ . Then $X,Y$ and $UV$ are normal subgroups of H, and $XY/UV$ is a $p'$ -group. Set $\bar H=H/(X\cap Y)UV$ . Here $P\leq H$ and $[P,g]\leq S$ . Since $g\in XY$ , we obtain

$$ \begin{align*}[\bar P,\bar g]=[\bar P,\bar x\bar y]\leq \bar X\bar Y, \end{align*} $$

and since $\bar X\bar Y$ is a $p'$ -group we get $[\bar P,\bar g]=1$ . As $\bar X\cap \bar Y=1$ , we have $C_{\bar X\bar Y}(\bar P)=C_{\bar X}(\bar P)\times C_{\bar Y}(\bar P)$ . As $\bar g=\bar x\bar y$ , it follows that $\bar x$ and $\bar y$ centralise $\bar P$ . Thus $P^x\leq (X\cap Y)P$ and $P\in Syl_p((X\cap Y)P)$ . By Sylow’s theorem, there exists $z\in X\cap Y$ with $P^x=P^z$ . We then get $g=(xz^{-1})(zy)$ and $P\leq S_{(xz^{-1},zy)}$ . This contradicts the maximality of Q and yields a final contradiction, proving the lemma.

Proof of Theorem 5.1

Let $w=(g_1,\cdots ,g_n)\in \mathbf {W}(\mathcal {M}\mathcal {N})\cap \mathbf {D}$ via $Q\in \Delta $ . By Lemma 5.2, we may write $g_i=x_iy_i$ with $x_i\in \mathcal {M}$ , $y_i\in \mathcal {N}$ , and with $S_{g_i}=S_{(x_i,y_i)}$ . Set $w'=(x_1,y_1,\cdots ,x_n,y_n)$ . Then $w'\in \mathbf {D}$ via Q and $\Pi (w)=\Pi (w')$ . Since each $y_i$ normalises U, it follows from Lemma 3.4 that $\Pi (w')=\Pi (w'')$ for some $w''\in \mathbf {D}$ such that $w''=(x)\circ (y_1,\cdots ,y_n))$ , where $x\in \mathcal {M}$ . Thus $\mathcal {M}\mathcal {N}$ is closed under $\Pi $ . To show that $\mathcal {M}\mathcal {N}=(\mathcal {M}\mathcal {N})^{-1}$ , we note that if $(x,y)\in \mathbf {D}\cap (\mathcal {M}\times \mathcal {N})$ , then $(y^{-1},x^{-1})\in \mathbf {D}$ , and that $y^{-1} x^{-1}\in \mathcal {M}\mathcal {N}$ by Lemma 3.2. Thus $\mathcal {M}\mathcal {N}$ is a partial subgroup of $\mathcal {L}$ . Moreover, we have shown that $\mathcal {M}\mathcal {N}=\mathcal {N}\mathcal {M}$ .

Let $g\in \mathcal {M}\mathcal {N}$ , and let $f\in \mathcal {L}$ with $(f^{-1},g,f)\in \mathbf {D}$ . By Lemma 3.12, we may write $f=hr$ with $r\in \mathcal {N}$ , $h\in N_{\mathcal {L}}(V)$ and $S_f=S_{(h,r)}$ . Write $g=xy$ as in Lemma 5.2. By assumption, we have $(f^{-1},g,f)\in \mathbf {D}$ via some $P\in \Delta $ . Setting $v=(r^{-1},h^{-1},x,y,h,r)$ , it follows that $v\in \mathbf {D}$ via P and $g^f=\Pi (v)$ . Here $(h^{-1},h,y,h)\in \mathbf {D}$ via $S_{(y,h)}$ by Lemma 3.2, so $v':=(r^{-1},h^{-1},x,h,h^{-1},y,h,r)\in \mathbf {D}$ via P. Then

$$ \begin{align*}g^f=\Pi(v)=\Pi(v')=(x^h y^h)^r\in(\mathcal{M}\mathcal{N})^r. \end{align*} $$

Since $r\in \mathcal {N}$ and $\mathcal {M}\mathcal {N}$ is a partial group, we conclude that $g^f\in \mathcal {M}\mathcal {N}$ . Thus $\mathcal {M}\mathcal {N}\trianglelefteq \mathcal {L}$ .

Set $M=N_{\mathcal {M}}(S)$ , $N=N_{\mathcal {N}}(S)$ , and let $s\in S\cap \mathcal {M}\mathcal {N}$ . Then Lemma 5.2 yields $s=fg$ with $f\in \mathcal {M}$ , $g\in \mathcal {N}$ and with $S=S_{(f,g)}$ . Thus $f\in M$ and $g\in N$ , where M and N are normal subgroups of the group $N_{\mathcal {L}}(S)$ . Then $UV$ is a normal Sylow p-subgroup of $MN$ , and since $s=fg\in MN$ , we obtain $s\in UV$ . Thus $S\cap \mathcal {M}\mathcal {N}=UV$ , and the proof is complete. $ \Box $

Lemma 5.3. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $\mathcal {M}$ and $\mathcal {N}$ be partial normal subgroups of $\mathcal {L}$ , and set $U=S\cap \mathcal {M}$ and $V=S\cap \mathcal {N}$ . Suppose that $\mathcal {M}\cap \mathcal {N}\leq S$ . Then $\mathcal {M}\leq N_{\mathcal {L}}(V)$ and $\mathcal {N}\leq N_{\mathcal {L}}(U)$ .

Proof. Let $g\in \mathcal {M}$ , set $P=S_g$ , and let $x\in N_V(P)$ . Then $(x^{-1},g^{-1},x,g)\in \mathbf {D}$ via $P^{gx}$ , and then $x^{-1} g^{-1} xg\in \mathcal {M}\cap \mathcal {N}$ . The hypothesis then yields $x^g\in S$ , and thus $N_V(P)\leq P$ . Since $PV$ is a subgroup of S, we conclude that $V\leq P$ , and then $V^g=V$ by Lemma 3.1(a). Thus $\mathcal {M} \leq N_{\mathcal {L}}(V)$ , and a symmetric argument shows that $\mathcal {N}\leq N_{\mathcal {L}}(U)$ .

Corollary 5.4. Let $\mathcal {M},\mathcal {N}\trianglelefteq \mathcal {L}$ and suppose that $\mathcal {M}\cap \mathcal {N}\leq S$ . Then $\mathcal {M}\mathcal {N}\trianglelefteq \mathcal {L}$ , and $S\cap \mathcal {M}\mathcal {N}=(S\cap \mathcal {M})(S\cap \mathcal {N})$ .

Proof. Immediate from Theorem 5.1 and Lemma 5.3.

Recall that a finite group G is of characteristic p if $C_G(O_p(G))\leq O_p(G)$ .

Proposition 5.5. Let $(\mathcal {L},\Delta ,S)$ be a locality, let $\mathcal {N}\trianglelefteq \mathcal {L}$ be a partial normal subgroup, set $T=S\cap \mathcal {N}$ , set $\mathcal {L}_T=N_{\mathcal {L}}(T)$ , and let $\mathcal {K}$ be a partial normal subgroup of $\mathcal {L}_T$ . Assume

1. (1) Each of the groups $N_{\mathcal {L}}(P)$ for $P\in \Delta $ is of characteristic p, and

2. (2) $\mathcal {K}\leq C_{\mathcal {L}}(T)$ .

Then $\langle \mathcal {K},\mathcal {N}\,\rangle \trianglelefteq \mathcal {L}$ , and $S\cap \langle \mathcal {K},\mathcal {N}\,\rangle =(S\cap \mathcal {K})T$ . Moreover, if $S=C_S(T)T$ , then $\langle \mathcal {K},\mathcal {N}\,\rangle =\mathcal {K}\mathcal {N}=\mathcal {N}\mathcal {K}$ .

Proof. Set $\mathcal {N}_T=N_{\mathcal {N}}(T)$ . Then $\mathcal {N}_T\trianglelefteq \mathcal {L}_T$ by Lemma 1.8. View $\mathcal {L}_T$ as a locality $(\mathcal {L}_T,\Delta ,S)$ as in Lemma 2.12. The condition (1) allows us to apply Lemma 3.7 and thereby conclude that $\mathcal {N}_T$ normalises $C_S(T)T$ . Set $U=S\cap \mathcal {K}$ . Then $U\leq C_S(T)$ by (2), and then $[U,\mathcal {N}_T]\leq C_S(T)T\cap \mathcal {K}=U$ . Thus $\mathcal {N}_T$ normalises U. Since $\mathcal {K}$ normalises T, we conclude from Theorem 5.1 that $\mathcal {K}\mathcal {N}_T\trianglelefteq \mathcal {L}_T$ .

Let $\bar {\mathcal {L}}$ be the quotient locality $\mathcal {L}/\mathcal {N}$ , and let $\rho :\mathcal {L}\to \bar {\mathcal {L}}$ be the canonical projection. Then the restriction of $\rho $ to $\mathcal {L}_T$ is a projection $\mathcal {L}_T\to \bar {\mathcal {L}}$ by Proposition 4.11, and $(\mathcal {K}\mathcal {N}_T)\rho =\mathcal {K}\rho $ . Then $\mathcal {K}\rho \trianglelefteq \bar {\mathcal {L}}$ by partial subgroup correspondence (Proposition 4.7). The $\rho $ -preimage of $\mathcal {K}\rho $ in $\mathcal {L}$ is then a partial normal subgroup of $\mathcal {L}$ containing the partial subgroup $\langle \mathcal {K},\mathcal {N}\,\rangle $ of $\mathcal {L}$ generated by $\mathcal {K}$ and $\mathcal {N}$ .

By Lemma 1.9, $\langle \mathcal {K},\mathcal {N}\,\rangle $ is the union of its subsets $Y_i$ , where $Y_0=\mathcal {K}\cup \mathcal {N}$ and (for $k>0$ ) $Y_k$ is the set of all $\Pi (w)$ with $w\in \mathbf {W}(Y_{k-1})\cap \mathbf {D}$ . Clearly $\rho $ maps $Y_0$ into $\mathcal {K}\rho $ , and a straightforward induction on k then shows that $\rho $ maps each $Y_k$ into $\mathcal {K}\rho $ . Thus $\langle \mathcal {K},\mathcal {N}\,\rangle $ is mapped onto $\mathcal {K}\rho $ , and partial subgroup correspondence then implies that $\langle \mathcal {K},\mathcal {N}\,\rangle $ is the preimage of $\mathcal {K}\rho $ . As $\mathcal {K}\rho \trianglelefteq \bar {\mathcal {L}}$ , a further application of partial subgroup correspondence yields $\langle \mathcal {K},\mathcal {N}\,\rangle \trianglelefteq \mathcal {L}$ .

Set $U=S\cap \mathcal {K}$ , and set $V=S\cap \langle \mathcal {K},\mathcal {N}\,\rangle $ . Then the restriction of $\rho $ to V is a homomorphism of groups by Lemma 1.16, with kernel T. Here U is a maximal p-subgroup of $\mathcal {K}$ by Lemma 3.1(c), and both $V\rho $ and $U\rho $ are maximal p-subgroups of $\mathcal {K}\rho $ by Corollary 4.10. Then $V\rho =U\rho $ and $V=UT$ .

Suppose now that $S=C_S(T)T$ . Then each element of $\mathcal {K}$ is $\uparrow $ -maximal with respect to $\mathcal {N}$ , by Lemma 3.10. Let $w\in \mathbf {W}(\mathcal {K}\mathcal {N})\cap \mathbf {D}$ , write $w=(x_1y_1,\cdots ,x_ny_n)$ with $x_i\in \mathcal {K}$ and $y_i\in \mathcal {N}$ , and set $w'=(x_1,y_1,\cdots ,x_n,y_n)$ . Then $w'\in \mathbf {D}$ by the splitting lemma (Lemma 3.12), and $\Pi (w)=\Pi (w')$ . Here $\Pi (w')\in \mathcal {K}\mathcal {N}$ by Lemma 3.4, so $\langle \mathcal {K},\mathcal {N}\,\rangle =\mathcal {K}\mathcal {N}$ in this case. One similarly has $\langle \mathcal {K},\mathcal {N}\,\rangle =\mathcal {N}\mathcal {K}$ , completing the proof.

Remark 5.6. In the proof of Proposition 5.5, hypothesis (2) serves no other purpose than to guarantee that $\mathcal {K}\mathcal {N}_T$ is a partial normal subgroup of $\mathcal {L}_T$ . In fact, by [He, Theorem A in], the product of partial normal subgroups of a locality is always a partial normal subgroup, so (2) is redundant.