Gini coefficients are not inherently a measure of wealth inequality; they are actually a measure of unevenness in the distribution across a population of whatever observations the coefficients are based on. (Peterson and Drennan Reference Peterson, Drennan, Kohler and Smith2018:39)
This article introduces Ancient Mesoamerica's first Compact Special Section—a new format where the first article presents theoretical and methodological background on a topic so that the following articles can focus on specific sets of data and integrated research problems. This Compact Special Section addresses residential inequality in Classic Maya (a.d. 250–900) cities, with this introduction providing sections including: a background to how inequality has been studied; overviews of the Gini coefficient and Lorenz curve; details on three prior comparative models of inequality; multiple ways to measure inequality from residential size; a case study with data from the city of Caracol in modern Belize; summaries for the articles included in this section; preliminary results from this research; and then a final valediction. In aggregate, this Compact Special Section (along with the associated tools and code provided in the supplementary materials) helps to democratize these methods while providing the necessary background to avoid misuse. Although the topic of inequality is much larger than just the Gini (as we discuss in the following pages), it provides a quintessential tool for comparative research.
Analysis of inequality—and use of the Gini coefficient—has remained a pertinent topic of scholarly interest for well over a century (Gini Reference Gini1912); however, a multitude of ways to measure and consider disparities among peoples, households, and places exist, from various quality of life and capability metrics (e.g., Arponen et al. Reference Arponen, Müller, Hofmann, Furholt, Ribeiro, Horn and Hinz2016; Borgerhoff Mulder et al. Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009; Bourdieu Reference Bourdieu and Richardson1986; Bowles et al. Reference Bowles, Smith and Mulder2010; Guyer Reference Guyer1993, Reference Guyer1995; Guyer and Belinga Reference Guyer and Eno Belinga1995; Munson and Scholnick Reference Munson and Scholnick2022; Nussbaum and Sen Reference Nussbaum and Sen1993; Phillips Reference Phillips2006; Sen Reference Sen1973, Reference Sen1992, Reference Sen1999) to aggregated indices and modified methodological approaches (see, e.g., Blesch et al. Reference Blesch, Hauser and Jachimowicz2022; Bowles and Carlin Reference Bowles and Carlin2020; Neves Costa and Pérez-Duarte Reference Neves Costa and Pérez-Duarte2019; Oka et al. Reference Oka, Ames, Chesson, Kuijt, Kusimba, Gogte, Dandekar, Kohler and Smith2018; Sitthiyot and Holasut Reference Sitthiyot and Holasut2020). Separate critiques of composite measures like Gini also exist, focusing on how such metrics mix inequalities resulting from income as resource flows and capital as assets (Piketty Reference Piketty2014)—at least in the modern and historic datasets used. Despite these, the most common method used in (and outside of) archaeology today for comparative analyses of inequality (regardless of what is measured) continues to be the Gini coefficient and its associated graphical representation in the Lorenz curve. Here, we provide the background and methods to avoid common pitfalls in using Gini to assess inequality.
Although different sets of information can be used to calculate a Gini and measure inequality (as unevenness in a distribution of some measurable thing), archaeological applications of Gini often focus on the sizes of residences, given the more permanent nature of these features in the built environment. Even so, multiple definitions of residential size have been measured and compared, potentially leading to inaccurate conclusions. In this Compact Special Section, we offer three standardized methods for measuring and comparing residences: (1) open-source tools for common methods of calculating and analyzing Gini, Lorenz curves, and additional statistics; (2) theoretical models and considerations for comparative analysis; (3) and a brief overview of multiple case studies, with aggregated results based on nearly two dozen Maya centers (Figure 1).

Figure 1. Map of the Maya region, showing the locations of the Classic Maya (a.d. 250–900) centers analyzed in this Compact Special Section. Map by Amy Thompson.
We emphasize that comparative data on inequality must be based on standardized and consistent units of analysis and analytical parameters. That is, it is essential to compare “like with like” and avoid comparisons of area with volume and individual structures with entire households of roofed and unroofed areas. Drawing on our preliminary results, we suggest that at the largest cities in this sample, inequality-reducing practices were employed. Interestingly, the distributions of area and volume measures from these analyses align with the expected range of inequalities for total (income and capital) inequality (0.3, 0.5) and capital ownership (0.6, 0.9), respectively, as outlined by Piketty (Reference Piketty2014:266–267) for historic and modern populations—an analytical parallel that requires future research.
Scholars have defined residential size in multiple ways and for a variety of purposes over the last several decades. Although Brown (Reference Brown1987) and Naroll (Reference Naroll1962) focused on house size as a means to estimate past populations, current practices in archaeology also view house size as a key representation of accumulated domestic wealth (e.g., Basri and Lawrence Reference Basri and Lawrence2020; Kohler and Smith Reference Kohler and Smith2018). These perspectives are synergistic because larger residences would accommodate additional inhabitants; and those residents and their aggregated daily labor, contacts beyond the household, and personal knowledge would have provided forms of wealth for the household as a whole.
Here we focus on six standardized measures of residential-level inequality based on house-size. For the parameters to analyze, we measure area (m2) and volume (m3) for three definitions of residential unit: entire “plazuela groups” (Thompson Reference Thompson1931:233), also called “patio groups” (Ashmore Reference Ashmore and Ashmore1981:48–49), aggregated physical structures in the group providing just the “roofed areas” of a Plazuela; and individual mounds and structures—often with constraints to remove non-residential structures (see Thompson et al. Reference Thompson, Feinman and Prufer2021a, Reference Thompson, Chase and Feinman2023). As described in more detail by Thompson and co-authors (Reference Thompson, Chase and Feinman2023), the above creates six metrics by combining three household definitions (residential units of analysis) and the distinctions between area and volume metrics (analytical parameters). Direct comparisons of inequality require consistent use of the same metric (to compare like with like), and standardized definitions of residences are employed to accomplish this. Previous scholarship has combined multiple definitions of house size into singular analyses, even within the same cultural region, leading to potentially inaccurate views of past inequality (e.g., initial results in Kohler et al. Reference Kohler, Smith, Bogaard, Feinman, Peterson, Betzenhauser, Pailes, Stone, Prentiss, Dennehy, Ellyson, Nicholas, Faulseit, Styring, Whitlam, Fochesato, Foor and Bowles2017, with data and analysis issues mentioned in Chase Reference Chase, Kohler and Smith2019).
By providing accessible methods and comparative data, this Compact Special Section aims to help democratize analysis of inequality through the calculating files and code provided in the supplementary materials. In addition, these methods and tools may be used for any quantifiable datasets; if researchers want to investigate other types of inequality (or “disparity,” if perception of inequality is unclear following Munson and Scholnick Reference Munson and Scholnick2022:16–17) using Gini, Lorenz curves, and other metrics, they can use the methods, code, and tools provided here. These tools are not limited to house size measurements. However, the limitations on comparing “like with like” means that large-scale, collaborative work will be required for investigation of inequality across regions (see also Kohler and Thompson Reference Kohler and Thompson2022). Fundamentally, this Compact Special Section provides the concepts, theory, and tools needed as a starting point to pursue similar investigations in any spatiotemporal context.
Theories of inequality
Inequality—of multiple forms—is extant in modern societies, was present in historic and prehistoric societies, and even exists among “egalitarian” societies (see Flanagan Reference Flanagan1989). However, the form and perceptions of inequality, and their manifestations, differ between spatiotemporal contexts. This means that we can discuss relative inequality between the past and present, but we need to remain aware of potential differences through time and perception by people at those times. Inequality exists in multiple forms, including variations on social status, power and authority, relationships, and wealth (the focus of this Compact Special Section's datasets). When considering wealth inequality, there are three generalized fundamental types: material, relational, and embodied (see Borgerhoff Mulder et al. Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009; Bowles et al. Reference Bowles, Smith and Mulder2010) These also match Bourdieu's (Reference Bourdieu and Richardson1986) concepts of economic capital, social capital, and cultural capital respectively, and provide a useful distinction for looking at other forms of inequality.
Material inequality refers to physical objects and goods (Bowles et al. Reference Bowles, Smith and Mulder2010:9–10), and it is the most frequent type measured by archaeologists given the nature of archaeological data as collections of portable artifacts (such as ceramic vessels, stone tools, or jade beads) and the sizes of stationary features (such as houses, graves, or storage areas). In essence, this is the tangible, physical manifestation of inequality and is measurable through accrued things, places, and objects. Archaeological measures often include house size (see, e.g., Ames and Grier Reference Ames and Grier2020; Basri and Lawrence Reference Basri and Lawrence2020; Feinman and Nicholas Reference Feinman, Nicholas, Bussman and Helms2020; Hutson and Welch Reference Hutson and Welch2021; Strawinska-Zanko et al. Reference Strawinska-Zanko, Liebovitch, Watson, Brown, Strawinska-Zanko and Liebovitch2018), as we use here, or specific objects and materials recovered along with some way to translate those into wealth (e.g., Drennan et al. Reference Drennan, Peterson, Fox, Douglas Price and Feinman2010; Peterson and Drennan Reference Peterson, Drennan, Kohler and Smith2018; Smith Reference Smith1987). Modern measures of wealth (e.g., not including archaeological data) instead tend to focus on income and capital disparities, where income includes resource flows and capital includes stocks and assets (Piketty Reference Piketty2014:50–52). This distinction yields different values under analysis (for example, someone with many stocks and assets can be wealthy without a salaried income), but would be difficult or potentially impossible to reconstruct archaeologically from contexts lacking historical tax records (Piketty Reference Piketty2014:17, 266–267).
Relational inequality refers to the network positioning and physical ties of the individual being measured (Bowles et al. Reference Bowles, Smith and Mulder2010:9–10). These types of structured relationships have been a frequent topic of both anthropological and archaeological inquiries (Goodenough Reference Goodenough and Banton1965; Linton Reference Linton1936:113–131; Sabloff and Cragg Reference Sabloff, Cragg, Sabloff and Sabloff2018), with implications on social wealth, position, and statuses. An individual's relative positioning in society applies especially to social and political inequalities, and reflects an individual's position in a network. These archaeological concepts integrate well with existing social network analysis perspectives more broadly, and specifically with definitions of “network centrality” that provide several interpretations and measurements of the comparative positioning of specific nodes in networks (see Borgatti Reference Borgatti2005; Rivers et al. Reference Rivers, Knappett, Evans and Knappett2013). For a pertinent modern example, Oka and colleagues (Reference Oka, Ames, Chesson, Kuijt, Kusimba, Gogte, Dandekar, Kohler and Smith2018:71–73) present the idea that wealth inequalities in the Soviet Union remained more visible in access to services, a form of relational wealth, rather than in variation among house sizes, a form of material wealth. This suggests that relational wealth may also be considered in terms of time, space, and access to resources on physical landscapes in addition to social connections, statuses, and positions of individuals.
Embodied inequality refers to inseparable aspects of an individual, such as their skills, knowledge, or physical characteristics. This category provides a means of looking at the intrinsic qualities of an individual that lead to inequalities in contrast to relational and material forms, which are both extrinsic. Archaeologically, this is the most challenging form of wealth to assess—especially at larger scales—and specific aspects remain debated. For example, dental modification among the ancient Maya has been argued to represent a form of embodied wealth by Munson and Scholnick (Reference Munson and Scholnick2022:15), but Tiesler (Reference Tiesler, Hutson and Ardren2020:114) argues that no patterns exist to indicate that dental modification went beyond personal or familial choices (something also noted at Caracol; see Chase Reference Chase2023). This type of wealth focuses on individuals and their personal characteristics to such a degree that it may not be an applicable form of inequality to apply to residences as a whole. More modern views of embodied wealth would include the “personal assets” of an individual (e.g., Hakim Reference Hakim2010).
Beyond these three types of wealth—which can be studied economically, politically, socially, and so on—two additional factors should be considered: the scale of analysis and emic perceptions of wealth and inequality. First, the levels of analysis can differ (see Chase Reference Chase, Cervantes and Walden2024). While we can investigate inequality at the individual or household level, they generate incomparable Gini metrics and provide different perspectives on the nature of disparity. In other words, comparisons within or between households yield different perspectives on inequality and society than those between people. Also, depending on the research question at hand, it may be reasonable to aggregate at different scales for comparative purposes. Second, emic or indigenous perspectives on wealth as inequality should be considered. What we, from an etic perspective, use to define material, economic “inequality” between residents or households, such as differences in construction materials, size, or location, may not have been emically perceived as markers of inequality by ancient or modern peoples (e.g., Wilk Reference Wilk1983:103–104).
Munson and Scholnick (Reference Munson and Scholnick2022:16–17) use the term “disparity” to distinguish between inequality from material remains (that are easier to perceive archaeologically) and disparities that arise between relational and embodied forms of wealth (that are harder to perceive archaeologically); Peterson and Drennan (Reference Peterson, Drennan, Kohler and Smith2018) use the term “differentiation” for all three wealth types instead. In some instances, variability in metrics of wealth may reflect scalar or categorical discrepancies in political power or the degree of social control (see Shaw-Müller and Walden Reference Shaw-Müller and Walden2023; Walden et al. Reference Walden, Hoggarth, Ebert, Shaw-Müller, Weiyu, Yijia, Ellis, Meyer, Biggie, Watkins, Guerra and Awe2023). Both terms—disparity and differentiation—encapsulate the issue of difference in perceptions of wealth that may not directly translate to inequality and facilitate using these analyses for non-economic types of inequality. By measuring variability in multiple metrics—which potentially relate to inequality—we might be better able to identify how, and if, these factors overlap and which ones are more likely to emically reflect perceived differences by people in the past. In addition, absolute wealth does not directly map onto the capability of a person to enjoy a good life (e.g., Nussbaum and Sen Reference Nussbaum and Sen1993; Sen 1972, Reference Sen1992, Reference Sen1999). Although capabilities may be more difficult to ascertain archaeologically, the archaeological record alone has the potential to reveal the full diversity of wealth, equality, and inequality that has been experienced by people throughout history. In this Compact Special Section, we focus on residential size within each center (i.e., settlement or site; see Thompson et al. Reference Thompson, Walden, Chase, Hutson, Marken, Cap, Fries, Piedrasanta, Hare, Horn, Micheletti, Montgomery, Munson, Richards-Rissetto, Shaw-Müller, Ardren, Awe, Kathryn Brown, Callaghan, Ebert, Ford, Guerra, Hoggarth, Kovacevich, Morris, Moyes, Powis, Yaeger, Houk, Prufer, Chase and Chase2022:5) as a form of wealth, assuming that differences in house size were perceived as a form of economic inequality by their residents (see also Basri and Lawrence Reference Basri and Lawrence2020:690–691).
Taken together material, relational, and embodied wealth can be analyzed in multiple ways that facilitate thinking about “wealth” as inequality, disparity, or differentiation among some measurable quantity. This framework also firmly establishes multiple perspectives for investigating these concepts throughout human history, and that future research can incorporate others.
The Gini coefficient and Lorenz curve
Measures of inequality can be implemented through a variety of calculations, including the Gini coefficient. A Gini can range from 0 to 1, where a value of 0 represents perfect equality and 1 represents perfect inequality (Gini Reference Gini1912). Although the Gini is often used to measure wealth inequalities, it is actually just a measure of the unevenness of a batch of the input variable that the coefficient is based on (Peterson and Drennan Reference Peterson, Drennan, Kohler and Smith2018:39). This concept of inequality as unevenness matches measures of inequality (i.e., if everything is even, then everything is equal), and follows from the mathematical nature of the problem as one of comparative area measurements (i.e., calculus) that can be visualized. The Lorenz curve is a graphical perspective of a Gini (Gastwirth Reference Gastwirth1972), and combined they provide complementary methods to investigate the distribution in the units being measured—in this case, house size. Standard descriptive statistics should also be reported, including minimum, maximum, range, median, mean, standard deviation, and coefficient of variation, as they provide useful insights for our interpretations of inequality and help surpass some basic issues—especially since the Gini presents us with one simplification about differences within a distribution and not about these other aspects of the distribution itself.
Modern critiques of these and other composite metrics primarily focus on what is being measured, like Piketty's (Reference Piketty2014:266–267) distinction between capital and labor or, as demonstrated by Blesch and colleagues (Reference Blesch, Hauser and Jachimowicz2022), how multiple metrics provide a more complete perspective. The first matters because different forms of wealth have different expected Gini for distributions of labor income (0.2–0.4), capital ownership (0.6–0.9), and total inequality (0.3–0.5), as mentioned by Piketty (Reference Piketty2014:266–267) in modern and historic datasets. The latter matters because inequality can be rendered less, or more, visible in one type of measurement than in another (e.g., Borgerhoff Mulder et al. Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009; Munson et al. Reference Munson, Scholnick, Ramón and Aragon2023; Oka et al. Reference Oka, Ames, Chesson, Kuijt, Kusimba, Gogte, Dandekar, Kohler and Smith2018:71–73). In essence, multiple scholars have updated and modified the Gini index, but their results have simply shifted the underlying analytical issues. As Neves Costa and Pérez-Duarte (Reference Neves Costa and Pérez-Duarte2019:47) point out, “All these different measures are, however, sensitive to different parts of the distribution and can lead to different measures of changes—over time or over space.” Despite all the proposed alternatives, the common use of the Gini coefficient and Lorenz curve persists because researchers from multiple fields can easily calculate and understand the comparative implications of these measures. This does not negate the flaws of the Gini coefficient that inevitably arise from any simplification of more complex data, but it does demonstrate its overall utility despite those issues. Fundamentally, these measures of inequality provide two of many potential tools to describe distributions and can be used in conjunction with others—or with multiple datasets—for additional insights.
The Lorenz curve provides a way to visualize a Gini. The “line of equality” in the Lorenz curve provides the baseline of y = x, where each additional person owns an equal percentage of the unit being measured (e.g., income, residential size, ceramic vessels). This is contrasted with the line showing the actual percentage of ownership against that percentage of the population. In both, the lines start at the origin because 0 percent of people always own 0 percent of the unit being measured, and they always end at the upper-right corner of the graph because 100 percent of the population always owns 100 percent of the unit being measured. The inequality shown in the Lorenz curve reflects the difference between the line of equality and the measured distribution. These areas can be used to calculate the Gini where G = A / (A+B) (Figure 2).
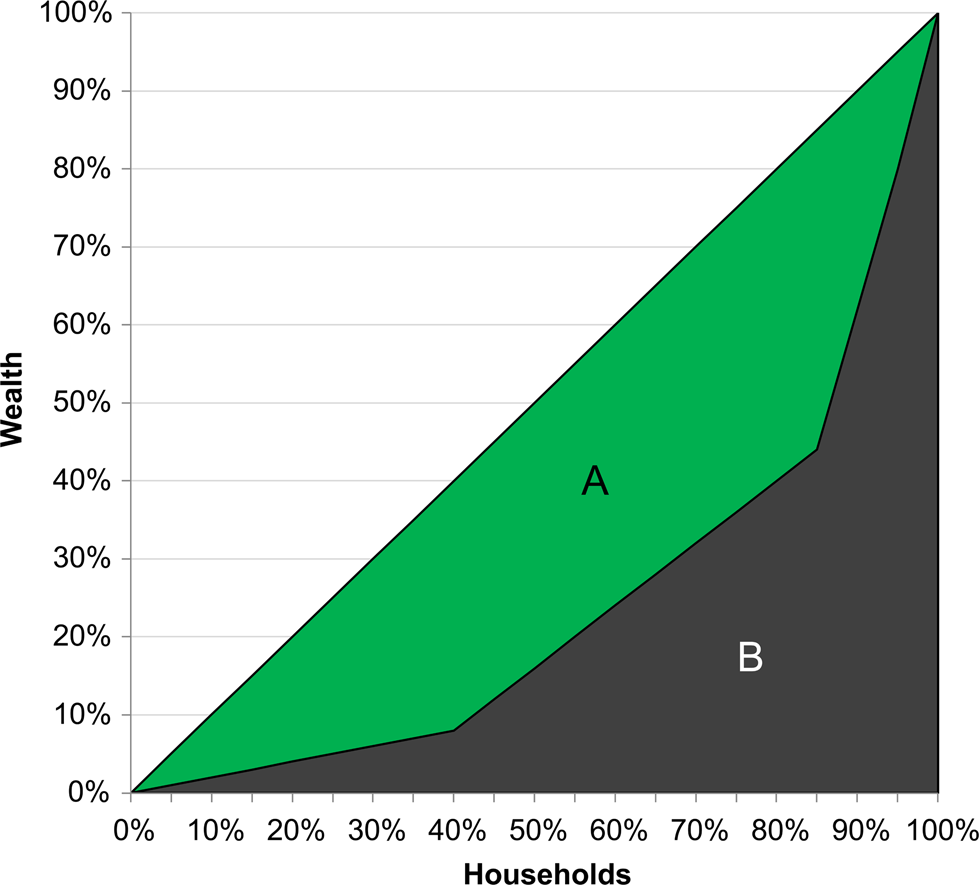
Figure 2. The Lorenz curve and its mathematical relationship to the Gini, where the Gini = AreaA / (AreaA + AreaB) reproduced from Chase (Reference Chase2017:Figure 4). The sharp curves of this Lorenz emerge because the underlying dataset consists of points with one of three different values. Created by the authors.
When comparing Gini, the Lorenz curves should also be considered (following Peterson and Drennan Reference Peterson, Drennan, Kohler and Smith2018:39–40). Two distributions with similar sample sizes that have the same Gini may have vastly different Lorenz curves (see Sitthiyot and Holasut Reference Sitthiyot and Holasut2020:7). Although Uxbenká and Cuexcomate (Figure 3) have similar Gini, in this case approximately 0.49, that value obscures contrasting distributions. At Cuexcomate, one larger household compared to the rest of the houses results in the quick upturn of the Lorenz curve, creating a “hockey stick” appearance. At Uxbenká, there are a few larger households of varying size, resulting in a more gradual Lorenz curve. Thus, interpretation of Gini alone does not showcase the concentrated nature of wealth at Postclassic Cuexcomate in central Mexico (Smith et al. Reference Smith, Dennehy, Kamp-Whittaker, Colon and Harkness2014), in contrast to Classic Maya Uxbenká in southern Belize (Thompson et al. Reference Thompson, Feinman and Prufer2021a), despite similar Gini values.

Figure 3. Both (a) Cuexcomate (Smith et al. Reference Smith, Dennehy, Kamp-Whittaker, Colon and Harkness2014) and (b) Uxbenká District 2 (D2) (Thompson et al. Reference Thompson, Feinman and Prufer2021a) exhibit nearly identical Gini, 0.49, with similar sample sizes, but the two Lorenz curves show vastly different distributions of wealth based on house size. Cuexcomate has a single large residence driving its high inequality (and the steep final part of its curve), while Uxbenká has multiple larger residences. Created by the authors.
Visually, measuring the Gini from the Lorenz curve requires calculus, but we can use Reimann sums—approximation of a curve's area with rectangles (Stewart Reference Stewart2005:343–350). The Excel file available in conjunction with this article does exactly this (see supplementary materials) and facilitates the calculation of both the Gini and the Lorenz curve developed from Shryock (Reference Shryock1976:98–99). In the file, basic descriptive statistics are calculated on the dataset and four graphs are produced to visualize the univariate data. As an added benefit, the nature of a spreadsheet permits users to investigate individual cells and see the calculations. Importantly, this Excel file makes the algorithms accessible to anyone who is curious, especially to those without programming experience.
Although the default Gini provides a measure of inequality, it requires correction for smaller sample sizes, generally less than 50. As such, we report the “corrected” Gini throughout this Compact Special Section. Since the Gini is an approximation of the area under the Lorenz curve, small samples will naturally have a lower Gini than larger ones because of the area of the far-right rectangle. A triangular area is always included under both curves that alters the results for smaller datasets (Figure 4). Other methods exist to correct for small sample sizes, through bootstrapping (Dixon et al. Reference Dixon, Weiner, Mitchell-Olds and Woodley1987) or new inequality equations (Bowles and Carlin Reference Bowles and Carlin2020), but the simple correction provided by Deltas (Reference Deltas2003) has an additional advantage in that it can be calculated for existing Gini datasets as long as the sample size has been reported. To calculate this for existing data, use the following formula: CorrectedGini = Gini * (SampleSize / (SampleSize − 1)). In addition, for larger sample sizes (generally over 50) this correction has a negligible effect (since 51/50 is just 1.02, a 2 percent increase), and the Gini and corrected Gini provide the same value to two decimal places (see Deltas Reference Deltas2003: Table 1).
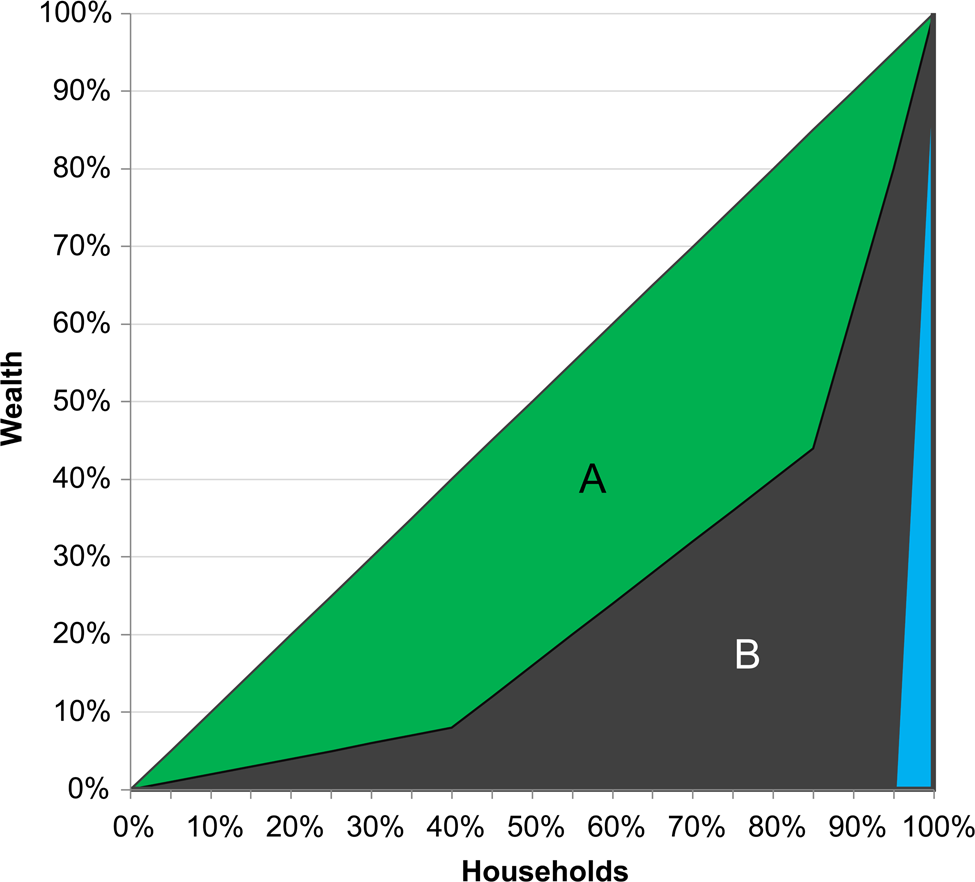
Figure 4. Updating Figure 2 to show the “corrected” Gini, the area of B is modified to remove the bottom-right triangle shown Figure 2 (since the sample size here is 20, 1/20 or 5 percent, is the edge length of that triangle). This area is always included in the default Gini calculation with Reimann sums, but needs to be accounted for in smaller samples (see Deltas Reference Deltas2003). In large samples, the area under the bottom-right triangle becomes negligible. Created by the authors.
Table 1. Area and volume Gini and additional information for Caracol, Belize. The sample sizes differ because two residences are too close to the edge of the LiDAR-derived DEM to generate accurate volumes.

Other essential parts of reporting a Gini require code to calculate, which we provide (see supplementary materials). The R script used in all case studies throughout this Compact Special Section provides additional visualizations of the univariate data distributions with box-n-whisker plots (see Shennan Reference Shennan1997:45–46), as well as calculations for the 95 percent confidence intervals (CIs) for the Gini data using bootstrapping methods (Dixon et al. Reference Dixon, Weiner, Mitchell-Olds and Woodley1987; Peterson and Drennan Reference Peterson, Drennan, Kohler and Smith2018:53) to resample the data up to 1,000 times. These CIs show how accurate the central Gini measurement is by repeatedly resampling the data (bootstrapping) and provide an indicator of robustness. The larger the sample size and the less variation between items being measured, the closer the CIs will be to the reported Gini. For example, large datasets in this Compact Special Section such as Caracol (described further below) and the Rosario Valley centers (Shaw-Müller and Walden Reference Shaw-Müller and Walden2023) have negligible Cis, while smaller datasets, such as Kaq'ru' Ha' from southern Belize, has a larger CI (Thompson et al. Reference Thompson, Chase and Feinman2023).
When comparing Gini coefficients between two centers, these CIs should be included in our interpretations (Figure 5). If both centers have CIs with no overlap, then they represent distinct distributions. If either end of the CIs overlap without extending over the central value, then the distributions are quite likely different. Finally, if the CIs overlap the central Gini, then the two values come from very similar distributions and should be treated as essentially equivalent. In any of these cases, the basic metrics on distributions provide additional and helpful information for disentangling the nature of overlapping relationships. For example, the percentile distributions may be similar, but the ranges and means may be completely different (Walden et al. Reference Walden, Hoggarth, Ebert, Shaw-Müller, Weiyu, Yijia, Ellis, Meyer, Biggie, Watkins, Guerra and Awe2023).

Figure 5. When comparing Gini data, the confidence intervals provide information on how similar or different the potential distributions are, with greater overlaps between confidence intervals and central Gini suggesting more similarities in the underlying datasets. Created by the authors.
Gini coefficients and Lorenz curves provide easy yet powerful ways to visualize and consider inequality in conjunction with other methods of contrasting two or more distributions; however, both metrics provide only one perspective based on a singular dataset. They show percentile differences in a population, and provide simplified, composite measures of unevenness in a distribution for a single variable. In general, multiproxy approaches may illuminate other variations that existed in past societies, especially those that will be obscured by using a single metric.
Regardless, any metric used in direct comparisons of Gini must be of the same basic type of data—house size, amount of polychrome pottery, and so on. They should also be of the same unit of measure. For example, Gini of house size area and volume should not be directly compared (see Thompson et al. Reference Thompson, Chase and Feinman2023). The percentile nature of both metrics also means that they favor larger sample sizes and tend to have larger error ranges with smaller datasets. In turn, subsets of data—such as districts or neighborhoods within a city—should not be expected to replicate larger patterns in a fractal nature (e.g., Thompson et al. Reference Thompson, Feinman and Prufer2021a). Despite these caveats, so long as researchers consider the potential fragilities of these metrics and other information and statistics about the distributions, Gini coefficients and Lorenz curves provide powerful tools for comparing wealth distributions.
Three comparative models
Multiple approaches, datasets, and research projects have analyzed inequality in historic and prehistoric societies, but thus far, only a few models exist that provide broad comparisons. These examples provide important grounding points for considering inequality. Each of these studies provides synthetic analysis, but also contains some shortcomings, leaving room for continued improvement in subsequent research.
Borgerhoff Mulder and colleagues (Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009) provide a perspective on changes in relative inequality over time between material, relational, and embodied wealth among small-scale societies (Figure 6). They highlight general trends, focusing on the increasing importance of material wealth and the declining importance of relational wealth and embodied wealth, as the degree of sedentism in a society increases. However, their datasets are not directly comparable with those of residential size used here, and wide variance exists within each of the wealth datasets analyzed. The fundamental perspective on change in relative importance and degree of inequalities over time provides a reasonable hypothesis to investigate with future research, and the diversity of data used in Borgerhoff Mulder and colleagues’ (Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009) study provides potential avenues for future research in other regions.

Figure 6. Expected differences in wealth metrics and aggregated Gini metrics for small-scale societies. From Borgerhoff Mulder et al. Reference Borgerhoff Mulder, Bowles, Hertz, Bell, Beise, Clark, Fazzio, Gurven, Hill, Hooper, Irons, Kaplan, Leonetti, Low, Marlowe, McElreath, Naidu, Nolin, Piraino, Quinlan, Schniter, Sear, Shenk, Smith, von Rueden and Wiessner2009:Table 2. Created by the authors.
Boix (Reference Boix2015) provides a game theory perspective on how metrics of income-based inequality should change based on governance (Figure 7). While these metrics may not be directly comparable with residential size-based Gini coefficients, they do provide a platform for contextualizing the impact of local administrative strategies on inequality. However, archaeological analyses (see Carballo Reference Carballo, Hirth, Carballo and Arroyo2020:78; Chase Reference Chase2021:260–267) using Boix (Reference Boix2015) have yet to show that the residential Gini represent income. Rather, they seem to reflect that more collective groups should exhibit lower Gini than more autocratic societies because more collective societies place greater checks and balances on the ability of any one individual or family to concentrate wealth (see also Thompson et al. Reference Thompson, Feinman and Prufer2021a). Boix's analysis (Reference Boix2015:64–65, 85–87) shows expected Gini ranging from 0.15 to 0.56, with 0.15 for true republics, 0.19 for imperial republics, and a theoretical value of 0.56 for monarchies with a practical limit of 0.44 for actual cases. The expected income flows between more collective and more autocratic governing systems range between 0.15 and 0.44 (Boix Reference Boix2015) and parallel the income values of 0.2 to 0.4 identified by Piketty (Reference Piketty2014:266–267).

Figure 7. Expected Gini coefficients based on the game theory model from Boix (Reference Boix2015:64–65, 85–87), focusing on higher inequalities in systems under a single ruler or ruling family (e.g., monarchy) versus those with competing power centers (e.g., republic and imperial republic). Created by the authors.
Finally, for the third model, Kohler et al. (Reference Kohler, Smith, Bogaard, Peterson, Betzenhauser, Feinman, Oka, Pailes, Prentiss, Stone, Dennehy, Ellyson, Kohler and Smith2018) provide a broad comparison of settlements based on residential sizes from a global sample. However, their residences include mixtures of the three house size definitions outlined above, which would alter these values. Additionally, the value for Teotihuacan uses the lower Gini of 0.12 (Smith et al. Reference Smith, Dennehy, Kamp-Whittaker, Colon and Harkness2014:Table 1), a value that is currently being updated to 0.41 (Michael E. Smith, personal communication 2021). The city of Caracol was also misplaced in the governance table and can be placed in the intermediate group of governance (see Feinman and Carballo Reference Feinman and Carballo2018). A modified version of Table 11.5 from Kohler et al. (Reference Kohler, Smith, Bogaard, Peterson, Betzenhauser, Feinman, Oka, Pailes, Prentiss, Stone, Dennehy, Ellyson, Kohler and Smith2018) accounts for these two changes (Figure 8). As a result, these data suggest that the initial hypothesis that more autocratic cities exhibit higher Gini holds (see also Feinman and Nicholas Reference Feinman, Nicholas, Bussman and Helms2020), but it also suggests that the intermediate and collective categories may be more complex. Hopefully, future analysis can more fully test these ideas (Kohler and Thompson Reference Kohler and Thompson2022).
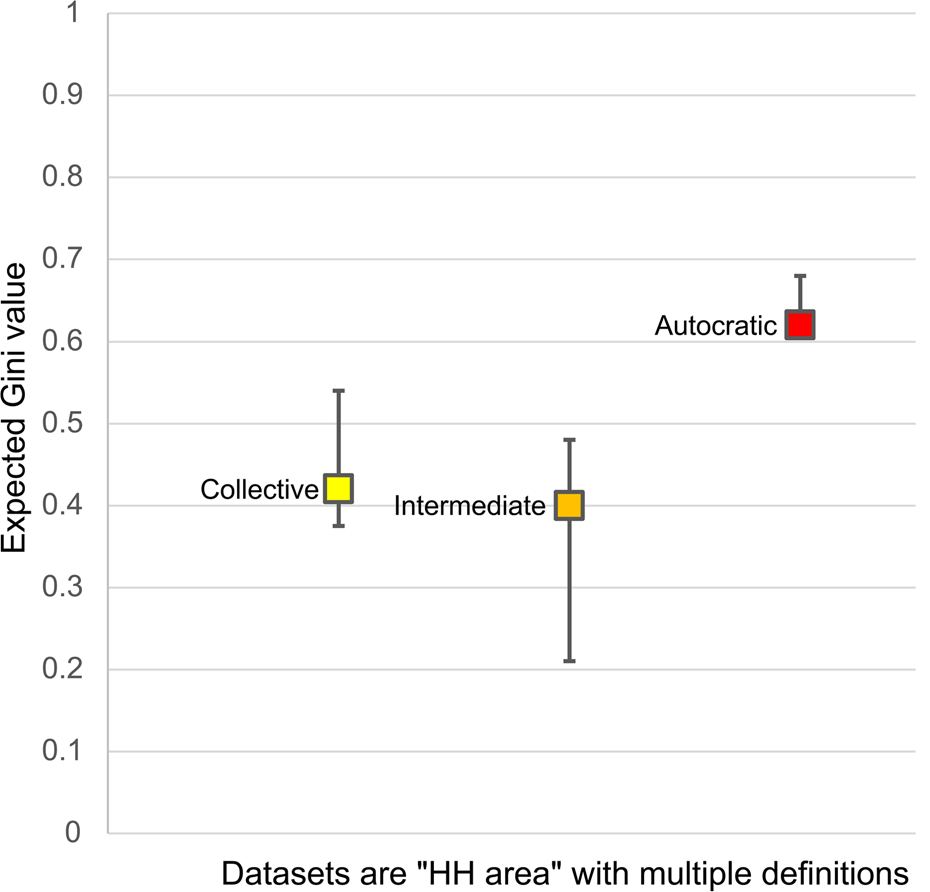
Figure 8. Inequality and governance based on residential size, which suggests higher degrees of inequality among autocratic cities and more muted inequality among both collective and, importantly, intermediate cities. Modified from Kohler and colleagues (Reference Kohler, Smith, Bogaard, Peterson, Betzenhauser, Feinman, Oka, Pailes, Prentiss, Stone, Dennehy, Ellyson, Kohler and Smith2018:Table 11.5). Created by the authors.
Archaeological analysis of inequality in Mesoamerica remains an active area of scholarly inquiry, and other analyses of governance have yielded preliminary results showing that more collective forms of governance were more prevalent than initially expected (Carballo et al. Reference Carballo, Feinman and Corral2022; Chase Reference Chase2021; Feinman and Carballo Reference Feinman and Carballo2018, Reference Feinman and Carballo2022; Thompson and Prufer Reference Thompson and Prufer2021), although additional research is still needed. The complexity of measuring income versus capital (Piketty Reference Piketty2014:50–52, 266–267) creates additional challenges for directly applying the game theory models from Boix (Reference Boix2015). Additionally, while this Compact Special Section focuses on area and volume of residences, volume measures must consider the accretion of architecture over generations (Hutson Reference Hutson2016:151–152, Reference Hutson, Hutson and Ardren2020:411–412) in long-lived centers versus short-lived centers in our interpretations of inequality. As such, to reflect on governance, residential-based inequality measures must account for both the longevity of occupation and potential oscillations between more collective and more autocratic forms of governance over time at those centers. Nevertheless, the accretion of house mounds, like the accumulation of domestic wealth, is generally a multigenerational endeavor. However, future work is required to fully disentangle the complex—and essential—societal interactions of governance and inequality, and to delve into diachronic analyses of inequality.
Measuring house size as wealth
This Compact Special Section presents six measures of residential-level, house-size inequality in an effort to standardize prior research on ancient Maya centers. These six arise from the analytical parameters of either area (m2) or volume (m3) and residential units of analysis, including the entire plazuela, all structures in a plazuela, or individual house mounds (Figure 9; see also Thompson et al. Reference Thompson, Feinman and Prufer2021a:Figure 3, Reference Thompson, Chase and Feinman2023). These measures provide differing data and resulting Gini metrics, thus influencing interpretations of inequality. We note that not all metrics are equally calculable for all research areas, depending on local taphonomic conditions (e.g., modern agricultural activities; see Munson et al. Reference Munson, Scholnick, Ramón and Aragon2023; Walden et al. Reference Walden, Hoggarth, Ebert, Shaw-Müller, Weiyu, Yijia, Ellis, Meyer, Biggie, Watkins, Guerra and Awe2023), the form of residential settlement (e.g., Marken Reference Marken2023), and legacy survey mapping (e.g., Richards-Rissetto Reference Richards-Rissetto2023).

Figure 9. Residential units of analysis: (1) individual house mounds shown in different shades of green; (2) all structures per plazuela as the summed part of all the green colored structures; and (3) entire plazuela group as all the green and all the yellow parts of this image. Created by the authors.
There are several methods to calculate the analytical parameters of area and volume of house size. Area can be calculated directly in a GIS program, using the residential feature class shapefile or the summation of area covered by raster cells under a residence. Area is easy to calculate from prior archaeological maps and other datasets, which has led to widespread use of area-based house size Gini datasets (e.g., Kohler and Smith Reference Kohler and Smith2018). Because of this, house size area is frequently used in cross-cultural and cross-temporal comparisons. Nonetheless, these measures require additional investigation to understand the potential discrepancies and nuances between the often smaller residences associated with nuclear families and the often larger residences associated with extended family groups, as well as the effects of multigenerational occupation on inequality metrics.
Residential volumes, in contrast, are more difficult to calculate. As part of this Compact Special Section, the lead author created a Python script for calculating volume (available in the supplementary data) to standardize this approach, with authors using ArcMap 10.8.1, 10.8.2, or ArcPro 2.9 on Windows 10 or 11 for analysis. At least four prior analyses of volume, each with its own method, have been used in the Maya area (Chase Reference Chase2017:34; Ebert et al. Reference Ebert, Hoggarth and Awe2016:289; Šprajc et al. Reference Šprajc, Marsetič, Štajdohar, Góngora, Ball, Olguín and Kokalj2022:7; Stanton et al. Reference Stanton, Ardren, Barth, Fernandez-Diaz, Rohrer, Meyer, Miller, Magnoni and Pérez2020:6–7). The new method provided here combines aspects of these approaches to measure volume on uneven surfaces. From an algorithmic perspective, this method takes both a polygon shapefile and a digital elevation model (DEM) raster as inputs. From these, the algorithm calculates volume using a natural neighbor interpolation (see Sibson Reference Sibson and Barnett1981), using elevation values under the nodes (vertices) of the shapefile to construct a non-flat surface under the input polygons based on local topography. This allows digitized structures to exclude the volume of the platform beneath them, but may also include hilltop volume when platforms are measured (see Horn III et al. Reference Horn, Tran and Ford2023). The difference between the raster cells in this newly interpolated surface and the DEM below each shapefile are then summed to provide volume per unique feature ID in a separate Excel file.
Both area and volume were applied to the three residential units of analysis to standardize measures of house size for calculating Gini in this Compact Special Section. Each of the three units of analysis provides different perspectives on residential dynamics and the use of space. However, not all archaeologists can map or identify all three units of analysis, due to variations in pedestrian and remotely sensed survey data, local architectural styles and materials, ancient land practices, and the heterogeneity of ancient Maya settlement systems (see Thompson et al. Reference Thompson, Walden, Chase, Hutson, Marken, Cap, Fries, Piedrasanta, Hare, Horn, Micheletti, Montgomery, Munson, Richards-Rissetto, Shaw-Müller, Ardren, Awe, Kathryn Brown, Callaghan, Ebert, Ford, Guerra, Hoggarth, Kovacevich, Morris, Moyes, Powis, Yaeger, Houk, Prufer, Chase and Chase2022:10–13).
Case study from Caracol, Belize
For Caracol—a Classic Maya city that spans over 200 km2 in modern Belize, with a population of over 100,000 during its apogee (see also Chase and Chase Reference Chase and Chase2017; Chase et al. Reference Chase, Chase, Morris, Awe and Chase2020)—the entire plazuela provides the ideal residential form for measurement (Figure 10). This is due to both the nature of the LiDAR dataset and the way that the residents of Caracol built and used their houses. Within the LiDAR data for this city (Chase et al. Reference Chase, Chase, Weishampel, Drake, Shrestha, Clint Slatton, Awe and Carter2011, Reference Chase, Chase, Awe, Weishampel, Iannone, Moyes, Yaeger, Kathryn Brown, Shrestha and Carter2014), under 50 percent of individual structures can be accurately recognized, while the recovery rate of plazuela groups is higher, between 60 and 80 percent (see Arlen F. Chase et al. Reference Chase, Chase, Chase, Chase, Chase, Chase and Chasein press). Similar trends have been noted in other Maya LiDAR datasets (Garrison et al. Reference Garrison, Thompson, Krause, Eshleman, Fernandez-Diaz, Dennis Baldwin and Cambranes2022; Thompson Reference Thompson2020; Yaeger et al. Reference Yaeger, Kathryn Brown and Cap2016). Furthermore, excavations at Caracol identified multiple functions for the structures within a plazuela, including ritual buildings, kitchens, and sweat baths, in addition to sleeping areas (Chase and Chase Reference Chase and Chase2014). This suggests occupation by extended family groups (see Adrian S.Z. Chase et al. Reference Chase, Chase, Chase, Chase, Chase, Chase and Chasein press), and that structure-based estimates would not yield data related to residential-level inequality and, at least in this context, would divide the actual residential units into smaller spaces unlinked to individual families.

Figure 10. The Dos Aguadas residential group (in Caracol), shown with multiple visualizations, including: (a) sky-view factor (Zakšek et al. Reference Zakšek, Oštir and Kokalj2011); (b) local relief model (Chase Reference Chase2016:890–891); and (c) its illustrated survey map rendition. Reproduced with permission from Chase and Chase Reference Chase and Chase2014:Figure 2. Created by the authors.
Residential volumes at Caracol also likely provide more of a perspective on long-term, multigenerational wealth accumulation. For example, at the time of writing in 2023, the oldest excavated residence had continuous occupation for over 1,500 years (Chase and Chase Reference Chase and Chase2006), suggesting that Caracol's volume metrics do not provide the most accurate assessment of wealth inequality for a single phase (following Hutson Reference Hutson2016:151–152, Reference Hutson, Hutson and Ardren2020:411–412; see also Shaw-Müller and Walden Reference Shaw-Müller and Walden2023). The differences between actual and measured residential volume are also compounded both by substantial subsurface modifications down to bedrock (Chase and Weishampel Reference Chase and Weishampel2016:360) and by a shift from denser but more labor-intensive construction in the Early Classic towards one that was more labor-efficient per cubic meter in the Late Classic. Energetic analyses (Abrams Reference Abrams1994; Erasmus Reference Erasmus1965) amortized over time would provide a more accurate version of volume-based wealth inequality; however, this endeavor would require decades of additional excavation to reach a reasonable household sample, given the population size and spatial scale of Caracol. Additionally, the provision of a comparative metric—along with its caveats—remains preferable for collaborative research. As with all aspects of archaeology, multiple lines of evidence provide a stronger foundation for research results than a single metric, and we should always test and retest what we think we know given an ever-expanding empirical record. Future research will incorporate additional residential information and indices to help establish how well area and volume match with or diverge from other forms of material, embodied, and relational inequality (in the interim, see Chase Reference Chase2021:197–267 and Munson et al. Reference Munson, Scholnick, Ramón and Aragon2023 for additional discussion).
Area and volume Ginis had previously been calculated at Caracol based on a sample of 4,058 plazuela groups and yielded Gini coefficients and Lorenz curves of 0.34 for plazuela area and 0.60 for plazuela volume (Chase Reference Chase2017). The results of this re-analysis, shown in Figure 11 and Table 1, reveal that despite nearly doubling the sample size to more than 7,700 (Chase Reference Chase2021), the results do not change (see those initially reported in Chase Reference Chase2017:Figure 3). The Gini remain consistent, around 0.34 for area and 0.60 for volume—and future research can address intra-site patterns (similar to Marken Reference Marken2023). However, the initial 2017 analysis included neither confidence intervals nor the additional distributional data (see Table 1), which provide additional data for inter-site comparisons.

Figure 11. Area (m2) and volume (m3) Lorenz curves for Caracol's plazuela groups. Please note that larger sample sizes can—but do not necessarily—lead to smoother curves. Created by the authors.
Compact Special Section: Maya inequality summaries
This Compact Special Section includes a wide breadth of data from nearly two dozen ancient Maya centers. In aggregate, these data provide insights into the diversity and heterogeneity in settlement composition and inequality present among these centers. The short-article format of this Compact Special Section also allowed authors to focus on unique aspects of wealth and inequality relevant to their own research, thereby providing multiple perspectives and interpretations on this topic.
Thompson and co-authors (Reference Thompson, Chase and Feinman2023) build on their previous work in southern Belize (Thompson and Prufer Reference Thompson and Prufer2021; Thompson et al. Reference Thompson, Feinman and Prufer2021a, Reference Thompson, Feinman, Lemly and Prufer2021b), outlining issues of household definitions (residential units of analysis) and the distinctions between area and volume metrics (analytical parameters). Their analyses demonstrate the diversity present in these metrics and help to illustrate why “like” should be compared to “like”—that is, Gini for plazuelas should be compared with Gini for plazuelas, rather than with all structures per plazuela or individual house mounds. They also provide insights into how to use all six metrics—three units of analysis (i.e., residential definitions] and two units of measurement (i.e., area versus volume)—and about how this yields more insights into inequality in southern Belize than a single metric on its own.
Hutson and colleagues (Reference Hutson, Stanton and Ardren2023) analyze Coba in relation to previously presented Gini at other centers in the northern lowlands—Chunchucmil, Dzibilchaltun, Sayil, and Komchen (see also Hutson Reference Hutson, Hutson and Ardren2020). Their analyses showcase some of the issues associated with relating governance type directly to the Gini without considering other relevant datasets, as discussed above. The authors also suggest that prior assumptions of declining inequality over time in the Northern Lowlands need to be reassessed with new data and analyses. Their diachronic focus on change in inequality and standards of living over time has direct modern relevance.
Shaw-Müller and Walden (Reference Shaw-Müller and Walden2023) assess legacy data from the Rosario Valley. Their research focuses on the implications of inequality and residential form in an area occupied by multiple ethnic and linguistic communities—both Maya and non-Maya—in the past. Initial occupation by non-Maya peoples was followed by in-migration of Maya peoples. This process may have resulted in some of the residential inequality observed in the Rosario Valley. The authors also explore the idea of residential life cycles, immigration, and how both concepts articulate with inequality.
Marken (Reference Marken2023) focuses on El Peru-Waka', the densest Classic period Maya city (Marken et al. Reference Marken, Ricker, Rivas and Maxson2019), and explores intra-site variations in density and residential form between the urban core and hinterland as it articulates with inequality based on house size. Using the subdivisions of urban, periurban, and rural showcases the effect of aggregated inequality as a result of the greater build-up of volume and residential area in the urban core. When analyzed separately, similar patterns of inequality exist within each part of the center, which differs from the aggregated pattern of inequality.
Horn III and co-authors (Reference Horn, Tran and Ford2023) examine El Pilar and the dichotomy of rulers and subjects, as well as issues in household form, focusing on primary and secondary residential units. Their research also focuses on residential functions and labor investments, highlighting the fact that wealthier residences in this region of western Belize were using hilltops and the natural topography to inflate the perceivable architectural volume of their residences. Their discussions illuminate how perceptions of inequality relate to both modern definitions used by archaeologists and the ancient practices of a settlement's inhabitants.
Canuto and colleagues (Reference Canuto, Auld-Thomas, Yagi and Barrientos Q.2023) focus on the centers of La Corona and Achiotal, while investigating inequality at a larger, regional scale. Their research further addresses the issues of how to incorporate single mounds, and the difficulties in identifying these features using remotely sensed LiDAR data. Their analyses provide insights into cluster methods, inequality, and broader questions about residential form.
Walden and co-authors (Reference Walden, Hoggarth, Ebert, Shaw-Müller, Weiyu, Yijia, Ellis, Meyer, Biggie, Watkins, Guerra and Awe2023) employ the Gini to examine differential patterns of labor control at the polities of Baking Pot and Lower Dover in the Belize River Valley. While the polity of Baking Pot emerged in the Preclassic and grew gradually, the polity of Lower Dover arose in the Late Classic and supplanted three long-established local elite regimes. They draw on prior work and measures of labor control at the two polities to show that political control of labor was far more centralized at Baking Pot, compared to Lower Dover, where intermediate elites still commanded a significant proportion of commoner labor, despite the rise of the polity (Walden et al. Reference Walden, Ebert, Hoggarth, Montgomery and Awe2019).
Montgomery and Moyes (Reference Montgomery and Moyes2023) assess Las Cuevas and its surrounding area in the Vaca Plateau of Belize. Their research provides multiple Gini for the region, each center, and populations proximate to ritually imbued caves. They focus on multiple settlement areas at different scales, along with careful discussion of potential issues with Gini analyses.
Richards-Rissetto (Reference Richards-Rissetto2023) focuses on Copan in western Honduras. Her research includes the standard metrics advanced in this Compact Special Section, but also includes an additional discussion of three-dimensional architectural models as an inequality measure. This measure could potentially be used among others with high-resolution LiDAR data, and expends prior uses of computational modelling to reconstruct past life in Copan (Richards-Rissetto Reference Richards-Rissetto, White and Surface-Evans2012, Reference Richards-Rissetto2017).
Munson and co-authors (Reference Munson, Scholnick, Ramón and Aragon2023) discuss settlement in the Upper Usumacinta Confluence Zone of Guatemala. The authors close out this Compact Special Section by presenting other measures of inequality and advocating for the use of multiple metrics beyond house size (see also Munson and Scholnick Reference Munson and Scholnick2022). In particular, this research investigates house height and non-residential aspects related to the quality of life. Although residential size provides one metric, investigations of inequality with multiple parameters provide additional insights and illuminate the nuances archaeologists must consider when attempting to understand wealth, disparity, and inequality in the past.
Wealth inequality results
Taken together, the initial results of these analyses provide new perspectives on ancient inequality in the Maya region. With these data, we investigate the relationships between sample size (as a proxy for population), range in residential sizes, and median residential size using plazuela areas and volumes—the residential form measured by most authors. Although the results are not perfect regressions, they do reveal preliminary patterns of residential inequality among these centers. We find that (1) the most populous centers (those with the largest sample sizes) have reduced inequality with sample size; (2) variations in the ranges of house sizes do not provide a clear relationship with inequality; and (3) median residential size is weakly and inversely correlated with inequality. Finally, the distributions of these Gini coefficients suggests that plazuela area measures may align with total inequality (e.g., income and capital) and volume measures with capital inequality, with neither matching the expectations for labor inequality (Piketty Reference Piketty2014:266–267), albeit this concept requires additional research.
First, we expected that larger populations, assumed by larger sample sizes, would lead to higher inequality, under the assumption that more residences co-located in a single settlement would enable the wealthiest families to access and harness more labor or the results of that labor. The data mostly agree with this hypothesis, except for the two largest cities in this sample (Figure 12). Caracol and Coba were among the most populous Classic Maya cities (Adrian S.Z. Chase et al. Reference Chase, Chase, Chase, Chase, Chase, Chase and Chasein press; Stanton et al. Reference Stanton, Hutson, Ardren, Chase, Chase and Chasein press), but these higher populations did not necessarily translate into greater residential inequality, with plazuela area Ginis ranging from (roughly) ~0.34 to 0.40, similar to the other Maya cities in the sample (Figure 12). This finding contradicts established economic expectations that the largest cities always have the highest Ginis (Behrens and Robert-Nicoud Reference Behrens and Robert-Nicoud2014).

Figure 12. Plazuela area (m2) Gini plotted against the sample size (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. Both Caracol and Coba diverge from the correlation between increasing sample size (as a proxy for population) and increasing inequality. This suggests that both Coba and Caracol may have engaged in inequality reduction strategies. LCMT = Las Cuevas-Monkey Tail; UUCZ = Upper Usumacinta Confluence Zone. Created by the authors.
Additionally, these two cities deviate from the trend present among the other cities in our Compact Special Section, where increasing sample size (proxy for population) is tied to increasing Gini. Research at Caracol has highlighted its symbolic egalitarianism and inequality reduction during a 100-year period of the Late Classic (Chase and Chase Reference Chase and Chase2004, Reference Chase and Chase2009, Reference Chase and Chase2017:213–216), which this analysis seems to corroborate. Although this pattern is clearer for area measurements (Figure 12) than for volume (Figure 13), this is partly because fewer centers have volume data for the entire plazuela. Additionally, centers with smaller sample sizes, such as some in southern Belize, have larger error ranges (Figure 12). Likewise, the confidence intervals reveal how much a single large household, in combination with a smaller sample size (around 100, rather than thousands), can impact Gini error ranges (Ix Kuku'il; Figure 13).

Figure 13. Plazuela volume (m3) Gini plotted against the sample size (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. The trend of increasing sample size and higher inequities appears to hold, except for the two largest centers of Coba and Caracol. LCMT = Las Cuevas-Monkey Tail; UUCZ = Upper Usumacinta Confluence Zone. Created by the authors.
Although the actual relationship between population and inequality requires future analysis with additional cities, these incipient results suggest that social processes, mechanisms, or activities leading to inequality in residential size played out differently at these centers. Among many, increases in population largely parallel increases in inequality, but, counterintuitively, at the largest centers inequality is much lower than expected. This result deviates from modern expectations and suggests that there were social mechanisms at both Coba and Caracol that acted to reduce inequality; on the other hand, for the smaller cities in this sample, with populations in the thousands to ten thousand, this trend holds. Some centers, like Copan, La Corona, and El Pilar, may have served as essential “gateways” (or “brokers,” as per Peeples and Haas Reference Peeples and Haas2013) in exchange networks (see Halperin Reference Halperin2014; Thompson et al. Reference Thompson, Feinman, Lemly and Prufer2021b; and Tokovinine Reference Tokovinine2013). However, a better understanding of regional trade networks is required to understand the roles that centers served in the multiple overland and riverine routes used in the Classic period (see, e.g., Chase and Chase Reference Chase and Chase2012 on Belize Red; Feinman et al. Reference Feinman, Nicholas, Golitko, Feinman and Riebe2022 on obsidian; or McKillop Reference McKillop2019 on salt).
Second, we expected that larger ranges in residential size would lead to higher Gini coefficients. In other words, the wider the gulf between the largest and smallest residences (e.g., the richest and poorest), the higher we expect the Gini to be. However, these data do not clearly support this hypothesis for either area (Figure 14) or volume (Figure 15). Instead, these data indicate that the absolute difference between the largest and smallest residences provide a poor overall indicator of the resulting Gini over the relative sizes of the intermediate residences. In other words, the variation in Gini is not a direct function of outliers, the richest and poorest residences.

Figure 14. Plazuela area (m2) Gini plotted against the range between the smallest and largest residences (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. The expectation for larger ranges to be indicative of larger Gini does not hold. LCMT = Las Cuevas-Monkey Tail; UUCZ = Upper Usumacinta Confluence Zone. Created by the authors.

Figure 15. Plazuela volume (m3) Gini plotted against the range between the smallest and largest residences (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. The expectation for larger ranges to be indicative of larger Gini does not hold. LCMT = Las Cuevas-Monkey Tail; UUCZ = Upper Usumacinta Confluence Zone. Created by the authors.
Third, our expectation was that sets of data with higher median house size values would result in lower Gini. In other words, if the average house is larger—and there are more “people in the middle,” as shown by the higher median—then we expect to observe lower inequality. This view conforms with modern political and economic ideals for greater middle status representation in society. For plazuela areas (Figure 16), the general trend holds that centers with a higher median house size have a lower Gini. However, for plazuela volumes (Figure 17), these results are more inconclusive. So, higher median house size has some effect on reducing inequality, but does not preclude the concentration of wealth—in this case, plazuela volume—at the very top of society and the wealthiest elites.

Figure 16. Plazuela area (m2) Gini plotted against the median residential size (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. There is a weak pattern for increasing average residential size and lower inequalities. LCMT = Las Cuevas-Monkey Tail. Created by the authors.

Figure 17. Plazuela volume (m3) Gini plotted against the median residential size (at log-scale to facilitate comparisons) for datasets in this Compact Special Section. Unlike area (see Figure 16), the pattern among volume has more outliers. This suggests that while increasing medians may indicate more people in the middle, the effect does not make up for the potential concentration of wealth among the wealthiest households. LCMT = Las Cuevas-Monkey Tail; UUCZ = Upper Usumacinta Confluence Zone. Created by the authors.
Taken together, these results provide a microcosm of the challenges faced when employing a single metric to measure and interpret inequality. Instead, they provide a fertile basis to call for additional analyses that examine past qualities of life (Munson and Scholnick Reference Munson and Scholnick2022) or for integrating multi-parameter suites of data relevant to inequality (Blesch et al. Reference Blesch, Hauser and Jachimowicz2022). Yet the results do suggest a few trends. First, aside from unexpected inequality mitigation in the two largest centers, increasing population may be a factor in increasing inequality for smaller centers, although larger samples are needed. Second, the range in house size between the largest and smallest residences—that is, the extreme richest and poorest—provides a weak indicator of overall inequality. Finally, higher median house size (more people in the middle) is slightly linked to lower inequality, even if the effect can be hidden by variation among the largest residences. Each of these will require future analyses and additional data to investigate, along with other comparisons among these distributions.
That said, one other important pattern emerges. The lowest Gini for plazuela area in these datasets are around 0.3, while the highest are closer to 0.7, and the lowest Gini for plazuela volume in these datasets are around 0.5 while the highest are closer to 0.85. These values differ slightly from those generally expected for distributions of labor income (0.2–0.4), capital ownership (0.6–0.9), and total inequality (0.3–0.5), as discussed by Piketty (Reference Piketty2014:266–267), but provide an avenue for future investigation. Additionally, the observed ranges for plazuela area and volume Gini fall outside of the theoretical modeling of income-based inequality (0.15–0.44) presented by Boix (Reference Boix2015). Taken together, neither plazuela area nor plazuela volume provides a reasonable proxy for income inequality, which makes intuitive sense, since we do not know the incomes of past peoples, and house size likely provides an indirect reflection of income. Instead, the values determined from plazuela areas are more aligned with expectations for total inequality (e.g., combined income and capital inequality) and plazuela volumes may be more related to capital inequality; however, this requires additional investigation.
Valediction
This research united a dozen archaeological projects from across the Maya Lowlands to facilitate and standardize inequality analyses of house sizes for Maya centers. Together, our efforts yielded incipient, yet promising results, showing that the relationships between sample size, range, and median residential sizes and inequality are not straightforward, but, rather, are complex and require detailed evaluations of descriptive statistics, Lorenz curves, and other information in conjunction with Gini coefficients to bolster our interpretations. We hope the Excel file, R code, and ArcGIS Python script (available in the supplementary materials) presented here will help to democratize research on ancient inequality, by facilitating the research of others who can now undertake these analyses using standardized approaches. Our aim is to foster the comparison of the same units of analysis, using the same analytical parameters and calculations, and to encourage their use on multiple lines of evidence and datasets, rather than a single metric and data type. At the same time, this research and many of the articles in this Compact Special Section highlight key considerations for comparative research. Combined Gini coefficients and Lorenz curves provide powerful tools for looking at and comparing the variation within distributions; however, it remains the task of the researcher to illustrate why and how that variation translates into inequality and how it impacted the lives of people in the past.
Supplementary materials
To view supplementary material for this article, please visit https://doi.org/10.1017/S095653612300024X.
Files, scripts, and code necessary to reproduce these analyses have been included in the supplementary materials. These include a word document outlining analyses, an Excel document to calculate Ginis, R code to generate confidence intervals, and the python script and toolbox used to create volume data in ArcMap 10.8.1, 10.8.2, and ArcPro 2.9.
Acknowledgments
The authors would like to thank all of the scholars who joined us for this Compact Section, our SAA symposium, and the Field Museum workshop on inequality. We would also like to thank the Institute of Archaeology in Belize, Instituto Nacional de Antropología e Historia de México, Instituto Nacional de Antropología e Historia de Guatemala, and Instituto Hondureño de Antropología e Historia for managing archaeological research in each country. Finally, the authors would like to thank three anonymous reviewers for improving the quality of this article.
Data availability statement
Following guidelines from the Institute of Archaeology for the country of Belize, full LiDAR data are not generally available, to help protect the country's archaeological heritage from additional looting.
Competing interests declaration
The authors have no competing or conflicts of interest, and all authors have contributed to this manuscript.
Funding statement
This research has benefited from past funding for LiDAR acquisition and analysis at Caracol, Belize, including the National Science Foundation (NSF#1822230), the NASA Space Archaeology Program (NNX08AM11G), and the Alphawood Foundation.





















