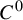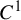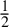1 Introduction and main results
1.1 Main results
This paper deals with foliations by curves in a two-dimensional symplectic setting. The questions we raise for such a foliation are as follows.
-
• When is it (locally or globally) symplectically homeomorphic to the straight foliation? (This will be defined precisely later.)
-
• What can be said on the foliation when it is invariant by a symplectic twist? (In this paper, we will say that a foliation is invariant by f if every leaf is (globally) invariant.)
-
• What can be said on a symplectic dynamics that preserves such a foliation?
Before going into detail, let us explain our motivations.
The first problem in which we were interested is the possible extension of the Arnol’d–Liouville theorem (see, for example, [Reference Duistermaat6]). This classical theorem concerns Hamiltonian dynamics associated to a
![]() $C^2$
Hamiltonian function endowed with a complete system of independent commuting
$C^2$
Hamiltonian function endowed with a complete system of independent commuting
![]() $C^2$
integrals. Then there exists an invariant
$C^2$
integrals. Then there exists an invariant
![]() $C^2$
foliation by Lagrangian submanifolds, and in the neighbourhood of every compact leaf of this foliation there exist symplectic
$C^2$
foliation by Lagrangian submanifolds, and in the neighbourhood of every compact leaf of this foliation there exist symplectic
![]() $C^1$
angle-action coordinates
$C^1$
angle-action coordinates
![]() $H: (q, p)\in {\mathcal U}\subset M\mapsto (\theta , I)\in U\subset \mathbb {T}^n\times \mathbb {R}^n$
such that at these coordinates:
$H: (q, p)\in {\mathcal U}\subset M\mapsto (\theta , I)\in U\subset \mathbb {T}^n\times \mathbb {R}^n$
such that at these coordinates:
-
• the invariant foliation is the straight foliation
 $I=\text {constant}$
;
$I=\text {constant}$
; -
• the flow is
 $(\theta , I)\mapsto (\theta +t\triangledown h(I),I)$
where h is a
$(\theta , I)\mapsto (\theta +t\triangledown h(I),I)$
where h is a
 $C^2$
function.
$C^2$
function.
In fact, there are two steps in this result.
-
• The first step consists in symplectically straightening the foliation via the chart H. The diffeomorphism H is defined via its generating function
 $S(q, I)$
. We recall that A priori this generating function S is only
$S(q, I)$
. We recall that A priori this generating function S is only $$ \begin{align*}H(q, p)=(\theta, I)\Longleftrightarrow\ \theta=\frac{\partial S}{\partial I}(q, I)\quad\text{and}\quad p=\frac{\partial S}{\partial q}(q, I).\end{align*} $$
$$ \begin{align*}H(q, p)=(\theta, I)\Longleftrightarrow\ \theta=\frac{\partial S}{\partial I}(q, I)\quad\text{and}\quad p=\frac{\partial S}{\partial q}(q, I).\end{align*} $$
 $C^2$
as the foliation was and the diffeomorphism H is only
$C^2$
as the foliation was and the diffeomorphism H is only
 $C^1$
, but because the invariant foliation is
$C^1$
, but because the invariant foliation is
 $C^2$
, we can say a little more: when I is fixed,
$C^2$
, we can say a little more: when I is fixed,
 $\Phi =H^{-1}$
is
$\Phi =H^{-1}$
is
 $C^2$
in the
$C^2$
in the
 $\theta $
-variables.
$\theta $
-variables.
-
• Then the second step consists in noticing that a symplectic flow that preserves every leaf of the straight foliation has to be a flow of rotations on every leaf.
In [Reference Arnaud and Xue3], the hypothesis concerning the regularity of the invariant foliation was relaxed and the invariant foliation was just assumed to be
![]() $C^1$
. In this case, when the Hamiltonian satisfies the so-called A-non degeneracy condition (which contains the case of Tonelli Hamiltonians), the authors proved the existence of a symplectic homeomorphism H straightening the invariant Lagrangian foliation, such that
$C^1$
. In this case, when the Hamiltonian satisfies the so-called A-non degeneracy condition (which contains the case of Tonelli Hamiltonians), the authors proved the existence of a symplectic homeomorphism H straightening the invariant Lagrangian foliation, such that
![]() $H^{-1}$
is
$H^{-1}$
is
![]() $C^1$
in the
$C^1$
in the
![]() $\theta $
variable and such that the flow is written in the chart
$\theta $
variable and such that the flow is written in the chart
![]() $(\theta , I)\mapsto (\theta +t\triangledown h(I),I)$
where h is a
$(\theta , I)\mapsto (\theta +t\triangledown h(I),I)$
where h is a
![]() $C^1$
function.
$C^1$
function.
Here we raise the problem of invariant
![]() $C^0$
foliation by invariant
$C^0$
foliation by invariant
![]() $C^0$
-Lagrangian tori. In high dimension, the first problem is to define what is a
$C^0$
-Lagrangian tori. In high dimension, the first problem is to define what is a
![]() $C^0$
-foliation by Lagrangian tori. An interesting discussion on this topic is provided in the appendix to [Reference Arnaud and Xue3], but here we will consider the simplest case: in dimension 2, any foliation by curves can be seen as Lagrangian. Also we will assume that the foliations that we consider are not too complicated, because they are (at least locally in
$C^0$
-foliation by Lagrangian tori. An interesting discussion on this topic is provided in the appendix to [Reference Arnaud and Xue3], but here we will consider the simplest case: in dimension 2, any foliation by curves can be seen as Lagrangian. Also we will assume that the foliations that we consider are not too complicated, because they are (at least locally in
![]() $C^1$
charts) foliations by graphs.
$C^1$
charts) foliations by graphs.
The dynamics will be that of symplectic twist diffeomorphisms. Let us give the definition here; it will be detailed and explained later in the text.
Definition. A symplectic twist diffeomorphism
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is a
$f:\mathbb {A}\rightarrow \mathbb {A}$
is a
![]() $C^1$
diffeomorphism such that:
$C^1$
diffeomorphism such that:
-
• f is isotopic to the identity;
-
• f is symplectic, that is,
 $f^*\omega =\omega $
where
$f^*\omega =\omega $
where
 $\omega $
is the standard symplectic form on
$\omega $
is the standard symplectic form on
 $\mathbb {A}$
;
$\mathbb {A}$
; -
• f has the twist property, that is, if
 $F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f, for any
$F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f, for any
 $\tilde \theta \in \mathbb {R}$
, the map
$\tilde \theta \in \mathbb {R}$
, the map
 $r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing
$r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing
 $C^1$
diffeomorphism from
$C^1$
diffeomorphism from
 $\mathbb {R}$
onto
$\mathbb {R}$
onto
 $\mathbb {R}$
.
$\mathbb {R}$
.
Even in this setting and for a symplectic twist diffeomorphism of the two-dimensional annulus
![]() $\mathbb {A}=\mathbb {T}\times \mathbb {R}$
, there exist results in which the authors are able to prove the existence of such an invariant continuous foliation by curves that are graphs (see, for example, [Reference Cheng and Sun5] or [Reference Florio and Le Calvez8]) but not able to say more (e.g. to describe the dynamics or prove that the foliation is symplectically straightenable). Observe too that the case of a Tonelli Hamiltonian with two degrees of freedom corresponds to the case of twist maps by using a Poincaré section close to some invariant torus in an energy surface, and that in this setting also the same questions are open and relevant (see, for example, [Reference Massart and Sorrentino15]).
$\mathbb {A}=\mathbb {T}\times \mathbb {R}$
, there exist results in which the authors are able to prove the existence of such an invariant continuous foliation by curves that are graphs (see, for example, [Reference Cheng and Sun5] or [Reference Florio and Le Calvez8]) but not able to say more (e.g. to describe the dynamics or prove that the foliation is symplectically straightenable). Observe too that the case of a Tonelli Hamiltonian with two degrees of freedom corresponds to the case of twist maps by using a Poincaré section close to some invariant torus in an energy surface, and that in this setting also the same questions are open and relevant (see, for example, [Reference Massart and Sorrentino15]).
Definition. A map
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is
$f:\mathbb {A}\rightarrow \mathbb {A}$
is
![]() $C^0$
-integrable if f has an invariant
$C^0$
-integrable if f has an invariant
![]() $C^0$
-foliation by graphs.
$C^0$
-foliation by graphs.
For such a foliation by graphs of
![]() $\theta \in \mathbb {T}\mapsto \eta _c(\theta )\in \mathbb {R}$
where
$\theta \in \mathbb {T}\mapsto \eta _c(\theta )\in \mathbb {R}$
where
![]() $\int _{\mathbb {T}}\eta _c(\theta )=c$
, we introduce what we call its generating function, that is,
$\int _{\mathbb {T}}\eta _c(\theta )=c$
, we introduce what we call its generating function, that is,
![]() $u:\mathbb {A}\rightarrow \mathbb {R}$
defined by
$u:\mathbb {A}\rightarrow \mathbb {R}$
defined by
 $$ \begin{align*}u(\theta, c)=\int_0^\theta (\eta_c(t)-c)\,dt.\end{align*} $$
$$ \begin{align*}u(\theta, c)=\int_0^\theta (\eta_c(t)-c)\,dt.\end{align*} $$
(This terminology will be better understood when we will introduce the generating functions of a large class of symplectic homeomorphisms. Let us mention that for a general foliation, the generating function of the foliation is not necessarily the generating function of a symplectic homeomorphism. We will later give conditions for this to be true.)
Definition. Let
![]() ${\mathcal F}$
be a continuous foliation of
${\mathcal F}$
be a continuous foliation of
![]() $\mathbb {A}$
into graphs. Then the unique continuous function
$\mathbb {A}$
into graphs. Then the unique continuous function
![]() $u:\mathbb {A}\rightarrow \mathbb {R}$
that is
$u:\mathbb {A}\rightarrow \mathbb {R}$
that is
![]() $C^1$
with respect to the
$C^1$
with respect to the
![]() $\mathbb {T}$
variable such that
$\mathbb {T}$
variable such that
-
•
 $\text {for all } c\in \mathbb {R}, u(0, c)=0$
,
$\text {for all } c\in \mathbb {R}, u(0, c)=0$
, -
•
 $\text {for all } c\in \mathbb {R}$
, the graph of
$\text {for all } c\in \mathbb {R}$
, the graph of
 $c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of
$c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of
 ${\mathcal F}$
,
${\mathcal F}$
,
is called the generating function of
![]() ${\mathcal F}$
.
${\mathcal F}$
.
Our first result proves that in the
![]() $C^0$
integrable case of twist diffeomorphisms, there is more regularity of the generating function giving the foliation than we should expect.
$C^0$
integrable case of twist diffeomorphisms, there is more regularity of the generating function giving the foliation than we should expect.
Theorem 1.1. Let
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
be a
$f:\mathbb {A}\rightarrow \mathbb {A}$
be a
![]() $C^1$
symplectic twist diffeomorphism. When f is
$C^1$
symplectic twist diffeomorphism. When f is
![]() $C^0$
integrable, the generating function u of its invariant foliation is
$C^0$
integrable, the generating function u of its invariant foliation is
![]() $C^1$
.
$C^1$
.
Moreover, in this case, we have (see the notation
![]() $\pi _1$
at the beginning of §1.2), for all
$\pi _1$
at the beginning of §1.2), for all
![]() $c\in \mathbb {R}$
, that:
$c\in \mathbb {R}$
, that:
-
• the graph of
 $c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of the invariant foliation;
$c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of the invariant foliation; -
•
 $h_c:\theta \mapsto \theta +({\partial u}/{\partial c})(\theta ,c)$
is a semi-conjugacy between the projected dynamics
$h_c:\theta \mapsto \theta +({\partial u}/{\partial c})(\theta ,c)$
is a semi-conjugacy between the projected dynamics
 $g_c: \theta \mapsto \pi _1\circ f(\theta , c+({\partial u}/{\partial \theta })(\theta ,c))$
and a rotation R of
$g_c: \theta \mapsto \pi _1\circ f(\theta , c+({\partial u}/{\partial \theta })(\theta ,c))$
and a rotation R of
 $\mathbb {T}$
, that is,
$\mathbb {T}$
, that is,
 $h_{c}\circ g_c=R\circ h_{c}.$
$h_{c}\circ g_c=R\circ h_{c}.$
This allows us to give an example of a foliation of the annulus into smooth graphs that cannot be invariant by a
![]() $C^0$
-integrable symplectic twist diffeomorphism. But we will see in §7 that it can be invariant by an exact symplectic twist homeomorphism that is a
$C^0$
-integrable symplectic twist diffeomorphism. But we will see in §7 that it can be invariant by an exact symplectic twist homeomorphism that is a
![]() $C^1$
-diffeomorphism.
$C^1$
-diffeomorphism.
Corollary 1.1. Let
![]() $\varepsilon :\mathbb {R}\rightarrow \mathbb {R}$
be a non-
$\varepsilon :\mathbb {R}\rightarrow \mathbb {R}$
be a non-
![]() $C^1$
function that is k-Lipschitz for some
$C^1$
function that is k-Lipschitz for some
![]() $k<1$
. Then the function
$k<1$
. Then the function
is the generating function of a foliation of
![]() $\mathbb {A}$
into smooth graphs of
$\mathbb {A}$
into smooth graphs of
![]() $\theta \in \mathbb {T}\mapsto c+\varepsilon (c)\cos (2\pi \theta )$
that is not invariant by any
$\theta \in \mathbb {T}\mapsto c+\varepsilon (c)\cos (2\pi \theta )$
that is not invariant by any
![]() $C^0$
-integrable symplectic twist
$C^0$
-integrable symplectic twist
![]() $(C^1)$
diffeomorphism.
$(C^1)$
diffeomorphism.
The striking fact is the regularity in c. Indeed, if we have a
![]() $C^k$
foliation in graphs for some
$C^k$
foliation in graphs for some
![]() $k\geq 1$
, we can only claim that u and
$k\geq 1$
, we can only claim that u and
![]() ${\partial u}/{\partial \theta }$
are
${\partial u}/{\partial \theta }$
are
![]() $C^k$
. So in the
$C^k$
. So in the
![]() $C^0$
case, even the derivability with respect to c, which is a result of the invariance by a symplectic twist diffeomorphism, is surprising. Also, the fact that the semi-conjugacy
$C^0$
case, even the derivability with respect to c, which is a result of the invariance by a symplectic twist diffeomorphism, is surprising. Also, the fact that the semi-conjugacy
![]() $h_c$
continuously depends on c even at a c where the rotation number is rational is very surprising. At an irrational rotation number, this is an easy consequence of the uniqueness of the invariant measure supported on the corresponding leaf, but what happens for a rational rotation number is more subtle.
$h_c$
continuously depends on c even at a c where the rotation number is rational is very surprising. At an irrational rotation number, this is an easy consequence of the uniqueness of the invariant measure supported on the corresponding leaf, but what happens for a rational rotation number is more subtle.
Another result for
![]() $C^0$
-integrable twist diffeomorphisms is that the invariant foliation is not only
$C^0$
-integrable twist diffeomorphisms is that the invariant foliation is not only
![]() $C^0$
but also
$C^0$
but also
![]() $\tfrac 12$
-Hölder. It has been well known since Birkhoff that it is locally uniformly Lipschitz in the variable
$\tfrac 12$
-Hölder. It has been well known since Birkhoff that it is locally uniformly Lipschitz in the variable
![]() $\theta $
, and we prove here some regularity with respect to c.
$\theta $
, and we prove here some regularity with respect to c.
Theorem 1.2. Let
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
be a
$f:\mathbb {A}\rightarrow \mathbb {A}$
be a
![]() $C^1$
symplectic twist diffeomorphism that is
$C^1$
symplectic twist diffeomorphism that is
![]() $C^0$
integrable with generating function u of its invariant foliation. Then on every compact subset of
$C^0$
integrable with generating function u of its invariant foliation. Then on every compact subset of
![]() $\mathbb {A}$
, the foliation
$\mathbb {A}$
, the foliation
![]() $(\theta ,c)\mapsto \eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)$
is uniformly
$(\theta ,c)\mapsto \eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)$
is uniformly
![]() $\tfrac 12$
-Hölder in the variable c.
$\tfrac 12$
-Hölder in the variable c.
In the
![]() $C^0$
-integrable case, the dynamics restricted to a leaf with a rational rotation number is completely periodic.
$C^0$
-integrable case, the dynamics restricted to a leaf with a rational rotation number is completely periodic.
It is an open question whether there can be a Denjoy counter-example when restricted to a leaf with an irrational rotation number.
With the notation of Theorem 1.1, let us observe that when
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is
$f:\mathbb {A}\rightarrow \mathbb {A}$
is
![]() $C^0$
integrable, there exists a dense
$C^0$
integrable, there exists a dense
![]() $G_\delta $
subset
$G_\delta $
subset
![]() ${\mathcal G}$
of
${\mathcal G}$
of
![]() $\mathbb {R}$
such that for every
$\mathbb {R}$
such that for every
![]() $c\in {\mathcal G}$
, the dynamics restricted to the graph of
$c\in {\mathcal G}$
, the dynamics restricted to the graph of
![]() $\eta _c$
is minimal. Indeed, the set
$\eta _c$
is minimal. Indeed, the set
![]() ${\mathcal R}$
of recurrent points is a
${\mathcal R}$
of recurrent points is a
![]() $G_\delta $
set with full Lebesgue measure, hence
$G_\delta $
set with full Lebesgue measure, hence
![]() ${\mathcal R}$
is dense. Hence there exists a dense
${\mathcal R}$
is dense. Hence there exists a dense
![]() $G_\delta $
subset
$G_\delta $
subset
![]() $G_1$
of
$G_1$
of
![]() $\mathbb {R}$
such that for every
$\mathbb {R}$
such that for every
![]() $c\in G_1$
, the set
$c\in G_1$
, the set
![]() $\{ \theta \in \mathbb {T}, (\theta , \eta _c(\theta ))\text { is recurrent}\}$
is a dense
$\{ \theta \in \mathbb {T}, (\theta , \eta _c(\theta ))\text { is recurrent}\}$
is a dense
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $\mathbb {T}$
. Hence, for
$\mathbb {T}$
. Hence, for
![]() $c\in G_1$
, the dynamics restricted to the graph of
$c\in G_1$
, the dynamics restricted to the graph of
![]() $\eta _c$
cannot be Denjoy. If we remove from
$\eta _c$
cannot be Denjoy. If we remove from
![]() $G_1$
the countable set of cs that correspond to a rational rotation number, we obtain a dense
$G_1$
the countable set of cs that correspond to a rational rotation number, we obtain a dense
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $\mathbb {R}$
such that the dynamics
$\mathbb {R}$
such that the dynamics
![]() $f_{\vert \text {Graph}{(}c+({\partial u}/{\partial \theta })(\cdot , c){)}} $
is minimal.
$f_{\vert \text {Graph}{(}c+({\partial u}/{\partial \theta })(\cdot , c){)}} $
is minimal.
We will give some conditions that imply that the dynamics restricted to a leaf cannot be Denjoy.
Before this, we need to explain the notion of straightenable foliation.
Notation. We will work in some open subsets
![]() ${\mathcal U}$
,
${\mathcal U}$
,
![]() ${\mathcal V}$
of either
${\mathcal V}$
of either
![]() $\mathbb {A}$
or
$\mathbb {A}$
or
![]() $\mathbb {R}^2$
, on which we have global symplectic coordinates that we denote by
$\mathbb {R}^2$
, on which we have global symplectic coordinates that we denote by
![]() $(\theta , r)$
or
$(\theta , r)$
or
![]() $(\theta , c)$
. Moreover, we will assume that:
$(\theta , c)$
. Moreover, we will assume that:
-
•
 ${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and } a(\theta )<r<b(\theta )\}$
or
${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and } a(\theta )<r<b(\theta )\}$
or
 ${\mathcal V}=\mathbb {A}$
where
${\mathcal V}=\mathbb {A}$
where
 $a, b$
are continuous functions defined on
$a, b$
are continuous functions defined on
 $[\alpha , \beta ]$
and
$[\alpha , \beta ]$
and
 $0\in (\alpha , \beta )$
;
$0\in (\alpha , \beta )$
; -
•
 ${\mathcal U}=\{(x,c); c\in (c_-, c_+) \text { and } d(c)< x< e(c)\}$
or
${\mathcal U}=\{(x,c); c\in (c_-, c_+) \text { and } d(c)< x< e(c)\}$
or
 ${\mathcal U}=\mathbb {A}$
where
${\mathcal U}=\mathbb {A}$
where
 $d, e$
are continuous functions defined on
$d, e$
are continuous functions defined on
 $[c_-, c_+]$
.
$[c_-, c_+]$
.
With this notation,
![]() $\partial ^+{\mathcal U}=[d(c_+), e(c_+)]\times \{ c_+\}$
(respectively,
$\partial ^+{\mathcal U}=[d(c_+), e(c_+)]\times \{ c_+\}$
(respectively,
![]() $\partial ^-{\mathcal U}=[d(c_-), e(c_-)]\times \{ c_-\}$
) is the upper (respectively, lower) boundary of
$\partial ^-{\mathcal U}=[d(c_-), e(c_-)]\times \{ c_-\}$
) is the upper (respectively, lower) boundary of
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() $\partial ^+{\mathcal V}=\{ (t, b(t)); t\in [\alpha , \beta ]\}$
(respectively,
$\partial ^+{\mathcal V}=\{ (t, b(t)); t\in [\alpha , \beta ]\}$
(respectively,
![]() $\partial ^-{\mathcal V}=\{ (t, a(t)); t\in [\alpha , \beta ]\}$
) is the upper (respectively, lower) boundary of
$\partial ^-{\mathcal V}=\{ (t, a(t)); t\in [\alpha , \beta ]\}$
) is the upper (respectively, lower) boundary of
![]() ${\mathcal V}$
.
${\mathcal V}$
.
Whenever
![]() ${\mathcal U}$
appears, the hypotheses will have as a consequence that
${\mathcal U}$
appears, the hypotheses will have as a consequence that
![]() ${\mathcal U}$
(respectively,
${\mathcal U}$
(respectively,
![]() $\overline {{\mathcal U}}$
) will be homeomorphic to
$\overline {{\mathcal U}}$
) will be homeomorphic to
![]() ${\mathcal V}$
(respectively,
${\mathcal V}$
(respectively,
![]() $\overline {{\mathcal V}}$
) and foliated by horizontal lines. In particular,
$\overline {{\mathcal V}}$
) and foliated by horizontal lines. In particular,
![]() ${\mathcal U}$
will always be homeomorphic to a disc or to an annulus. Firstly, we introduce the notion of exact symplectic homeomorphism, which is a particular case of the notion of symplectic homeomorphism that is due to Oh and Müller [Reference Oh and Müller18]. Their notion coincides in this two-dimensional setting with that of orientation- and Lebesgue measure-preserving homeomorphisms.
${\mathcal U}$
will always be homeomorphic to a disc or to an annulus. Firstly, we introduce the notion of exact symplectic homeomorphism, which is a particular case of the notion of symplectic homeomorphism that is due to Oh and Müller [Reference Oh and Müller18]. Their notion coincides in this two-dimensional setting with that of orientation- and Lebesgue measure-preserving homeomorphisms.
Definition. An exact symplectic homeomorphism from
![]() $\mathbb {A}$
onto
$\mathbb {A}$
onto
![]() $\mathbb {A}$
is a homeomorphism that is the limit for the
$\mathbb {A}$
is a homeomorphism that is the limit for the
![]() $C^0$
compact-open topology of a sequence of exact symplectic diffeomorphisms. (We recall that a diffeomorphism
$C^0$
compact-open topology of a sequence of exact symplectic diffeomorphisms. (We recall that a diffeomorphism
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is exact symplectic if the 1-form
$f:\mathbb {A}\rightarrow \mathbb {A}$
is exact symplectic if the 1-form
![]() $f^*(rd\theta )-rd\theta $
is exact.)
$f^*(rd\theta )-rd\theta $
is exact.)
A homeomorphism
![]() $\phi :{\mathcal U}\rightarrow {\mathcal V}$
is exact symplectic if there is a sequence
$\phi :{\mathcal U}\rightarrow {\mathcal V}$
is exact symplectic if there is a sequence
![]() $(\phi _n)_{n\in \mathbb {N}}$
of exact symplectic diffeomorphisms
$(\phi _n)_{n\in \mathbb {N}}$
of exact symplectic diffeomorphisms
![]() $\phi _n:{\mathcal U}\hookrightarrow {\mathcal V}$
such that the sequence
$\phi _n:{\mathcal U}\hookrightarrow {\mathcal V}$
such that the sequence
![]() $(\phi _n)$
converges to
$(\phi _n)$
converges to
![]() $\phi $
for the
$\phi $
for the
![]() $C^0$
compact-open topology.
$C^0$
compact-open topology.
Remark.
-
• In
 $\mathbb {R}^2$
, every 1-form is exact and then the notions of symplectic homeomorphism and exact symplectic homeomorphism coincide.
$\mathbb {R}^2$
, every 1-form is exact and then the notions of symplectic homeomorphism and exact symplectic homeomorphism coincide. -
• Let us recall that a symplectic diffeomorphism f of
 $\mathbb {A}$
that is isotopic to the identity is exact symplectic if and only if for every essential (an essential curve is a simple closed curve that is not homotopic to a point) curve
$\mathbb {A}$
that is isotopic to the identity is exact symplectic if and only if for every essential (an essential curve is a simple closed curve that is not homotopic to a point) curve
 $\gamma $
of the annulus, the algebraic area between
$\gamma $
of the annulus, the algebraic area between
 $\gamma $
and
$\gamma $
and
 $f(\gamma )$
is zero.
$f(\gamma )$
is zero.
A remarkable tool can be associated to the exact symplectic homeomorphisms that map the standard horizontal foliation onto a foliation that is transverse to the vertical one. This is called a generating function.
Theorem 1.3. (And definition)
Recall that
![]() ${\mathcal U}$
,
${\mathcal U}$
,
![]() ${\mathcal V}$
are open subsets of either
${\mathcal V}$
are open subsets of either
![]() $\mathbb {A}$
or
$\mathbb {A}$
or
![]() $\mathbb {R}^2$
. Moreover,
$\mathbb {R}^2$
. Moreover,
![]() ${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta ) \text { and } a(\theta )<r<b(\theta )\}$
or
${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta ) \text { and } a(\theta )<r<b(\theta )\}$
or
![]() ${\mathcal V}=\mathbb {A}$
where
${\mathcal V}=\mathbb {A}$
where
![]() $a, b$
are continuous functions and
$a, b$
are continuous functions and
![]() $0\in (\alpha , \beta )$
and
$0\in (\alpha , \beta )$
and
![]() ${\mathcal U}=\{(x,c); c\in (c_-, c_+)\text { and } d(c)< x< e(c)\}$
or
${\mathcal U}=\{(x,c); c\in (c_-, c_+)\text { and } d(c)< x< e(c)\}$
or
![]() ${\mathcal U}=\mathbb {A}$
where
${\mathcal U}=\mathbb {A}$
where
![]() $d, e$
are continuous functions. We use the notation
$d, e$
are continuous functions. We use the notation
Then
![]() ${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
or
${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
or
![]() ${\mathcal W}=\mathbb {A}$
.
${\mathcal W}=\mathbb {A}$
.
Let
![]() $\Phi :{\mathcal U}\rightarrow {\mathcal V}$
be an exact symplectic homeomorphism that maps the standard horizontal foliation onto a foliation
$\Phi :{\mathcal U}\rightarrow {\mathcal V}$
be an exact symplectic homeomorphism that maps the standard horizontal foliation onto a foliation
![]() ${\mathcal F}$
that is transverse to the vertical one and that preserves the orientation of the leaves (here we mean the orientation projected on the horizontal foliation). Assume that
${\mathcal F}$
that is transverse to the vertical one and that preserves the orientation of the leaves (here we mean the orientation projected on the horizontal foliation). Assume that
![]() $\Phi $
extends to a homeomorphism
$\Phi $
extends to a homeomorphism
![]() $\overline {\Phi } : \overline {{\mathcal U}}\to \overline {{\mathcal V}}$
and that
$\overline {\Phi } : \overline {{\mathcal U}}\to \overline {{\mathcal V}}$
and that
![]() $\overline {\Phi }(\partial ^\pm {\mathcal U})=\partial ^\pm {\mathcal V}$
(this implies that the endpoints of the leaves of
$\overline {\Phi }(\partial ^\pm {\mathcal U})=\partial ^\pm {\mathcal V}$
(this implies that the endpoints of the leaves of
![]() ${\mathcal F}$
are not in
${\mathcal F}$
are not in
![]() $\partial ^\pm {\mathcal V}$
and then that all the leaves of
$\partial ^\pm {\mathcal V}$
and then that all the leaves of
![]() ${\mathcal F}$
are graphs above
${\mathcal F}$
are graphs above
![]() $(\alpha , \beta )$
).
$(\alpha , \beta )$
).
Then there exists a
![]() $C^1$
function
$C^1$
function
![]() $u:{\mathcal W}\rightarrow \mathbb {R}$
such that
$u:{\mathcal W}\rightarrow \mathbb {R}$
such that
In particular, when defined, every map
![]() $\theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
is injective and every set
$\theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
is injective and every set
![]() $\{(\theta , c+({\partial u}/{\partial \theta })(\theta , c)); \theta \in I\}$
is a leaf of the image of the standard horizontal foliation
$\{(\theta , c+({\partial u}/{\partial \theta })(\theta , c)); \theta \in I\}$
is a leaf of the image of the standard horizontal foliation
![]() $($
where
$($
where
![]() $I=\mathbb {T}$
or
$I=\mathbb {T}$
or
![]() $I=(\alpha , \beta ))$
.
$I=(\alpha , \beta ))$
.
The function u is called a generating function for
![]() $\Phi $
.
$\Phi $
.
Conversely, we consider a
![]() $C^0$
-foliation of
$C^0$
-foliation of
![]() ${\mathcal V}$
into graphs
${\mathcal V}$
into graphs
![]() $\eta _c:\mathbb {T}\rightarrow \mathbb {R}$
or
$\eta _c:\mathbb {T}\rightarrow \mathbb {R}$
or
![]() $\eta _c:(\alpha , \beta )~\rightarrow ~\mathbb {R}$
for
$\eta _c:(\alpha , \beta )~\rightarrow ~\mathbb {R}$
for
![]() $c\in J$
and assume that there exists a
$c\in J$
and assume that there exists a
![]() $C^1$
map
$C^1$
map
![]() $u : {{\mathcal W}} \to \mathbb {R}$
such that:
$u : {{\mathcal W}} \to \mathbb {R}$
such that:
-
•
 $u(0,c) = 0$
for all
$u(0,c) = 0$
for all
 $c\in J$
;
$c\in J$
; -
• the graph of
 $\theta \mapsto c+ ({\partial u}/{\partial \theta })(\theta ,c)$
defines a leaf of the original foliation;
$\theta \mapsto c+ ({\partial u}/{\partial \theta })(\theta ,c)$
defines a leaf of the original foliation; -
• for all
 $c\in J$
, the map
$c\in J$
, the map
 $\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
is increasing.
$\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
is increasing.
Then
defines an exact symplectic homeomorphism from
![]() ${\mathcal U}$
onto
${\mathcal U}$
onto
![]() ${\mathcal V}$
that maps the standard horizontal foliation onto the original foliation.
${\mathcal V}$
that maps the standard horizontal foliation onto the original foliation.
Corollary 1.2. The foliation given in Corollary 1.1 cannot be straightened via an exact symplectic homeomorphism that preserves the horizontal orientation of the leaves.
With some extra hypothesis and work we also obtain the following result.
Corollary 1.3. Assuming that the function
![]() $\varepsilon $
is not derivable on a dense set, the foliation given in Corollary 1.1 cannot be locally straightened via an exact symplectic homeomorphism that preserves the horizontal orientation of the leaves.
$\varepsilon $
is not derivable on a dense set, the foliation given in Corollary 1.1 cannot be locally straightened via an exact symplectic homeomorphism that preserves the horizontal orientation of the leaves.
Remarks.
-
(1) The formulas of Theorem 1.3 can be also written as
 $$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
$$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
-
(2) Observe that Theorem 1.1 gives us a
 $C^1$
function u, but not the injectivity of
$C^1$
function u, but not the injectivity of
 $\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
. This is why a priori the maps
$\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
. This is why a priori the maps
 $h_c$
are not conjugacies, but only semi-conjugacies and in this case the restricted dynamics may be Denjoy.
$h_c$
are not conjugacies, but only semi-conjugacies and in this case the restricted dynamics may be Denjoy.
We will now give a condition that implies that a foliation is straightenable by an exact symplectic homeomorphism.
Definition.
-
• A foliation by graphs
 $a\mapsto \eta _a$
is a Lipschitz foliation if
$a\mapsto \eta _a$
is a Lipschitz foliation if
 $(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a homeomorphism that is locally bi-Lipschitz.
$(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a homeomorphism that is locally bi-Lipschitz. -
• If f has an invariant Lipschitz foliation, f is Lipschitz integrable.
The following proposition is a consequence of Theorem 1.3 and results of Minguzzi on the mixed derivative [Reference Minguzzi16].
Proposition 1.1. Let
![]() $u:\mathbb {A}\rightarrow \mathbb {R}$
be the generating function of a continuous foliation of
$u:\mathbb {A}\rightarrow \mathbb {R}$
be the generating function of a continuous foliation of
![]() $\mathbb {A}$
into graphs. We assume that u is
$\mathbb {A}$
into graphs. We assume that u is
![]() $C^1$
. Then the two following assertions are equivalent.
$C^1$
. Then the two following assertions are equivalent.
-
(1) The foliation is Lipschitz.
-
(2) We have:
-
•
 ${\partial u}/{\partial \theta }$
is locally Lipschitz continuous;
${\partial u}/{\partial \theta }$
is locally Lipschitz continuous; -
•
 ${\partial u}/{\partial c}$
is uniformly Lipschitz continuous in the variable
${\partial u}/{\partial c}$
is uniformly Lipschitz continuous in the variable
 $\theta $
on any compact set of cs;
$\theta $
on any compact set of cs; -
• for every compact subset
 ${\mathcal K}\subset \mathbb {A}$
, there exist two constants
${\mathcal K}\subset \mathbb {A}$
, there exist two constants
 $k_+>k_->-1$
such that
$k_+>k_->-1$
such that
 $k_+\geq {\partial ^2 u}/{\partial \theta \partial c}\geq k_-$
Lebesgue almost everywhere in
$k_+\geq {\partial ^2 u}/{\partial \theta \partial c}\geq k_-$
Lebesgue almost everywhere in
 ${\mathcal K}$
.
${\mathcal K}$
.
-
In this case, u is the generating function of an exact symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one.
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one.
Observe that Corollary 1.2 gives an example of a Lipschitz foliation by smooth curves that is not straightenable via a symplectic homeomorphism. Hence the hypothesis that u is
![]() $C^1$
is crucial in Proposition 1.1.
$C^1$
is crucial in Proposition 1.1.
Definition.
-
• A map
 $a\mapsto \eta _a$
defines a
$a\mapsto \eta _a$
defines a
 $C^k$
foliation if
$C^k$
foliation if
 $(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a
$(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a
 $C^k$
diffeomorphism. If f has an invariant
$C^k$
diffeomorphism. If f has an invariant
 $C^k$
foliation, f is
$C^k$
foliation, f is
 $C^k$
integrable.
$C^k$
integrable. -
• Following [Reference Hirsch, Pugh and Shub11], a map
 $a\mapsto \eta _a$
defines a
$a\mapsto \eta _a$
defines a
 $C^k$
lamination if
$C^k$
lamination if
 $(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a homeomorphism, every
$(\theta , a)\mapsto (\theta , \eta _a(\theta ))$
is a homeomorphism, every
 $\eta _a$
is
$\eta _a$
is
 $C^k$
and the map
$C^k$
and the map
 $a\mapsto \eta _a$
is continuous when
$a\mapsto \eta _a$
is continuous when
 $C^k(\mathbb {T}, \mathbb {R})$
is endowed with the
$C^k(\mathbb {T}, \mathbb {R})$
is endowed with the
 $C^k$
topology.
$C^k$
topology.
Corollary 1.4. Let
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $r\mapsto f_r$
be a
$r\mapsto f_r$
be a
![]() $C^k$
-foliation in graphs. Then there exists a
$C^k$
-foliation in graphs. Then there exists a
![]() $C^{k-1}$
exact symplectic diffeomorphism (a
$C^{k-1}$
exact symplectic diffeomorphism (a
![]() $C^0$
diffeomorphism is a homeomorphism)
$C^0$
diffeomorphism is a homeomorphism)
![]() $\Phi : (\theta ,r ) \mapsto (h(\theta ,r) , \eta ( h(\theta ,r), r) )$
such that for each
$\Phi : (\theta ,r ) \mapsto (h(\theta ,r) , \eta ( h(\theta ,r), r) )$
such that for each
![]() $r\in \mathbb {R}$
, the set
$r\in \mathbb {R}$
, the set
![]() $\{ (\theta ,\eta (\theta ,r)), \theta \in \mathbb {T}\}$
is a leaf of the foliation.
$\{ (\theta ,\eta (\theta ,r)), \theta \in \mathbb {T}\}$
is a leaf of the foliation.
When a symplectic homeomorphism preserves a symplectic foliation that is symplectically straightenable, the dynamics is very simple. Let us introduce the following notion before explaining this point.
Definition. If
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is a symplectic homeomorphism, we call
$f:\mathbb {A}\rightarrow \mathbb {A}$
is a symplectic homeomorphism, we call
![]() $C^0$
Arnol’d–Liouville coordinates a symplectic homeomorphism
$C^0$
Arnol’d–Liouville coordinates a symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
such that the standard foliation by graphs
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
such that the standard foliation by graphs
![]() $\mathbb {T}\times \{ c\}$
is invariant by
$\mathbb {T}\times \{ c\}$
is invariant by
![]() $\Phi ^{-1}\circ f\circ \Phi $
and
$\Phi ^{-1}\circ f\circ \Phi $
and
for some (continuous) function
![]() $\rho :\mathbb {R}\rightarrow \mathbb {R}$
.
$\rho :\mathbb {R}\rightarrow \mathbb {R}$
.
Proposition 1.2. Let
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic homeomorphism that preserves (each leaf of) a
$f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic homeomorphism that preserves (each leaf of) a
![]() $C^0$
-foliation
$C^0$
-foliation
![]() ${\mathcal F}$
. If the foliation is symplectically straightenable (by
${\mathcal F}$
. If the foliation is symplectically straightenable (by
![]() $\Phi : \mathbb {A} \to \mathbb {A}$
that maps the standard foliation
$\Phi : \mathbb {A} \to \mathbb {A}$
that maps the standard foliation
![]() ${\mathcal F}_0$
to
${\mathcal F}_0$
to
![]() ${\mathcal F}=\Phi ({\mathcal F}_0)$
), then the homeomorphism
${\mathcal F}=\Phi ({\mathcal F}_0)$
), then the homeomorphism
![]() $\Phi $
provides
$\Phi $
provides
![]() $C^0$
Arnol’d–Liouville coordinates.
$C^0$
Arnol’d–Liouville coordinates.
Corollary 1.5. A symplectic twist diffeomorphism
![]() $f: \mathbb {A} \to \mathbb {A}$
is
$f: \mathbb {A} \to \mathbb {A}$
is
![]() $C^0$
-integrable with the dynamics on each leaf conjugate to a rotation if and only if the invariant foliation is exact symplectically homeomorphic to the standard foliation. In this case, f admits global
$C^0$
-integrable with the dynamics on each leaf conjugate to a rotation if and only if the invariant foliation is exact symplectically homeomorphic to the standard foliation. In this case, f admits global
![]() $C^0$
Arnol’d–Liouville coordinates.
$C^0$
Arnol’d–Liouville coordinates.
In the case where the invariant foliation by a symplectic twist diffeomorphism is Lipschitz, we are in the case of Proposition 1.2 and so for every leaf, the restricted dynamics is not Denjoy.
Corollary 1.6. Let
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic twist diffeomorphism that is Lipschitz integrable. We denote by u the generating function of its invariant foliation. Then u is the generating function of an exact symplectic homeomorphism
$f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic twist diffeomorphism that is Lipschitz integrable. We denote by u the generating function of its invariant foliation. Then u is the generating function of an exact symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one such that
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one such that
where
![]() $\rho :\mathbb {R}\rightarrow \mathbb {R}$
is an increasing bi-Lipschitz homeomorphism.
$\rho :\mathbb {R}\rightarrow \mathbb {R}$
is an increasing bi-Lipschitz homeomorphism.
Moreover, the invariant foliation is a
![]() $C^1$
lamination and
$C^1$
lamination and
![]() $\Phi $
admits a partial derivative with respect to
$\Phi $
admits a partial derivative with respect to
![]() $\theta $
. The projected dynamics
$\theta $
. The projected dynamics
![]() $g_c$
restricted to every leaf is
$g_c$
restricted to every leaf is
![]() $C^1$
conjugate to a rotation via the
$C^1$
conjugate to a rotation via the
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h_c=Id_{\mathbb {T}}+({\partial u}/{\partial c})(\cdot , c):\mathbb {T}\rightarrow \mathbb {T}$
such that
$h_c=Id_{\mathbb {T}}+({\partial u}/{\partial c})(\cdot , c):\mathbb {T}\rightarrow \mathbb {T}$
such that
![]() $h_{c}\circ g_c=R\circ h_{c}$
.
$h_{c}\circ g_c=R\circ h_{c}$
.
Corollary 1.6 provides some
![]() $C^0$
Arnol’d–Liouville coordinates. A similar statement for Tonelli Hamiltonians is proved in [Reference Arnaud and Xue3], without the fact that the conjugation is
$C^0$
Arnol’d–Liouville coordinates. A similar statement for Tonelli Hamiltonians is proved in [Reference Arnaud and Xue3], without the fact that the conjugation is
![]() $C^1$
.
$C^1$
.
1.2 Some notation and definitions
We will use the following notation.
Notation.
-
•
 $\mathbb {T}=\mathbb {R}/\mathbb {Z}$
is the circle and
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$
is the circle and
 $\mathbb {A}=\mathbb {T}\times \mathbb {R}$
is the annulus;
$\mathbb {A}=\mathbb {T}\times \mathbb {R}$
is the annulus;
 $\pi : \mathbb {R}\rightarrow \mathbb {T}$
is the usual projection.
$\pi : \mathbb {R}\rightarrow \mathbb {T}$
is the usual projection. -
• The universal covering of the annulus is denoted by
 $p:\mathbb {R}^2\rightarrow \mathbb {A}$
.
$p:\mathbb {R}^2\rightarrow \mathbb {A}$
. -
• The corresponding projections are
 $\pi _1: (\theta , r)\in \mathbb {A}\mapsto \theta \in \mathbb {T}$
and
$\pi _1: (\theta , r)\in \mathbb {A}\mapsto \theta \in \mathbb {T}$
and
 $\pi _2: (\theta , r)\in \mathbb {A}\mapsto r~\in ~\mathbb {R}$
; we denote also the corresponding projections of the universal covering by
$\pi _2: (\theta , r)\in \mathbb {A}\mapsto r~\in ~\mathbb {R}$
; we denote also the corresponding projections of the universal covering by
 $\pi _1$
,
$\pi _1$
,
 $\pi _2~: \mathbb {R}^2\rightarrow \mathbb {R}$
.
$\pi _2~: \mathbb {R}^2\rightarrow \mathbb {R}$
. -
• The Liouville 1-form is defined on
 $\mathbb {A}$
as being
$\mathbb {A}$
as being
 $\lambda =\pi _2d\pi _1=rd\theta $
; then
$\lambda =\pi _2d\pi _1=rd\theta $
; then
 $\mathbb {A}$
is endowed with the symplectic form
$\mathbb {A}$
is endowed with the symplectic form
 $\omega =-d\lambda $
.
$\omega =-d\lambda $
.
Let us recall the definition of a symplectic twist diffeomorphism.
Definition. A symplectic twist diffeomorphism
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is a
$f:\mathbb {A}\rightarrow \mathbb {A}$
is a
![]() $C^1$
diffeomorphism such that:
$C^1$
diffeomorphism such that:
-
• f is isotopic to the identity;
-
• f is symplectic, that is,
 $f^*\omega =\omega $
;
$f^*\omega =\omega $
; -
• f has the twist property, that is,
 $F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f;
$F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f; -
• for any
 $\tilde \theta \in \mathbb {R}$
, the map
$\tilde \theta \in \mathbb {R}$
, the map
 $r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing
$r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing
 $C^1$
diffeomorphism from
$C^1$
diffeomorphism from
 $\mathbb {R}$
onto
$\mathbb {R}$
onto
 $\mathbb {R}$
.
$\mathbb {R}$
.
1.3 Content of the different sections
The main tools that we will use are tools of ergodic theory and symplectic (continuous or differentiable) dynamics, in particular symplectic twist maps and Green bundles. The rest of the paper is organized as follows.
-
• Section 2 contains the proof of Theorem 1.1. After recalling some generalities about symplectic twist diffeomorphisms, we consider the case of rational curves by using some ergodic theory. Then we prove the regularity of u also by using ergodic theory.
-
• Section 5 contains the proofs of Proposition 1.1 and Corollary 1.4.
-
• Section 6 contains the proofs of Proposition 1.2, Corollaries 1.5 and 1.6.
-
• Section 7 introduces a strange foliation, provides the proofs of Corollaries 1.1 and 1.2 and an example of an exact symplectic twist map that leaves the strange foliation invariant.
-
• Appendix A contains an example of a foliation by graphs that is the inverse image of the standard foliation by a symplectic map but not by a symplectic homeomorphism. Appendix B recalls some results about Green bundles.
2 Proof of Theorem 1.1
We assume that
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is a
$f:\mathbb {A}\rightarrow \mathbb {A}$
is a
![]() $C^k$
symplectic twist diffeomorphism (with
$C^k$
symplectic twist diffeomorphism (with
![]() $k\geq 1$
) that has a continuous invariant foliation by continuous graphs with generating function denoted by u. We write
$k\geq 1$
) that has a continuous invariant foliation by continuous graphs with generating function denoted by u. We write
![]() $\eta _c=c+({\partial u}/{\partial \theta })(\cdot , c)$
and we recall that Birkhoff’s theorem (see [Reference Birkhoff4, Reference Fathi7, Reference Herman10]) implies that all the
$\eta _c=c+({\partial u}/{\partial \theta })(\cdot , c)$
and we recall that Birkhoff’s theorem (see [Reference Birkhoff4, Reference Fathi7, Reference Herman10]) implies that all the
![]() $\eta _c$
are Lipschitz.
$\eta _c$
are Lipschitz.
Notation. For every
![]() $c\in \mathbb {R}$
, we will denote by
$c\in \mathbb {R}$
, we will denote by
![]() $g_c:\mathbb {T}\rightarrow \mathbb {T}$
the restricted-projected dynamics to the graph of
$g_c:\mathbb {T}\rightarrow \mathbb {T}$
the restricted-projected dynamics to the graph of
![]() $\eta _c$
, that is,
$\eta _c$
, that is,
2.1 Some generalities
Notation.
-
• In
 $\mathbb {R}^2$
we denote by
$\mathbb {R}^2$
we denote by
 $B(x, r)$
the open disc for the usual Euclidean distance with centre x and radius r.
$B(x, r)$
the open disc for the usual Euclidean distance with centre x and radius r. -
• We denote by
 $R_\alpha :\mathbb {T}\rightarrow \mathbb {T}$
the rotation
$R_\alpha :\mathbb {T}\rightarrow \mathbb {T}$
the rotation
 $R_\alpha (\theta )=\theta +\alpha $
.
$R_\alpha (\theta )=\theta +\alpha $
. -
• If E is a finite set, then
 $\sharp (E)$
is the number of elements it contains.
$\sharp (E)$
is the number of elements it contains. -
• We denote by
 $\lfloor \cdot \rfloor : \mathbb {R}\rightarrow \mathbb {Z}$
the integer part.
$\lfloor \cdot \rfloor : \mathbb {R}\rightarrow \mathbb {Z}$
the integer part.
We fix a lift
![]() $F:\mathbb {R}^2\rightarrow \mathbb {R}^2$
of f. We denote by
$F:\mathbb {R}^2\rightarrow \mathbb {R}^2$
of f. We denote by
![]() $\tilde \eta _c:\mathbb {R}\rightarrow \mathbb {R}$
a lift of
$\tilde \eta _c:\mathbb {R}\rightarrow \mathbb {R}$
a lift of
![]() $\eta _c$
. We denote by
$\eta _c$
. We denote by
![]() $\rho $
the function that maps
$\rho $
the function that maps
![]() $c\in \mathbb {R}$
to the rotation number
$c\in \mathbb {R}$
to the rotation number
![]() $\rho (c)\in \mathbb {R}$
of the restriction of F to the graph of
$\rho (c)\in \mathbb {R}$
of the restriction of F to the graph of
![]() $\tilde \eta _c$
.
$\tilde \eta _c$
.
The map
![]() $\rho $
is then an increasing homeomorphism.
$\rho $
is then an increasing homeomorphism.
When the foliation is bi-Lipschitz, we will prove that
![]() $\rho $
is a bi-Lipschitz homeomorphism (see Proposition 6.1). We recall a well-known result concerning the link between invariant measures and semi-conjugacies for orientation-preserving homeomorphisms of
$\rho $
is a bi-Lipschitz homeomorphism (see Proposition 6.1). We recall a well-known result concerning the link between invariant measures and semi-conjugacies for orientation-preserving homeomorphisms of
![]() $\mathbb {T}$
.
$\mathbb {T}$
.
Proposition 2.1. Let
![]() $g:\mathbb {T}\rightarrow \mathbb {T}$
be an orientation-preserving homeomorphism. Assume that
$g:\mathbb {T}\rightarrow \mathbb {T}$
be an orientation-preserving homeomorphism. Assume that
![]() $\mu $
is a non-atomic Borel invariant probability measure by g. Then, if the rotation number
$\mu $
is a non-atomic Borel invariant probability measure by g. Then, if the rotation number
![]() $\rho $
of g is irrational or g is
$\rho $
of g is irrational or g is
![]() $C^0$
conjugate to a rotation, the map
$C^0$
conjugate to a rotation, the map
![]() $h:\mathbb {T}\rightarrow \mathbb {T}$
defined by
$h:\mathbb {T}\rightarrow \mathbb {T}$
defined by
![]() $h(\theta )=\int _0^\theta d\mu $
is a semi-conjugacy between g and the rotation of angle
$h(\theta )=\int _0^\theta d\mu $
is a semi-conjugacy between g and the rotation of angle
![]() $\rho $
, that is,
$\rho $
, that is,
Proof. Let
![]() $\tilde \mu $
be the pullback measure of
$\tilde \mu $
be the pullback measure of
![]() $\mu $
to
$\mu $
to
![]() $\mathbb {R}$
and let
$\mathbb {R}$
and let
![]() $\tilde g:\mathbb {R}\rightarrow \mathbb {R}$
be a lift of g to
$\tilde g:\mathbb {R}\rightarrow \mathbb {R}$
be a lift of g to
![]() $\mathbb {R}$
. Then we have, for every
$\mathbb {R}$
. Then we have, for every
![]() $\Theta \in [0, 1]$
lift of
$\Theta \in [0, 1]$
lift of
![]() $\theta \in \mathbb {T}$
,
$\theta \in \mathbb {T}$
,
where
![]() $\lfloor \tilde g(0)\rfloor $
is the integer part of
$\lfloor \tilde g(0)\rfloor $
is the integer part of
![]() $\tilde g(0)$
. This implies
$\tilde g(0)$
. This implies
(Recall that if
![]() $f : \mathbb {T} \to \mathbb {T}$
is an orientation-preserving homeomorphism then either
$f : \mathbb {T} \to \mathbb {T}$
is an orientation-preserving homeomorphism then either
![]() $\rho (f)$
is irrational, f is semi-conjugate (by h) to the rotation
$\rho (f)$
is irrational, f is semi-conjugate (by h) to the rotation
![]() $R_{\rho (f)}$
and the only invariant measure is the pullback of the Lebesgue measure by h; or
$R_{\rho (f)}$
and the only invariant measure is the pullback of the Lebesgue measure by h; or
![]() $\rho (f)$
is rational and the ergodic invariant measures are supported on periodic orbits. When
$\rho (f)$
is rational and the ergodic invariant measures are supported on periodic orbits. When
![]() $\rho (f)$
is irrational or when f is
$\rho (f)$
is irrational or when f is
![]() $C^0$
conjugate to a rotation and
$C^0$
conjugate to a rotation and
![]() $\rho (f)\in [0, 1[$
, then for any invariant measure
$\rho (f)\in [0, 1[$
, then for any invariant measure
![]() $\mu $
and
$\mu $
and
![]() $x\in \mathbb {T}$
,
$x\in \mathbb {T}$
,
![]() $\mu ([x,f(x)[) = \rho (f)$
.) Moreover, as we assumed that
$\mu ([x,f(x)[) = \rho (f)$
.) Moreover, as we assumed that
![]() $\mu $
is non-atomic, h is continuous.
$\mu $
is non-atomic, h is continuous.
Remarks.
-
(1) Conversely, if h is a (non-decreasing) semi-conjugacy such that
 $h\circ g=h+\rho $
, then
$h\circ g=h+\rho $
, then
 $\mu ([0, \theta ])=h(\theta )-h(0)$
defines a g-invariant Borel probability measure.
$\mu ([0, \theta ])=h(\theta )-h(0)$
defines a g-invariant Borel probability measure. -
(2) When
 $\rho $
is irrational, it is well known that the Borel invariant probability measure
$\rho $
is irrational, it is well known that the Borel invariant probability measure
 $\mu $
is unique and that the semi-conjugacy h is unique up to a constant.
$\mu $
is unique and that the semi-conjugacy h is unique up to a constant.
Notation. When
![]() $\rho (c)$
is irrational, we will denote by
$\rho (c)$
is irrational, we will denote by
![]() $h_c$
the semi-conjugacy such that
$h_c$
the semi-conjugacy such that
![]() $h_c(0)=0$
.
$h_c(0)=0$
.
Before entering the core of the proof, let us mention a useful fact about iterates of
![]() $C^0$
-integrable symplectic twist diffeomorphisms.
$C^0$
-integrable symplectic twist diffeomorphisms.
Proposition 2.2. Let
![]() $f: \mathbb {A} \to \mathbb {A}$
be a
$f: \mathbb {A} \to \mathbb {A}$
be a
![]() $C^0$
-integrable
$C^0$
-integrable
![]() $C^1$
symplectic twist diffeomorphism. Then so is
$C^1$
symplectic twist diffeomorphism. Then so is
![]() $f^n$
for all
$f^n$
for all
![]() $n>0$
.
$n>0$
.
This is specific to the integrable case: in general, an iterated twist diffeomorphism is not a twist diffeomorphism, as can be seen in the neighborhood of an elliptic fixed point.
Proof. We argue by induction on
![]() $n>0$
. The initialization being trivial, let us assume the result true for some
$n>0$
. The initialization being trivial, let us assume the result true for some
![]() $n>0$
. Let
$n>0$
. Let
![]() $F : \mathbb {R}^2 \to \mathbb {R}^2$
be a lift of f. For any
$F : \mathbb {R}^2 \to \mathbb {R}^2$
be a lift of f. For any
![]() $c\in \mathbb {R}$
, using the notation given at the beginning of §2, we have
$c\in \mathbb {R}$
, using the notation given at the beginning of §2, we have
Observe that if
![]() $f^m$
satisfies the twist condition and
$f^m$
satisfies the twist condition and
![]() $c_1<c_2$
are two real numbers, denoting by
$c_1<c_2$
are two real numbers, denoting by
![]() $\sim $
the lifts of the considered functions, then we have
$\sim $
the lifts of the considered functions, then we have
and
![]() ${\lim _{t\rightarrow \pm \infty }\tilde g_{c_1}(t)=\pm \infty }$
.
${\lim _{t\rightarrow \pm \infty }\tilde g_{c_1}(t)=\pm \infty }$
.
Let
![]() $c_1<c_2$
and
$c_1<c_2$
and
![]() $t\in \mathbb {R}$
. We obtain that
$t\in \mathbb {R}$
. We obtain that
 $$ \begin{align*}& \pi_1(F^{n+1}(t,\eta_{c_2}(t))) -\pi_1(F^{n+1}(t,\eta_{c_1}(t)))\\ &\quad = \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t)> \tilde g_{c_2}\circ \tilde g^{n}_{c_1}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t) ,\end{align*} $$
$$ \begin{align*}& \pi_1(F^{n+1}(t,\eta_{c_2}(t))) -\pi_1(F^{n+1}(t,\eta_{c_1}(t)))\\ &\quad = \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t)> \tilde g_{c_2}\circ \tilde g^{n}_{c_1}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t) ,\end{align*} $$
where we have used the induction hypothesis,
![]() $\tilde g^{n}_{c_2}(t)> \tilde g^{n}_{c_1}(t)$
, and the fact that
$\tilde g^{n}_{c_2}(t)> \tilde g^{n}_{c_1}(t)$
, and the fact that
![]() $\tilde g_{c_2}$
is increasing. It follows that
$\tilde g_{c_2}$
is increasing. It follows that
![]() $c\mapsto \pi _1(F^{n+1}(t,\eta _{c}(t))) $
is an increasing diffeomorphism onto its image. Observe also that this inequality implies that
$c\mapsto \pi _1(F^{n+1}(t,\eta _{c}(t))) $
is an increasing diffeomorphism onto its image. Observe also that this inequality implies that
because
![]() ${\lim _{c_2\rightarrow +\infty }\tilde g_{c_2}(s) =+\infty }$
. Moreover,
${\lim _{c_2\rightarrow +\infty }\tilde g_{c_2}(s) =+\infty }$
. Moreover,
 $$ \begin{align*}& \pi_1(F^{n+1}(t,\eta_{c_2}(t))) -\pi_1(F^{n+1}(t,\eta_{c_1}(t)))\\ &\quad = \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t) \leq \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_2}(t) \end{align*} $$
$$ \begin{align*}& \pi_1(F^{n+1}(t,\eta_{c_2}(t))) -\pi_1(F^{n+1}(t,\eta_{c_1}(t)))\\ &\quad = \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_1}(t) \leq \tilde g_{c_2}\circ \tilde g^{n}_{c_2}(t) -\tilde g_{c_1}\circ \tilde g^{n}_{c_2}(t) \end{align*} $$
implies that
![]() ${\lim _{c_1\rightarrow -\infty } \pi _1(F^{n+1}(t,\eta _{c_1}(t))) =-\infty }$
because
${\lim _{c_1\rightarrow -\infty } \pi _1(F^{n+1}(t,\eta _{c_1}(t))) =-\infty }$
because
![]() ${\lim _{c_1\rightarrow -\infty }\tilde g_{c_1}(s) =-\infty }$
. So finally
${\lim _{c_1\rightarrow -\infty }\tilde g_{c_1}(s) =-\infty }$
. So finally
![]() $c\mapsto \pi _1(F^{n+1}(t,\eta _{c}(t))) $
is an increasing diffeomorphism onto
$c\mapsto \pi _1(F^{n+1}(t,\eta _{c}(t))) $
is an increasing diffeomorphism onto
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
2.2 Differentiability and conjugacy along rational curves
It is proved in [Reference Arnaud1] that for every
![]() $r={p}/{q}\in \mathbb {Q}$
,
$r={p}/{q}\in \mathbb {Q}$
,
![]() $\eta _c=\eta _{\rho ^{-1}(r)}$
is
$\eta _c=\eta _{\rho ^{-1}(r)}$
is
![]() $C^k$
and the restriction of f to the graph
$C^k$
and the restriction of f to the graph
![]() $\Gamma _c$
of
$\Gamma _c$
of
![]() $\eta _c$
is completely periodic:
$\eta _c$
is completely periodic:
![]() $f^q_{\vert \Gamma _c}={\textrm {Id}}_{\Gamma _c}$
. Moreover, along these particular curves, the two Green bundles (see Appendix B for definition and results) are equal:
$f^q_{\vert \Gamma _c}={\textrm {Id}}_{\Gamma _c}$
. Moreover, along these particular curves, the two Green bundles (see Appendix B for definition and results) are equal:
Theorem 2.1.
-
• Along every leaf
 $\Gamma _c$
such that
$\Gamma _c$
such that
 $\rho (c)\in \mathbb {Q}$
, the derivative
$\rho (c)\in \mathbb {Q}$
, the derivative
 ${\partial \eta _c(\theta )}/{\partial c}=1+ ({\partial ^2u}/{\partial c\partial \theta })$
exists, is positive and
${\partial \eta _c(\theta )}/{\partial c}=1+ ({\partial ^2u}/{\partial c\partial \theta })$
exists, is positive and
 $C^{k-1}$
depends on
$C^{k-1}$
depends on
 $\theta $
.
$\theta $
. -
• For any c such that
 $\rho (c)$
is rational, the Borel probability measure
$\rho (c)$
is rational, the Borel probability measure
 $\mu _c$
on
$\mu _c$
on
 $\mathbb {T}$
of density
$\mathbb {T}$
of density
 ${\partial \eta _c}/{\partial c}$
is invariant by
${\partial \eta _c}/{\partial c}$
is invariant by
 $g_c$
and, for
$g_c$
and, for
 $\theta \in [0, 1]$
, the equality defines a conjugacy between
$\theta \in [0, 1]$
, the equality defines a conjugacy between $$ \begin{align*}h_c(\theta)=\mu_c([0, \theta])=\int_0^\theta \frac{\partial \eta_c}{\partial c}(t)\,dt\end{align*} $$
$$ \begin{align*}h_c(\theta)=\mu_c([0, \theta])=\int_0^\theta \frac{\partial \eta_c}{\partial c}(t)\,dt\end{align*} $$
 $g_c$
and the rotation with angle
$g_c$
and the rotation with angle
 $\rho (c)$
.
$\rho (c)$
.
-
• Then the map
 $c\in \mathbb {R}\mapsto \mu _c$
is continuous for the weak* topology on measures and
$c\in \mathbb {R}\mapsto \mu _c$
is continuous for the weak* topology on measures and
 $c\in \mathbb {R}\mapsto h_c$
is continuous for the uniform
$c\in \mathbb {R}\mapsto h_c$
is continuous for the uniform
 $C^0$
topology. Thus
$C^0$
topology. Thus
 $(\theta , c)\mapsto h_c(\theta )$
is continuous.
$(\theta , c)\mapsto h_c(\theta )$
is continuous.
Remarks.
-
(1) Observe that because
 $c\mapsto \eta _c$
is increasing, we know that for Lebesgue almost every
$c\mapsto \eta _c$
is increasing, we know that for Lebesgue almost every
 $(\theta , c)\in \mathbb {A}$
, the derivative
$(\theta , c)\in \mathbb {A}$
, the derivative
 ${\partial \eta _c(\theta )}/{\partial c}$
exists (see [Reference Kolmogorov and Fomine12]). But our theorem says something different.
${\partial \eta _c(\theta )}/{\partial c}$
exists (see [Reference Kolmogorov and Fomine12]). But our theorem says something different. -
(2) Because of the continuous dependence on
 $\theta $
along the rational curve, we obtain that
$\theta $
along the rational curve, we obtain that
 ${\partial \eta _c(\theta )}/{\partial c}$
restricted to every rational curve is bounded (this is clear when we assume that the foliation is Lipschitz but not if the foliation is just continuous).
${\partial \eta _c(\theta )}/{\partial c}$
restricted to every rational curve is bounded (this is clear when we assume that the foliation is Lipschitz but not if the foliation is just continuous).
Proof of the first point of Theorem 2.1. We fix
![]() $A\in \mathbb {R}$
such that
$A\in \mathbb {R}$
such that
![]() $\rho (A)={p}/{q}\in \mathbb {Q}$
. Replacing f by
$\rho (A)={p}/{q}\in \mathbb {Q}$
. Replacing f by
![]() $f^q$
, we can assume that
$f^q$
, we can assume that
![]() $\rho (A)\in \mathbb {Z}$
. Observe that because of the
$\rho (A)\in \mathbb {Z}$
. Observe that because of the
![]() $C^0$
-integrability of f,
$C^0$
-integrability of f,
![]() $f^q$
is also a
$f^q$
is also a
![]() $C^k$
symplectic twist diffeomorphism that is
$C^k$
symplectic twist diffeomorphism that is
![]() $C^0$
-integrable with the same invariant foliation (Proposition 2.2).
$C^0$
-integrable with the same invariant foliation (Proposition 2.2).
We define
![]() $G_A: \mathbb {A}\rightarrow \mathbb {A}$
by
$G_A: \mathbb {A}\rightarrow \mathbb {A}$
by
Then
![]() $G_A^{-1}\circ f^q\circ G_A$
is also a
$G_A^{-1}\circ f^q\circ G_A$
is also a
![]() $C^0$
-integrable
$C^0$
-integrable
![]() $C^k$
symplectic twist diffeomorphism and
$C^k$
symplectic twist diffeomorphism and
![]() $\mathbb {T}\times \{ 0\}$
is filled with fixed points.
$\mathbb {T}\times \{ 0\}$
is filled with fixed points.
We finally have to prove our theorem in this case and we use the notation f instead of
![]() $G_A^{-1}\circ f^q\circ G_A$
. We can assume that
$G_A^{-1}\circ f^q\circ G_A$
. We can assume that
![]() $\rho (A)=0$
instead of
$\rho (A)=0$
instead of
![]() $\rho (A)\in \mathbb {Z}$
.
$\rho (A)\in \mathbb {Z}$
.
If
![]() $\varepsilon>0$
is arbitrarily small, because of the semi-continuity of the two Green bundles
$\varepsilon>0$
is arbitrarily small, because of the semi-continuity of the two Green bundles
![]() $G_-=\mathbb {R}(1, s_-)$
and
$G_-=\mathbb {R}(1, s_-)$
and
![]() $G_+=\mathbb {R}(1, s_+)$
, we have that for any point
$G_+=\mathbb {R}(1, s_+)$
, we have that for any point
![]() $x=(\theta , r)$
sufficiently close to
$x=(\theta , r)$
sufficiently close to
![]() $\mathbb {T}\times \{ 0\}$
:
$\mathbb {T}\times \{ 0\}$
:
![]() $\max \{\lvert s_-(x)\rvert , \lvert s_+(x)\rvert \} <\varepsilon $
is small.
$\max \{\lvert s_-(x)\rvert , \lvert s_+(x)\rvert \} <\varepsilon $
is small.
Now we fix c small and consider for every
![]() $\theta \in \mathbb {T}$
the small triangular domain
$\theta \in \mathbb {T}$
the small triangular domain
![]() ${\mathcal T}(\theta )$
that is delimited by the following three curves:
${\mathcal T}(\theta )$
that is delimited by the following three curves:
-
• the graph of
 $\eta _c$
;
$\eta _c$
; -
• the vertical
 ${\mathcal V}_\theta =\{\theta \}\times \mathbb {R}$
;
${\mathcal V}_\theta =\{\theta \}\times \mathbb {R}$
; -
• the image
 $f({\mathcal V}_\theta )$
of the vertical at
$f({\mathcal V}_\theta )$
of the vertical at
 $\theta $
.
$\theta $
.

To be more precise,
![]() ${\mathcal T}(\theta )$
is ‘semi-open’ in the following sense; it contains its entire boundary except for the image
${\mathcal T}(\theta )$
is ‘semi-open’ in the following sense; it contains its entire boundary except for the image
![]() $f({\mathcal V}_\theta )$
of the vertical at
$f({\mathcal V}_\theta )$
of the vertical at
![]() $\theta $
.
$\theta $
.
We assume that
![]() $c>0$
. The case
$c>0$
. The case
![]() $c<0$
is similar.
$c<0$
is similar.
As the slope of
![]() $\eta _c$
is almost
$\eta _c$
is almost
![]() $0$
(because between the slope of the two Green bundles; see Proposition B.1) and the slope of the side of the triangle that is in
$0$
(because between the slope of the two Green bundles; see Proposition B.1) and the slope of the side of the triangle that is in
![]() $f({\mathcal V}_\theta )$
is almost
$f({\mathcal V}_\theta )$
is almost
![]() ${1}/{s(\theta )}$
where
${1}/{s(\theta )}$
where
![]() $s(\theta )>0$
is the torsion that is defined by
$s(\theta )>0$
is the torsion that is defined by
 $$ \begin{align} Df(\theta, 0)=\begin{pmatrix} 1&s(\theta)\\ 0& 1\end{pmatrix},\end{align} $$
$$ \begin{align} Df(\theta, 0)=\begin{pmatrix} 1&s(\theta)\\ 0& 1\end{pmatrix},\end{align} $$
the area of this triangle is
where
Let
![]() $\lambda $
be the Lebesgue measure restricted to the invariant sub-annulus
$\lambda $
be the Lebesgue measure restricted to the invariant sub-annulus
Being symplectic, f preserves
![]() $\lambda $
. Moreover, every ergodic measure
$\lambda $
. Moreover, every ergodic measure
![]() $\mu $
for f with support in
$\mu $
for f with support in
![]() ${\mathcal A}_c$
is supported on one curve
${\mathcal A}_c$
is supported on one curve
![]() $\Gamma _A$
with
$\Gamma _A$
with
![]() $A\in [0, c]$
. But
$A\in [0, c]$
. But
![]() $f_{\lvert \Gamma _A}$
is semi-conjugate to a rotation with an angle
$f_{\lvert \Gamma _A}$
is semi-conjugate to a rotation with an angle
![]() $\rho (A)$
that is in
$\rho (A)$
that is in
![]() $[0, 1[$
. Hence every interval in
$[0, 1[$
. Hence every interval in
![]() $\Gamma _A$
that is between some
$\Gamma _A$
that is between some
![]() $(\theta , \eta _A(\theta ))$
and
$(\theta , \eta _A(\theta ))$
and
![]() $f(\theta , \eta _A(\theta ))$
has the same
$f(\theta , \eta _A(\theta ))$
has the same
![]() $\mu $
-measure, which is just given by the rotation number
$\mu $
-measure, which is just given by the rotation number
![]() $\rho (A)\in [0, 1]$
on the graph of
$\rho (A)\in [0, 1]$
on the graph of
![]() $\eta _A$
. This implies that
$\eta _A$
. This implies that
![]() $\theta \mapsto \mu ({\mathcal T}(\theta ))$
is constant. Hence for every
$\theta \mapsto \mu ({\mathcal T}(\theta ))$
is constant. Hence for every
![]() $\theta , \theta '\in \mathbb {T}$
and for every ergodic measure
$\theta , \theta '\in \mathbb {T}$
and for every ergodic measure
![]() $\mu $
with support in
$\mu $
with support in
![]() ${\mathcal A}_c$
, we have
${\mathcal A}_c$
, we have
![]() $\mu ({\mathcal T}(\theta ))=\mu ({\mathcal T}(\theta '))$
.
$\mu ({\mathcal T}(\theta ))=\mu ({\mathcal T}(\theta '))$
.
We now use the ergodic decomposition of invariant measures (see, for example, [Reference Mañé14]) applied to the Lebesgue measure restricted to
![]() ${\mathcal A}_c$
. Let
${\mathcal A}_c$
. Let
![]() $\delta _x$
be the notation for the Dirac measure at x. For every
$\delta _x$
be the notation for the Dirac measure at x. For every
![]() $a\in \mathbb {A}$
, we denote
$a\in \mathbb {A}$
, we denote
![]() ${\lim _{n\rightarrow \infty }({1}/{n})\sum _{k=1}^{n-1}\delta _{f^n(a)}}$
by
${\lim _{n\rightarrow \infty }({1}/{n})\sum _{k=1}^{n-1}\delta _{f^n(a)}}$
by
![]() $\lambda _a$
(such a limit exists and is ergodic as all Birkhoff averages converge to an ergodic measure for orientation-preserving circle homeomorphisms). Then we have
$\lambda _a$
(such a limit exists and is ergodic as all Birkhoff averages converge to an ergodic measure for orientation-preserving circle homeomorphisms). Then we have
![]() $\lambda =\int _{{\mathcal A}_c}\!\lambda _a d\lambda (a)$
. Denoting the rotation number of a point
$\lambda =\int _{{\mathcal A}_c}\!\lambda _a d\lambda (a)$
. Denoting the rotation number of a point
![]() $a\in \mathbb {A}$
by
$a\in \mathbb {A}$
by
![]() ${\mathcal R}(a)$
, we deduce that,
${\mathcal R}(a)$
, we deduce that,
 $$ \begin{align}\text{for all } \theta, \theta'\in \mathbb{T},\quad \lambda({\mathcal T}(\theta))=\lambda({\mathcal T}(\theta'))=\int_{{\mathcal A}_c}\!\! {\mathcal R}(a)\, d\lambda(a).\end{align} $$
$$ \begin{align}\text{for all } \theta, \theta'\in \mathbb{T},\quad \lambda({\mathcal T}(\theta))=\lambda({\mathcal T}(\theta'))=\int_{{\mathcal A}_c}\!\! {\mathcal R}(a)\, d\lambda(a).\end{align} $$
This last inequality is again a consequence of the fact that for all
![]() $a\in {\mathcal A}_c$
,
$a\in {\mathcal A}_c$
,
![]() $\lambda _a({\mathcal T}(\theta )) = {\mathcal R}(a)$
as explained above.
$\lambda _a({\mathcal T}(\theta )) = {\mathcal R}(a)$
as explained above.
We deduce from equation (3) that
 $$ \begin{align*}\text{uniformly for }\theta, \theta'\in\mathbb{T},\quad \lim_{c\rightarrow 0} \frac{\eta_c(\theta')}{\eta_c(\theta)}=\sqrt{\frac{s(\theta)}{s(\theta')}}.\end{align*} $$
$$ \begin{align*}\text{uniformly for }\theta, \theta'\in\mathbb{T},\quad \lim_{c\rightarrow 0} \frac{\eta_c(\theta')}{\eta_c(\theta)}=\sqrt{\frac{s(\theta)}{s(\theta')}}.\end{align*} $$
Integrating with respect to
![]() $\theta '$
and recalling that
$\theta '$
and recalling that
![]() $\int _{\mathbb {T}} \eta _c = c$
, we deduce that uniformly in
$\int _{\mathbb {T}} \eta _c = c$
, we deduce that uniformly in
![]() $\theta $
, we have
$\theta $
, we have
This implies that
 $$ \begin{align} \frac{\partial \eta_c(\theta)}{\partial c}_{\lvert c=0} =\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\frac{1}{\sqrt{s(\theta)}}, \end{align} $$
$$ \begin{align} \frac{\partial \eta_c(\theta)}{\partial c}_{\lvert c=0} =\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\frac{1}{\sqrt{s(\theta)}}, \end{align} $$
and even
 $$ \begin{align} \eta_c(\theta)=c\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\bigg(\frac{1}{\sqrt{s(\theta)}}+\varepsilon(\theta,c)\bigg), \end{align} $$
$$ \begin{align} \eta_c(\theta)=c\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\bigg(\frac{1}{\sqrt{s(\theta)}}+\varepsilon(\theta,c)\bigg), \end{align} $$
where
Observe that
![]() $ {\partial \eta _c}/{\partial c}=( \int _{\mathbb {T}} ({dt}/{\sqrt {s(t)}}))^{-1}({1}/{\sqrt {s(\cdot )}})$
is a
$ {\partial \eta _c}/{\partial c}=( \int _{\mathbb {T}} ({dt}/{\sqrt {s(t)}}))^{-1}({1}/{\sqrt {s(\cdot )}})$
is a
![]() $C^{k-1}$
function of
$C^{k-1}$
function of
![]() $\theta $
. This proves the first point of Theorem 2.1.
$\theta $
. This proves the first point of Theorem 2.1.
![]() $\square $
$\square $
Proof of the second point of Theorem 2.1. We deduce from the first point that for any c such that
![]() $\rho (c)$
is rational, the function
$\rho (c)$
is rational, the function
![]() ${\partial \eta _c}/{\partial c} $
is continuous and positive. Moreover, its integral on
${\partial \eta _c}/{\partial c} $
is continuous and positive. Moreover, its integral on
![]() $\mathbb {T}$
is 1. Hence
$\mathbb {T}$
is 1. Hence
![]() ${\partial \eta _c}/{\partial c} $
is the density of a Borel probability measure that is equivalent to Lebesgue. We now introduce some notation.
${\partial \eta _c}/{\partial c} $
is the density of a Borel probability measure that is equivalent to Lebesgue. We now introduce some notation.
Notation. If
![]() $c<c'$
, we denote by
$c<c'$
, we denote by
![]() $\Lambda _{c, c'}$
the normalized Lebesgue measure between the graph of
$\Lambda _{c, c'}$
the normalized Lebesgue measure between the graph of
![]() $\eta _c$
and the graph of
$\eta _c$
and the graph of
![]() $\eta _{c'}$
, that is, the Lebesgue measure divided by the area between the graph of
$\eta _{c'}$
, that is, the Lebesgue measure divided by the area between the graph of
![]() $\eta _c$
and the graph of
$\eta _c$
and the graph of
![]() $\eta _{c'}$
.
$\eta _{c'}$
.
Then f preserves
![]() $\Lambda _{c, c'}$
. Observe that for any measurable
$\Lambda _{c, c'}$
. Observe that for any measurable
![]() $I\subset \mathbb {T}$
, we have
$I\subset \mathbb {T}$
, we have
Lemma 2.1. If
![]() $\rho (c)$
is rational, then
$\rho (c)$
is rational, then
![]() ${\lim _{c'\rightarrow c}\Lambda _{c, c'}}$
is a measure supported on the graph of
${\lim _{c'\rightarrow c}\Lambda _{c, c'}}$
is a measure supported on the graph of
![]() $\eta _c$
whose projected measure
$\eta _c$
whose projected measure
![]() $\mu _c$
has density
$\mu _c$
has density
![]() ${\partial \eta _c}/{\partial c}$
with respect to the Lebesgue measure of
${\partial \eta _c}/{\partial c}$
with respect to the Lebesgue measure of
![]() $\mathbb {T}$
. Hence if
$\mathbb {T}$
. Hence if
![]() $h_c(\theta )=\int _0^\theta ({\partial \eta _c}/{\partial c})(t)\,dt$
, we have
$h_c(\theta )=\int _0^\theta ({\partial \eta _c}/{\partial c})(t)\,dt$
, we have
Proof. Using equation (6), we can take the limit in equation (7), or more precisely for any
![]() $\psi \in C^0(\mathbb {A}, \mathbb {R})$
in
$\psi \in C^0(\mathbb {A}, \mathbb {R})$
in
 $$ \begin{align*}\int \psi(\theta, r)\, d\Lambda_{c, c'}(\theta, r)=\int_{\mathbb{T}}\frac{1}{c-c'}\bigg( {\int_{\eta_{c'}(\theta)}^{\eta_c(\theta)}\psi(\theta, r)\,dr}\bigg)\, d\theta,\end{align*} $$
$$ \begin{align*}\int \psi(\theta, r)\, d\Lambda_{c, c'}(\theta, r)=\int_{\mathbb{T}}\frac{1}{c-c'}\bigg( {\int_{\eta_{c'}(\theta)}^{\eta_c(\theta)}\psi(\theta, r)\,dr}\bigg)\, d\theta,\end{align*} $$
and obtain that the limit is an invariant measure supported in the graph of
![]() $\eta _c$
whose projected measure
$\eta _c$
whose projected measure
![]() $\mu _c$
has a density with respect to Lebesgue (hence has no atoms) that is equal to
$\mu _c$
has a density with respect to Lebesgue (hence has no atoms) that is equal to
![]() ${\partial \eta _c}/{\partial c}$
. Moreover, by [Reference Arnaud1] (this fact was recalled at the beginning of §2.2),
${\partial \eta _c}/{\partial c}$
. Moreover, by [Reference Arnaud1] (this fact was recalled at the beginning of §2.2),
![]() $g_c$
is
$g_c$
is
![]() $C^0$
conjugate to a rotation. We then use Proposition 2.1 to conclude that
$C^0$
conjugate to a rotation. We then use Proposition 2.1 to conclude that
![]() $h_c$
is the desired conjugacy.
$h_c$
is the desired conjugacy.
Proof of the third point of Theorem 2.1. We notice that when
![]() $\rho (c)$
is irrational, there is only one invariant Borel probability measure that is supported on the graph of
$\rho (c)$
is irrational, there is only one invariant Borel probability measure that is supported on the graph of
![]() $\eta _c$
. This implies the continuity of the map
$\eta _c$
. This implies the continuity of the map
![]() $c\mapsto \mu _c$
at such a c. Let us look at what happens when
$c\mapsto \mu _c$
at such a c. Let us look at what happens when
![]() $\rho (c)$
is rational.
$\rho (c)$
is rational.
Proposition 2.3. For every
![]() $c_0\in \mathbb {R}$
such that
$c_0\in \mathbb {R}$
such that
![]() $\rho (c_0)$
is rational, for every
$\rho (c_0)$
is rational, for every
![]() $\theta \in [0, 1]$
, we have
$\theta \in [0, 1]$
, we have
and the limit is uniform in
![]() $\theta $
.
$\theta $
.
Together with the continuity of
![]() $h_{c_0}$
, this implies the continuity of
$h_{c_0}$
, this implies the continuity of
![]() $(\theta , c)\mapsto h_c(\theta )$
at
$(\theta , c)\mapsto h_c(\theta )$
at
![]() $(\theta , c_0)$
.
$(\theta , c_0)$
.
Proof. In this proof, we will use different functions
![]() $\varepsilon _i(\tau , c)$
and, uniformly in
$\varepsilon _i(\tau , c)$
and, uniformly in
![]() $\tau $
, all these functions will satisfy
$\tau $
, all these functions will satisfy
As in the proof of the first point of Theorem 2.1, we can assume that
![]() $\eta _{c_0}=0$
(and then
$\eta _{c_0}=0$
(and then
![]() $c_0=0$
) and
$c_0=0$
) and
![]() $\rho (0)=0$
.
$\rho (0)=0$
.
We fix
![]() $\varepsilon>0$
. Because of the continuity of
$\varepsilon>0$
. Because of the continuity of
![]() $\rho $
, we can choose
$\rho $
, we can choose
![]() $\alpha $
such that if
$\alpha $
such that if
![]() $\lvert c\rvert <\alpha $
, then
$\lvert c\rvert <\alpha $
, then
![]() $\lvert \rho (c)\rvert <\varepsilon $
.
$\lvert \rho (c)\rvert <\varepsilon $
.
Let us introduce the notation
![]() $N_c=\lfloor {1}/{\rho (c)}\rfloor $
for
$N_c=\lfloor {1}/{\rho (c)}\rfloor $
for
![]() $c\not =0$
. Let us assume that
$c\not =0$
. Let us assume that
![]() $c>0$
and
$c>0$
and
![]() $\theta \in (0, 1]$
. We also denote by
$\theta \in (0, 1]$
. We also denote by
![]() $ \tilde g_c : \mathbb {R} \to \mathbb {R}$
the lift of
$ \tilde g_c : \mathbb {R} \to \mathbb {R}$
the lift of
![]() $g_c$
such that
$g_c$
such that
![]() $ \tilde g_c(0)\in [0, 1)$
and by
$ \tilde g_c(0)\in [0, 1)$
and by
![]() $M_c(\theta )$
,
$M_c(\theta )$
,
Hence,
![]() $M_c(\theta )$
is the number of points of the orbit of
$M_c(\theta )$
is the number of points of the orbit of
![]() $0$
under
$0$
under
![]() $\tilde g_c$
that belong to
$\tilde g_c$
that belong to
![]() $[0, \theta ]$
. Observe that
$[0, \theta ]$
. Observe that
![]() $M_c(\theta )$
is non-decreasing with respect to
$M_c(\theta )$
is non-decreasing with respect to
![]() $\theta $
.
$\theta $
.
As
![]() $\eta _c>0$
, any primitive
$\eta _c>0$
, any primitive
![]() ${\mathcal N}_c$
of
${\mathcal N}_c$
of
![]() $\eta _c$
is increasing, hence
$\eta _c$
is increasing, hence
![]() $M_c(\theta )$
is also the number of
$M_c(\theta )$
is also the number of
![]() $\tilde g^k(0)$
such that
$\tilde g^k(0)$
such that
![]() ${\mathcal N}_c(\tilde g^k(0))$
belongs to
${\mathcal N}_c(\tilde g^k(0))$
belongs to
![]() $[{\mathcal N}_c(0), {\mathcal N}_c(\theta )]$
, that is,
$[{\mathcal N}_c(0), {\mathcal N}_c(\theta )]$
, that is,
 $$ \begin{align} M_c(\theta)&=\sharp \bigg\{\displaystyle j\in \mathbb{N};\ \int_0^{\tilde g_{c}^j(0)}\eta_{c}(t)\,dt\leq \int_0^{\theta}\eta_{c}(t)\,dt\bigg\}\nonumber\\ & =\sup\bigg\{\displaystyle j\in \mathbb{N};\ \int_0^{\tilde g_{c}^j(0)}\eta_{c}(t)\,dt\leq \int_0^{\theta}\eta_{c}(t)\,dt\bigg\}. \end{align} $$
$$ \begin{align} M_c(\theta)&=\sharp \bigg\{\displaystyle j\in \mathbb{N};\ \int_0^{\tilde g_{c}^j(0)}\eta_{c}(t)\,dt\leq \int_0^{\theta}\eta_{c}(t)\,dt\bigg\}\nonumber\\ & =\sup\bigg\{\displaystyle j\in \mathbb{N};\ \int_0^{\tilde g_{c}^j(0)}\eta_{c}(t)\,dt\leq \int_0^{\theta}\eta_{c}(t)\,dt\bigg\}. \end{align} $$
Note that
![]() $M_c(1)=N_c$
because
$M_c(1)=N_c$
because
![]() $g_c$
has rotation number
$g_c$
has rotation number
![]() $\rho (c)$
and that we have, for all
$\rho (c)$
and that we have, for all
![]() $\theta \in (0, 1]$
,
$\theta \in (0, 1]$
,
![]() $M_c(\theta )\leq N_c$
as
$M_c(\theta )\leq N_c$
as
![]() $M_c$
is non-decreasing. We also have
$M_c$
is non-decreasing. We also have
 $$ \begin{align*}\mu_c([0, \theta])=\sum_{j=0}^{M_c(\theta)-1}\mu_c([\tilde g_c^j(0), \tilde g_c^{j+1}(0)[)+\mu_c([\tilde g^{M_c(\theta)}(0), \theta])\end{align*} $$
$$ \begin{align*}\mu_c([0, \theta])=\sum_{j=0}^{M_c(\theta)-1}\mu_c([\tilde g_c^j(0), \tilde g_c^{j+1}(0)[)+\mu_c([\tilde g^{M_c(\theta)}(0), \theta])\end{align*} $$
and thus
![]() $\mu _c([0, \theta ])=M_c(\theta )\rho (c) +\Delta \rho (c)$
with
$\mu _c([0, \theta ])=M_c(\theta )\rho (c) +\Delta \rho (c)$
with
![]() $\Delta \in [0, 1]$
because
$\Delta \in [0, 1]$
because
![]() $[\tilde g^{M_c(\theta )}(0), \theta ]\subset [\tilde g^{M_c(\theta )}(0), \tilde g^{M_c(\theta )+1}(0)]$
.
$[\tilde g^{M_c(\theta )}(0), \theta ]\subset [\tilde g^{M_c(\theta )}(0), \tilde g^{M_c(\theta )+1}(0)]$
.
Hence
 $$ \begin{align}\mu_c([0, \theta])\in [ M_c(\theta)\rho(c), M_c(\theta)\rho(c)+\rho(c)]\subset \bigg[ \frac{M_c(\theta)}{N_c+1}, \frac{M_c(\theta)+1}{N_c}\bigg].\end{align} $$
$$ \begin{align}\mu_c([0, \theta])\in [ M_c(\theta)\rho(c), M_c(\theta)\rho(c)+\rho(c)]\subset \bigg[ \frac{M_c(\theta)}{N_c+1}, \frac{M_c(\theta)+1}{N_c}\bigg].\end{align} $$
Hence to estimate the measure
![]() $\mu _c([0, \theta ])$
we need a good estimate of the number of j such that
$\mu _c([0, \theta ])$
we need a good estimate of the number of j such that
![]() $\tilde g_{c}^j(0)$
belongs to
$\tilde g_{c}^j(0)$
belongs to
![]() $[0, \theta ]$
. We have proved in equation (6) that
$[0, \theta ]$
. We have proved in equation (6) that
 $$ \begin{align} \eta_{c}(\tau)=\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\frac{c(1+\varepsilon_0(\tau,c))}{\sqrt{s(\tau)}}. \end{align} $$
$$ \begin{align} \eta_{c}(\tau)=\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^{-1}\frac{c(1+\varepsilon_0(\tau,c))}{\sqrt{s(\tau)}}. \end{align} $$
We deduce from equation (2) that
![]() $\tilde g_{c}(\tau )= \tau +(s(\tau )+\varepsilon _1(\tau , c))\eta _c(\tau )$
where, uniformly in
$\tilde g_{c}(\tau )= \tau +(s(\tau )+\varepsilon _1(\tau , c))\eta _c(\tau )$
where, uniformly in
![]() $\tau $
, we have
$\tau $
, we have
![]() ${\lim _{c\rightarrow 0}\varepsilon _1(\tau , c)=0}$
and then, by equation (10),
${\lim _{c\rightarrow 0}\varepsilon _1(\tau , c)=0}$
and then, by equation (10),
 $$ \begin{align}\int_\tau^{\tilde g_{c}(\tau)}\eta_{c}(t)\,dt=\eta_c(\tau)^2(s(\tau)+\varepsilon_2(\tau, c)) =\frac{c^2(1+\varepsilon_3(\tau, c))}{\big(\!\int_{\mathbb{T}} ({dt}/{\sqrt{s(t)}})\big)^2}. \end{align} $$
$$ \begin{align}\int_\tau^{\tilde g_{c}(\tau)}\eta_{c}(t)\,dt=\eta_c(\tau)^2(s(\tau)+\varepsilon_2(\tau, c)) =\frac{c^2(1+\varepsilon_3(\tau, c))}{\big(\!\int_{\mathbb{T}} ({dt}/{\sqrt{s(t)}})\big)^2}. \end{align} $$
This says that the area that is delimited by the zero section, the graph of
![]() $\eta _{c}$
and the vertical lines between
$\eta _{c}$
and the vertical lines between
![]() ${\mathcal V}_\tau $
and
${\mathcal V}_\tau $
and
![]() ${\mathcal V}_{\tilde g_c(\tau )}$
is almost constant (that is, does not depend much on
${\mathcal V}_{\tilde g_c(\tau )}$
is almost constant (that is, does not depend much on
![]() $\tau $
).
$\tau $
).
We deduce from equation (8) that
 $$ \begin{align*}\int_0^{\tilde g_c^{M_c(\theta)}(0)}\eta_c(t)\,dt\leq\int_0^\theta\eta_c(t)\,dt<\int_0^{\tilde g_c^{M_c(\theta)+1}(0)}\eta_c(t)\,dt.\end{align*} $$
$$ \begin{align*}\int_0^{\tilde g_c^{M_c(\theta)}(0)}\eta_c(t)\,dt\leq\int_0^\theta\eta_c(t)\,dt<\int_0^{\tilde g_c^{M_c(\theta)+1}(0)}\eta_c(t)\,dt.\end{align*} $$
Hence
 $$ \begin{align*}\sum_{j=0}^{M_c(\theta)-1}\int_{\tilde g^j(0)}^{\tilde g^{j+1}(0)}\eta_c(t)\,dt\leq \int_0^\theta\eta_c(t)\,dt\leq \sum_{j=0}^{M_c(\theta)}\int_{\tilde g^j(0)}^{\tilde g^{j+1}(0)}\eta_c(t)\,dt.\end{align*} $$
$$ \begin{align*}\sum_{j=0}^{M_c(\theta)-1}\int_{\tilde g^j(0)}^{\tilde g^{j+1}(0)}\eta_c(t)\,dt\leq \int_0^\theta\eta_c(t)\,dt\leq \sum_{j=0}^{M_c(\theta)}\int_{\tilde g^j(0)}^{\tilde g^{j+1}(0)}\eta_c(t)\,dt.\end{align*} $$
Using equation (11), we deduce that
 $$ \begin{align*}M_c(\theta)\frac{ c^2(1+\varepsilon_4(\theta, c))}{\big(\!\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})\big)^2}\leq\frac{c(1+\varepsilon_5(\theta, c))}{\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})}\int_0^\theta \frac{dt}{\sqrt{ s(t)}} <(M_c(\theta)+1)\frac{ c^2(1+\varepsilon_6(\theta, c))}{\big(\!\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})\big)^2}, \end{align*} $$
$$ \begin{align*}M_c(\theta)\frac{ c^2(1+\varepsilon_4(\theta, c))}{\big(\!\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})\big)^2}\leq\frac{c(1+\varepsilon_5(\theta, c))}{\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})}\int_0^\theta \frac{dt}{\sqrt{ s(t)}} <(M_c(\theta)+1)\frac{ c^2(1+\varepsilon_6(\theta, c))}{\big(\!\int_{\mathbb{T}}({dt}/{\sqrt{s(t)}})\big)^2}, \end{align*} $$
and then
 $$ \begin{align}M_c (\theta) =\bigg\lfloor \frac{1}{c}\bigg(\bigg( {\int_{\mathbb{T}} \frac{du}{\sqrt{s(u)}}}\bigg)\bigg( {\int_0^{\theta}\frac{dt}{\sqrt{s(t)}}\bigg)+\varepsilon_7(\theta, c)}\bigg)\bigg\rfloor.\end{align} $$
$$ \begin{align}M_c (\theta) =\bigg\lfloor \frac{1}{c}\bigg(\bigg( {\int_{\mathbb{T}} \frac{du}{\sqrt{s(u)}}}\bigg)\bigg( {\int_0^{\theta}\frac{dt}{\sqrt{s(t)}}\bigg)+\varepsilon_7(\theta, c)}\bigg)\bigg\rfloor.\end{align} $$
This implies that
 $$ \begin{align}N_c=M_c(1)=\bigg\lfloor \frac{1}{c}\bigg(\bigg({\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^2+\varepsilon_8(1, c)\bigg)\bigg\rfloor,\end{align} $$
$$ \begin{align}N_c=M_c(1)=\bigg\lfloor \frac{1}{c}\bigg(\bigg({\int_{\mathbb{T}} \frac{dt}{\sqrt{s(t)}}}\bigg)^2+\varepsilon_8(1, c)\bigg)\bigg\rfloor,\end{align} $$
and by equations (9), (12) and (13),
 $$ \begin{align}\mu_c([0, \theta])=\frac{M_c(\theta)}{N_c}+\varepsilon_9(\theta, c)= \frac{\int_0^{\theta}({dt}/{\sqrt{s(t)}})}{\int_{\mathbb{T}} ({dt}/{\sqrt{s(t)}})}+\varepsilon_{10}(\theta, c)=\mu_0([0,\theta])+\varepsilon_{11}(\theta, c).\end{align} $$
$$ \begin{align}\mu_c([0, \theta])=\frac{M_c(\theta)}{N_c}+\varepsilon_9(\theta, c)= \frac{\int_0^{\theta}({dt}/{\sqrt{s(t)}})}{\int_{\mathbb{T}} ({dt}/{\sqrt{s(t)}})}+\varepsilon_{10}(\theta, c)=\mu_0([0,\theta])+\varepsilon_{11}(\theta, c).\end{align} $$
As none of the measures
![]() $\mu _c$
has atoms, this implies that
$\mu _c$
has atoms, this implies that
![]() $c\mapsto \mu _c$
and all the maps
$c\mapsto \mu _c$
and all the maps
![]() $c\mapsto \mu _c([0, \theta ])=h_c(\theta )$
are continuous. As every map
$c\mapsto \mu _c([0, \theta ])=h_c(\theta )$
are continuous. As every map
![]() $h_c$
is non-decreasing in the variable
$h_c$
is non-decreasing in the variable
![]() $\theta $
, we deduce from the Dini–Polyá theorem [Reference Rudin19, Exercise 13.b, p. 167] that
$\theta $
, we deduce from the Dini–Polyá theorem [Reference Rudin19, Exercise 13.b, p. 167] that
![]() $c\mapsto h_c$
is continuous for the
$c\mapsto h_c$
is continuous for the
![]() $C^0$
uniform topology.
$C^0$
uniform topology.
Remark. If
![]() $\rho (A)={p}/{q}$
, then we proved that
$\rho (A)={p}/{q}$
, then we proved that
 $$ \begin{align*}({\partial \eta_c(\theta)}/{\partial c})_{\vert c=A}\! =\! \bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1} \bigg(\frac{1}{\sqrt{s_q(\theta, \eta_A(\theta))}}\bigg),\end{align*} $$
$$ \begin{align*}({\partial \eta_c(\theta)}/{\partial c})_{\vert c=A}\! =\! \bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1} \bigg(\frac{1}{\sqrt{s_q(\theta, \eta_A(\theta))}}\bigg),\end{align*} $$
where
 $$ \begin{align*}Df^q(x)=\begin{pmatrix} a_q(x)&s_q(x)\\ c_q(x)&d_q(x) \end{pmatrix}.\end{align*} $$
$$ \begin{align*}Df^q(x)=\begin{pmatrix} a_q(x)&s_q(x)\\ c_q(x)&d_q(x) \end{pmatrix}.\end{align*} $$
Indeed, the term
![]() $s_q(t, \eta _c(t))$
does not change when we conjugate by the map
$s_q(t, \eta _c(t))$
does not change when we conjugate by the map
![]() $G_A$
where
$G_A$
where
![]() $G_A(\theta , r)=(\theta , r+\eta _A(\theta ))$
as we did in §2.2.
$G_A(\theta , r)=(\theta , r+\eta _A(\theta ))$
as we did in §2.2.
This gives for the conjugacy
 $$ \begin{align*}h_A(\theta)=\mu_A([0, \theta])=\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1}\int_0^\theta \frac{1}{\sqrt{s_q(t, \eta_A(t))}}\,dt.\end{align*} $$
$$ \begin{align*}h_A(\theta)=\mu_A([0, \theta])=\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1}\int_0^\theta \frac{1}{\sqrt{s_q(t, \eta_A(t))}}\,dt.\end{align*} $$
Observe that this
![]() $C^k$
depends on
$C^k$
depends on
![]() $\theta $
.
$\theta $
.
Observe too that equation (6) can be rewritten as
 $$ \begin{align}\eta_c(\theta)=\eta_A(\theta)+(c-A)\bigg[\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1}\frac{1}{\sqrt{s_q(\theta, \eta_A(\theta))}}+\varepsilon(\theta,c)\bigg], \end{align} $$
$$ \begin{align}\eta_c(\theta)=\eta_A(\theta)+(c-A)\bigg[\bigg( {\int_{\mathbb{T}} \frac{dt}{\sqrt{s_q(t, \eta_A(t))}}}\bigg)^{-1}\frac{1}{\sqrt{s_q(\theta, \eta_A(\theta))}}+\varepsilon(\theta,c)\bigg], \end{align} $$
where
Observe that the formula does not give any continuous dependence of
![]() $h_c$
or
$h_c$
or
![]() ${\partial \eta _c}/{\partial c}$
in the c variable, because q can become very large when c changes.
${\partial \eta _c}/{\partial c}$
in the c variable, because q can become very large when c changes.
2.3 Generating function and regularity
To finish the proof of Theorem 1.1, we have to prove that u admits a derivative with respect to c everywhere and that
Because we proved that
![]() $(\theta , c)\mapsto h_c(\theta )$
is continuous, we will deduce that u is
$(\theta , c)\mapsto h_c(\theta )$
is continuous, we will deduce that u is
![]() $C^1$
.
$C^1$
.
Observe that for every
![]() $\theta $
, the map
$\theta $
, the map
![]() $c\mapsto u(\theta , c)+c\theta $
is increasing because every
$c\mapsto u(\theta , c)+c\theta $
is increasing because every
![]() $ c\mapsto \eta _c(\theta )$
is increasing.
$ c\mapsto \eta _c(\theta )$
is increasing.
Let us restate Theorem 1.1 with the new notation.
Theorem 2.2. The map u is
![]() $C^1$
. Moreover, in this case, we have the following statements.
$C^1$
. Moreover, in this case, we have the following statements.
-
• The graph of
 $c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of the invariant foliation.
$c+({\partial u}/{\partial \theta })(\cdot , c)$
is a leaf of the invariant foliation. -
•
 $ \theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
is the semi-conjugacy
$ \theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
is the semi-conjugacy
 $h_c$
between
$h_c$
between
 $g_c$
and
$g_c$
and
 $R_{\rho (c)}$
given in Theorem 2.1. We have
$R_{\rho (c)}$
given in Theorem 2.1. We have
 $h_c\circ g_c=h_c+\rho (c)$
.
$h_c\circ g_c=h_c+\rho (c)$
.
Proof. The first point is a consequence of the definition of u.
Then
![]() $u(\cdot ,c)$
and
$u(\cdot ,c)$
and
![]() ${\partial u}/{\partial \theta }=\eta _{c}-c$
continuously depend on
${\partial u}/{\partial \theta }=\eta _{c}-c$
continuously depend on
![]() $(\theta , c)$
.
$(\theta , c)$
.
Observe that with the notation (7), we have
 $$ \begin{align*} &\Lambda_{c, c'} (\{ (\theta, r); \ \theta \in [\theta_1, \theta_2], r\in [\eta_{c}(\theta), \eta_{c'}(\theta)]\}) \\ &\quad=\frac{1}{c'-c}( (u(\theta_2, c')-u(\theta_1, c'))-(u(\theta_2,c)-u(\theta_1,c)) )+(\theta_2-\theta_1). \end{align*} $$
$$ \begin{align*} &\Lambda_{c, c'} (\{ (\theta, r); \ \theta \in [\theta_1, \theta_2], r\in [\eta_{c}(\theta), \eta_{c'}(\theta)]\}) \\ &\quad=\frac{1}{c'-c}( (u(\theta_2, c')-u(\theta_1, c'))-(u(\theta_2,c)-u(\theta_1,c)) )+(\theta_2-\theta_1). \end{align*} $$
Moreover, if
![]() $\rho (c_0)\in \mathbb {Q}$
, we deduce from Lemma 2.1 that
$\rho (c_0)\in \mathbb {Q}$
, we deduce from Lemma 2.1 that
![]() $u(\cdot , c)$
admits a derivative with respect to c at
$u(\cdot , c)$
admits a derivative with respect to c at
![]() $c_0$
,
$c_0$
,
that is given by
and this derivative continuously depends on
![]() $\theta $
.
$\theta $
.
Assume now that
![]() $\rho (c_0)$
is irrational and let c tend to
$\rho (c_0)$
is irrational and let c tend to
![]() $c_0$
. Every limit point of
$c_0$
. Every limit point of
![]() $\Lambda _{c, c_0}$
when c tends to
$\Lambda _{c, c_0}$
when c tends to
![]() $c_0$
is a Borel probability measure that is invariant by f and supported on the graph of
$c_0$
is a Borel probability measure that is invariant by f and supported on the graph of
![]() $\eta _{ c_0}$
. As there exists only one such measure, whose projection was denoted by
$\eta _{ c_0}$
. As there exists only one such measure, whose projection was denoted by
![]() $\mu _{c_0}$
, we deduce that
$\mu _{c_0}$
, we deduce that
As
![]() $\mu _{c_0}$
has no atom, we have, for all
$\mu _{c_0}$
has no atom, we have, for all
![]() $\theta _0\in [0, 1)$
,
$\theta _0\in [0, 1)$
,
 $$ \begin{align*} h_{c_0}(\theta_0)&=\ \mu_{c_0}([0, \theta_0]) =\lim_{c\rightarrow c_0}\Lambda_{c_0, c} (\{ (\theta, r); \theta \in [0, \theta_0], r\in [\eta_{c_0}(\theta), \eta_{c}(\theta)]\}) \\ & =\lim_{c\rightarrow c_0}\frac{1}{c-c_0}((u(\theta_0,c)-u(0,c))-(u(\theta_0, c_0)-u(0,c_0)))+\theta_0 \\ &=\frac{\partial u}{\partial c}(\theta_0,c_0)+\theta_{0}. \end{align*} $$
$$ \begin{align*} h_{c_0}(\theta_0)&=\ \mu_{c_0}([0, \theta_0]) =\lim_{c\rightarrow c_0}\Lambda_{c_0, c} (\{ (\theta, r); \theta \in [0, \theta_0], r\in [\eta_{c_0}(\theta), \eta_{c}(\theta)]\}) \\ & =\lim_{c\rightarrow c_0}\frac{1}{c-c_0}((u(\theta_0,c)-u(0,c))-(u(\theta_0, c_0)-u(0,c_0)))+\theta_0 \\ &=\frac{\partial u}{\partial c}(\theta_0,c_0)+\theta_{0}. \end{align*} $$
Let us explain the above equality. If
![]() $\varepsilon>0$
, as
$\varepsilon>0$
, as
![]() $\mu _{c_0}$
has no atoms, there exist two continuous functions
$\mu _{c_0}$
has no atoms, there exist two continuous functions
![]() $\chi ^\pm $
such that
$\chi ^\pm $
such that
![]() $\chi ^-\leq \chi _{[0,\theta ]}\leq \chi ^+$
and
$\chi ^-\leq \chi _{[0,\theta ]}\leq \chi ^+$
and
![]() $\int _{\mathbb {T}} (\chi ^+-\chi ^-)\,d \mu _{c_0} <\varepsilon $
. Setting
$\int _{\mathbb {T}} (\chi ^+-\chi ^-)\,d \mu _{c_0} <\varepsilon $
. Setting
![]() $\nu _c = { \pi _{1*}}(\Lambda _{c, c_0})$
, we have
$\nu _c = { \pi _{1*}}(\Lambda _{c, c_0})$
, we have
![]() $\int _{\mathbb {T}} \chi ^- \,d\nu _c \leq \nu _c([0,\theta ]) \leq \int _{\mathbb {T}} \chi ^+ \,d\nu _c $
. As
$\int _{\mathbb {T}} \chi ^- \,d\nu _c \leq \nu _c([0,\theta ]) \leq \int _{\mathbb {T}} \chi ^+ \,d\nu _c $
. As
![]() $\int _{\mathbb {T}} \chi ^\pm \, d\nu _c \to \int _{\mathbb {T}} \chi ^\pm \, d\mu _{c_0}$
when
$\int _{\mathbb {T}} \chi ^\pm \, d\nu _c \to \int _{\mathbb {T}} \chi ^\pm \, d\mu _{c_0}$
when
![]() $c\to c_0$
, we conclude that
$c\to c_0$
, we conclude that
![]() $\lvert \nu _c([0,\theta ]) - \mu _{c_0}([0,\theta ])\rvert <2\varepsilon $
for c close to
$\lvert \nu _c([0,\theta ]) - \mu _{c_0}([0,\theta ])\rvert <2\varepsilon $
for c close to
![]() $c_0$
.
$c_0$
.
Hence u admits a derivative with respect to c and
Because of Theorem 2.1,
![]() $(\theta , c)\mapsto ({\partial u}/{\partial c})(\theta ,c)=h_c(\theta )-\theta $
is continuous. As the two partial derivatives
$(\theta , c)\mapsto ({\partial u}/{\partial c})(\theta ,c)=h_c(\theta )-\theta $
is continuous. As the two partial derivatives
![]() ${\partial u}/{\partial \theta }$
and
${\partial u}/{\partial \theta }$
and
![]() ${\partial u}/{\partial c}$
are continuous in
${\partial u}/{\partial c}$
are continuous in
![]() $(\theta , c)$
, we conclude that u is
$(\theta , c)$
, we conclude that u is
![]() $C^1$
. This finishes the proof of Theorem 1.1.
$C^1$
. This finishes the proof of Theorem 1.1.
3 Proof of Theorem 1.2
We assume that
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
is a
$f:\mathbb {A}\rightarrow \mathbb {A}$
is a
![]() $C^0$
integrable symplectic twist diffeomorphism with generating function u for its invariant foliation and use the notation
$C^0$
integrable symplectic twist diffeomorphism with generating function u for its invariant foliation and use the notation
![]() ${\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)}$
. We also denote the projected dynamics on the graph of
${\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)}$
. We also denote the projected dynamics on the graph of
![]() $\eta _c$
by
$\eta _c$
by
![]() $\tilde g_c(\theta )=\pi _1\circ F(\theta , \eta _c(\theta ))$
where we fix a lift
$\tilde g_c(\theta )=\pi _1\circ F(\theta , \eta _c(\theta ))$
where we fix a lift
![]() $F:\mathbb {R}^2\rightarrow \mathbb {R}^2$
of f. We work on the compact set
$F:\mathbb {R}^2\rightarrow \mathbb {R}^2$
of f. We work on the compact set
Replacing F by
![]() $F+(0, p)$
for some integer
$F+(0, p)$
for some integer
![]() $p\in \mathbb {N}$
, we can assume that the rotation number
$p\in \mathbb {N}$
, we can assume that the rotation number
![]() ${\mathcal R}(x)$
of every
${\mathcal R}(x)$
of every
![]() $x\in K$
is positive. We denote
$x\in K$
is positive. We denote
![]() $U=\{ (\theta , \eta _c(\theta )); \theta \in \mathbb {T}, c\in (c_1, c_2)\}.$
Being
$U=\{ (\theta , \eta _c(\theta )); \theta \in \mathbb {T}, c\in (c_1, c_2)\}.$
Being
![]() $C^1$
, u is C-Lipschitz on K for some constant
$C^1$
, u is C-Lipschitz on K for some constant
![]() $C>0$
. Using the notation of Appendix B, we recall that
$C>0$
. Using the notation of Appendix B, we recall that
and that all the maps
![]() $s_k$
are continuous. Hence there exist
$s_k$
are continuous. Hence there exist
![]() $b>a>0$
and
$b>a>0$
and
![]() $r\in (0, 1)$
such that
$r\in (0, 1)$
such that
We deduce that,
Working in
![]() $\mathbb {R}^2$
, we consider for any
$\mathbb {R}^2$
, we consider for any
![]() $c,c'\in (c_1, c_2)$
such that
$c,c'\in (c_1, c_2)$
such that
![]() $c<c'$
the domain
$c<c'$
the domain
![]() $D(\theta )$
whose boundary is the union of:
$D(\theta )$
whose boundary is the union of:
-
• the small piece V of the vertical
 $\{\theta \}\times \mathbb {R}$
that is between
$\{\theta \}\times \mathbb {R}$
that is between
 $\eta _c$
and
$\eta _c$
and
 $\eta _{c'}$
;
$\eta _{c'}$
; -
• the arc
 $F(V)$
; and
$F(V)$
; and -
• pieces of
 $\eta _c$
and
$\eta _c$
and
 $\eta _{c'}$
that are between V and
$\eta _{c'}$
that are between V and
 $F(V)$
.
$F(V)$
.

Using the same method as in §2.2 for the rational curve case (that is, the decomposition of Lebesgue measure into ergodic measures), we see that the area of
![]() $D(\theta )$
does not depend on
$D(\theta )$
does not depend on
![]() $\theta $
.
$\theta $
.
We then cut
![]() $D(\theta )$
into three subsets.
$D(\theta )$
into three subsets.
-
• If
 $p=\lfloor \tilde g_c(\theta )-\theta \rfloor $
,
$p=\lfloor \tilde g_c(\theta )-\theta \rfloor $
,
 $D_1(\theta )$
is the domain that is between V,
$D_1(\theta )$
is the domain that is between V,
 $V+p$
and the graphs of
$V+p$
and the graphs of
 $\eta _c$
and
$\eta _c$
and
 $\eta _{c'}$
. Observe that
$\eta _{c'}$
. Observe that
 $p=\lfloor {\mathcal R} (\theta , \eta _c(\theta ))\rfloor =\lfloor \rho (c)\rfloor $
does not depend on
$p=\lfloor {\mathcal R} (\theta , \eta _c(\theta ))\rfloor =\lfloor \rho (c)\rfloor $
does not depend on
 $\theta $
(recall that when restricted to the graph of
$\theta $
(recall that when restricted to the graph of
 $\eta _c$
, either f is periodic and all points have the same period, or f has no periodic orbit).
$\eta _c$
, either f is periodic and all points have the same period, or f has no periodic orbit). -
•
 $D_2(\theta )$
is the domain between
$D_2(\theta )$
is the domain between
 $V+p$
, the vertical
$V+p$
, the vertical
 $V^*$
at
$V^*$
at
 $F(\theta , \eta _c(\theta ))$
and the graphs of
$F(\theta , \eta _c(\theta ))$
and the graphs of
 $\eta _c$
and
$\eta _c$
and
 $\eta _{c'}$
.
$\eta _{c'}$
. -
•
 $D_3(\theta )$
is the triangular domain between
$D_3(\theta )$
is the triangular domain between
 $V^*$
,
$V^*$
,
 $F(V)$
and
$F(V)$
and
 $\eta _{c'}$
.
$\eta _{c'}$
.

Then the area of
![]() $D_1(\theta )$
is
$D_1(\theta )$
is
![]() $p(c'-c)$
and does not depend on
$p(c'-c)$
and does not depend on
![]() $\theta $
.
$\theta $
.
The area of
![]() $D_2(\theta )$
is
$D_2(\theta )$
is
 $$ \begin{align*}\int_{\theta+p}^{ \tilde g_c(\theta)}\bigg( \bigg(c'+\frac{\partial u}{\partial \theta}(t, c')\bigg)-\bigg(c+\frac{\partial u}{\partial \theta}(t, c)\bigg)\bigg)\, dt,\end{align*} $$
$$ \begin{align*}\int_{\theta+p}^{ \tilde g_c(\theta)}\bigg( \bigg(c'+\frac{\partial u}{\partial \theta}(t, c')\bigg)-\bigg(c+\frac{\partial u}{\partial \theta}(t, c)\bigg)\bigg)\, dt,\end{align*} $$
a positive number equal to
We recall that u is C Lipschitz on K and that
![]() $ \tilde g_c(\theta )-\theta -p\in (0, 1)$
. We deduce that the area of
$ \tilde g_c(\theta )-\theta -p\in (0, 1)$
. We deduce that the area of
![]() $D_2(\theta )$
belongs to
$D_2(\theta )$
belongs to
We want now to estimate the area of the triangle
![]() $D_3(\theta )$
. This triangle has three (curved) sides:
$D_3(\theta )$
. This triangle has three (curved) sides:
-
• the vertical side
 $V^*$
whose length is equal to
$V^*$
whose length is equal to
 $\eta _{c'}( \tilde g_c(\theta ))-\eta _{c}( \tilde g_c(\theta ))$
;
$\eta _{c'}( \tilde g_c(\theta ))-\eta _{c}( \tilde g_c(\theta ))$
; -
• the side
 $F(V)$
with slope at
$F(V)$
with slope at
 $x\in F(V)$
equal to
$x\in F(V)$
equal to
 $s_1(x)$
;
$s_1(x)$
; -
• the side H supported in
 $\eta _{c'}$
that is Lipschitz with tangent cone at x that is contained in
$\eta _{c'}$
that is Lipschitz with tangent cone at x that is contained in
 $[s_-(x), s_+(x)]\subset [s_{-1}(x), s_2(x)]$
.
$[s_-(x), s_+(x)]\subset [s_{-1}(x), s_2(x)]$
.
Because of the continuity of the foliation, there exists
![]() $\nu>0$
such that if
$\nu>0$
such that if
![]() $c_1\leq c\leq c'\leq c_2$
and
$c_1\leq c\leq c'\leq c_2$
and
![]() $c'-c<\nu $
, then the length of every piece of vertical V between
$c'-c<\nu $
, then the length of every piece of vertical V between
![]() $\eta _c$
and
$\eta _c$
and
![]() $\eta _{c'}$
is less than r (recall that r was chosen to satisfy Formula (17)) and the same is true for
$\eta _{c'}$
is less than r (recall that r was chosen to satisfy Formula (17)) and the same is true for
![]() $F(V)$
because of the uniform continuity of F on the strip between
$F(V)$
because of the uniform continuity of F on the strip between
![]() $\eta _{c_1}$
and
$\eta _{c_1}$
and
![]() $\eta _{c_2}$
. Without loss of generality, we assume furthermore that
$\eta _{c_2}$
. Without loss of generality, we assume furthermore that
![]() $\nu <1$
. Using the fact that the tangent cone to the graph of
$\nu <1$
. Using the fact that the tangent cone to the graph of
![]() $\eta _{c'}$
is between the two Green bundles (see Appendix B) and equation (16), we deduce that if
$\eta _{c'}$
is between the two Green bundles (see Appendix B) and equation (16), we deduce that if
![]() $c'-c\in [0, \nu )$
, then
$c'-c\in [0, \nu )$
, then
![]() $D_3(\theta )$
$D_3(\theta )$
-
• is contained in a true triangle with vertical side equal to
 $V^*$
, upper side with slope equal to
$V^*$
, upper side with slope equal to
 ${\max _{x\in H}s_2(x)}$
and slope of lower side equal to
${\max _{x\in H}s_2(x)}$
and slope of lower side equal to
 ${\min _{x\in F(V)}s_1(x)}$
, and
${\min _{x\in F(V)}s_1(x)}$
, and -
• contains a true triangle with vertical side equal to
 $V^*$
, upper side with slope equal to
$V^*$
, upper side with slope equal to
 ${\min _{x\in H}s_{-1}(x)}$
and slope of lower side equal to
${\min _{x\in H}s_{-1}(x)}$
and slope of lower side equal to
 ${\max _{x\in F(V)}s_1(x)};$
${\max _{x\in F(V)}s_1(x)};$
Observe that when the triangle is a true triangle, its horizontal height has length
![]() ${\delta }/{S-T}$
where
${\delta }/{S-T}$
where
![]() $\delta $
is the length of the vertical side, T is the slope of the side coming from the upper point of the vertical side and S is the slope of the side coming from the lower point of the vertical side. The area is then
$\delta $
is the length of the vertical side, T is the slope of the side coming from the upper point of the vertical side and S is the slope of the side coming from the lower point of the vertical side. The area is then
![]() ${\delta ^2}/{2(S-T)}$
${\delta ^2}/{2(S-T)}$
These remarks and equation (17) imply that the area of
![]() $D_3(\theta )$
belongs to the interval
$D_3(\theta )$
belongs to the interval
 $$ \begin{align*}\bigg[\frac{(\eta_{c'} (\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2b},\frac{(\eta_{c'}(\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2a}\bigg].\end{align*} $$
$$ \begin{align*}\bigg[\frac{(\eta_{c'} (\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2b},\frac{(\eta_{c'}(\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2a}\bigg].\end{align*} $$
Finally, the sum
![]() $A(\theta )$
of the area of
$A(\theta )$
of the area of
![]() $D_2(\theta )$
and
$D_2(\theta )$
and
![]() $D_3(\theta )$
does not depend on
$D_3(\theta )$
does not depend on
![]() $\theta $
and, recalling we are assuming
$\theta $
and, recalling we are assuming
![]() $c'-c<\nu <1$
:
$c'-c<\nu <1$
:
-
• at a point (which always exists because
 $\int _{\mathbb {T}}(\eta _c-\eta _{c'})=c-c'$
) such that
$\int _{\mathbb {T}}(\eta _c-\eta _{c'})=c-c'$
) such that
 $\eta _{c'}(\tilde g_c(\theta ))-\eta _c(\tilde g_c(\theta ))=c'-c$
, we have
$\eta _{c'}(\tilde g_c(\theta ))-\eta _c(\tilde g_c(\theta ))=c'-c$
, we have  $$ \begin{align*}A(\theta)&\in\bigg[ \frac{(c'-c)^2}{2b},\frac{(c'-c)^2}{2a}+ (2C+1)(c'-c) \bigg]\\[3pt] &\subset \bigg[ \frac{(c'-c)^2}{2b}, \bigg( (2C+1)+\frac{1}{2a}\bigg)(c'-c)\bigg]; \end{align*} $$
$$ \begin{align*}A(\theta)&\in\bigg[ \frac{(c'-c)^2}{2b},\frac{(c'-c)^2}{2a}+ (2C+1)(c'-c) \bigg]\\[3pt] &\subset \bigg[ \frac{(c'-c)^2}{2b}, \bigg( (2C+1)+\frac{1}{2a}\bigg)(c'-c)\bigg]; \end{align*} $$
-
• at every point, we have
 $$ \begin{align*}A(\theta)\geq \textrm{area}(D_3(\theta))\geq \frac{(\eta_{c'}(\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2b};\end{align*} $$
$$ \begin{align*}A(\theta)\geq \textrm{area}(D_3(\theta))\geq \frac{(\eta_{c'}(\tilde g_c(\theta))-\eta_{c}(\tilde g_c(\theta)))^2}{2b};\end{align*} $$
This implies that for
![]() $c_1\leq c\leq c'\leq c_2$
such that
$c_1\leq c\leq c'\leq c_2$
such that
![]() $c'-c<\nu $
, we have
$c'-c<\nu $
, we have
 $$ \begin{align*}\text{for all } \theta \in \mathbb{R}, \quad \frac{(\eta_{c'}(\theta)-\eta_{c}(\theta))^2}{2b}\leq \bigg( (2C+1)+\frac{1}{2a}\bigg)(c'-c),\end{align*} $$
$$ \begin{align*}\text{for all } \theta \in \mathbb{R}, \quad \frac{(\eta_{c'}(\theta)-\eta_{c}(\theta))^2}{2b}\leq \bigg( (2C+1)+\frac{1}{2a}\bigg)(c'-c),\end{align*} $$
so
 $$ \begin{align*}\text{for all } \theta \in \mathbb{R},\quad \eta_{c'}(\theta)-\eta_{c}(\theta)\leq \sqrt{2b \bigg((2C+1)+\frac{1}{2a}\bigg)(c'-c)}.\end{align*} $$
$$ \begin{align*}\text{for all } \theta \in \mathbb{R},\quad \eta_{c'}(\theta)-\eta_{c}(\theta)\leq \sqrt{2b \bigg((2C+1)+\frac{1}{2a}\bigg)(c'-c)}.\end{align*} $$
Hence we obtain on the compact K a uniform local constant of Hölder, and this implies that
![]() $\eta _c$
is uniformly
$\eta _c$
is uniformly
![]() $\tfrac 12$
-Hölder in the variable c on K.
$\tfrac 12$
-Hölder in the variable c on K.
4 Proof of Theorem 1.3
We recall that
![]() ${\mathcal U}$
,
${\mathcal U}$
,
![]() ${\mathcal V}$
are open subsets of either
${\mathcal V}$
are open subsets of either
![]() $\mathbb {A}$
or
$\mathbb {A}$
or
![]() $\mathbb {R}^2$
and that:
$\mathbb {R}^2$
and that:
-
•
 ${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and }a(\theta )<r<b(\theta )\}$
or
${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and }a(\theta )<r<b(\theta )\}$
or
 ${\mathcal V}=\mathbb {A}$
where
${\mathcal V}=\mathbb {A}$
where
 $a, b$
are continuous functions defined on
$a, b$
are continuous functions defined on
 $[\alpha , \beta ]$
and that
$[\alpha , \beta ]$
and that
 $0\in (\alpha , \beta )$
;
$0\in (\alpha , \beta )$
; -
•
 ${\mathcal U}=\{(x,c); c\in (c_-, c_+)\text { and }d(c)< x< e(c)\}$
or
${\mathcal U}=\{(x,c); c\in (c_-, c_+)\text { and }d(c)< x< e(c)\}$
or
 ${\mathcal U}=\mathbb {A}$
where
${\mathcal U}=\mathbb {A}$
where
 $d, e$
are continuous functions defined on
$d, e$
are continuous functions defined on
 $[c_-, c_+]$
.
$[c_-, c_+]$
.
With this notation,
![]() $\partial ^+{\mathcal U}=[d(c_+), e(c_+)]\times \{ c_+\}$
(respectively,
$\partial ^+{\mathcal U}=[d(c_+), e(c_+)]\times \{ c_+\}$
(respectively,
![]() $\partial ^-{\mathcal U}=[d(c_-), e(c_-)]\times \{ c_-\}$
) is the upper (respectively, lower) boundary of
$\partial ^-{\mathcal U}=[d(c_-), e(c_-)]\times \{ c_-\}$
) is the upper (respectively, lower) boundary of
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() $\partial ^+{\mathcal V}=\{ (t, b(t)); t\in [\alpha , \beta ]\}$
(respectively,
$\partial ^+{\mathcal V}=\{ (t, b(t)); t\in [\alpha , \beta ]\}$
(respectively,
![]() $\partial ^-{\mathcal V}=\{ (t, a(t)); t\in [\alpha , \beta ]\}$
) is the upper (respectively, lower) boundary of
$\partial ^-{\mathcal V}=\{ (t, a(t)); t\in [\alpha , \beta ]\}$
) is the upper (respectively, lower) boundary of
![]() ${\mathcal V}$
.
${\mathcal V}$
.
We use the notation
Then
![]() ${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
or
${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
or
![]() ${\mathcal W}=\mathbb {A}$
.
${\mathcal W}=\mathbb {A}$
.
Let us consider a
![]() $C^0$
-foliation
$C^0$
-foliation
![]() ${\mathcal F}$
of
${\mathcal F}$
of
![]() ${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and }\eta _{c_-}(\theta )<r<\eta _{c_+}(\theta )\}$
or
${\mathcal V}=\{ (\theta , r); \theta \in (\alpha , \beta )\text { and }\eta _{c_-}(\theta )<r<\eta _{c_+}(\theta )\}$
or
![]() ${\mathcal V}=\mathbb {A}$
into graphs:
${\mathcal V}=\mathbb {A}$
into graphs:
![]() $(\theta , c)\in {\mathcal W} \mapsto (\theta , \eta _c(\theta ))$
(when
$(\theta , c)\in {\mathcal W} \mapsto (\theta , \eta _c(\theta ))$
(when
![]() ${\mathcal V}=\mathbb {A}$
,
${\mathcal V}=\mathbb {A}$
,
![]() ${\mathcal W}=\mathbb {A}$
and in the other cases
${\mathcal W}=\mathbb {A}$
and in the other cases
![]() ${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
). When
${\mathcal W}=(\alpha , \beta )\times (c_-, c_+)$
). When
![]() ${\mathcal V}=\mathbb {A}$
we insist that
${\mathcal V}=\mathbb {A}$
we insist that
![]() $\int _{\mathbb {T}} \eta _c = c$
for all
$\int _{\mathbb {T}} \eta _c = c$
for all
![]() $c\in \mathbb {R}$
. Then there exists a continuous function
$c\in \mathbb {R}$
. Then there exists a continuous function
![]() $u:{\mathcal W}\rightarrow \mathbb {R}$
that admits a continuous derivative with respect to
$u:{\mathcal W}\rightarrow \mathbb {R}$
that admits a continuous derivative with respect to
![]() $\theta $
such that
$\theta $
such that
![]() $\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta ,c)$
and
$\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta ,c)$
and
![]() $u(0, c)=0$
, a function that we called generating function of the foliation when
$u(0, c)=0$
, a function that we called generating function of the foliation when
![]() ${\mathcal V}=\mathbb {A}$
.
${\mathcal V}=\mathbb {A}$
.
4.1 Proof of the first implication
Let
![]() $\Phi :{\mathcal U}\rightarrow {\mathcal V}$
be an exact symplectic homeomorphism that maps the standard horizontal foliation onto a foliation
$\Phi :{\mathcal U}\rightarrow {\mathcal V}$
be an exact symplectic homeomorphism that maps the standard horizontal foliation onto a foliation
![]() ${\mathcal F}$
that is transverse to the vertical one and that preserves the orientation of the leaves. (When
${\mathcal F}$
that is transverse to the vertical one and that preserves the orientation of the leaves. (When
![]() ${\mathcal V}=\mathbb {A}$
, the exactness condition implies that
${\mathcal V}=\mathbb {A}$
, the exactness condition implies that
![]() $\Phi $
maps the circle
$\Phi $
maps the circle
![]() $\mathbb {T}\times \{c\}$
to the graph of
$\mathbb {T}\times \{c\}$
to the graph of
![]() $\eta _c$
. In the other cases, as the domains are simply connected, the exactness condition is empty.) Assume that
$\eta _c$
. In the other cases, as the domains are simply connected, the exactness condition is empty.) Assume that
![]() $\Phi $
extends to a homeomorphism
$\Phi $
extends to a homeomorphism
![]() $\overline {\Phi } : \overline {{\mathcal U}}\to \overline {{\mathcal V}}$
and that
$\overline {\Phi } : \overline {{\mathcal U}}\to \overline {{\mathcal V}}$
and that
![]() $\overline {\Phi }(\partial ^\pm {\mathcal U})=\partial ^\pm {\mathcal V}$
. Then the endpoints of the leaves of
$\overline {\Phi }(\partial ^\pm {\mathcal U})=\partial ^\pm {\mathcal V}$
. Then the endpoints of the leaves of
![]() ${\mathcal F}$
are not in
${\mathcal F}$
are not in
![]() $\partial ^\pm {\mathcal V}$
. As the foliation
$\partial ^\pm {\mathcal V}$
. As the foliation
![]() ${\mathcal F}$
is transverse to the ‘vertical’ foliation
${\mathcal F}$
is transverse to the ‘vertical’ foliation
![]() ${\mathcal G}_0$
into
${\mathcal G}_0$
into
![]() $\pi _1^{-1}(\{\theta \})$
for
$\pi _1^{-1}(\{\theta \})$
for
![]() $\theta \in \pi _1({\mathcal V})$
, all the leaves of
$\theta \in \pi _1({\mathcal V})$
, all the leaves of
![]() ${\mathcal F}$
are graphs above
${\mathcal F}$
are graphs above
![]() $(\alpha , \beta )$
.
$(\alpha , \beta )$
.
Another result of the transversality of
![]() ${\mathcal F}$
and the vertical foliation
${\mathcal F}$
and the vertical foliation
![]() ${\mathcal G}_0$
is that the foliation
${\mathcal G}_0$
is that the foliation
![]() ${\mathcal G}=\Phi ^{-1}({\mathcal G}_0)$
is a foliation of
${\mathcal G}=\Phi ^{-1}({\mathcal G}_0)$
is a foliation of
![]() ${\mathcal U}$
that is transverse to the standard (‘horizontal’) foliation
${\mathcal U}$
that is transverse to the standard (‘horizontal’) foliation
![]() ${\mathcal F}_0=\Phi ^{-1}({\mathcal F})$
. This means precisely that the foliation
${\mathcal F}_0=\Phi ^{-1}({\mathcal F})$
. This means precisely that the foliation
![]() ${\mathcal G}$
is a foliation by graphs of maps
${\mathcal G}$
is a foliation by graphs of maps
![]() $\zeta _\theta : I=\pi _2({\mathcal U})\rightarrow \pi _1({\mathcal U})$
. Hence there exists a continuous function
$\zeta _\theta : I=\pi _2({\mathcal U})\rightarrow \pi _1({\mathcal U})$
. Hence there exists a continuous function
![]() $v:{\mathcal W}\rightarrow \mathbb {R}$
that admits a continuous derivative with respect to r such that the foliation
$v:{\mathcal W}\rightarrow \mathbb {R}$
that admits a continuous derivative with respect to r such that the foliation
![]() ${\mathcal G}$
is the foliation by graphs
${\mathcal G}$
is the foliation by graphs
![]() $\Phi ^{-1}(\pi _1^{-1}(\{\theta \}))$
of
$\Phi ^{-1}(\pi _1^{-1}(\{\theta \}))$
of
![]() $\zeta _\theta : r\mapsto \theta +({\partial v}/{\partial r})(\theta , r)$
. Observe that by definition of
$\zeta _\theta : r\mapsto \theta +({\partial v}/{\partial r})(\theta , r)$
. Observe that by definition of
![]() $\zeta _\theta $
, we have
$\zeta _\theta $
, we have
![]() $\Phi (\zeta _\theta (c), c)=(\theta ,\eta _c(\theta ))$
. As a result, every map
$\Phi (\zeta _\theta (c), c)=(\theta ,\eta _c(\theta ))$
. As a result, every map
![]() $\theta \mapsto \zeta _\theta (c)$
is a homeomorphism onto its image.
$\theta \mapsto \zeta _\theta (c)$
is a homeomorphism onto its image.

We now use the preservation of the area. We fix
![]() $\theta _1<\theta _2$
in
$\theta _1<\theta _2$
in
![]() $\pi _1({\mathcal V})$
and
$\pi _1({\mathcal V})$
and
![]() $c_1<c_2$
in
$c_1<c_2$
in
![]() $\pi _2({\mathcal U})$
such that the domain
$\pi _2({\mathcal U})$
such that the domain
![]() $D_1$
delimited by the horizontals
$D_1$
delimited by the horizontals
![]() $\pi _2^{-1}( \{ c_1\})$
,
$\pi _2^{-1}( \{ c_1\})$
,
![]() $\pi _2^{-1}( \{ c_2\})$
, the graph of
$\pi _2^{-1}( \{ c_2\})$
, the graph of
![]() $c\in [c_1, c_2]\mapsto \zeta _{\theta _1}(c)$
and the graph of
$c\in [c_1, c_2]\mapsto \zeta _{\theta _1}(c)$
and the graph of
![]() $c\in [c_1, c_2]\mapsto \zeta _{\theta _2}(c)$
is contained in
$c\in [c_1, c_2]\mapsto \zeta _{\theta _2}(c)$
is contained in
![]() ${\mathcal U}$
. Because
${\mathcal U}$
. Because
![]() $\Phi $
is a symplectic homeomorphism,
$\Phi $
is a symplectic homeomorphism,
![]() $\Phi $
preserves the area and so
$\Phi $
preserves the area and so
![]() $D_1$
and
$D_1$
and
![]() $\Phi (D_1)$
have the same area. Observe that
$\Phi (D_1)$
have the same area. Observe that
![]() $\Phi (D_1)$
is the domain delimited by the graphs of
$\Phi (D_1)$
is the domain delimited by the graphs of
![]() $\eta _{c_1}$
,
$\eta _{c_1}$
,
![]() $\eta _{c_2}$
and the verticals
$\eta _{c_2}$
and the verticals
![]() $\pi _1^{-1}(\{\theta _1\})$
and
$\pi _1^{-1}(\{\theta _1\})$
and
![]() $\pi _1^{-1}(\{ \theta _2\})$
. This can be written
$\pi _1^{-1}(\{ \theta _2\})$
. This can be written
 $$ \begin{align*} &\int_{c_1}^{c_2}\bigg( \bigg(\theta_2+\frac{\partial v}{\partial c} (\theta_2,c)\bigg)-\bigg(\theta_1+\frac{\partial v}{\partial c} (\theta_1,c)\bigg)\bigg)\, dc\\ &\quad=\int_{\theta_1}^{\theta_2}\bigg(\bigg(c_2+\frac{\partial u}{\partial \theta} (\theta,c_2)\bigg) - \bigg(c_1+\frac{\partial u}{\partial \theta} (\theta,c_1)\bigg)\bigg)\,d\theta .\end{align*} $$
$$ \begin{align*} &\int_{c_1}^{c_2}\bigg( \bigg(\theta_2+\frac{\partial v}{\partial c} (\theta_2,c)\bigg)-\bigg(\theta_1+\frac{\partial v}{\partial c} (\theta_1,c)\bigg)\bigg)\, dc\\ &\quad=\int_{\theta_1}^{\theta_2}\bigg(\bigg(c_2+\frac{\partial u}{\partial \theta} (\theta,c_2)\bigg) - \bigg(c_1+\frac{\partial u}{\partial \theta} (\theta,c_1)\bigg)\bigg)\,d\theta .\end{align*} $$
It follows that
 $$ \begin{align*} &u(\theta_2,c_2)-u(\theta_1,c_2)-u(\theta_2,c_1)+u(\theta_1,c_1) \\ &\quad=v(\theta_2,c_2) -v(\theta_2,c_1) -v(\theta_1,c_2) +v(\theta_1,c_1). \end{align*} $$
$$ \begin{align*} &u(\theta_2,c_2)-u(\theta_1,c_2)-u(\theta_2,c_1)+u(\theta_1,c_1) \\ &\quad=v(\theta_2,c_2) -v(\theta_2,c_1) -v(\theta_1,c_2) +v(\theta_1,c_1). \end{align*} $$
Evaluating for
![]() $\theta _1=0$
we find
$\theta _1=0$
we find
Finally, as v admits a continuous partial derivative with respect to c, we conclude that
![]() $({\partial u}/{\partial c})(\theta , c) = ({\partial v}/{\partial c})(\theta , c)-({\partial v}/{\partial c})(0, c)$
exists and is continuous. Hence u is
$({\partial u}/{\partial c})(\theta , c) = ({\partial v}/{\partial c})(\theta , c)-({\partial v}/{\partial c})(0, c)$
exists and is continuous. Hence u is
![]() $C^1$
. Moreover, every map
$C^1$
. Moreover, every map
![]() $\theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)= \zeta _c(\theta )-({\partial v}/{\partial c})(0, c)$
is a homeomorphism onto its image and we have established the first implication.
$\theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)= \zeta _c(\theta )-({\partial v}/{\partial c})(0, c)$
is a homeomorphism onto its image and we have established the first implication.
4.2 Proof of the second implication
We assume that there exists a
![]() $C^1$
map
$C^1$
map
![]() $u : {{\mathcal W}} \to \mathbb {R}$
such that:
$u : {{\mathcal W}} \to \mathbb {R}$
such that:
-
•
 $u(0,c) = 0$
for all
$u(0,c) = 0$
for all
 $c\in I$
where
$c\in I$
where
 $I=(c_-, c_+)$
or
$I=(c_-, c_+)$
or
 $I=\mathbb {R}$
;
$I=\mathbb {R}$
; -
•
 $\eta _c(\theta ) = c+ ({\partial u}/{\partial \theta })(\theta ,c)$
for all
$\eta _c(\theta ) = c+ ({\partial u}/{\partial \theta })(\theta ,c)$
for all
 $(\theta , c) \in {\mathcal W}$
;
$(\theta , c) \in {\mathcal W}$
; -
• for all
 $c\in I$
, the map
$c\in I$
, the map
 $h_c :\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
is increasing.
$h_c :\theta \mapsto \theta + ({\partial u}/{\partial c})(\theta , c)$
is increasing.
Then we can define a unique homeomorphism
![]() $\Phi $
by
$\Phi $
by
 $$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
$$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
We first prove the result when
![]() ${\mathcal U}=\mathbb {A}$
. Let
${\mathcal U}=\mathbb {A}$
. Let
![]() $v:\mathbb {R}^2\rightarrow \mathbb {R}_+$
be the
$v:\mathbb {R}^2\rightarrow \mathbb {R}_+$
be the
![]() $C^\infty $
function with support in
$C^\infty $
function with support in
![]() $B(0, 1)$
defined by
$B(0, 1)$
defined by
![]() $v(\theta , c) = a \exp ((1-\|(\theta , c)\|)^{-2})$
for
$v(\theta , c) = a \exp ((1-\|(\theta , c)\|)^{-2})$
for
![]() $(\theta , c) \in B(0,1)$
and where a is such that
$(\theta , c) \in B(0,1)$
and where a is such that
![]() $\int \!v=1$
. We denote by
$\int \!v=1$
. We denote by
![]() $v_\varepsilon $
the function
$v_\varepsilon $
the function
![]() $v_\varepsilon (x)=({1}/{\varepsilon ^2})v({x}/{\varepsilon })$
.
$v_\varepsilon (x)=({1}/{\varepsilon ^2})v({x}/{\varepsilon })$
.
For every
![]() $\varepsilon>0$
, we define
$\varepsilon>0$
, we define
where we recall the convolution formula
Then when
![]() $\varepsilon $
tends to
$\varepsilon $
tends to
![]() $0$
, the functions
$0$
, the functions
![]() $U_\varepsilon $
tend to U in the
$U_\varepsilon $
tend to U in the
![]() $C^1$
compact-open topology. Moreover,
$C^1$
compact-open topology. Moreover,
![]() $U_\varepsilon $
is
$U_\varepsilon $
is
![]() $1$
-periodic in
$1$
-periodic in
![]() $\theta $
and smooth. Observe that for every
$\theta $
and smooth. Observe that for every
![]() $\theta $
, the function
$\theta $
, the function
![]() $c\mapsto c+({\partial u}/{\partial \theta })(\theta ,c)$
is increasing. We deduce that the convolution
$c\mapsto c+({\partial u}/{\partial \theta })(\theta ,c)$
is increasing. We deduce that the convolution
![]() $c\mapsto c+({\partial U_\varepsilon }/{\partial \theta })(\theta ,c)$
is a
$c\mapsto c+({\partial U_\varepsilon }/{\partial \theta })(\theta ,c)$
is a
![]() $C^\infty $
diffeomorphism as it is a mean of
$C^\infty $
diffeomorphism as it is a mean of
![]() $C^\infty $
diffeomorphisms thanks to Lemma 4.1. Finally, the maps
$C^\infty $
diffeomorphisms thanks to Lemma 4.1. Finally, the maps
![]() $F_\varepsilon : (\theta , c)\mapsto (\theta , c+({\partial U_\varepsilon }/{\partial \theta })(\theta , c))$
define
$F_\varepsilon : (\theta , c)\mapsto (\theta , c+({\partial U_\varepsilon }/{\partial \theta })(\theta , c))$
define
![]() $C^\infty $
foliations that converge to the initial foliation
$C^\infty $
foliations that converge to the initial foliation
![]() $F_0: (\theta , c)\mapsto (\theta , c+({\partial u}/{\partial \theta })(\theta , c))$
for the
$F_0: (\theta , c)\mapsto (\theta , c+({\partial u}/{\partial \theta })(\theta , c))$
for the
![]() $C^0$
compact-open topology when
$C^0$
compact-open topology when
![]() $\varepsilon $
tends to
$\varepsilon $
tends to
![]() $0$
.
$0$
.
Observe that the
![]() $h_c : \theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
are assumed to be increasing. We deduce that the maps
$h_c : \theta \mapsto \theta +({\partial u}/{\partial c})(\theta , c)$
are assumed to be increasing. We deduce that the maps
![]() $G_\varepsilon : (\theta , c)\mapsto (\theta +({\partial U_\varepsilon }/{\partial c})(\theta ,c), c)$
are
$G_\varepsilon : (\theta , c)\mapsto (\theta +({\partial U_\varepsilon }/{\partial c})(\theta ,c), c)$
are
![]() $C^\infty $
diffeomorphisms of
$C^\infty $
diffeomorphisms of
![]() $\mathbb {A}$
that converge for the
$\mathbb {A}$
that converge for the
![]() $C^0$
compact-open topology to
$C^0$
compact-open topology to
![]() $G_0:(\theta , c)\mapsto (\theta +({\partial u}/{\partial c})(\theta , c), c)$
.
$G_0:(\theta , c)\mapsto (\theta +({\partial u}/{\partial c})(\theta , c), c)$
.
Finally, the maps
![]() ${\mathcal H}_\varepsilon = F_\varepsilon \circ G_\varepsilon ^{-1}$
are
${\mathcal H}_\varepsilon = F_\varepsilon \circ G_\varepsilon ^{-1}$
are
![]() $C^\infty $
diffeomorphisms of
$C^\infty $
diffeomorphisms of
![]() $\mathbb {A}$
that converge for the
$\mathbb {A}$
that converge for the
![]() $C^0$
compact-open topology to
$C^0$
compact-open topology to
![]() $F_0\circ G_0^{-1}=\Phi $
. Moreover, because they are defined via generating functions
$F_0\circ G_0^{-1}=\Phi $
. Moreover, because they are defined via generating functions
![]() $U_\varepsilon $
in the classical sense, we know that the diffeomorphisms
$U_\varepsilon $
in the classical sense, we know that the diffeomorphisms
![]() ${\mathcal H}_\varepsilon $
are all exact symplectic.
${\mathcal H}_\varepsilon $
are all exact symplectic.
This means precisely that
![]() $\Phi $
is an exact symplectic homeomorphism.
$\Phi $
is an exact symplectic homeomorphism.
We now deal with the local case when
![]() ${\mathcal U}\neq \mathbb {A}$
. The computation from the first implication (with
${\mathcal U}\neq \mathbb {A}$
. The computation from the first implication (with
![]() $u=v$
) shows that
$u=v$
) shows that
![]() $\Phi $
is area preserving. We conclude with the next proposition.
$\Phi $
is area preserving. We conclude with the next proposition.
Proposition 4.1. Let
![]() $\psi : {\mathcal U} \to {\mathcal V}$
be a homeomorphism that preserves the Lebesgue measure
$\psi : {\mathcal U} \to {\mathcal V}$
be a homeomorphism that preserves the Lebesgue measure
![]() $\lambda $
. Then there exists a sequence
$\lambda $
. Then there exists a sequence
![]() $\psi _n : {\mathcal U} \to {\mathcal V}$
of area-preserving diffeomorphisms that converges to
$\psi _n : {\mathcal U} \to {\mathcal V}$
of area-preserving diffeomorphisms that converges to
![]() $\psi $
for the compact-open topology.
$\psi $
for the compact-open topology.
Proof. As
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() ${\mathcal V}$
are bounded and simply connected they are diffeomorphic. Let
${\mathcal V}$
are bounded and simply connected they are diffeomorphic. Let
![]() $\phi _0 : {\mathcal V} \to {\mathcal U}$
be a diffeomorphism. As
$\phi _0 : {\mathcal V} \to {\mathcal U}$
be a diffeomorphism. As
![]() $\phi _{0*}\lambda ({\mathcal U}) = \lambda ({\mathcal V}) = \lambda ({\mathcal U})$
(because
$\phi _{0*}\lambda ({\mathcal U}) = \lambda ({\mathcal V}) = \lambda ({\mathcal U})$
(because
![]() $\psi $
preserves
$\psi $
preserves
![]() $\lambda $
) we can apply [Reference Greene and Shiohama9, Theorem 1] to obtain a diffeomorphism
$\lambda $
) we can apply [Reference Greene and Shiohama9, Theorem 1] to obtain a diffeomorphism
![]() $\phi _1 : {\mathcal U} \to {\mathcal U}$
such that
$\phi _1 : {\mathcal U} \to {\mathcal U}$
such that
![]() $\phi _{1*} (\phi _{0*}\lambda ) = \lambda $
.
$\phi _{1*} (\phi _{0*}\lambda ) = \lambda $
.
Let
![]() $S\subset \mathbb {R}^3$
be a two-dimensional Euclidean sphere that has same total Lebesgue area as
$S\subset \mathbb {R}^3$
be a two-dimensional Euclidean sphere that has same total Lebesgue area as
![]() ${\mathcal U}$
. We denote by
${\mathcal U}$
. We denote by
![]() $\lambda _S$
the Lebesgue area on S. Let
$\lambda _S$
the Lebesgue area on S. Let
![]() $N\in S$
be a point. As
$N\in S$
be a point. As
![]() $S\setminus \{N\}$
is diffeomorphic to
$S\setminus \{N\}$
is diffeomorphic to
![]() ${\mathcal U}$
, arguing as before, and again using [Reference Greene and Shiohama9] yields a diffeomorphism
${\mathcal U}$
, arguing as before, and again using [Reference Greene and Shiohama9] yields a diffeomorphism
![]() $\phi _2 : {\mathcal U} \to S\setminus \{N\} $
such that
$\phi _2 : {\mathcal U} \to S\setminus \{N\} $
such that
![]() $\phi _{2*}\lambda = \lambda _S$
.
$\phi _{2*}\lambda = \lambda _S$
.
Set
![]() $\Psi = \phi _2 \circ \phi _1 \circ \phi _0 \circ \psi \circ \phi _2^{-1}$
, a homeomorphism of
$\Psi = \phi _2 \circ \phi _1 \circ \phi _0 \circ \psi \circ \phi _2^{-1}$
, a homeomorphism of
![]() $S\setminus \{N\} $
that preserves
$S\setminus \{N\} $
that preserves
![]() $\lambda _S$
. It extends to a homeomorphism
$\lambda _S$
. It extends to a homeomorphism
![]() $\widetilde \Psi $
of S by setting
$\widetilde \Psi $
of S by setting
![]() $\widetilde \Psi (N)=N$
that still preserves
$\widetilde \Psi (N)=N$
that still preserves
![]() $\lambda _S$
.
$\lambda _S$
.
We may now apply a classical dynamical systems result to approximate
![]() $\widetilde \Psi $
by area-preserving diffeomorphisms
$\widetilde \Psi $
by area-preserving diffeomorphisms
![]() $(\widetilde \Psi _n)_{n>0}$
of S ([Reference Oh17]; see also [Reference Lefeuvre13] for a simpler proof adapted from an idea of Sikorav). Up to composing by rotations of S (that preserve
$(\widetilde \Psi _n)_{n>0}$
of S ([Reference Oh17]; see also [Reference Lefeuvre13] for a simpler proof adapted from an idea of Sikorav). Up to composing by rotations of S (that preserve
![]() $\lambda _S)$
we may assume furthermore that
$\lambda _S)$
we may assume furthermore that
![]() $\widetilde \Psi _n(N)=N$
for all
$\widetilde \Psi _n(N)=N$
for all
![]() $n>0$
. Therefore by restriction, they give rise to
$n>0$
. Therefore by restriction, they give rise to
![]() $(\Psi _n)_{n>0}$
that are diffeomorphisms of
$(\Psi _n)_{n>0}$
that are diffeomorphisms of
![]() $S\setminus \{N\}$
that uniformly converge to
$S\setminus \{N\}$
that uniformly converge to
![]() $\Psi $
.
$\Psi $
.
Finally, setting
![]() $\psi _n = \phi _0^{-1}\circ \phi _1^{-1}\circ \phi _2^{-1} \Psi _n\circ \phi _2$
yields a family
$\psi _n = \phi _0^{-1}\circ \phi _1^{-1}\circ \phi _2^{-1} \Psi _n\circ \phi _2$
yields a family
![]() $(\psi _n)_{n>0}$
of area-preserving diffeomorphisms that converge to
$(\psi _n)_{n>0}$
of area-preserving diffeomorphisms that converge to
![]() $\psi $
for the compact–open topology.
$\psi $
for the compact–open topology.
Lemma 4.1. Let
![]() $f : \mathbb {R}\to \mathbb {R}$
be a non-negative, non-trivial, smooth, compactly supported in
$f : \mathbb {R}\to \mathbb {R}$
be a non-negative, non-trivial, smooth, compactly supported in
![]() $[-M, M]$
and even function such that
$[-M, M]$
and even function such that
![]() $ f' \leq 0$
on
$ f' \leq 0$
on
![]() $[0,+\infty )$
. Then:
$[0,+\infty )$
. Then:
-
• if
 $g : \mathbb {R} \to \mathbb {R}$
is an increasing function,
$g : \mathbb {R} \to \mathbb {R}$
is an increasing function,
 $f*g$
is an increasing
$f*g$
is an increasing
 $C^\infty $
diffeomorphism onto its image; if, moreover, g is a homeomorphism of
$C^\infty $
diffeomorphism onto its image; if, moreover, g is a homeomorphism of
 $\mathbb {R}$
, then
$\mathbb {R}$
, then
 $f*g$
is a
$f*g$
is a
 $C^\infty $
diffeomorphism of
$C^\infty $
diffeomorphism of
 $\mathbb {R}$
;
$\mathbb {R}$
; -
• if
 $g:[a-M, b+M]\rightarrow \mathbb {R}$
is an increasing function, we can define
$g:[a-M, b+M]\rightarrow \mathbb {R}$
is an increasing function, we can define
 $f*g:[a, b]\rightarrow \mathbb {R}$
that is an increasing
$f*g:[a, b]\rightarrow \mathbb {R}$
that is an increasing
 $C^\infty $
diffeomorphism onto its image.
$C^\infty $
diffeomorphism onto its image.
Proof. We only prove the first point, the second one being very similar. As f is smooth and compactly supported,
![]() $f*g$
is well defined and smooth. As f is even,
$f*g$
is well defined and smooth. As f is even,
![]() $f'$
is odd. Just notice that
$f'$
is odd. Just notice that
 $$ \begin{align*}(f*g)'(x) = \int_{\mathbb{R}} f'(y)g(x-y)\, dy = \int_0^{+\infty} f'(y) (g(x-y)-g(x+y))\, dy.\end{align*} $$
$$ \begin{align*}(f*g)'(x) = \int_{\mathbb{R}} f'(y)g(x-y)\, dy = \int_0^{+\infty} f'(y) (g(x-y)-g(x+y))\, dy.\end{align*} $$
Then
![]() $f*g$
is an increasing diffeomorphism onto its image as
$f*g$
is an increasing diffeomorphism onto its image as
![]() $g(x-y)-g(x+y) <0$
and
$g(x-y)-g(x+y) <0$
and
![]() $f'(y) \leq 0$
and
$f'(y) \leq 0$
and
![]() $f'$
is not the zero function.
$f'$
is not the zero function.
Let us now assume that
![]() $\lim _{x\to +\infty } g(x) = +\infty $
. We will prove that
$\lim _{x\to +\infty } g(x) = +\infty $
. We will prove that
![]() $\lim _{x\to +\infty } f*g(x) = +\infty $
. Let
$\lim _{x\to +\infty } f*g(x) = +\infty $
. Let
![]() $M>0$
such that the support of f is included in
$M>0$
such that the support of f is included in
![]() $[-M,M]$
. Let
$[-M,M]$
. Let
![]() $A>0$
and
$A>0$
and
![]() $B\in \mathbb {R}$
such that
$B\in \mathbb {R}$
such that
![]() $A< g(x)$
as soon as
$A< g(x)$
as soon as
![]() $x>B$
. Then if
$x>B$
. Then if
![]() $x>M+B$
,
$x>M+B$
,
 $$ \begin{align*}f*g(x) = \int_{-M}^M f(y)g(x-y)\,dy>A\int_{\mathbb{R}} f(y)\,dy.\end{align*} $$
$$ \begin{align*}f*g(x) = \int_{-M}^M f(y)g(x-y)\,dy>A\int_{\mathbb{R}} f(y)\,dy.\end{align*} $$
This proves our result as
![]() $\int _{\mathbb {R}} f(y)\,dy>0$
.
$\int _{\mathbb {R}} f(y)\,dy>0$
.
5 Proof of Proposition 1.1 and Corollary 1.4
5.1 Proof of Proposition 1.1: bi-Lipschitz foliations with
 $C^1$
generating functions are straightenable
$C^1$
generating functions are straightenable
Let
![]() $u:\mathbb {A}\rightarrow \mathbb {R}$
be the
$u:\mathbb {A}\rightarrow \mathbb {R}$
be the
![]() $C^1$
generating function of a continuous foliation of
$C^1$
generating function of a continuous foliation of
![]() $\mathbb {A}$
into graphs. We recall the following result due to Minguzzi [Reference Minguzzi16].
$\mathbb {A}$
into graphs. We recall the following result due to Minguzzi [Reference Minguzzi16].
Theorem. (Minguzzi)
Let
![]() $\Omega $
be an open subset of
$\Omega $
be an open subset of
![]() $\mathbb {R}^2$
and let
$\mathbb {R}^2$
and let
![]() $f\in C^1(\Omega , \mathbb {R})$
. Then the following conditions are equivalent:
$f\in C^1(\Omega , \mathbb {R})$
. Then the following conditions are equivalent:
-
(1) for every x, the partial derivative
 $({\partial f}/{\partial x})(x,\cdot )$
is locally Lipschitz, locally uniformly with respect to x;
$({\partial f}/{\partial x})(x,\cdot )$
is locally Lipschitz, locally uniformly with respect to x; -
(2) for every y, the partial derivative
 $({\partial f}/{\partial y})(\cdot ,y)$
is locally Lipschitz, locally uniformly with respect to y.
$({\partial f}/{\partial y})(\cdot ,y)$
is locally Lipschitz, locally uniformly with respect to y.
If they hold true, then on a subset
![]() $E\subset \Omega $
with full Lebesgue measure in
$E\subset \Omega $
with full Lebesgue measure in
![]() $\Omega $
,
$\Omega $
,
![]() ${\partial ^2f}/{\partial x\partial y}$
and
${\partial ^2f}/{\partial x\partial y}$
and
![]() ${\partial ^2f}/{\partial y\partial x}$
exist and are equal.
${\partial ^2f}/{\partial y\partial x}$
exist and are equal.
5.1.1 Proof of the first implication
We assume that the invariant foliation is K-Lipschitz on a compact
![]() ${\mathcal K} =\{ (\theta , \eta _c(\theta )); \theta \in \mathbb {T}, c\in [a, b]\}$
, which means
${\mathcal K} =\{ (\theta , \eta _c(\theta )); \theta \in \mathbb {T}, c\in [a, b]\}$
, which means
As
![]() $\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)$
, this means that
$\eta _c(\theta )=c+({\partial u}/{\partial \theta })(\theta , c)$
, this means that
![]() $({\partial u}/{\partial \theta })(\theta , \cdot )$
is locally Lipschitz, locally uniformly with respect to
$({\partial u}/{\partial \theta })(\theta , \cdot )$
is locally Lipschitz, locally uniformly with respect to
![]() $\theta $
. Hence, by Minguzzi’s theorem, for every
$\theta $
. Hence, by Minguzzi’s theorem, for every
![]() $c\in (a, b)$
,
$c\in (a, b)$
,
![]() $({\partial u}/{\partial c})(\cdot , c)$
is locally Lipschitz, locally uniformly with respect to c, and at almost all
$({\partial u}/{\partial c})(\cdot , c)$
is locally Lipschitz, locally uniformly with respect to c, and at almost all
![]() $(\theta , c)\in \mathbb {T}\times (a, b)$
we have that
$(\theta , c)\in \mathbb {T}\times (a, b)$
we have that
![]() ${\partial ^2u}/{\partial c\partial \theta }$
and
${\partial ^2u}/{\partial c\partial \theta }$
and
![]() ${\partial ^2u}/{\partial \theta \partial c}$
exist and are equal and uniformly bounded.
${\partial ^2u}/{\partial \theta \partial c}$
exist and are equal and uniformly bounded.
Hence
![]() $h_c=Id_{\mathbb {T}}+ ({\partial u}/{\partial c})(\cdot ,c )$
is locally uniformly Lipschitz and because of Inequality (19), we have Lebesgue almost everywhere
$h_c=Id_{\mathbb {T}}+ ({\partial u}/{\partial c})(\cdot ,c )$
is locally uniformly Lipschitz and because of Inequality (19), we have Lebesgue almost everywhere
 $$ \begin{align} \frac{\partial^2u}{\partial \theta\partial c}(\theta, c)= \frac{\partial^2u}{\partial c\partial \theta}(\theta, c)=\frac{\partial \eta}{\partial c}(\theta_0, c_0)-1\in \bigg[\!-1+\frac{1}{K}, -1+K\bigg]=[k_-, k_+].\end{align} $$
$$ \begin{align} \frac{\partial^2u}{\partial \theta\partial c}(\theta, c)= \frac{\partial^2u}{\partial c\partial \theta}(\theta, c)=\frac{\partial \eta}{\partial c}(\theta_0, c_0)-1\in \bigg[\!-1+\frac{1}{K}, -1+K\bigg]=[k_-, k_+].\end{align} $$
This implies that
![]() $h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta , c)$
defines a
$h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta , c)$
defines a
![]() $({1}/{K}, K)$
-bi-Lipschitz homeomorphism of
$({1}/{K}, K)$
-bi-Lipschitz homeomorphism of
![]() $\mathbb {T}$
for almost every
$\mathbb {T}$
for almost every
![]() $c\in [a, b]$
and then for all
$c\in [a, b]$
and then for all
![]() $c\in [a, b]$
by continuity. By Theorem 1.3, we deduce that u is the generating function of an exact symplectic homeomorphism
$c\in [a, b]$
by continuity. By Theorem 1.3, we deduce that u is the generating function of an exact symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the invariant foliation onto the standard one.
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the invariant foliation onto the standard one.
5.1.2 Proof of the second implication
We assume that the map u is
![]() $C^1$
with
$C^1$
with
![]() ${\partial u}/{\partial \theta }$
locally Lipschitz continuous and
${\partial u}/{\partial \theta }$
locally Lipschitz continuous and
![]() ${\partial u}/{\partial c}$
uniformly Lipschitz in the variable
${\partial u}/{\partial c}$
uniformly Lipschitz in the variable
![]() $\theta $
on any compact set of cs, and there exist two constants
$\theta $
on any compact set of cs, and there exist two constants
![]() $k_+>k_->-1$
such that
$k_+>k_->-1$
such that
![]() $({\partial ^2 u}/{\partial \theta \partial c})(\theta ,c)\in [k_-, k_+]$
almost everywhere. Because
$({\partial ^2 u}/{\partial \theta \partial c})(\theta ,c)\in [k_-, k_+]$
almost everywhere. Because
![]() ${\partial u}/{\partial c}$
is uniformly Lipschitz in the variable
${\partial u}/{\partial c}$
is uniformly Lipschitz in the variable
![]() $\theta $
on any compact set of cs, we can apply the Minguzzi theorem and equation (20) which implies that the foliation is bi-Lipschitz.
$\theta $
on any compact set of cs, we can apply the Minguzzi theorem and equation (20) which implies that the foliation is bi-Lipschitz.
5.2 Proof of Corollary 1.4
Let
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $r\mapsto f_r$
be a
$r\mapsto f_r$
be a
![]() $C^k$
-foliation in graphs and let u be its generating function. As
$C^k$
-foliation in graphs and let u be its generating function. As
![]() $k\geq 1$
, the foliation is Lipschitz when restricted to every compact set. Hence we can use Proposition 1.1. In this case, u is the generating function of an exact symplectic homeomorphism
$k\geq 1$
, the foliation is Lipschitz when restricted to every compact set. Hence we can use Proposition 1.1. In this case, u is the generating function of an exact symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one and we have
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one and we have
 $$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
$$ \begin{align*}\Phi\bigg(\theta + \frac{\partial u}{\partial c}(\theta , c), c\bigg)=\bigg(\theta, c+ \frac{\partial u}{\partial \theta}(\theta,c)\bigg).\end{align*} $$
Moreover, u is
![]() $C^k$
, hence
$C^k$
, hence
![]() $F_0(\theta , c)=(\theta , c+({\partial u}/{\partial \theta })(\theta , c))$
defines a
$F_0(\theta , c)=(\theta , c+({\partial u}/{\partial \theta })(\theta , c))$
defines a
![]() $C^{k-1}$
homeomorphism that is locally bi-Lipschitz, hence a
$C^{k-1}$
homeomorphism that is locally bi-Lipschitz, hence a
![]() $C^{k-1}$
diffeomorphism.
$C^{k-1}$
diffeomorphism.
Also
![]() $h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta , c)$
is
$h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta , c)$
is
![]() $C^{k-1}$
in
$C^{k-1}$
in
![]() $(\theta , c)$
. Observe that every
$(\theta , c)$
. Observe that every
![]() $h_c$
is a bi-Lipschitz homeomorphism that is
$h_c$
is a bi-Lipschitz homeomorphism that is
![]() $C^{k-1}$
, hence
$C^{k-1}$
, hence
![]() $G_0: (\theta , c)\mapsto (h_c(\theta ), c)$
is also a
$G_0: (\theta , c)\mapsto (h_c(\theta ), c)$
is also a
![]() $C^{k-1}$
diffeomorphism and then
$C^{k-1}$
diffeomorphism and then
![]() $\Phi =F_0\circ G_0^{-1}$
is a
$\Phi =F_0\circ G_0^{-1}$
is a
![]() $C^{k-1}$
symplectic diffeomorphism (where a
$C^{k-1}$
symplectic diffeomorphism (where a
![]() $C^0$
-diffeomorphism is a homeomorphism).
$C^0$
-diffeomorphism is a homeomorphism).
6 More results on symplectic homeomorphisms that are
 $C^0$
-integrable
$C^0$
-integrable
6.1 Proof of Proposition 1.2
Let
![]() $f:\mathbb {A} \to \mathbb {A}$
be an exact symplectic homeomorphism. We assume that f has an invariant foliation
$f:\mathbb {A} \to \mathbb {A}$
be an exact symplectic homeomorphism. We assume that f has an invariant foliation
![]() ${\mathcal F}$
into
${\mathcal F}$
into
![]() $C^0$
graphs that is symplectically homeomorphic (by
$C^0$
graphs that is symplectically homeomorphic (by
![]() $\Phi ^{-1} : \mathbb {A} \to \mathbb {A}$
) to the standard foliation
$\Phi ^{-1} : \mathbb {A} \to \mathbb {A}$
) to the standard foliation
![]() ${\mathcal F}_0=\Phi ^{-1}({\mathcal F})$
. Then the standard foliation is invariant by the exact symplectic homeomorphism
${\mathcal F}_0=\Phi ^{-1}({\mathcal F})$
. Then the standard foliation is invariant by the exact symplectic homeomorphism
![]() $g=\Phi ^{-1}\circ f\circ \Phi $
. Hence we have
$g=\Phi ^{-1}\circ f\circ \Phi $
. Hence we have
As g is area preserving, for every
![]() $\theta \in [0, 1]$
and every
$\theta \in [0, 1]$
and every
![]() $r_1<r_2$
, the area of
$r_1<r_2$
, the area of
![]() $[0, \theta ]\times [r_1, r_2]$
is equal to the area of
$[0, \theta ]\times [r_1, r_2]$
is equal to the area of
![]() $g( [0, \theta ]\times [r_1, r_2])$
, that is,
$g( [0, \theta ]\times [r_1, r_2])$
, that is,
 $$ \begin{align*}\theta(r_2-r_1)=\int_{r_1}^{r_2} (g_1(\theta, r)-g_1(0, r))\,dr.\end{align*} $$
$$ \begin{align*}\theta(r_2-r_1)=\int_{r_1}^{r_2} (g_1(\theta, r)-g_1(0, r))\,dr.\end{align*} $$
Dividing by
![]() $r_2-r_1$
and taking the limit when
$r_2-r_1$
and taking the limit when
![]() $r_2$
tends to
$r_2$
tends to
![]() $r_1$
, we obtain
$r_1$
, we obtain
This proves the proposition for
![]() $\rho =g_1(0, \cdot )$
.
$\rho =g_1(0, \cdot )$
.
6.2 Proof of Corollary 1.5
The ‘if’ part is obvious by Proposition 1.2.
Let us prove the ‘only if’ part, that is, we assume f is
![]() $C^0$
-integrable with the dynamics on each leaf conjugate to a rotation. We denote by
$C^0$
-integrable with the dynamics on each leaf conjugate to a rotation. We denote by
![]() $u : \mathbb {A} \to \mathbb {R}$
the map given by Theorem 1.1 and which enjoys the properties of Theorem 2.1. Hence
$u : \mathbb {A} \to \mathbb {R}$
the map given by Theorem 1.1 and which enjoys the properties of Theorem 2.1. Hence
![]() $h_c:\theta \mapsto \theta +({\partial u}/{\partial c})(\theta ,c)$
is a semi-conjugation between the projected dynamics
$h_c:\theta \mapsto \theta +({\partial u}/{\partial c})(\theta ,c)$
is a semi-conjugation between the projected dynamics
![]() $g_c: \theta \mapsto \pi _1\circ f(\theta , c+({\partial u}/{\partial \theta })(\theta ,c))$
and the rotation
$g_c: \theta \mapsto \pi _1\circ f(\theta , c+({\partial u}/{\partial \theta })(\theta ,c))$
and the rotation
![]() $R_{\rho (c)}$
of
$R_{\rho (c)}$
of
![]() $\mathbb {T}$
and is even a conjugation when
$\mathbb {T}$
and is even a conjugation when
![]() $\rho (c)$
is rational.
$\rho (c)$
is rational.
If
![]() $\rho (c)$
is irrational, it follows from the hypothesis that
$\rho (c)$
is irrational, it follows from the hypothesis that
![]() $g_c$
is conjugate to a rotation. As the dynamics is minimal, there is up to constants a unique (semi)-conjugacy and then
$g_c$
is conjugate to a rotation. As the dynamics is minimal, there is up to constants a unique (semi)-conjugacy and then
![]() $h_c$
is a true conjugation. We then conclude by using Theorem 1.3.
$h_c$
is a true conjugation. We then conclude by using Theorem 1.3.
6.3 Proof of Corollary 1.6
6.3.1 Arnol’d–Liouville coordinates for f
Let
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic twist diffeomorphism that is Lipschitz integrable with generating function u of its invariant foliation.
$f:\mathbb {A}\rightarrow \mathbb {A}$
be a symplectic twist diffeomorphism that is Lipschitz integrable with generating function u of its invariant foliation.
By Theorem 1.1 and Proposition 1.1, u is the generating function of an exact symplectic homeomorphism
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one, and for every compact subset
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
that maps the standard foliation onto the invariant one, and for every compact subset
![]() ${\mathcal K}\subset \mathbb {A}$
there exist two constants
${\mathcal K}\subset \mathbb {A}$
there exist two constants
![]() $k_+>k_->-1$
such that
$k_+>k_->-1$
such that
![]() ${\partial ^2 u}/{\partial \theta \partial c}\in [k_-, k_+]$
Lebesgue almost everywhere in
${\partial ^2 u}/{\partial \theta \partial c}\in [k_-, k_+]$
Lebesgue almost everywhere in
![]() ${\mathcal K}$
.
${\mathcal K}$
.
By Proposition 1.2, we have
where
![]() $\rho :\mathbb {R}\rightarrow \mathbb {R}$
is continuous. Moreover, because of the twist condition,
$\rho :\mathbb {R}\rightarrow \mathbb {R}$
is continuous. Moreover, because of the twist condition,
![]() $\rho $
is an increasing homeomorphism of
$\rho $
is an increasing homeomorphism of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
6.3.2 Proof that
 $\rho :\mathbb {R}\rightarrow \mathbb {R}$
is a bi-Lipschitz homeomorphism
$\rho :\mathbb {R}\rightarrow \mathbb {R}$
is a bi-Lipschitz homeomorphism
Proposition 6.1. Assume that a
![]() $C^1$
symplectic twist diffeomorphism
$C^1$
symplectic twist diffeomorphism
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
has an invariant locally Lipschitz continuous foliation by graphs
$f:\mathbb {A}\rightarrow \mathbb {A}$
has an invariant locally Lipschitz continuous foliation by graphs
![]() $c\in \mathbb {R}\mapsto \eta _c\in C^{0}(\mathbb {T}, \mathbb {R})$
. Then the map
$c\in \mathbb {R}\mapsto \eta _c\in C^{0}(\mathbb {T}, \mathbb {R})$
. Then the map
![]() $\rho : c\in \mathbb {R}\mapsto \rho (c)$
is a locally bi-Lipschitz homeomorphism.
$\rho : c\in \mathbb {R}\mapsto \rho (c)$
is a locally bi-Lipschitz homeomorphism.
We will use the following lemma.
Lemma 6.1. Let
![]() $f,g : \mathbb {R} \to \mathbb {R}$
be lifts of homeomorphisms of
$f,g : \mathbb {R} \to \mathbb {R}$
be lifts of homeomorphisms of
![]() $\mathbb {T}$
that preserve orientation (implying
$\mathbb {T}$
that preserve orientation (implying
![]() $f(\cdot +1) = f(\cdot ) +1$
and
$f(\cdot +1) = f(\cdot ) +1$
and
![]() $g(\cdot +1) = g(\cdot ) +1$
). Assume that:
$g(\cdot +1) = g(\cdot ) +1$
). Assume that:
-
• either f or g is conjugate to a translation
 $t_\alpha : x \mapsto x+\alpha $
by a homeomorphism h that is a lift of a homeomorphism of
$t_\alpha : x \mapsto x+\alpha $
by a homeomorphism h that is a lift of a homeomorphism of
 $\mathbb {T}$
that preserves orientation;
$\mathbb {T}$
that preserves orientation; -
• h and
 $h^{-1}$
are K-Lipschitz.
$h^{-1}$
are K-Lipschitz.
Then:
-
(1) if there exists
 $d>0$
such that
$d>0$
such that
 $f<g+d$
, then
$f<g+d$
, then
 $\rho (f)\leq \rho (g)+Kd$
;
$\rho (f)\leq \rho (g)+Kd$
; -
(2) if there exists
 $d>0$
such that
$d>0$
such that
 $f+d <g$
then
$f+d <g$
then
 $\rho (f) +{d}/{K}\leq \rho (g)$
.
$\rho (f) +{d}/{K}\leq \rho (g)$
.
Proof. Let us say that
![]() $h\circ g \circ h^{-1} = t_\alpha $
, hence
$h\circ g \circ h^{-1} = t_\alpha $
, hence
![]() $\rho (g) = \alpha $
(the proof when f is conjugate to a translation is the same).
$\rho (g) = \alpha $
(the proof when f is conjugate to a translation is the same).
(1) By hypothesis,
![]() $ f\circ h^{-1}< g\circ h^{-1} +d $
. Using that h is increasing and K-Lipschitz, it follows that for all
$ f\circ h^{-1}< g\circ h^{-1} +d $
. Using that h is increasing and K-Lipschitz, it follows that for all
![]() $ x\in \mathbb {R}$
,
$ x\in \mathbb {R}$
,
Finally, as
![]() $\rho (f) = \rho ( h\circ f\circ h^{-1})$
, we conclude that
$\rho (f) = \rho ( h\circ f\circ h^{-1})$
, we conclude that
(2) By hypothesis,
![]() $ f\circ h^{-1}+d< g\circ h^{-1} $
. Using that h is increasing, it follows that
$ f\circ h^{-1}+d< g\circ h^{-1} $
. Using that h is increasing, it follows that
Because
![]() $h^{-1}$
is K-Lipschitz and increasing, observe that
$h^{-1}$
is K-Lipschitz and increasing, observe that
 $$ \begin{align*} d&=h^{-1}(h(f\circ h^{-1}(x)+d))-h^{-1}(h\circ f\circ h^{-1}(x))\\ &\leq K( h(f\circ h^{-1}(x)+d)-h\circ f\circ h^{-1}(x)). \end{align*} $$
$$ \begin{align*} d&=h^{-1}(h(f\circ h^{-1}(x)+d))-h^{-1}(h\circ f\circ h^{-1}(x))\\ &\leq K( h(f\circ h^{-1}(x)+d)-h\circ f\circ h^{-1}(x)). \end{align*} $$
Then
Hence
![]() $\rho (f)+{d}/{K}\leq \rho (g)$
.
$\rho (f)+{d}/{K}\leq \rho (g)$
.
Proof of Proposition 6.1
The proof is now a direct application of the previous lemma. Indeed, we have seen that when the foliation is K-Lipschitz, if c varies in a compact set
![]() $\mathcal K$
, the dynamics
$\mathcal K$
, the dynamics
![]() $g_c$
are all conjugate to rotations. We have, moreover, proven there exists a constant
$g_c$
are all conjugate to rotations. We have, moreover, proven there exists a constant
![]() $\widetilde K$
such that the conjugating functions
$\widetilde K$
such that the conjugating functions
![]() $h_c$
may be chosen equi-bi-Lipschitz (for
$h_c$
may be chosen equi-bi-Lipschitz (for
![]() $c\in \mathcal K$
) of constant
$c\in \mathcal K$
) of constant
![]() $\widetilde K$
.
$\widetilde K$
.
We denote the minimum and maximum torsions on
![]() ${\mathcal K}$
by
${\mathcal K}$
by
For
![]() $c_1<c_2$
in
$c_1<c_2$
in
![]() $[a, b]$
, we have
$[a, b]$
, we have
and so
and
 $$ \begin{align*}\tilde g_{c_2}(\theta)-\tilde g_{c_1}(\theta)\in \bigg[\frac{b_{\min}}{K}(c_2-c_1), K.{b_{\max}} (c_2-c_1)\bigg].\end{align*} $$
$$ \begin{align*}\tilde g_{c_2}(\theta)-\tilde g_{c_1}(\theta)\in \bigg[\frac{b_{\min}}{K}(c_2-c_1), K.{b_{\max}} (c_2-c_1)\bigg].\end{align*} $$
We deduce from Lemma 6.1 that
6.3.3 Proof of the
 $C^1$
regularity
$C^1$
regularity
Here we prove that
![]() $\Phi :\mathbb {A}\rightarrow \mathbb {A}$
is
$\Phi :\mathbb {A}\rightarrow \mathbb {A}$
is
![]() $C^1$
in the
$C^1$
in the
![]() $\theta $
variable, that the invariant foliation is a
$\theta $
variable, that the invariant foliation is a
![]() $C^1$
lamination and that the dynamics restricted to every leaf is
$C^1$
lamination and that the dynamics restricted to every leaf is
![]() $C^1$
conjugate to a rotation.
$C^1$
conjugate to a rotation.
Let us fix c. Then
![]() $h_c=Id_{\mathbb {T}}+({\partial u}/{\partial c})(\cdot , c)$
is a bi-Lipschitz homeomorphism of
$h_c=Id_{\mathbb {T}}+({\partial u}/{\partial c})(\cdot , c)$
is a bi-Lipschitz homeomorphism of
![]() $\mathbb {T}$
by Proposition 1.1. Then [Reference Arnaud1, Corollary 4] tells us that
$\mathbb {T}$
by Proposition 1.1. Then [Reference Arnaud1, Corollary 4] tells us that
![]() $\eta _c$
is in fact
$\eta _c$
is in fact
![]() $C^1$
(and the two Green bundles coincide along its graphs) and that
$C^1$
(and the two Green bundles coincide along its graphs) and that
![]() $h_c$
is a
$h_c$
is a
![]() $C^1$
diffeomorphism.
$C^1$
diffeomorphism.
Hence all the points of
![]() $\mathbb {A}$
are recurrent. Moreover, as the two Green bundles are equal everywhere, they are continuous. Because they coincide with the tangent space to the foliation, the foliation is a
$\mathbb {A}$
are recurrent. Moreover, as the two Green bundles are equal everywhere, they are continuous. Because they coincide with the tangent space to the foliation, the foliation is a
![]() $C^1$
lamination. This is equivalent to the continuity (in the two variables) of
$C^1$
lamination. This is equivalent to the continuity (in the two variables) of
![]() ${\partial ^2u}/{\partial \theta ^2}$
.
${\partial ^2u}/{\partial \theta ^2}$
.
As
![]() $\Phi (\Theta , c)=(h_c^{-1}(\Theta ), \eta _c\circ h_c^{-1}(\Theta ))$
, we deduce that
$\Phi (\Theta , c)=(h_c^{-1}(\Theta ), \eta _c\circ h_c^{-1}(\Theta ))$
, we deduce that
![]() $\Phi $
is
$\Phi $
is
![]() $C^1$
in the
$C^1$
in the
![]() $\theta $
-direction.
$\theta $
-direction.
Remark. We do not know if
![]() ${\partial ^2u}/{\partial \theta \partial c}$
is continuous, and then if
${\partial ^2u}/{\partial \theta \partial c}$
is continuous, and then if
![]() $c\mapsto h_c$
is continuous for the
$c\mapsto h_c$
is continuous for the
![]() $C^1$
topology.
$C^1$
topology.
7 A strange foliation
We consider the foliation of
![]() $\mathbb {A}$
by the graphs of
$\mathbb {A}$
by the graphs of
![]() $\eta _c(\theta ) = c+ \varepsilon (c)\cos (2\pi \theta )$
where
$\eta _c(\theta ) = c+ \varepsilon (c)\cos (2\pi \theta )$
where
![]() $\varepsilon $
is a contraction (k-Lipschitz with
$\varepsilon $
is a contraction (k-Lipschitz with
![]() $k<1$
) that is not everywhere differentiable. It is a bi-Lipschitz foliation with smooth leaves. Indeed, for all
$k<1$
) that is not everywhere differentiable. It is a bi-Lipschitz foliation with smooth leaves. Indeed, for all
![]() $c<c'$
and
$c<c'$
and
![]() $\theta $
,
$\theta $
,
Observe that the generating function of this foliation is given by
7.1 Proof of Corollaries 1.1–1.3
As u is not
![]() $C^1$
, we deduce from Theorems 1.1 and 1.3 that this foliation cannot be globally straightenable by a symplectic homeomorphism and also that it cannot be invariant by a symplectic twist diffeomorphism.
$C^1$
, we deduce from Theorems 1.1 and 1.3 that this foliation cannot be globally straightenable by a symplectic homeomorphism and also that it cannot be invariant by a symplectic twist diffeomorphism.
Proof of Corollary 1.3
We now work in
![]() $\mathbb {R}^2$
and assume by contradiction that there are two open sets
$\mathbb {R}^2$
and assume by contradiction that there are two open sets
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() ${\mathcal V}$
as in Theorem 1.3, and a symplectic homeomorphism
${\mathcal V}$
as in Theorem 1.3, and a symplectic homeomorphism
![]() $\Phi : {\mathcal U} \to {\mathcal V}$
that maps the horizontal lines of
$\Phi : {\mathcal U} \to {\mathcal V}$
that maps the horizontal lines of
![]() ${\mathcal U}$
to the leaves of the foliation in
${\mathcal U}$
to the leaves of the foliation in
![]() ${\mathcal V}$
preserving the orientation of the leaves. Let us denote
${\mathcal V}$
preserving the orientation of the leaves. Let us denote
![]() $(c_-,c_+) = \pi _2 ({\mathcal U})$
and
$(c_-,c_+) = \pi _2 ({\mathcal U})$
and
![]() $J\subset \mathbb {R}$
such that
$J\subset \mathbb {R}$
such that
![]() ${\mathcal V} =\{ (\theta , \eta _c(\theta )), \ \theta \in (\alpha ,\beta ), c\in J\} $
. By hypothesis, there exists an increasing homeomorphism
${\mathcal V} =\{ (\theta , \eta _c(\theta )), \ \theta \in (\alpha ,\beta ), c\in J\} $
. By hypothesis, there exists an increasing homeomorphism
![]() ${\mathfrak h : (c_-,c_+ ) \to J}$
such that if
${\mathfrak h : (c_-,c_+ ) \to J}$
such that if
![]() $c\in (c_-,c_+)$
, the horizontal line
$c\in (c_-,c_+)$
, the horizontal line
![]() $\mathbb {R}\times \{c\} \cap {\mathcal U}$
is mapped to the leaf of the foliation
$\mathbb {R}\times \{c\} \cap {\mathcal U}$
is mapped to the leaf of the foliation
![]() $\{ (\theta , \eta _{\mathfrak h(c)}(\theta )), \ \theta \in (\alpha ,\beta )\}$
by
$\{ (\theta , \eta _{\mathfrak h(c)}(\theta )), \ \theta \in (\alpha ,\beta )\}$
by
![]() $\Phi $
.
$\Phi $
.
Returning to the generating function, if
![]() $c\in (c_-,c_+)$
we have
$c\in (c_-,c_+)$
we have
![]() $u(0,c)=0$
and
$u(0,c)=0$
and
![]() $c+ ({\partial u}/{\partial \theta })(c,\theta ) = \eta _{\mathfrak h(c)}(\theta )$
from which we deduce that
$c+ ({\partial u}/{\partial \theta })(c,\theta ) = \eta _{\mathfrak h(c)}(\theta )$
from which we deduce that
Now let
![]() $\theta _1,\theta _2 \in (\alpha ,\beta )$
such that the matrix
$\theta _1,\theta _2 \in (\alpha ,\beta )$
such that the matrix
 $$ \begin{align*}A=\begin{pmatrix} \theta_1 & {\sin(2\pi \theta_1)}/{2\pi} \\ \theta_2 & {\sin(2\pi \theta_2)}/{2\pi} \end{pmatrix}\end{align*} $$
$$ \begin{align*}A=\begin{pmatrix} \theta_1 & {\sin(2\pi \theta_1)}/{2\pi} \\ \theta_2 & {\sin(2\pi \theta_2)}/{2\pi} \end{pmatrix}\end{align*} $$
is invertible. It follows that
 $$ \begin{align*}\text{for all } c\in (c_-,c_+), \quad \begin{pmatrix} \mathfrak h(c) \\ \varepsilon\circ \mathfrak h(c) \end{pmatrix} = A^{-1} \begin{pmatrix} u(\theta_1,c)+\theta_1c \\u(\theta_2,c)+\theta_2c \end{pmatrix}. \end{align*} $$
$$ \begin{align*}\text{for all } c\in (c_-,c_+), \quad \begin{pmatrix} \mathfrak h(c) \\ \varepsilon\circ \mathfrak h(c) \end{pmatrix} = A^{-1} \begin{pmatrix} u(\theta_1,c)+\theta_1c \\u(\theta_2,c)+\theta_2c \end{pmatrix}. \end{align*} $$
As by Theorem 1.3 the function u is
![]() $C^1$
, we deduce that
$C^1$
, we deduce that
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\varepsilon \circ \mathfrak h$
are
$\varepsilon \circ \mathfrak h$
are
![]() $C^1$
functions. It follows that
$C^1$
functions. It follows that
![]() $\mathfrak h'$
must vanish at all points c such that
$\mathfrak h'$
must vanish at all points c such that
![]() $\varepsilon $
is not differentiable at
$\varepsilon $
is not differentiable at
![]() $h(c)$
. As such points are dense, we conclude that
$h(c)$
. As such points are dense, we conclude that
![]() $\mathfrak h$
is constant which contradicts it being a homeomorphism onto its image.
$\mathfrak h$
is constant which contradicts it being a homeomorphism onto its image.
7.2 An exact symplectic twist map that leaves the strange foliation invariant
Let us prove, however, that this foliation, for a simple choice of
![]() $\varepsilon $
, can be invariant by a certain
$\varepsilon $
, can be invariant by a certain
![]() $C^1$
exact symplectic (weakly) twist map as defined below.
$C^1$
exact symplectic (weakly) twist map as defined below.
Definition. An exact symplectic homeomorphism
![]() $f:\mathbb {A}\rightarrow \mathbb {A}$
has the weak twist property if when
$f:\mathbb {A}\rightarrow \mathbb {A}$
has the weak twist property if when
![]() $F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f, for any
$F=(F_1, F_2):\mathbb {R}^2\rightarrow \mathbb {R}^2$
is any lift of f, for any
![]() $\tilde \theta \in \mathbb {R}$
, the map
$\tilde \theta \in \mathbb {R}$
, the map
![]() $r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing homeomorphism from
$r\in \mathbb {R}\mapsto F_1(\tilde \theta , r)\in \mathbb {R}$
is an increasing homeomorphism from
![]() $\mathbb {R}$
onto
$\mathbb {R}$
onto
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Let us now assume that
![]() $\varepsilon $
is a
$\varepsilon $
is a
![]() $C^2$
function away from
$C^2$
function away from
![]() $c=0$
and that at
$c=0$
and that at
![]() $0$
it has left and right derivatives up to order
$0$
it has left and right derivatives up to order
![]() $2$
. For the sake of simplicity, let us assume also that
$2$
. For the sake of simplicity, let us assume also that
![]() $\varepsilon (0)=0$
so that
$\varepsilon (0)=0$
so that
![]() $\mathbb {T}\times \{0\}$
is a leaf of the foliation and that
$\mathbb {T}\times \{0\}$
is a leaf of the foliation and that
![]() $\varepsilon $
restricted to
$\varepsilon $
restricted to
![]() $[0,+\infty )$
(respectively,
$[0,+\infty )$
(respectively,
![]() $(-\infty , 0]$
) is the restriction of a
$(-\infty , 0]$
) is the restriction of a
![]() $C^2$
periodic function.
$C^2$
periodic function.
The proof of Theorem 1.4 gives us two
![]() $C^1$
functions
$C^1$
functions
where
![]() $\Phi ^+$
is a
$\Phi ^+$
is a
![]() $C^1$
exact symplectic diffeomorphism of
$C^1$
exact symplectic diffeomorphism of
![]() $\mathbb {A}^+ = \mathbb {T} \times [0,+\infty )$
to itself (up to the boundary) and
$\mathbb {A}^+ = \mathbb {T} \times [0,+\infty )$
to itself (up to the boundary) and
![]() $\Phi _-$
is a
$\Phi _-$
is a
![]() $C^1$
exact symplectic diffeomorphism of
$C^1$
exact symplectic diffeomorphism of
![]() $\mathbb {A}^- = \mathbb {T} \times (-\infty , 0]$
to itself (up to the boundary). Note that here
$\mathbb {A}^- = \mathbb {T} \times (-\infty , 0]$
to itself (up to the boundary). Note that here
![]() $\Phi ^+$
and
$\Phi ^+$
and
![]() $\Phi ^-$
do not coincide on
$\Phi ^-$
do not coincide on
![]() $\mathbb {T}\times \{0\}$
. explaining why the foliation is not straightenable.
$\mathbb {T}\times \{0\}$
. explaining why the foliation is not straightenable.
Let
![]() $\rho : \mathbb {R} \to \mathbb {R}$
be an increasing,
$\rho : \mathbb {R} \to \mathbb {R}$
be an increasing,
![]() $C^1$
homeomorphism such that
$C^1$
homeomorphism such that
![]() $\rho (0) = \rho '(0) = 0$
. We denote
$\rho (0) = \rho '(0) = 0$
. We denote
![]() $f_\rho : (\theta ,r) \mapsto (\theta +\rho (r) , r)$
. The function
$f_\rho : (\theta ,r) \mapsto (\theta +\rho (r) , r)$
. The function
![]() $f = \Phi ^\pm \circ f_\rho \circ (\Phi ^\pm )^{-1}$
is well defined on
$f = \Phi ^\pm \circ f_\rho \circ (\Phi ^\pm )^{-1}$
is well defined on
![]() $\mathbb {A}$
; it is the identity on
$\mathbb {A}$
; it is the identity on
![]() $\mathbb {T} \times \{0\}$
. It is clearly an area-preserving homeomorphism that is
$\mathbb {T} \times \{0\}$
. It is clearly an area-preserving homeomorphism that is
![]() $C^1$
away from
$C^1$
away from
![]() $\mathbb {T}\times \{0\}$
.
$\mathbb {T}\times \{0\}$
.
If
![]() $r> 0$
and
$r> 0$
and
![]() $\theta \in \mathbb {T}$
, let us set
$\theta \in \mathbb {T}$
, let us set
![]() $(\Theta ,R) = \Phi ^+(\theta ,r) $
. Then one finds that
$(\Theta ,R) = \Phi ^+(\theta ,r) $
. Then one finds that
 $$ \begin{align*} D f(\Theta,R) &= D\Phi^+(\theta + \rho(r),r) \cdot Df_\rho ( \theta,r)\cdot D\Phi^+(\theta,r)^{-1} \\ &= D\Phi^+(\theta + \rho(r),r) \cdot \begin{pmatrix}1&\rho'(r)\\0&1 \end{pmatrix} \cdot D\Phi^+(\theta,r)^{-1}. \end{align*} $$
$$ \begin{align*} D f(\Theta,R) &= D\Phi^+(\theta + \rho(r),r) \cdot Df_\rho ( \theta,r)\cdot D\Phi^+(\theta,r)^{-1} \\ &= D\Phi^+(\theta + \rho(r),r) \cdot \begin{pmatrix}1&\rho'(r)\\0&1 \end{pmatrix} \cdot D\Phi^+(\theta,r)^{-1}. \end{align*} $$
It follows from the properties on
![]() $\Phi ^+$
and
$\Phi ^+$
and
![]() $\rho (0)=\rho '(0) = 0$
that as
$\rho (0)=\rho '(0) = 0$
that as
![]() $R\to 0$
,
$R\to 0$
,
![]() $Df(\Theta ,R)$
uniformly converges to the identity. As the same holds for
$Df(\Theta ,R)$
uniformly converges to the identity. As the same holds for
![]() $R<0$
, we deduce that f is in fact
$R<0$
, we deduce that f is in fact
![]() $C^1$
with a differential on
$C^1$
with a differential on
![]() $\mathbb {T} \times \{0\}$
being identity.
$\mathbb {T} \times \{0\}$
being identity.
It remains to choose
![]() $\rho $
in such a way that the map obtained is a twist map. We construct it on
$\rho $
in such a way that the map obtained is a twist map. We construct it on
![]() $[0,+\infty )$
. The twist condition we aim at is: for every
$[0,+\infty )$
. The twist condition we aim at is: for every
![]() $\Theta \in \mathbb {R}$
, the map
$\Theta \in \mathbb {R}$
, the map
![]() $r\mapsto h^+((h^{+}_r)^{-1}(\Theta )+\rho (r),r)$
is an increasing homeomorphism of
$r\mapsto h^+((h^{+}_r)^{-1}(\Theta )+\rho (r),r)$
is an increasing homeomorphism of
![]() $\mathbb {R}$
where
$\mathbb {R}$
where
![]() $h^+_r = h^+(\cdot ,r)$
.
$h^+_r = h^+(\cdot ,r)$
.
After computation, if we denote
![]() $h^+(\theta _r, r)=\Theta $
, the derivative of the above function is the following for
$h^+(\theta _r, r)=\Theta $
, the derivative of the above function is the following for
![]() $r>0$
(the inequality is our goal):
$r>0$
(the inequality is our goal):
 $$ \begin{align*} &\frac{\partial h^+}{\partial r}(\theta_r+\rho(r),r)-\bigg( \frac{\partial h^+}{\partial \theta}(\theta_r,r)\bigg)^{-1}\frac{\partial h^+}{\partial \theta}(\theta_r+\rho(r),r)\frac{\partial h^+}{\partial r}(\theta_r,r) \\ &\quad+ \frac{\partial h^+}{\partial \theta}(\theta_r+\rho(r),r)\rho'(r)>0. \end{align*} $$
$$ \begin{align*} &\frac{\partial h^+}{\partial r}(\theta_r+\rho(r),r)-\bigg( \frac{\partial h^+}{\partial \theta}(\theta_r,r)\bigg)^{-1}\frac{\partial h^+}{\partial \theta}(\theta_r+\rho(r),r)\frac{\partial h^+}{\partial r}(\theta_r,r) \\ &\quad+ \frac{\partial h^+}{\partial \theta}(\theta_r+\rho(r),r)\rho'(r)>0. \end{align*} $$
The first line above is smaller in absolute value than
![]() $M_1\rho (r)$
where (recall that by hypothesis, all the functions at play are continuous periodic, hence bounded)
$M_1\rho (r)$
where (recall that by hypothesis, all the functions at play are continuous periodic, hence bounded)
 $$ \begin{align*}M_1 = \bigg \|\frac{\partial^2 h^+}{\partial r\partial \theta}\bigg \|_\infty +\bigg \|\bigg(\frac{\partial h^+}{\partial \theta}\bigg)^{-1}\bigg \|_\infty. \bigg \|\frac{\partial^2 h^+}{\partial \theta^2}\bigg \|_\infty \bigg \|\frac{\partial h^+}{\partial r}\bigg \|_\infty .\end{align*} $$
$$ \begin{align*}M_1 = \bigg \|\frac{\partial^2 h^+}{\partial r\partial \theta}\bigg \|_\infty +\bigg \|\bigg(\frac{\partial h^+}{\partial \theta}\bigg)^{-1}\bigg \|_\infty. \bigg \|\frac{\partial^2 h^+}{\partial \theta^2}\bigg \|_\infty \bigg \|\frac{\partial h^+}{\partial r}\bigg \|_\infty .\end{align*} $$
On the other hand, the second line is greater than
![]() $M_2 \rho '(r)$
, where we set
$M_2 \rho '(r)$
, where we set
![]() $ M_2 = \min ({\partial h^+}/{\partial \theta })>0$
. If
$ M_2 = \min ({\partial h^+}/{\partial \theta })>0$
. If
![]() $\rho (t) = t^2 e^{Mt}$
with
$\rho (t) = t^2 e^{Mt}$
with
![]() $M= 2M_1/M_2$
, then we have
$M= 2M_1/M_2$
, then we have
![]() $\rho (0)=\rho '(0)=0$
and
$\rho (0)=\rho '(0)=0$
and
![]() $\rho '(t)>({M_1}/{M_2})\rho (t)$
which implies the twist condition.
$\rho '(t)>({M_1}/{M_2})\rho (t)$
which implies the twist condition.
Acknowledgements
The authors are grateful to Philippe Bolle for insightful discussions that helped clarify and simplify some proofs in this work. They thank Sobhan Seyfaddini for his insight on symplectic homeomorphisms. The authors thank the anonymous referees. Their careful reading helped to remove some unclear formulations and misleading notation. M. Zavidovique was financed by a bursary PEPS from CNRS.
A Appendix. Foliation by graphs that is the inverse image of the standard foliation by a symplectic map but not by a symplectic homeomorphism
We will use two special functions:
-
•
 $\gamma :\mathbb {T}\rightarrow \mathbb {R}$
, a
$\gamma :\mathbb {T}\rightarrow \mathbb {R}$
, a
 $C^\infty $
function such that
$C^\infty $
function such that
 $\gamma ^{\prime }_{[1/2 - \varepsilon , 1/2 + \varepsilon ]}=-1$
and
$\gamma ^{\prime }_{[1/2 - \varepsilon , 1/2 + \varepsilon ]}=-1$
and
 $\gamma ^{\prime }_{\mathbb {T}\backslash [1/2-\varepsilon , 1/2+\varepsilon ]}>-1$
;
$\gamma ^{\prime }_{\mathbb {T}\backslash [1/2-\varepsilon , 1/2+\varepsilon ]}>-1$
; -
•
 $\zeta :\mathbb {R}\rightarrow \mathbb {R}$
, a
$\zeta :\mathbb {R}\rightarrow \mathbb {R}$
, a
 $C^\infty $
function that is increasing, such that
$C^\infty $
function that is increasing, such that
 $\zeta '(0)=1$
and
$\zeta '(0)=1$
and
 $\zeta ^{\prime }_{\mathbb {R}\backslash \{ 0\}}<1$
with
$\zeta ^{\prime }_{\mathbb {R}\backslash \{ 0\}}<1$
with
 ${\lim _{\pm \infty }\zeta '=\tfrac 12}$
.
${\lim _{\pm \infty }\zeta '=\tfrac 12}$
.
The function
![]() $u(\theta , c)=\zeta (c)\gamma (\theta )$
defines the foliation in graphs of
$u(\theta , c)=\zeta (c)\gamma (\theta )$
defines the foliation in graphs of
The derivative with respect to c of
![]() $\eta _c(\theta )$
is then
$\eta _c(\theta )$
is then
![]() $({\partial \eta _c}/{\partial c})(\theta )=1+\zeta '(c)\gamma '(\theta )$
which is non-negative, vanishes only for
$({\partial \eta _c}/{\partial c})(\theta )=1+\zeta '(c)\gamma '(\theta )$
which is non-negative, vanishes only for
![]() $(\theta , c)\in [\tfrac 12-\varepsilon , \tfrac 12+\varepsilon ]\times \{0\}$
and is greater that
$(\theta , c)\in [\tfrac 12-\varepsilon , \tfrac 12+\varepsilon ]\times \{0\}$
and is greater that
![]() $\tfrac 13$
close to
$\tfrac 13$
close to
![]() $\pm \infty $
. Hence every map
$\pm \infty $
. Hence every map
![]() $c\in \mathbb {R}\mapsto \eta _c(\theta )\in \mathbb {R}$
is a homeomorphism and we indeed have a
$c\in \mathbb {R}\mapsto \eta _c(\theta )\in \mathbb {R}$
is a homeomorphism and we indeed have a
![]() $C^0$
foliation.
$C^0$
foliation.
Let us introduce
![]() $h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta )=\theta +\gamma (\theta )\zeta '(c)$
. Its derivative is
$h_c(\theta )=\theta +({\partial u}/{\partial c})(\theta )=\theta +\gamma (\theta )\zeta '(c)$
. Its derivative is
![]() $1+\zeta '(c)\gamma '(\theta )$
that is non negative and vanishes only if
$1+\zeta '(c)\gamma '(\theta )$
that is non negative and vanishes only if
![]() $(\theta , c)\in [\tfrac 12-\varepsilon , \tfrac 12+\varepsilon ]\times \{0\}$
. Hence
$(\theta , c)\in [\tfrac 12-\varepsilon , \tfrac 12+\varepsilon ]\times \{0\}$
. Hence
![]() $h_0$
is not a homeomorphism but all the other
$h_0$
is not a homeomorphism but all the other
![]() $h_c$
are homeomorphisms.
$h_c$
are homeomorphisms.
We deduce from Theorem 1.3 that this foliation is not symplectically homeomorphic to the standard one.
We will now prove that the map defined by
![]() $H(\theta , \eta _c(\theta ))=(h_c(\theta ), c)$
is a symplectic map, the limit (for the
$H(\theta , \eta _c(\theta ))=(h_c(\theta ), c)$
is a symplectic map, the limit (for the
![]() $C^0$
topology) of a sequence of symplectic diffeomorphisms.
$C^0$
topology) of a sequence of symplectic diffeomorphisms.
Let
![]() $\gamma _n:\mathbb {T}\rightarrow \mathbb {R}$
be a sequence of
$\gamma _n:\mathbb {T}\rightarrow \mathbb {R}$
be a sequence of
![]() $C^\infty $
maps that converges to
$C^\infty $
maps that converges to
![]() $\gamma $
in
$\gamma $
in
![]() $C^1$
topology and satisfies
$C^1$
topology and satisfies
![]() $\gamma _n'>-1$
. Let
$\gamma _n'>-1$
. Let
![]() $(\zeta _n)$
be a sequence of
$(\zeta _n)$
be a sequence of
![]() $C^\infty $
diffeomorphisms of
$C^\infty $
diffeomorphisms of
![]() $\mathbb {R}$
that
$\mathbb {R}$
that
![]() $C^1$
converges to
$C^1$
converges to
![]() $\zeta $
and satisfies
$\zeta $
and satisfies
![]() $\zeta _n'<1$
. We introduce
$\zeta _n'<1$
. We introduce
![]() $u_n(\theta , c)=\gamma _n(\theta )\zeta _n(c)$
. Then
$u_n(\theta , c)=\gamma _n(\theta )\zeta _n(c)$
. Then
![]() $\eta _{c,n}(\theta )=c+\zeta _n(c)\gamma _n'(\theta )$
defines a smooth foliation,
$\eta _{c,n}(\theta )=c+\zeta _n(c)\gamma _n'(\theta )$
defines a smooth foliation,
![]() $h_{c,n}(\theta )=\theta +\gamma _n(\theta )\zeta _n'(c)$
is a smooth diffeomorphism of
$h_{c,n}(\theta )=\theta +\gamma _n(\theta )\zeta _n'(c)$
is a smooth diffeomorphism of
![]() $\mathbb {T}$
and
$\mathbb {T}$
and
is a symplectic smooth diffeomorphism that maps the standard foliation to the foliations by the graphs of
![]() $( \eta _{c,n})_{c\in \mathbb {R}}$
.
$( \eta _{c,n})_{c\in \mathbb {R}}$
.
If
![]() $H_n=K_n^{-1}$
, observe that
$H_n=K_n^{-1}$
, observe that
![]() $H_n=G_n\circ F_n^{-1}$
where:
$H_n=G_n\circ F_n^{-1}$
where:
-
•
 $F_n(\theta , c)=(\theta , c+({\partial u_n}/{\partial \theta })(\theta , c))$
converges uniformly to
$F_n(\theta , c)=(\theta , c+({\partial u_n}/{\partial \theta })(\theta , c))$
converges uniformly to
 $F(\theta , c)=(\theta , c+({\partial u}/{\partial \theta }) (\theta , c))$
;
$F(\theta , c)=(\theta , c+({\partial u}/{\partial \theta }) (\theta , c))$
; -
•
 $G_n(\theta , c)=(\theta +({\partial u_n}/{\partial c})(\theta , c), c)$
converges uniformly to
$G_n(\theta , c)=(\theta +({\partial u_n}/{\partial c})(\theta , c), c)$
converges uniformly to
 $G(\theta , c)=(\theta + ({\partial u}/{\partial c}) (\theta , c), c)$
.
$G(\theta , c)=(\theta + ({\partial u}/{\partial c}) (\theta , c), c)$
.
Finally,
![]() $H_n=G_n\circ F_n^{-1}$
converges uniformly to
$H_n=G_n\circ F_n^{-1}$
converges uniformly to
![]() $H=G\circ F^{-1}$
.
$H=G\circ F^{-1}$
.
B Appendix. Green bundles
Here we recall the theory of Green bundles. More details and proofs can be found in [Reference Arnaud1, Reference Arnaud2]. We fix a lift F of a symplectic twist diffeomorphism f.
Notation.
-
•
 $V(x)=\{ 0\}\times \mathbb {R}\subset T_x\mathbb {R}^2$
, and for
$V(x)=\{ 0\}\times \mathbb {R}\subset T_x\mathbb {R}^2$
, and for
 $k\not = 0$
we set
$k\not = 0$
we set
 $G_k(x)=DF^k(F^{-k}x)V(f^{-k}x)$
.
$G_k(x)=DF^k(F^{-k}x)V(f^{-k}x)$
. -
• The slope of
 $G_k$
(when defined) is denoted by
$G_k$
(when defined) is denoted by
 $s_k$
:
$s_k$
:  $$ \begin{align*}G_k(x)=\{ (\delta\theta, s_k(x)\delta\theta);\ \delta\theta\in\mathbb{R}\}.\end{align*} $$
$$ \begin{align*}G_k(x)=\{ (\delta\theta, s_k(x)\delta\theta);\ \delta\theta\in\mathbb{R}\}.\end{align*} $$
-
• If
 $\gamma $
is a real Lipschitz function defined on
$\gamma $
is a real Lipschitz function defined on
 $\mathbb {T}$
or
$\mathbb {T}$
or
 $\mathbb {R}$
, then
$\mathbb {R}$
, then  $$ \begin{align*}\gamma^{\prime}_+(x)=\limsup_{\substack{y,z\rightarrow x\\ y\not=z}}\frac{\gamma(y)-\gamma(z)}{y-z}\quad\textrm{and}\quad \gamma^{\prime}_-(t)=\liminf_{\substack{y,z\rightarrow x\\ y\not=z}}\frac{\gamma(y)-\gamma(z)}{y-z}.\end{align*} $$
$$ \begin{align*}\gamma^{\prime}_+(x)=\limsup_{\substack{y,z\rightarrow x\\ y\not=z}}\frac{\gamma(y)-\gamma(z)}{y-z}\quad\textrm{and}\quad \gamma^{\prime}_-(t)=\liminf_{\substack{y,z\rightarrow x\\ y\not=z}}\frac{\gamma(y)-\gamma(z)}{y-z}.\end{align*} $$
Then:
-
(1) if the orbit of
 $x\in \mathbb {R}^2$
is minimizing (see [Reference Arnaud1, Reference Arnaud2] for the definition; the only thing needed here is that an orbit that is contained in an invariant curve that is a graph is minimizing), we have
$x\in \mathbb {R}^2$
is minimizing (see [Reference Arnaud1, Reference Arnaud2] for the definition; the only thing needed here is that an orbit that is contained in an invariant curve that is a graph is minimizing), we have  $$ \begin{align*}\text{for all } n\geq 1,\quad s_{-n}(x)<s_{-n-1}(x)<s_{n+1}(x)<s_n(x);\end{align*} $$
$$ \begin{align*}\text{for all } n\geq 1,\quad s_{-n}(x)<s_{-n-1}(x)<s_{n+1}(x)<s_n(x);\end{align*} $$
-
(2) in this case, the two Green bundles at x are
 $G_+(x), G_-(x)\subset T_x(\mathbb {R}^2)$
with slopes
$G_+(x), G_-(x)\subset T_x(\mathbb {R}^2)$
with slopes
 $s_-$
,
$s_-$
,
 $s_+$
where
$s_+$
where
 ${s_+(x)=\lim _{n\rightarrow +\infty }s_n(x)}$
and
${s_+(x)=\lim _{n\rightarrow +\infty }s_n(x)}$
and
 ${ s_-(x)=\lim _{n\rightarrow +\infty }s_{-n}(x)}$
;
${ s_-(x)=\lim _{n\rightarrow +\infty }s_{-n}(x)}$
; -
(3) the two Green bundles are invariant under
 $Df$
:
$Df$
:
 $Df(G_\pm )=G_\pm \circ f$
;
$Df(G_\pm )=G_\pm \circ f$
; -
(4) we have
 $s_+\geq s_-$
;
$s_+\geq s_-$
; -
(5) the map
 $s_-$
is lower semi-continuous and the map
$s_-$
is lower semi-continuous and the map
 $s_+$
is upper semi-continuous;
$s_+$
is upper semi-continuous; -
(6) hence
 $\{ G_-=G_+\}$
is a
$\{ G_-=G_+\}$
is a
 $G_\delta $
subset of the set of points whose orbit is minimizing (this last set is a closed set) and
$G_\delta $
subset of the set of points whose orbit is minimizing (this last set is a closed set) and
 $s_-=s_+$
is continuous at every point of this set.
$s_-=s_+$
is continuous at every point of this set.
Let us focus on the case of an invariant curve that is the graph of
![]() $\gamma :\mathbb {T}\rightarrow \mathbb {R}$
. Then we have the following propositions.
$\gamma :\mathbb {T}\rightarrow \mathbb {R}$
. Then we have the following propositions.
Proposition B.1. Assume that the graph of a function
![]() $\gamma \in C^0(\mathbb {T}, \mathbb {R})$
is invariant by F. Then the orbit of any point contained in the graph of
$\gamma \in C^0(\mathbb {T}, \mathbb {R})$
is invariant by F. Then the orbit of any point contained in the graph of
![]() $\gamma $
is minimizing and we have
$\gamma $
is minimizing and we have
Proposition B.2. (Dynamical criterion)
Assume that x has its orbit that is minimizing and that is contained in some strip
![]() $\mathbb {R}\times [-K,K]$
(for example, x is in some invariant graph) and that
$\mathbb {R}\times [-K,K]$
(for example, x is in some invariant graph) and that
![]() $v\in T_x\mathbb {R}^2\backslash \{ 0\}$
. Then:
$v\in T_x\mathbb {R}^2\backslash \{ 0\}$
. Then:
-
• if
 ${\liminf _{n\rightarrow +\infty } \lvert D(\pi \circ F^n)(x)v\rvert <+\infty }$
, then
${\liminf _{n\rightarrow +\infty } \lvert D(\pi \circ F^n)(x)v\rvert <+\infty }$
, then
 $v\in G_-(x)$
;
$v\in G_-(x)$
; -
• if
 ${\liminf _{n\rightarrow +\infty } \lvert D(\pi \circ F^{-n})(x)v\rvert <+\infty }$
, then
${\liminf _{n\rightarrow +\infty } \lvert D(\pi \circ F^{-n})(x)v\rvert <+\infty }$
, then
 $v\in G_+(x)$
.
$v\in G_+(x)$
.
In particular, if the dynamics restricted to some invariant graph is totally periodic, then along this graph we have
![]() $G_-=G_+$
and the graph is
$G_-=G_+$
and the graph is
![]() $C^1$
. The
$C^1$
. The
![]() $C^1$
property can also be proved by using the implicit functions theorem.
$C^1$
property can also be proved by using the implicit functions theorem.