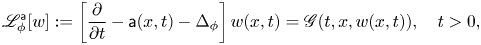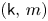Differential Harnack estimates for a weighted nonlinear parabolic equation under a super Perelman–Ricci flow and implications

Abstract

In this paper, we derive new differential Harnack estimates of Li–Yau type for positive smooth solutions to a class of nonlinear parabolic equations in the form

\[ {\mathscr L}_\phi^{\mathsf a} [w]:= \left[ \frac{\partial}{\partial t} - \mathsf{a}(x,t) - \Delta_\phi \right] w (x,t) = \mathscr G(t, x, w(x,t)), \quad t>0, \]

on smooth metric measure spaces where the metric and potential are time dependent and evolve under a $({\mathsf k},\, m)$-super Perelman–Ricci flow. A number of consequences, most notably, a parabolic Harnack inequality, a class of Hamilton type global curvature-free estimates and a general Liouville type theorem together with some consequences are established. Some special cases are presented to illustrate the strength of the results.

1. Introduction

In this paper, we study gradient estimates for positive smooth solutions to a class of nonlinear parabolic equations on smooth metric measure spaces with evolving geometry. Whilst gradient estimates have been studied over the years for linear and nonlinear equations on static manifolds or for equations of mainly Schrödinger and heat types on evolving manifolds, the investigation of nonlinear parabolic equations on smooth metric measure spaces with evolving metrics and potentials is relatively new and recent. These problems pose interesting challenges and technicalities whilst having huge scope for applications as already known and further discussed below.

To this end let $(M,\,g)$ be a complete (smooth) Riemannian manifold of dimension $n \ge 2$ with Riemannain volume measure ${\rm d}v_g$ and let ${\rm d}\sigma = \omega {\rm d}v_g$ be a positive weighted measure on $M$ with weight function $\omega > 0$ and potential $\phi =-\log \omega$. The triple $(M,\, g,\, {\rm d}\sigma )$ is called a smooth metric measure space or a weighted manifold or a manifold with density (see [8, 21] for background and § 3).

Our aim here is to prove differential Harnack estimates for positive smooth solutions $w=w(x,\,t)$ to the following nonlinear parabolic equation on $(M,\,g,\,{\rm d}\sigma )$ where the metric tensor $g$ and potential $\phi$ evolve under a $(\mathsf {k},\,m)$-super Perelman–Ricci flow:

(1.1)\begin{equation} \begin{cases} \mathscr L^{\mathsf a}_\phi [w] (x,t) = \left[ \dfrac{\partial}{\partial t} - \mathsf{a} (x,t) - \Delta_\phi \right] w (x,t) = \mathscr G(t, x, w(x,t)), \quad t>0, \\ \dfrac{1}{2} \dfrac{\partial g}{\partial t} (x,t) + {\mathscr Ric}^m_\phi(g)(x,t) \ge - \mathsf{k}g(x,t), \qquad m \ge n, {\mathsf k} \ge 0, \\ {\mathscr Ric}^m_\phi(g)(x,t) = {\mathscr Ric} (g)(x,t) + \nabla_{g(t)} \nabla_{g(t)} \phi (x,t) - \dfrac{\nabla_{g(t)} \phi \otimes \nabla_{g(t)} \phi}{m-n}. \end{cases} \end{equation}

To describe the above system in more detail we first note that the differential operator $\Delta _\phi$ in (1.1) is the $\phi$-Laplacian associated with the triple $(M,\,g,\,d\sigma )$ (also known as the weighted or drifting or Witten Laplacian). It is a natural extension of the Riemannian Laplacian to the smooth metric measure space setting whose action on $v \in \mathscr {C}^2(M)$ can be described by

(1.2)\begin{equation} \Delta_\phi v = \Delta v - \langle \nabla \phi, \nabla v \rangle = {\rm e}^\phi {\rm div} ({\rm e}^{-\phi} \nabla v). \end{equation}

Here, $\Delta,\, {\rm div}$ and $\nabla$ are the usual Laplace–Beltrami, divergence and gradient operators associated with the metric tensor $g$ respectively. Naturally, when the metric tensor $g$ and potential $\phi$ are time dependent this (spatial) differential operator is time dependent too (in that its coefficients depend explicitly on the time variable). Continuing further and referring again to the first equation in (1.1), the time evolution operators

(1.3)\begin{equation} {\mathscr L}_\phi^{\mathsf a} = \frac{\partial}{\partial t} - {\mathsf a}(x,t) - \Delta_\phi, \quad \mathscr L_\phi = {\mathscr L}^0_\phi = \frac{\partial}{\partial t} - \Delta_\phi, \quad {\mathscr L}_\phi^{\mathsf a} = {\mathscr L}_\phi - {\mathsf a}, \end{equation}

are the ${\mathsf a}$-weighted (and weighted) heat operators with $\mathsf a=\mathsf a(x,\,t)$ a sufficiently smooth function of the space–time variables $(x,\,t)$. The nonlinearity $\mathscr G=\mathscr G(t,\,x,\,w)$ on the right-hand side here is a sufficiently smooth function depending on both the space–time variables and the dependent variable $w$. We shall present later on, various examples of such nonlinearities from different contexts ranging from conformal geometry, relativity and mathematical physics to applications of mathematics in materials and biological sciences, each representing a different phenomenon whilst depicting a corresponding singular or regular behaviour on its domain.

The differential inequality and equation on the second and third lines in system (1.1) respectively describe the evolution of the geometry of the triple $(M,\,g,\,d\sigma )$. Indeed the inequality in the second line in (1.1) describes the evolution of the generalized Ricci curvature tensor that in turn should be interpreted in the sense of symmetric $(2,\,0)$ tensors whilst the equation on the third line gives the formulation of this generalized Ricci tensor that in turn involves the usual Ricci curvature tensor associated with $g$, the Hessian of $\phi$ and a rank-one symmetric tensor involving the gradient of $\phi$ (see § 3 for more on notation and background). Here $m \ge n$ is a constant (not necessarily an integer) having the role of a dimension and ${\mathsf k} \ge 0$ is a fixed constant.

It is evident that the static case, that is, the case with time-independent metrics and potentials, constitutes a special case of system (1.1). In this event, the differential inequality on the second line in the system reduces to a spatial lower bound on the (time independent) generalized Ricci tensor (see § 3 for more), that is,

(1.4)\begin{equation} {\mathscr Ric}_\phi^m(g) = {\mathscr Ric} (g) + \nabla \nabla \phi - \frac{\nabla \phi \otimes \nabla \phi}{m-n} \ge -{\mathsf k} g.\end{equation}

Here gradient estimates for positive solutions to linear and nonlinear heat type equations have been studied extensively starting from the seminal paper of Li and Yau [29] (see also [28]). In the nonlinear setting perhaps the first equation to be considered is the one with a logarithmic type nonlinearity (see e.g., [27, 33, 52])

(1.5)\begin{equation} {\mathscr L}_\phi^{\mathsf a} [w] = \left[\frac{\partial}{\partial t} - \mathsf a(x,t) - \Delta_\phi \right] w = {\mathsf A}(x,t) w \log w. \end{equation}

The interest in such problems originates partly from its natural links with gradient Ricci solitons and partly from links with geometric and functional inequalities on manifolds, notably, the logarithmic Sobolev and energy-entropy inequalities [7, 8, 22, 49]. Recall that a Riemannian manifold $(M,\,g)$ is said to be a gradient Ricci soliton if there exists a smooth function $\phi$ on $M$ and a constant $\lambda \in \mathbb {R}$ such that (cf. [13, 16, 32])

(1.6)\begin{equation} {\mathscr Ric}_\phi(g) = {\mathscr Ric}(g) + \nabla \nabla \phi = \lambda g. \end{equation}

The notion is a generalization of an Einstein manifold and has a fundamental role in the analysis of singularities of the Ricci flow [24, 55].

Another prominent class of nonlinear equations rooted in conformal geometry and studied extensively are the Yamabe type equations (see [9, 20, 26, 34]). In the context of smooth metric measure spaces these equations can be broadly studied as (see e.g., [17, 40, 41, 54])

(1.7)\begin{equation} {\mathscr L}_\phi [w] = \frac{\partial w}{\partial t} - \Delta_\phi w = {\mathsf A}(x,t) w^p + {\mathsf B}(x,t) w. \end{equation}

Incidentally, the case ${\mathsf A} \equiv -1$, ${\mathsf B} \equiv 1$, $p=3$ [${\mathscr G}(w) = w-w^3$] is the Allen–Cahn equation and the case ${\mathsf A} \equiv -c$, ${\mathsf B} \equiv c$, $p=2$ [${\mathscr G}(w)=cw(1-w)$ with $c>0$] is the Fisher-KKP equation (cf. [2, 18, 25]). Both these equations have been studied extensively in recent years due to the significance of the phenomenon they model and their huge applications in physics and other sciences (for various geometric estimates and their consequences, see [5, 14, 44] and the references therein). A far reaching generalization of (1.7) with a superposition of power-like nonlinearities consist of equations in the form

(1.8)\begin{equation} {\mathscr L}_\phi[w] = \frac{\partial w}{\partial t} - \Delta_\phi w = \sum_{j=1}^d {\mathsf A}_j(x,t) w^{p_j} + \sum_{j=1}^d {\mathsf B}_j(x,t) w^{q_j}. \end{equation}

Here ${\mathsf A}_j$, ${\mathsf B}_j$ (with $1 \le j \le d$) are sufficiently smooth space–time dependent coefficients and $p_j \ge 0$, $q_j \le 0$ real exponents (see [42, 43]). Other classes of equations generalizing the above and close to (1.5) come in the form (see e.g., [1, 10, 19, 42, 43, 48, 53])

(1.9)\begin{equation} {\mathscr L}^{\mathsf a}_\phi [w] = \left[\frac{\partial }{\partial t} - {\mathsf a} (x,t) - \Delta_\phi \right] w = {\mathsf A}(x,t) w^p \Phi(\log w) + {\mathsf B}(x,t) w^q, \end{equation}

with $p$, $q$ real exponents, ${\mathsf A}$, ${\mathsf B}$ sufficiently smooth coefficients and $\Phi \in {\mathscr C}^1(\mathbb {R},\, \mathbb {R})$. Some cases of interest for $\Phi =\Phi (s)$ include power function, e.g., $s^\alpha$ (integer $\alpha \ge 1$), $|s|^\alpha$ or $|s|^{\alpha -1} s$ (real $\alpha >1$) with different sign-changing, growth and singular behaviour as $\log w \to \pm \infty$ or a superposition of such nonlinearities [43]. Furthermore, the case of iterated logarithms as introduced in [10] with $d$, $k_1,\, \cdots,\, k_d \in {\mathbb {N}}$ and $\beta _1,\, \cdots,\, \beta _d \in {\mathbb {R}}$,

(1.10)\begin{equation} \Phi_{k_1, \dots, k_d}^{\beta_1, \dots, \beta_d} (\log w) = |\log_{k_1} w|^{\beta_1} |\log_{k_2} w|^{\beta_2} \dots |\log_{k_d} w|^{\beta_d}, \end{equation}

where $\log _k w = \log \log _{k-1} w$ for $k \ge 2$ and $\log _1 w = \log w$ can also be considered but only with due care, e.g., subject to the assumption of $w$ being sufficiently large, specifically, with respect to iterated exponentials of $k_1,\, \dots,\, k_d$ (as otherwise the repeated logarithm is meaningless due to the possibility of $\log _{k-1} w$ being non-positive hence making $\log _k w$ undefined).¹ Naturally, one can also consider variations of the same theme, e.g., by replacing $\log _k$ with either

(1.11)\begin{align} & \log^{||}_k w = \log^{||} \log^{||}_{k-1} w \text{ for }k \ge 2, \quad \log^{||}_1 w = |\log w|, \end{align}

(1.12)\begin{align} & \log^+_k w = \log^+ \log^+_{k-1} w \text{ for }k \ge 2, \quad \log^+_1 w = 1+ [\log w]_+. \end{align}

However, one needs to observe that the function $\Phi$ thus obtained is only ${\mathscr C}^1$ outside a discrete set (the zero sets of the functions $\log _{k-1} w$) and hence does not lie in ${\mathscr C}^1({\mathbb {R}},\, {\mathbb {R}})$ as required.

Another related and yet more general form of Yamabe type equations is the Einstein-scalar field Lichnerowicz equation (see Choquet-Bruhat [15], Chow [16] and Zhang [55]). In the context of smooth metric measure spaces a generalization of the Einstein-scalar field Lichnerowicz equation with space–time dependent coefficients can be described as:

(1.13)\begin{align} {\mathscr L}_\phi [w] & = \frac{\partial w}{\partial t} - \Delta_\phi w = {\mathsf A}(x,t) w^p + {\mathsf B}(x,t) w^q + {\mathsf C}(x,t) w \log w, \end{align}

(1.14)\begin{align} {\mathscr L}_\phi^{\mathsf a} [w] & = \left[ \frac{\partial }{\partial t} - {\mathsf a}(x,t) - \Delta_ \phi \right] w = {\mathsf A}(x,t) e^{2w} + {\mathsf B}(x,t) e^{{-}2w} + {\mathsf C}(x,t). \end{align}

For gradient estimates, Harnack inequalities, Liouville type theorems and other related results in this direction see [17, 31, 42, 43, 54] and the references therein.

Moving on to the evolving case the time dependence of the metric-potential pair adds further complications and technical details as far as gradient estimates are concerned. Here the case of the weighted heat equation under the Perelman–Ricci flow, generalizing in turn, the heat equation under the Ricci flow to the setting to smooth metric measure spaces, given by the system

(1.15)\begin{equation} \begin{cases} {\mathscr L}^{\mathsf a}_\phi [w](x,t) = \left[\dfrac{\partial}{\partial t} - {\mathsf a} (x,t) - \Delta_\phi\right] w(x,t) =0, \\ \dfrac{1}{2} \dfrac{\partial g}{\partial t}(x,t) + {\mathscr Ric}_\phi (g)(x,t) =0, \\ \end{cases} \end{equation}

has been considered by many authors (see, e.g., [4, 12, 16, 23, 30, 35, 36, 39, 47, 50, 55]).

System (1.1) can be seen as a generalization of (1.15) in two important ways. Firstly, the weighted linear heat equation is replaced by its nonlinear counterpart where the nonlinearity takes a considerably general formulation. Secondly, the Perelman–Ricci flow (with equality) is replaced by the $(\mathsf {k},\,m)$-super Perelman–Ricci flow (with inequality) which is equally a substantial and far reaching generalization (see [37, 38, 42, 43, 47]).

Let us end this introduction by describing the plan of the paper. In § 2 we fix notation and introduce some key quantities and bounds that will be used throughout the paper. In § 3 we gather some background on smooth metric measure spaces and prove some preliminary results on the evolution of geometric quantities of interest for time-dependent metrics and potentials. Section 4 which is the heart of the paper is devoted to the proof of the differential Harnack estimate in theorem 4.1 and its global version in theorem 4.5. Here as a consequence, we also prove a parabolic Harnack inequality for system (1.1). In § 5, we turn into the static case and present the counterparts of the Li–Yau estimates in the static context. We also prove a Liouville type constancy result and present some consequences of it. Finally, in § 6 we prove a Hamilton-type curvature free estimate and bounds using a different set of ideas. In this section, we assume the manifold is closed.

2. Local and global $\gamma$-quantities associated with the nonlinearity ${\mathscr G}$

To a given nonlinearity $\mathscr {G}=\mathscr {G}(t,\,x,\,w)$, we associate certain $\gamma$-quantities as defined below that will appear in different stages of the analysis and serve as bounds in various estimates. In order to describe these, for $\mathscr {G}$ of class ${\mathscr C}^2$ and constant $\mu$ we set,

(2.1)\begin{align} & \mathsf{A}_{\mathscr G}^\mu (t,x,w) = [- \mu w{\mathscr G}_{ww}(t,x,w) + {\mathscr G}_w(t,x,w) - {w^{{-}1} \mathscr G}(t,x,w)]_+, \end{align}

(2.2)\begin{align} & \mathsf{B}_{\mathscr G}^\mu (t,x,w) = |\mu {\mathscr G}_{xw}(t,x,w) - w^{{-}1} {\mathscr G}_x(t,x,w)|, \end{align}

(2.3)\begin{align} & \mathsf{C}_{\mathscr G} (t,x,w) = [{\mathscr G}_w(t,x,w) - w^{{-}1}{\mathscr G}(t,x,w)]_+, \end{align}

(2.4)\begin{align} & \mathsf{D}_{\mathscr G} (t,x,w) = [{-}w^{{-}1} \Delta_\phi {\mathscr G}^x(t,x,w)]_+. \end{align}

Here and below $z=z_+ + z_-$ with $z_+=\max (z,\, 0)$ and $z_-=\min (z,\, 0)$. The subscripts in ${\mathscr G}$ stand for the partial derivatives in the respective arguments and $\mathscr G^x: x \mapsto \mathscr G(t,\,x,\, w)$ denotes the function obtained by freezing the variables $t$, $w$ and viewing $\mathscr G$ as a function of $x$ only. (Thus in particular, we speak of $\nabla {\mathscr G}^x$ and $\Delta _\phi {\mathscr G}^x$.)

Fixing a reference point $x_0 \in M$, we denote by $d=d(x,\,x_0,\, t)$ the Riemannian distance between $x$ and $x_0$ with respect to the evolving metric $g=g(t)$. We write $r=r(x,\,x_0,\,t)$ for the geodesic radial variable measuring the distance between $x$ and $x_0$ at time $t>0$. For $R>0$, $T>0$, we define $Q_{R,T}(x_0) \equiv \{ (x,\, t): d(x,\, x_0,\, t) \le R,\, 0 \le t \le T \} \subset M \times [0,\, T]$ and for $0< t \le T$, we denote by $\mathscr {B}_r(x_0) \subset M$ the geodesic ball of radius $r>0$ centred at $x_0$. When the choice of the point $x_0$ is clear from the context, we often abbreviate and write $d(x,\, t)$, $r(x,\,t)$ or ${\mathscr B}_r$, $Q_{R,T}$ respectively.

Having the above notation in place, we now define the four pairs of local and global $\gamma$-quantities associated with a given $\mathscr G=\mathscr G(t,\,x,\,w)$ and $w=w(x,\,t)$ ($x \in M$, $0 \le t \le T$) by writing for fixed $x_0 \in M$, $R>0$ and $T>0$:

(2.5)\begin{align} & \gamma^{{\mathscr G}, \mu}_\mathsf{A} (R) = \sup_{\Theta_{R, T}} \mathsf{A}_{\mathscr G}^\mu (t,x,w),\quad \gamma^{{\mathscr G}, \mu}_\mathsf{A} = \sup_{M \times [0, T]} \mathsf{A}_{\mathscr G}^\mu (t,x,w), \end{align}

(2.6)\begin{align} & \gamma^{{\mathscr G}, \mu}_\mathsf{B} (R) = \sup_{\Theta_{R, T}} \mathsf{B}^\mu_{\mathscr G}(t,x,w),\quad \gamma^{{\mathscr G}, \mu}_\mathsf{B} = \sup_{M \times [0, T]} \mathsf{B}^\mu_{\mathscr G}(t,x,w), \end{align}

(2.7)\begin{align} & \gamma^{\mathscr G}_{\mathsf C} (R) = \sup_{\Theta_{R, T}} \mathsf{C}_{\mathscr G}(t,x,w),\quad \gamma^{\mathscr G}_{\mathsf C} = \sup_{M \times [0, T]} \mathsf{C}_{\mathscr G}(t,x,w), \end{align}

(2.8)\begin{align} & \gamma^{\mathscr G}_{\mathsf D} (R) = \sup_{\Theta_{R, T}} \mathsf{D}_{\mathscr G}(t,x,w), \quad \gamma^{\mathscr G}_{\mathsf D} = \sup_{M \times [0, T]} \mathsf{D}_{\mathscr G}(t,x,w). \end{align}

Here $\Theta _{R, T} = \{(t,\,x,\,w): (x,\,t) \in Q_{R,T},\, \, \underline w \le w \le \overline w \} \subset [0,\, T] \times M \times (0,\, \infty )$ where $\overline w$, $\underline w$ denote the maximum and minimum of $w$ on the compact space–time cylinder $Q_{R,T}$. Note that in the particular case ${\mathscr G}(t,\,x,\,w) = \mathsf a(x,\,t) w$ with ${\mathsf a}$ of class ${\mathscr C}^2$, we have:

(2.9)\begin{align} & \mathsf{A}_{\mathsf aw}^\mu (t,x,w) \equiv 0, \quad\mathsf{B}_{\mathsf aw}^\mu (t,x,w) = |(\mu -1) \nabla \mathsf a(x,t)|, \end{align}

(2.10)\begin{align} & \mathsf{C}_{\mathsf aw} (t,x,w) \equiv 0, \quad \mathsf{D}_{\mathsf aw} (x,t,w) = \left[ -\Delta_\phi \mathsf a(x,t) \right]_+, \end{align}

and subsequently

(2.11)\begin{align} & \gamma^{\mathsf aw, \mu}_\mathsf{B} (R) = |\mu -1| \sup_{Q_{R,T}} |\nabla \mathsf a(x,t)|\quad \gamma^{\mathsf aw, \mu}_\mathsf{B} = |\mu-1| \sup_{M \times [0, T]} |\nabla \mathsf a(x,t)|, \end{align}

(2.12)\begin{align} & \gamma^{\mathsf aw}_{\mathsf D} (R) = \sup_{Q_{R,T}} \left[ -\Delta_\phi \mathsf a(x,t) \right]_+,\quad \quad \,\, \gamma^{\mathsf aw}_{\mathsf D} = \sup_{M \times [0, T]} \left[ -\Delta_\phi \mathsf a(x,t) \right]_+, \end{align}

with all the remaining $\gamma$-quantities being zero.

3. Bakry–Èmery tensors and weighted Bochner–Weitzenbock formula

By a smooth metric measure space, we understand a triple $(M,\,g,\,d\sigma )$ in which $(M,\,g)$ is a complete Riemannian manifold, $d\sigma =e^{-\phi } dv_g$ is a weighted measure associated with the potential $\phi$, and $dv_g$ is the standard Riemannian volume measure. Both the metric tensor $g$ and the potential $\phi$ are assumed to be of class ${\mathscr C}^2$. The $\phi$-Laplacian (1.2) is a symmetric Markov diffusion operator with respect to the invariant measure $d\sigma$ and

(3.1)\begin{equation} {\mathscr Ric}^m_\phi(g) = {\mathscr Ric}(g) + \nabla\nabla \phi - \frac{\nabla \phi \otimes \nabla \phi}{m-n}, \end{equation}

is the Bakry–Èmery generalized Ricci curvature of the triple $(M,\,g,\,d\sigma )$. Here ${\mathscr Ric}(g)$ denotes the Riemannain Ricci curvature of $g$, $\nabla \nabla \phi ={\rm Hess}(\phi )$ is the Hessian of $\phi$, and $m \ge n$ is a constant (see [6–8]). For the sake of clarity, we point out that when $m=n$, by convention, $\phi$ is only allowed to be a constant, thus giving ${\mathscr Ric}^n_\phi (g)={\mathscr Ric}(g)$, whereas, by formally passing to the limit $m \to \infty$ in (3.1) we can also set,

(3.2)\begin{equation} {\mathscr Ric}^\infty_\phi(g) = {\mathscr Ric}(g) + \nabla\nabla \phi:= {\mathscr Ric}_\phi(g). \end{equation}

The following identity generalizing the classical Bochner–Weitzenböck formula in the Riemannian context to the smooth metric measure space context plays an important role throughout the paper (see [3, 28, 45, 46, 51]).

Lemma 3.1 Weighted Bochner–Weitzenböck formula

With $\Delta _\phi$ and ${\mathscr Ric}_\phi (g)$ as above, for any function $h \in {\mathscr C}^3(M)$ we have,

(3.3)\begin{equation} \frac{1}{2} \Delta_\phi |\nabla h|^2 = |\nabla\nabla h|^2 + \langle \nabla h, \nabla \Delta_\phi h \rangle + {\mathscr Ric}_\phi (\nabla h, \nabla h). \end{equation}

Next, making note of $(\Delta h)^2 \le n |\nabla \nabla h|^2$ and recalling $\Delta _\phi h = \Delta h - \langle \nabla \phi,\, \nabla h \rangle$ it is easily seen that

(3.4)\begin{equation} |\nabla\nabla h|^2 + \frac{\langle \nabla \phi , \nabla h \rangle^2}{m-n} \ge \frac{(\Delta h)^2}{n} + \frac{\langle \nabla \phi, \nabla h \rangle ^2}{m-n} \ge \frac{(\Delta h - \langle \nabla \phi, \nabla h \rangle)^2}{m} = \frac{(\Delta_\phi h)^2}{m}. \end{equation}

Therefore, from (3.1) and (3.3) it follows that

(3.5)\begin{equation} \frac{1}{2} \Delta_\phi |\nabla h|^2 \ge \frac{1}{m} (\Delta_\phi h)^2 + \langle \nabla h, \nabla \Delta_\phi h \rangle + {\mathscr Ric}^m_\phi (\nabla h, \nabla h). \end{equation}

Let us now present two useful identities on evolutionary metric-potential pairs that will be utilized later. For notational convenience we hereafter denote the metric time derivative tensor, i.e., the speed, as,

(3.6)\begin{equation} \frac{\partial g}{\partial t} (x,t) = 2 {\mathscr S} (x,t), \qquad (x,t) \in M \times (0, T), \end{equation}

(the factor $2$ is only for notational convenience). In the following lemmas, we assume that the evolutionary metric $g$ and potential $\phi$ are of class ${\mathscr C}^2$ in the space–time variables $(x,\,t)$.

Lemma 3.2 With notation (3.6) in place, for any pair of space–time functions $U=U(x,\,t)$ and $V=V(x,\,t)$ of class ${\mathscr C}^1$, we have

(3.7)\begin{equation} \partial_t \langle \nabla U, \nabla V \rangle ={-}2 {\mathscr S} (\nabla U, \nabla V) + \langle \nabla \partial_t U, \nabla V \rangle + \langle \nabla U, \nabla \partial_t V \rangle. \end{equation}

In particular $\partial _t |\nabla U|^2 = -2 {\mathscr S} (\nabla U,\, \nabla U) + 2 \langle \nabla U,\, \nabla \partial _t U \rangle$.

Proof. This follows by first writing $\langle \nabla U,\, \nabla V \rangle =g^{ij} \nabla _i U \nabla _j V$ and then taking $\partial _t$ making note of $\partial _t g^{ij} = - 2 g^{ik} g^{j \ell } {\mathscr S}_{k \ell } = -2{\mathscr S}^{ij}$. The second identity follows from the first one by setting $V=U$.

Lemma 3.3 With notation (3.6) in place, for any space–time function ${U=U(x,\,t)}$ of class ${\mathscr C}^2$, we have

(3.8)\begin{align} \partial_t( \Delta_\phi U ) & =\Delta_\phi (\partial_t U) - \langle 2{\mathscr S}, \nabla \nabla U \rangle - \langle 2 {\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S}),\nabla U \rangle \nonumber\\ & \quad- \langle \nabla \partial_t \phi , \nabla U \rangle + 2{\mathscr S} (\nabla \phi , \nabla U). \end{align}

Proof. Let us first consider the case where the potential $\phi$ is a constant (thus $\Delta _\phi =\Delta$). Indeed here we have the identity

(3.9)\begin{equation} \partial_t \Delta U = \Delta \partial_t U - \langle 2{\mathscr S}, \nabla \nabla U \rangle - \langle 2{\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S}), \nabla U \rangle. \end{equation}

Now to justify (3.8) we proceed by directly calculating $\partial _t \Delta _\phi U = \partial _t(\Delta U - \langle \nabla \phi,\, \nabla U \rangle )$ whilst making note of (3.7) and (3.9). Hence we can write

(3.10)\begin{align} \partial_t \Delta_\phi U & =\Delta (\partial_t U) - \langle 2{\mathscr S}, \nabla \nabla U \rangle - \langle 2 {\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S}),\nabla U \rangle \nonumber\\ & \quad- \langle \nabla \partial_t \phi , \nabla U \rangle - \langle \nabla \phi, \nabla \partial_t U \rangle + 2{\mathscr S} \langle \nabla \phi , \nabla U \rangle \nonumber\\ & =\Delta_\phi (\partial_t U) - \langle 2{\mathscr S}, \nabla \nabla U \rangle - \langle 2 {\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S}),\nabla U \rangle \nonumber\\ & \quad- \langle \nabla \partial_t \phi , \nabla U \rangle + 2{\mathscr S} (\nabla \phi , \nabla U), \end{align}

which is the required conclusion. The proof is thus complete.

4. A differential Harnack estimate for system (1.1) under $(\mathsf {k},\,m)$-super Perelman–Ricci flow

In this section, we formulate and prove a differential Harnack estimate for positive smooth solutions to the nonlinear parabolic equation $(\partial _t - \mathsf a(x,\,t)- \Delta _\phi ) w = \mathscr G (t,\,x,\,w)$ where the metric and potential evolves under a $(\mathsf {k},\,m)$-super Perelman–Ricci flow. This means that the pair $(g,\, \phi )$ forms a complete smooth solution to the flow inequality (4.1) [with $n \le m < \infty$, $(x,\, t) \in M \times [0,\, T]$ and the choice of constant $\mathsf {k}=\mathsf {k}_m=(m-1)k+k^L$ (see (4.2) and (4.3) below)]

(4.1)\begin{equation} \begin{cases} \dfrac{1}{2} \dfrac{\partial g}{\partial t} (x,t) + {\mathscr Ric}_\phi^m(g)(x,t) \ge - \mathsf{k}g(x,t), \\ {\mathscr Ric}_\phi^m(g)(x,t) = {\mathscr Ric} (g)(x,t) + \nabla_{g(t)} \nabla_{g(t)} \phi (x,t) - \dfrac{\nabla_{g(t)} \phi \otimes \nabla_{g(t)} \phi}{m-n} (x,t). \end{cases} \end{equation}

For future reference we also make note of the following bounds relating to the metric-potential pair $(g,\,\phi )$ [recall (3.6)]. For suitable constants $k^L,\, k^U,\, k^\nabla \ge 0$, $\ell _1,\, \ell _2 \ge 0$:

(4.2)\begin{align} -k^L g & \le {\mathscr S} \le k^U g, \qquad |\nabla {\mathscr S}| \le k^\nabla, \end{align}

(4.3)\begin{align} |\nabla \phi| & \le \ell_1, \qquad |\nabla \partial_t \phi| \le \ell_2. \end{align}

Theorem 4.1 Let $(M,\, g,\, d\sigma )$ be a smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and time dependent metric-potential pair $(g,\, \phi )$ of class $\mathscr {C}^2$. Assume ${\mathscr Ric}_\phi ^m(g) \ge -(m-1) k g$ in $Q_{2R,T}$ for some $m \ge n$, $k \ge 0$ and $R,\,T>0$ and bounds (4.2)–(4.3) hold in $Q_{2R,T}$. If $w=w(x,\,t)$ is a positive solution to (1.1), then for every $\mu >1$, $\varepsilon \in (0,\, 1)$ and for all $(x,\,t)$ in $Q_{R,T}$ with $t>0$ we have the gradient estimate

(4.4)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} - \frac{\partial_t w}{w} + \frac{\mathscr G(t,x,w)}{w} +\mathsf a(x,t) \le \frac{m \mu}{t} + m \mu c_1 k^L + \mathsf{L} + m \mu \gamma^{\mathscr G}_{\mathsf C} (2R) + \mathsf{M}_\mathsf a^\mathscr G. \end{equation}

The quantities appearing on the right-hand side of bound (4.4) are given respectively by

(4.5)\begin{equation} \mathsf{L} =\frac{m \mu}{R^2} \left[ \frac{m c_1 ^2 \mu ^2}{2(\mu -1)}+c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2 \right] \end{equation}

and

(4.6)\begin{align} \mathsf{M}_\mathsf a^\mathscr G & = \sqrt m \left\{\vphantom{\left[ \frac{m \mu^2 [\mu \ell_2 + 2 \mu k^L \ell_1+ 2\gamma^{{\mathscr G}, \mu}_\mathsf{B} (2R) + 2\gamma^{\mathsf aw, \mu}_\mathsf{B} (2R)]^4}{4 \varepsilon(\mu-1)^2} \right]^{1/3}}n\mu ^2 (k^L + k^U)^2 + 2n \mu^2 k^\nabla + \mu \gamma^{\mathscr G}_{\mathsf D} (2R) + \mu \gamma^{\mathsf aw}_{\mathsf D}(2R)\right. \nonumber\\ & \quad+ \left.\frac{4\,m \mu^2 [(m-1) k +(\mu -1) k^U + k^\nabla + \gamma^{{\mathscr G}, \mu}_\mathsf{A} (2R)/2]^2}{4(1-\varepsilon)(\mu-1)^2}\right.\nonumber\\ & \quad+\left. \frac{3}{4} \left[ \frac{m \mu^2 [\mu \ell_2 + 2 \mu k^L \ell_1+ 2\gamma^{{\mathscr G}, \mu}_\mathsf{B} (2R) + 2\gamma^{\mathsf aw, \mu}_\mathsf{B} (2R)]^4}{4 \varepsilon(\mu-1)^2} \right]^{1/3}\right\}^{1/2}. \end{align}

The $\gamma$-quantities in (4.4) and (4.6) are as in (2.5)–(2.8) and (2.11)–(2.12) $($with $2R$ replacing $R)$ and the constants $c_1$, $c_2>0$ in (4.5) are as in (4.19) in lemma 4.4.

As the proof of the theorem is quite involved and requires several intermediate steps, for the sake of reader's convenience we present this in several stages. The first task is to introduce a Harnack quantity built out of the solution $w$ and consider its evolution under the weighted heat operator.

Lemma 4.2 Let $w$ be a positive solution to the equation ${\mathscr L}_\phi ^{\mathsf a} [w] = (\partial _t -\mathsf a(x,\,t)- \Delta _\phi ) w = \mathscr G (t,\,x,\,w)$ and let $F_\mathsf a^\mathscr G=F_\mathsf a^\mathscr G(x,\,t)$ be defined by

(4.7)\begin{equation} F^\mathscr G_\mathsf a (x,t) = t [|\nabla f|^2 - \mu \partial_t f + \mu \mathsf a(x,t) + \mu e^{{-}f} \mathscr G(t,x,e^f)], \quad t \ge 0, \end{equation}

where $f =\log w$ and $\mu >1$ is a fixed constant. Suppose that the metric-potential pair $(g,\, \phi )$ is time dependent and of class $\mathscr {C}^2$. Then $F^\mathscr G_\mathsf a$ satisfies

(4.8)\begin{align} (\Delta_\phi - \partial_t) [F^\mathscr G_\mathsf a] & = ~2 t|\nabla \nabla f |^2 - 2 \langle \nabla f , \nabla F^\mathscr G_\mathsf a \rangle +2t {\mathscr Ric}_\phi^m (\nabla f, \nabla f) \nonumber\\ & \quad- 2t (\mu -1) {\mathscr S}(\nabla f, \nabla f) + 2t \langle \nabla \phi , \nabla f \rangle^2/(m-n) - F^\mathscr G_\mathsf a/t \nonumber\\ & \quad- 2 \mu t [\langle {\mathscr S}, \nabla \nabla 2 f \rangle + \langle {\rm div} {\mathscr S} - (1/2) \nabla ({\rm Tr}_g {\mathscr S}),\nabla f \rangle] \nonumber\\ & \quad- \mu t[\langle \nabla \partial_t \phi , \nabla f \rangle- 2{\mathscr S} (\nabla \phi , \nabla f) ] \nonumber\\ & \quad+ 2t (\mu -1) \langle \nabla f , \nabla \mathsf a(x,t) \rangle + \mu t \Delta_\phi[\mathsf a(x,t)] \nonumber\\ & \quad+2t (\mu -1) \langle \nabla f, \nabla [e^{{-}f}\mathscr G(t,x,e^f)] \rangle + \mu t \Delta_\phi [e^{{-}f} \mathscr G (t,x,e^f)]. \end{align}

Proof. Referring to the equation for $w$ an easy calculation shows that $f$ satisfies the equation

(4.9)\begin{equation} {\mathscr L}_\phi [f] = (\partial_t - \Delta_\phi) f = |\nabla f|^2 + e^{{-}f} \mathscr G(t,x,e^f) +\mathsf a(x,t). \end{equation}

Moreover, using (4.7) and (4.9) it is a straightforward matter to see that the following relation holds between $F^\mathscr G_\mathsf a$ and $\Delta _\phi f$:

(4.10)\begin{align} \Delta_\phi f & ={-} \left[ \mu^{{-}1} |\nabla f|^2 - \partial_t f +\mathsf a(x,t) + e^{{-}f} \mathscr G(t,x,e^f) \right] - (1-\mu^{{-}1}) |\nabla f|^2 \nonumber\\ & ={-} F^\mathscr G_\mathsf a/(\mu t) - (1-\mu^{{-}1}) |\nabla f|^2, \qquad t>0. \end{align}

We next calculate the different ingredients needed in the application of the weighted heat operator ${\mathscr L}_\phi =\partial _t - \Delta _\phi$ to the Harnack quantity in (4.7). To this end we first note that

(4.11)\begin{equation} \Delta_\phi F^\mathscr G_\mathsf a = t (\Delta_\phi |\nabla f|^2 - \mu \Delta_\phi (\partial_t f) + \mu \Delta_\phi \mathsf a(x,t) + \mu \Delta_\phi [e^{{-}f}\mathscr G(t,x,e^f)]). \end{equation}

Recalling the weighted Bocnher–Weitzenböck formula in lemma 3.1 as applied to $f$ and making use of (3.8) in lemma 3.3 we then have

(4.12)\begin{align} \Delta_\phi F^\mathscr G_\mathsf a & =t \left[ 2 |\nabla \nabla f |^2 +2 \langle \nabla f, \nabla \Delta_\phi f \rangle +2 {\mathscr Ric}_\phi^m (\nabla f, \nabla f)+2\langle \nabla \phi , \nabla f \rangle^2/(m-n) \right] \nonumber\\ & \quad-\mu t \partial_t (\Delta_\phi f) -2\mu t \left[ \langle {\mathscr S}, \nabla \nabla f \rangle + \langle {\rm div} {\mathscr S} - (1/2)\nabla ({\rm Tr}_g {\mathscr S}),\nabla f \rangle \right] \\ & \quad-\mu t [\langle \nabla \partial_t \phi , \nabla f \rangle - 2{\mathscr S} ( \nabla \phi , \nabla f )] + \mu t \Delta_\phi[\mathsf a(x,t)]+ \mu t \Delta_\phi [e^{{-}f} \mathscr G (t,x,e^f)]. \nonumber \end{align}

Now referring to the sum on the right, the contributions of the second and fifth terms modulo a factor $t$ can be simplified and rewritten upon using (4.9) and (4.10) as,

(4.13)\begin{align} & 2 \langle \nabla f,\nabla \Delta_\phi f \rangle - \mu \partial_t(\Delta_\phi f) \nonumber\\ & \quad=2 \langle \nabla f, \nabla \Delta_\phi f \rangle +2 (\mu -1) \langle \nabla f , \nabla [\Delta_\phi f +|\nabla f|^2 + e^{{-}f}\mathscr G (t,x,e^f)+\mathsf a(x,t)]\rangle \nonumber\\ & \qquad+ (t \partial_t F^\mathscr G_\mathsf a - F^\mathscr G_\mathsf a)/t^2 - 2 (\mu -1) {\mathscr S} (\nabla f , \nabla f) \nonumber\\ & \quad =2 \langle \nabla f , \nabla [{-}F^\mathscr G_\mathsf a/t - (\mu -1) |\nabla f|^2] \rangle +2(\mu -1) \langle \nabla f, \nabla |\nabla f|^2 \rangle + (t \partial_t F^\mathscr G_\mathsf a - F^\mathscr G_\mathsf a)/t^2\nonumber\\ & \qquad+ 2(\mu-1) \langle \nabla f , \nabla \mathsf a(x,t) \rangle + 2 (\mu -1) \langle \nabla f , \nabla [e^{{-}f}\mathscr G (t,x,e^f)]\rangle \nonumber\\ & \qquad - 2 (\mu -1) {\mathscr S} (\nabla f , \nabla f)\nonumber\\ & \quad=2 (\mu -1) [\langle \nabla f , \nabla \mathsf a(x,t) \rangle + \langle \nabla f , \nabla [e^{{-}f}\mathscr G (t,x,e^f)] \rangle - {\mathscr S} (\nabla f , \nabla f)]\nonumber\\ & \qquad+ (t\partial_t F^\mathscr G_\mathsf a - F^\mathscr G_\mathsf a)/t^2 - 2 \langle \nabla f , \nabla F^\mathscr G_\mathsf a \rangle/t. \end{align}

Therefore, substituting this expression back into (4.12) and rearranging terms lead to

(4.14)\begin{align} (\Delta_\phi - \partial_t) [F^\mathscr G_\mathsf a] & = 2 t|\nabla \nabla f |^2 +2t (\mu -1)[ \langle \nabla f , \nabla \mathsf a \rangle \nonumber\\ & \quad+ \langle \nabla f, \nabla[e^{{-}f}\mathscr G(t,x,e^f)] \rangle - {\mathscr S} (\nabla f, \nabla f)] \nonumber\\ & \quad- F^\mathscr G_\mathsf a /t -2 \langle \nabla f , \nabla F^\mathscr G_\mathsf a \rangle \nonumber\\ & \quad + 2t {\mathscr Ric}_\phi^m (\nabla f, \nabla f) +2t \langle \nabla \phi , \nabla f \rangle^2/(m-n) \nonumber\\ & \quad- 2\mu t \langle {\mathscr S}, \nabla \nabla f \rangle - \mu t \langle 2 {\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S}),\nabla f \rangle - \mu t \langle \nabla \partial_t \phi , \nabla f \rangle\nonumber\\ & \quad+2 \mu t {\mathscr S} (\nabla \phi , \nabla f) + \mu t \Delta_\phi \mathsf a+ \mu t \Delta_\phi[ e^{{-}f} \mathscr G (t,x,e^f)] \end{align}

which is the desired conclusion.

Lemma 4.3 Let $w$ be a positive solution to ${\mathscr L}_\phi ^{\mathsf a}[f]=(\partial _t -\mathsf a(x,\,t)- \Delta _\phi ) w =\mathscr G (t,\,x,\,w)$ and let $F$ be as in (4.7). Assume the metric-potential pair $(g,\, \phi )$ is time dependent and of class $\mathscr {C}^2$. Moreover assume the bounds ${\mathscr Ric}_\phi ^m (g) \ge -(m-1) kg$ and

(4.15)\begin{equation} - k^L g \le {\mathscr S} \le k^U g, \qquad |\nabla {\mathscr S}| \le k^\nabla, \end{equation}

for suitable $k,\, \underline k^L,\, k^U$ and $k^\nabla \ge 0$. Then

(4.16)\begin{align} (\Delta_\phi - \partial_t) [F^\mathscr G_\mathsf a] & \ge t (\Delta_\phi f)^2/m - F^\mathscr G_\mathsf a/t -2 \langle \nabla f, \nabla F^\mathscr G_\mathsf a \rangle \nonumber\\ & \quad- 2t [(m-1)k +(\mu -1) k^U] |\nabla f|^2\nonumber\\ & \quad-\mu^2 n t(k^L+k^U)^2 -3 \mu t\sqrt n k^\nabla |\nabla f| \nonumber\\ & \quad- \mu t \langle \nabla \partial_t \phi , \nabla f \rangle + 2\mu t {\mathscr S} ( \nabla \phi , \nabla f ) \nonumber\\ & \quad+ 2 (\mu -1) t \langle \nabla f,\nabla \mathsf a(x,t) \rangle +\mu t\Delta_\phi [\mathsf a(x,t)]\nonumber\\ & \quad+ 2 (\mu -1) t \langle \nabla f,\nabla [e^{{-}f} \mathscr G(t,x,e^f)] \rangle +\mu t\Delta_\phi [e^{{-}f} \mathscr G(t,x,e^f)]. \end{align}

Proof. From the upper and lower bounds on ${\mathscr S}$ in the sense of symmetric $2$-tensors in (3.6)–(4.15) it follows that $|{\mathscr S}|^2 \le (k^L+k^U)^2 |g|^2 = n(k^L+k^U)^2$ and hence

(4.17)\begin{align} 2 |\mu \langle {\mathscr S}, \nabla \nabla f \rangle| \le |\nabla \nabla f|^2 + \mu ^2 |{\mathscr S}|^2 \le |\nabla \nabla f|^2 + n\mu^2(k^L+k^U)^2. \end{align}

Moreover by virtue of the assumption $|\nabla {\mathscr S}| \le k^\nabla$ we have

(4.18)\begin{align} |2{\rm div} {\mathscr S} - \nabla ({\rm Tr}_g {\mathscr S})| & = \left| 2g^{ij} \nabla_i {\mathscr S}_{j \ell} - g^{ij} \nabla_\ell {\mathscr S}_{ij} \right| = \left| g^{ij} (2 \nabla_i {\mathscr S}_{j \ell} - \nabla_\ell {\mathscr S}_{ij}) \right| \nonumber\\ & \le 3 |g| |\nabla {\mathscr S}| \le 3\sqrt n k^\nabla. \end{align}

Now the conclusion follows at once by referring (4.8) in lemma 4.2, making note of the bound $|\nabla \nabla f|^2+\langle \nabla \phi,\, \nabla f \rangle ^2/(m-n) \ge (\Delta f)^2/n+\langle \nabla \phi,\, \nabla f \rangle ^2/(m-n) \ge (\Delta _\phi f)^2/m$, and the Bakry–Èmery curvature lower bound ${\mathscr Ric}_\phi ^m \geq -(m-1) k g$ in the lemma.

For the purpose of localization we shall make use of standard spatial cut-off functions. To this end we note the following lemma gathering together some of the main properties of a profile function defined on the half-line $s \ge 0$ as needed later (see [4, 11, 28, 29, 54]).

Lemma 4.4 There exists a function $\bar {\psi }:[0,\,\infty ) \to \mathbb {R}$ satisfying the following properties:

1. (i) $\bar \psi$ is of class $\mathscr {C}^2 [0,\, \infty )$.

2. (ii) $0 \le \bar \psi (s) \le 1$ for $0 \le s < \infty$ and $\bar {\psi } \equiv 1$ on $[0,\,1]$ and $\bar {\psi } \equiv 0$ on $[2,\, \infty )$.

3. (iii) $\bar \psi ' \le 0$ and so $\bar \psi$ is non-increasing and for suitable constants $c_1,\, c_2>0$ we have the global bounds

   (4.19)\begin{equation} - c_1 \bar\psi^{1/2} \le \bar\psi' \le 0, \text{ and } \bar{\psi}^{''} \ge -c_2. \end{equation}

Now, we pick a reference point $x_0 \in M$, fix $R,\, T>0$ and $0<\tau \le T$ and then with $r(x,\,t)$ denoting the geodesic radial variable with respect to $x_0$ at time $t$, set

(4.20)\begin{equation} \psi(x,t)=\bar{\psi} (r (x, t)/R), \qquad x \in M, 0 \le t \le T. \end{equation}

It is evident that the resulting function $\psi$ satisfies $\psi \equiv 1$ for when $0 \le r(x,\, t) \le R$ and $\psi \equiv 0$ for when $r(x,\,t) \ge 2R$. Additionally from (4.20) we have $\nabla \psi = (\bar \psi '/R) \nabla r$ and $\Delta \psi = \bar \psi ' |\nabla r|^2/R^2+\bar \psi ' \Delta r/R$ and so $\Delta _\phi \psi = \Delta \psi - \langle \nabla \phi,\, \nabla \psi \rangle = \bar \psi '' |\nabla r|^2/R^2+\bar \psi ' \Delta _\phi r/R$. In particular $\nabla \psi$, $\Delta _\phi \psi$ vanish outside the space–time set $R \le r(x,\,t) \le 2R$.

Proof of theorem 4.1 Consider the localized function $\psi F^\mathscr G_\mathsf a$ where $F^\mathscr G_\mathsf a$ is the Harnack quantity in (4.7). Let $(x_1,\,t_1)$ denote the point where this function attains its maximum over the compact cylinder $\{r(x,\,t) \le 2R,\, 0 \le t \le \tau \}$. We assume $[\psi F^\mathscr G_\mathsf a] (x_1,\, t_1)>0$ as otherwise the estimate follows from $F^\mathscr G_\mathsf a \le 0$. So in particular $t_1>0$ and $r(x_1,\, t_1) < 2R$ and therefore, at the maximum point $(x_1,\, t_1)$, we have the relations

(4.21)\begin{equation} \begin{cases} \partial_t (\psi F^\mathscr G_\mathsf a) \ge 0, \\ \nabla (\psi F^\mathscr G_\mathsf a)=0, \\ \Delta(\psi F^\mathscr G_\mathsf a) \le 0, \\ \Delta_\phi (\psi F^\mathscr G_\mathsf a) \le 0. \end{cases} \end{equation}

Utilizing the product identity for the $\phi$-Laplacian as applied to the localized function $\psi F^\mathscr G_\mathsf a$ we can write

(4.22)\begin{equation} \Delta_\phi (\psi F^\mathscr G_\mathsf a) = F^\mathscr G_\mathsf a \Delta_\phi \psi + 2 \langle \nabla \psi, \nabla F^\mathscr G_\mathsf a \rangle + \psi \Delta_\phi F^\mathscr G_\mathsf a, \end{equation}

and so making note of relations (4.21) at the maximum point $(x_1,\, t_1)$ we can further deduce

(4.23)\begin{align} 0 & \ge F^\mathscr G_\mathsf a \Delta_\phi \psi + 2 \langle \nabla \psi, \nabla F^\mathscr G_\mathsf a \rangle + \psi \Delta_\phi F^\mathscr G_\mathsf a \nonumber\\ & \ge F^\mathscr G_\mathsf a \Delta_\phi \psi + (2/\psi) \langle \nabla \psi , \nabla (\psi F^\mathscr G_\mathsf a) \rangle -2 (|\nabla \psi |^2/\psi) F^\mathscr G_\mathsf a + \psi \Delta_\phi F^\mathscr G_\mathsf a \nonumber\\ & \ge F^\mathscr G_\mathsf a \Delta_\phi \psi -2 (|\nabla \psi |^2/\psi) F^\mathscr G_\mathsf a + \psi \Delta_\phi F^\mathscr G_\mathsf a. \end{align}

Let us now proceed by bounding the sum on the right-hand side of (4.23) from below. To this end starting with the first term we have

(4.24)\begin{equation} \Delta_\phi \psi \ge -\frac{1}{R^2}[c_2 +(m-1) c_1(1+R \sqrt{k})], \end{equation}

where $c_1,\, c_2>0$ are as in lemma 4.4. In fact, since ${\mathscr Ric}_\phi ^m (g) \ge -(m-1) k g$ it follows from the Wei–Wylie weighted Laplacian comparison theorem, the $\phi$-Laplacian relation $\Delta _\phi \psi = \bar \psi ' |\nabla r|^2/R^2+\bar \psi ' \Delta _\phi r/R$ and the bounds in lemma 4.4 that,

(4.25)\begin{align} \Delta_\phi \psi & \ge \frac{1}{R^2} \bar\psi' + \frac{(m-1)}{R} \bar\psi' \sqrt{k} \coth (\sqrt{k} r)\ge \frac{1}{R^2} \bar\psi' + \frac{(m-1)}{R} \bar\psi' \sqrt{k} \coth (\sqrt{k} R) \nonumber\\ & \ge \frac{1}{R^2} \bar\psi' + (m-1) \frac{1+\sqrt{k}R}{R} \bar\psi' \ge -\frac{c_2}{R^2}-(m-1)\frac{c_1}{R} \left(\frac{1}{R}+\sqrt{k}\right), \end{align}

by virtue of $\Delta _\phi r \le (m-1) \sqrt {k}\coth (\sqrt {k} r)$ and $\Delta _\phi \psi \equiv 0$ outside $R \le r \le 2R$. Note that here we have used the monotonicity of $s \mapsto \coth s$ and $s \coth s \le (1 + s)$ for $s>0$. Onto the second term on the right in (4.23), again by (4.20) and lemma 4.4 we have,

(4.26)\begin{equation} \frac{|\nabla \psi |^2}{\psi} = \frac{\bar\psi'^2}{\bar\psi} \frac{|\nabla r|^2}{R^2} = \left( \frac{\bar\psi'}{\sqrt {\bar\psi}} \frac{|\nabla r|}{R} \right)^2 \le \frac{c_1 ^2}{R^2}. \end{equation}

Now making use of (4.16), (4.24) and (4.26) and substituting in (4.23) it follows that at the maximum point $(x_1,\, t_1)$ we have the inequality

(4.27)\begin{align} 0 & \ge F^\mathscr G_\mathsf a \Delta_\phi \psi -2 (|\nabla \psi |^2/\psi) F^\mathscr G_\mathsf a + \psi \Delta_\phi F^\mathscr G_\mathsf a \nonumber\\ & \ge -[c_2 +(m-1) c_1(1+R \sqrt{k})] F^\mathscr G_\mathsf a/R^2 - 2 (c_1^2/R^2) F^\mathscr G_\mathsf a + \psi \partial_t F^\mathscr G_\mathsf a \nonumber\\ & \quad+ \psi [ (t_1/m) (\Delta_\phi f)^2 - F^\mathscr G_\mathsf a/t_1 -2 \langle \nabla f, \nabla F^\mathscr G_\mathsf a \rangle -2 [(m-1)k +(\mu -1) k^U] t_1 |\nabla f|^2\nonumber\\ & \quad-\mu^2 n t_1(k^L+k^U)^2 -3 \sqrt n k^\nabla \mu t_1 |\nabla f| -\mu t_1 \langle \nabla \partial_t \phi , \nabla f \rangle + 2\mu t_1 {\mathscr S} ( \nabla \phi , \nabla f)\nonumber\\ & \quad+ 2 (\mu -1) t_1 [\langle \nabla f, \nabla \mathsf a \rangle+\langle \nabla f,\nabla (e^{{-}f} \mathscr G)\rangle] +\mu t_1 [\Delta_\phi \mathsf a +\Delta_\phi (e^{{-}f} \mathscr G)] ]. \end{align}

For the sake of convenience in writing here and below we abbreviate the arguments of $\mathsf a=\mathsf a(x,\,t)$ and $\mathscr G=\mathscr G(t,\,x,\,e^f)$. The aim is now to bound each of the individual terms in the last inequality. Starting from the third term on the second line $\psi \partial _t F^\mathscr G_\mathsf a$, upon recalling (4.20), we have,

(4.28)\begin{equation} \partial_t(\psi F^\mathscr G_\mathsf a) = \psi \partial_t F^\mathscr G_\mathsf a + F^\mathscr G_\mathsf a \partial_t \psi = \bar \psi(r/R) \partial_t F^\mathscr G_\mathsf a + \bar\psi' (r/R) F^\mathscr G_\mathsf a \partial_t r/R.\end{equation}

Now as at the maximum point $(x_1,\, t_1)$ we have $\partial _t (\psi F^\mathscr G_\mathsf a) \ge 0$, by restricting to this point, utilizing lemma 4.4 [the left inequality in (4.19)] and the bound $\partial _t r(x,\,t) \ge -k^L r(x,\,t)$ [see (4.30)], we can write

(4.29)\begin{align} \psi \partial_t F^\mathscr G_\mathsf a & \ge - F^\mathscr G_\mathsf a \partial_t \psi ={-} \bar \psi' (r/R) F^\mathscr G_\mathsf a \partial_t r/R \nonumber\\ & \ge rk^L F^\mathscr G_\mathsf a \bar\psi' (r/R)/R \ge -c_1 r k^L \sqrt{\bar\psi (r/R)} F^\mathscr G_\mathsf a/R \ge - c_1 k^L F^\mathscr G_\mathsf a. \end{align}

The justification for the lower bound on $\partial _t r(x_1,\,t_1)$ used above can be given as follows. Fix $x$ and $t$ such that $d(x,\, x_0,\, t)<2R$. Let $X(x_0,\,x)$ be the set of all minimal geodesics $\zeta =\zeta (s): [0,\, 1] \to M$ with respect to $g(t)$ connecting the reference point $x_0 =\zeta (0)$ to $x=\zeta (1)$ and let $\Gamma (x_0,\,x)$ be the set of all ${\mathscr C}^1$ curves connecting $x_0$ to $x$. Using the lower bound $\partial _t g = 2 {\mathscr S} \ge -2 k^L g$ in $Q_{2R,T}$ as given by (4.2) with $k^L \ge 0$ and Lemma B.40 p. 531 in [16] we can write:

(4.30)\begin{align} \partial_t r (x,t) & = \frac{\partial}{\partial t} d (x, x_0; t) \nonumber\\ & = \frac{\partial}{\partial t} \left\{ \inf_{\gamma \in \Gamma(x_0, x)} \int_0^1 |\gamma'(s)|_{g(t)} \, {\rm d}s \right\} \nonumber\\ & = \frac{\partial}{\partial t} \left\{ \inf_{\gamma \in \Gamma(x_0, x)} \int_0^1 \sqrt{[g(t)] (\gamma'(s), \gamma'(s))} \, {\rm d}s \right\} \nonumber\\ & = \inf_{\zeta \in X(x_0,x)} \int_0^1 \frac{[\partial_t g](\zeta'(s), \zeta'(s))}{2 \sqrt{[g(t)] (\zeta'(s), \zeta'(s))}} \, {\rm d}s = \inf_{\zeta \in X(x_0,x)} \int_0^1 \frac{{\mathscr S}(\zeta'(s), \zeta'(s))}{|\zeta'(s)|_{g(t)}} \, {\rm d}s \nonumber\\ & \ge \inf_{\zeta \in X(x_0,x)} \int_0^1 - k^L |\zeta' (s)|_{g(t)} \, {\rm d}s = \inf_{\zeta \in X(x_0,x)} \left[ - k^L \overbrace{\int_0^1 |\zeta' (s)|_{g(t)} \, {\rm d}s}^{{=}r(x,t)} \right] \nonumber\\ & \ge - k^L r(x, t) \ge - k^L R, \end{align}

which is the desired bound. (We note that this can also be derived using the evolution formula of the geodesic length under geometric flow due to R. Hamilton [24].) Next, in view of $\nabla (\psi F^\mathscr G_\mathsf a) =0$ at $(x_1,\, t_1)$ we can write,

(4.31)\begin{equation} \psi \langle \nabla f, \nabla F^\mathscr G_\mathsf a \rangle ={-}F^\mathscr G_\mathsf a \langle \nabla f , \nabla \psi \rangle \le F^\mathscr G_\mathsf a |\nabla f| |\nabla \psi| \le c_1 (\sqrt \psi/R) F^\mathscr G_\mathsf a |\nabla f|.\end{equation}

Likewise, we have ${\mathscr S} (\nabla \phi,\, \nabla f) \le k^L |\nabla \phi | |\nabla f|$ and $\langle \nabla \partial _t \phi,\, \nabla f \rangle \le |\nabla \partial _t \phi | |\nabla f|$ along with $3 k^\nabla \sqrt n \mu |\nabla f| \le 2 n k^\nabla \mu ^2 + 2 k^\nabla |\nabla f|^2$. Hence substituting all the above back in (4.27) it follows that

(4.32)\begin{align} 0 & \ge - [c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2] F^\mathscr G_\mathsf a/R^2 \nonumber\\ & \quad- c_1 k^L F^\mathscr G_\mathsf a - 2c_1 (\sqrt \psi/R) F^\mathscr G_\mathsf a |\nabla f| + t_1 (\psi/m) (\Delta_\phi f)^2 \nonumber\\ & \quad- \psi F^\mathscr G_\mathsf a/t_1 - 2t_1 [(m-1)k +(\mu -1) k^U] \psi |\nabla f|^2 \nonumber\\ & \quad- t_1 \psi [\mu^2 n (k_L+k^U)^2 + 2 n k^\nabla \mu^2 + 2 k^\nabla |\nabla f|^2] \nonumber\\ & \quad - \mu t_1 \psi [2k^L |\nabla \phi| |\nabla f| + |\nabla \partial_t \phi| |\nabla f|] \nonumber\\ & \quad+ 2t_1 \psi (\mu -1) [\langle \nabla f , \nabla \mathsf a \rangle+\langle \nabla f,\nabla (e^{{-}f} \mathscr G) \rangle]\nonumber\\ & \quad+ t_1 \psi \mu [\Delta_\phi \mathsf a+\Delta_\phi (e^{{-}f} \mathscr G)]. \end{align}

Next multiplying (4.32) through by the factor $t_1 \psi (x_1)=t_1 \psi$, making note of (4.9) and rearranging terms gives

(4.33)\begin{align} 0 & \geq{-}t_1 \psi F^\mathscr G_\mathsf a ([c_2 +(m-1) c_1(1+R \sqrt{k})] + 2c_1^2)/R^2 - \psi^2 F^\mathscr G_\mathsf a \nonumber\\ & \quad- c_1 k^L t_1 \psi F^\mathscr G_\mathsf a + t_1^2 (\psi ^2/m) \left[|\nabla f|^2 + e^{{-}f}\mathscr G + \mathsf a- \partial_t f\right]^2 \nonumber\\ & \quad- 2c_1 t_1 \psi (\sqrt \psi/R) F^\mathscr G_\mathsf a|\nabla f| -2 t_1^2 \left[(m-1)k +(\mu -1) k^U+k^\nabla \right] \psi^2 |\nabla f|^2 \nonumber\\ & \quad- n \mu^2 t_1^2 \psi ^2[ (k^L+k^U)^2+ 2 k^\nabla] -\mu t_1^2 \psi^2 |\nabla \partial_t \phi| |\nabla f| - 2\mu t_1^2 \psi ^2 k^L |\nabla \phi| |\nabla f|\nonumber\\ & \quad+ t_1^2 \psi ^2 \{2(\mu -1)[\langle \nabla f , \nabla \mathsf a \rangle +\langle \nabla f,\nabla (e^{{-}f} \mathscr G) \rangle] + \mu [\Delta_\phi \mathsf a+\Delta_\phi (e^{{-}f} \mathscr G)]\}. \end{align}

Let us now pause briefly to go through some calculations relating to $\mathscr G=\mathscr G(t,\,x,\, w)$ with $w=e^f$ and $f=f(x,\,t)$ needed below. Note that the arguments of the functions involved will be abbreviated for the sake of convenience in writing. Firstly,

(4.34)\begin{equation} \nabla \mathscr G = \mathscr G_x + e^f \mathscr G_w\nabla f, \quad \mathscr G_x=(\mathscr G_{x_1}, \dots, \mathscr G_{x_n}). \end{equation}

Upon introducing the notation $\mathscr G^x: x \mapsto \mathscr G(t,\,x,\, w)$ (i.e., viewing $\mathscr G$ as a function of $x$ whilst freezing the variable $w$) we can write

(4.35)\begin{align} \Delta \mathscr G & =\Delta \mathscr G^x+e^f \langle \mathscr G_{xw} + e^f |\nabla f|^2 \mathscr G_w ,\nabla f \rangle \nonumber\\ & \quad+e^f \langle \mathscr G_{xw},\nabla f \rangle +e^{2f} |\nabla f|^2 \mathscr G_{ww} +e^f \mathscr G_w \Delta f \nonumber\\ & = \Delta \mathscr G^x+2e^f \langle \mathscr G_{xw} ,\nabla f \rangle + e^f |\nabla f|^2 ( \mathscr G_w +e^f \mathscr G_{ww})+e^f \mathscr G_w \Delta f. \end{align}

Subsequently calculating the $\phi$-Laplacian, by utilizing the above fragments we have,

(4.36)\begin{align} \Delta_\phi \mathscr G & = \Delta \mathscr G -\langle \nabla \phi , \nabla \mathscr G \rangle = \Delta \mathscr G -\langle \nabla \phi , ( \mathscr G_x+e^f \mathscr G_w\nabla f) \rangle \nonumber\\ & =\Delta\mathscr G -\langle \nabla \phi, \mathscr G_x \rangle -e^f \mathscr G_w \langle \nabla \phi , \nabla f \rangle \\ & = \Delta_\phi \mathscr G^x + 2e^f \langle \mathscr G_{xw} ,\nabla f \rangle + e^f |\nabla f|^2 ( \mathscr G_w +e^f \mathscr G_{ww})+e^f \mathscr G_w \Delta_\phi f. \nonumber \end{align}

For the sake of future reference we also note that

(4.37)\begin{align} \Delta_\phi e^{{-}f} & = \Delta e^{{-}f} - \langle \nabla \phi , \nabla e^{{-}f} \rangle \nonumber\\ & ={-} {\rm div}(e^{{-}f}\nabla f)+e^{{-}f} \langle \nabla \phi, \nabla f \rangle \nonumber\\ & ={-}e^{{-}f} \Delta f + e^{{-}f} |\nabla f|^2 +e^{{-}f} \langle \nabla \phi , \nabla f \rangle ={-}e^{{-}f} (\Delta_\phi f - |\nabla f|^2). \end{align}

Returning to inequality (4.33) and picking up the estimate from where we left, for the last two terms about $\mathscr G$, we can write

(4.38)\begin{align} & 2 (\mu -1)\langle \nabla f,\nabla (e^{{-}f} \mathscr G) \rangle + \mu \Delta_\phi (e^{{-}f} \mathscr G) \nonumber\\ & \quad=2 (\mu -1) [ - e ^{{-}f} \mathscr G |\nabla f|^2 + e^{{-}f} \langle \nabla f, \nabla \mathscr G \rangle] \nonumber\\ & \qquad+\mu [ e^{{-}f} \Delta_\phi \mathscr G + \mathscr G \Delta_\phi e^{{-}f} -2 e^{{-}f} \langle \nabla f , \nabla \mathscr G \rangle] \nonumber\\ & \quad={-}2 (\mu -1) e ^{{-}f} \mathscr G |\nabla f|^2 + 2 \mu e^{{-}f} \langle \nabla f , \nabla \mathscr G \rangle \nonumber\\ & \qquad-2e^{{-}f} \langle \nabla f, ( \mathscr G_x + e^f \mathscr G_w \nabla f) \rangle + \mu e^{{-}f} ( \Delta_\phi \mathscr G^x +2e^f \langle \mathscr G_{xw} ,\nabla f \rangle) \nonumber\\ & \qquad+ \mu e^{{-}f} (e^f |\nabla f|^2 ( \mathscr G_w +e^f \mathscr G_{ww})+e^f \mathscr G_w \Delta_\phi f) \nonumber\\ & \qquad+ \mu \mathscr G e^{{-}f} ( -\Delta_\phi f+ |\nabla f|^2) -2 \mu e^{{-}f} \langle \nabla f , \nabla \mathscr G \rangle. \end{align}

As according to (4.10) we have

(4.39)\begin{align} [ \mu \mathscr G_w - \mu \mathscr G e^{{-}f}] \Delta_\phi f & = [{-}F^\mathscr G_\mathsf a/(\mu t_1) - (\mu -1) |\nabla f|^2/\mu] \left[ \mu(\mathscr G_w - \mathscr G e^{{-}f})\right] \nonumber\\ & ={-}(F^\mathscr G_\mathsf a/t_1) (\mathscr G_w -\mathscr G e^{{-}f}) -(\mu -1)|\nabla f|^2(\mathscr G_w -\mathscr G e^{{-}f}), \end{align}

upon substitution back in (4.38) this gives

\begin{align*} & 2 (\mu -1)\langle \nabla f,\nabla (e^{{-}f} \mathscr G) \rangle +\mu \Delta_\phi (e^{{-}f} \mathscr G) \nonumber\\ & \quad={-}2 (\mu -1) e^{{-}f} \mathscr G |\nabla f|^2 -2 e^{{-}f}\langle \nabla f, \mathscr G_x \rangle -2 \mathscr G_w |\nabla f|^2 \\ & \qquad+ \mu e^{{-}f} \Delta_\phi \mathscr G^x + 2 \mu \langle \mathscr G_{xw} ,\nabla f \rangle + \mu |\nabla f|^2 \mathscr G_w +\mu |\nabla f|^2 e^f\mathscr G_{ww} \\ & \qquad+ \mu \mathscr G e^{{-}f} |\nabla f|^2 - (F^\mathscr G_\mathsf a/t_1) (\mathscr G_w -\mathscr G e^{{-}f}) -(\mu -1)|\nabla f|^2(\mathscr G_w - \mathscr G e^{{-}f})\\ & \quad=|\nabla f|^2 [{-}2 (\mu -1) e^{{-}f} \mathscr G -2 \mathscr G_w + \mu \mathscr G_w + \mu e^f \mathscr G_{ww} ] \nonumber \\ & \qquad+ |\nabla f|^2 [ \mu e^{{-}f}\mathscr G -(\mu -1) \mathscr G_w + (\mu -1) \mathscr G e^{{-}f}] \nonumber \\ & \qquad- [2 \langle \nabla f , (e^{{-}f}\mathscr G_x -\mu \mathscr G_{xw})\rangle + (F^\mathscr G_\mathsf a/t_1) (\mathscr G_w -\mathscr G e^{{-}f}) -\mu e^{{-}f}\Delta_\phi \mathscr G^x]. \end{align*}

Therefore, by taking into account the relevant cancellations, after simplifying terms and using basic inequalities, we can write

(4.40)\begin{align} & 2 (\mu -1)\langle \nabla f, \nabla (e^{{-}f}\mathscr G) \rangle +\mu \Delta_\phi (e^{{-}f}\mathscr G)\nonumber\\ & \quad\ge|\nabla f|^2(e^{{-}f}\mathscr G - \mathscr G_w + \mu e^f\mathscr G_{ww}) - (F^\mathscr G_\mathsf a/t_1) (\mathscr G_w - e^{{-}f}\mathscr G)\nonumber\\ & \qquad-2 |\nabla f| |e^{{-}f} \mathscr G_x - \mu \mathscr G_{xw}|+\mu e^{{-}f} \Delta_\phi \mathscr G^x. \end{align}

As a result, making use of relations (4.34)–(4.37) and inequality (4.40), and substituting all back into (4.33) whilst making note of $|\langle \nabla f ,\, \nabla \mathsf a \rangle | \le |\nabla f| |\nabla \mathsf a|$ and the bound $0 \le \psi \le 1$ we obtain:

(4.41)\begin{align} 0 & \ge - \psi F^\mathscr G_\mathsf a ([c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2] t_1/R^2 +1+c_1 k^L t_1) \nonumber\\ & \quad-t_1 \psi^2 F^\mathscr G_\mathsf a (\mathscr G_w - e^{{-}f}\mathscr G) + t_1^2 (\psi ^2/m) [|\nabla f|^2 + e^{{-}f}\mathscr G +\mathsf a - \partial_t f]^2\nonumber\\ & \quad -2c_1 t_1 \psi ^{3/2} |\nabla f| F^\mathscr G_\mathsf a/R \nonumber\\ & \quad -2 t_1^2 \psi ^2 |\nabla f|^2 [(m-1)k +(\mu -1) k^U + k^\nabla - (e^{{-}f}\mathscr G-\mathscr G_w+\mu e^f \mathscr G_{ww})/2] \nonumber\\ & \quad-t_1 ^2 \psi ^2 |\nabla f| (2|e^{{-}f} \mathscr G_x -\mu \mathscr G_{xw}| + \mu |\nabla \partial_t \phi| + 2 \mu k^L |\nabla \phi|+2(\mu-1)|\nabla \mathsf a|) \nonumber\\ & \quad+\mu t_1^2 \psi^2 (e^{{-}f} \Delta_\phi \mathscr G^x+\Delta_\phi \mathsf a -\mu n [(k^L+k^U)^2+ 2 k^\nabla]). \end{align}

In order to derive the final bounds out of this inequality it is helpful to label by $y,\, z$ and $\mathsf {Y},\, \mathsf {Z}$ the quantities defined by (4.42) as appearing on the right-hand side of (4.41) and identify the latter in terms of the $\gamma$-quantities introduced earlier:

(4.42)\begin{equation} \begin{cases} y= \psi |\nabla f|^2, \\ z= \psi(\partial_t f -\mathsf a-e^{{-}f}\mathscr G), \\ y-\mu z= \psi F^\mathscr G_\mathsf a/t_1>0, \\ \mathsf{Y} = 2[(m-1)k +(\mu -1) k^U + k^\nabla] \\ \qquad + \sup \{[{-}e^{{-}f}\mathscr G + \mathscr G_w - \mu e^f \mathscr G_{ww}]_+ : (t,x,w) \in Q_{2R, T}\} \\ \quad = 2[(m-1)k +(\mu -1) k^U + k^\nabla] + \gamma^{{\mathscr G}, \mu}_\mathsf{A} (2R), \\ \mathsf{Z} = \mu \ell_2 + 2 \mu k^L \ell_1 + 2\sup \{|e^{{-}f} \mathscr G_x - \mu \mathscr G_{xw}| : (t,x,w) \in Q_{2R, T}\} \\ \qquad +2( \mu -1) \sup \{ |\nabla \mathsf a| : (x,t) \in Q_{2R, T}\} \\ \quad = \mu \ell_2 + 2 \mu k^L \ell_1 + 2 \gamma^{{\mathscr G}, \mu}_{\mathsf B}(2R) + 2 \gamma^{\mathsf aw, \mu}_{\mathsf B}(2R). \end{cases} \end{equation}

By substituting these back into (4.41) it follows from basic considerations that,

(4.43)\begin{align} 0 & \ge-\psi F^\mathscr G_\mathsf a ([c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2] t_1/R^2 +1+c_1 k^L t_1) \nonumber\\ & \quad+ (t_1 ^2/m) [(y-z)^2 - (2mc_1/R) \sqrt y (y-\mu z)-m\mathsf{Y}y -m\mathsf{Z} \sqrt y] \\ & \quad-t_1 \psi F^\mathscr G_\mathsf a [\mathscr G_w - e^{{-}f}\mathscr G]_+{+} \mu t_1 ^2 \psi ^2 [ e^{{-}f} \Delta_\phi \mathscr G^x+\Delta_\phi \mathsf a]_- \nonumber\\ & \quad- \mu t_1 ^2 \psi ^2 [\mu n (k^L+k^U)^2 + 2 \mu n k^\nabla]. \nonumber \end{align}

Moreover, by an application of the Cauchy–Schwartz and Young's inequalities, it is seen that for any $\varepsilon \in (0,\,1)$, we have

(4.44)\begin{align} & (y-z)^2 - (2\,m c_1/R) \sqrt y (y-\mu z) - m\mathsf{Y} y -m\mathsf{Z} \sqrt y \nonumber\\ & \quad\ge (y-\mu z)^2/\mu^2 - m^2c_1^2 \mu^2 (y-\mu z)/[2(\mu-1)R^2] \nonumber\\ & \qquad- m^2 \mu^2 \mathsf{Y}^2 /[4(1-\varepsilon)(\mu-1)^2] -(3/4) (m^4 \mu^2 \mathsf{Z}^4/[4 \varepsilon(\mu-1)^2])^{1/3}. \end{align}

Hence by taking advantage of (4.44) it follows from (4.43) that

(4.45)\begin{align} 0 & \ge- \psi F^\mathscr G_\mathsf a ([c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2] t_1/R^2 +1+c_1 k^L t_1) \nonumber\\ & \quad+ (t_1^2/m) [(\psi F^\mathscr G_\mathsf a)^2/(t_1^2 \mu ^2) - m^2 c_1 ^2 \mu^2 (\psi F^\mathscr G_\mathsf a) / (2(\mu -1)R^2 t_1)] \nonumber\\ & \quad-(mt_1^2\mu^2 \mathsf{Y}^2) /[4(1-\varepsilon)(\mu-1)^2] -t_1 \psi F^\mathscr G_\mathsf a [\mathscr G_w - e^{{-}f}\mathscr G]_+ \nonumber\\ & \quad -[(3t_1^2)/(4m)] (m^4 \mu^2 \mathsf{Z}^4/[4 \varepsilon(\mu-1)^2])^{1/3} \nonumber\\ & \quad+ \mu t_1 ^2 \psi ^2 [ e^{{-}f} \Delta_\phi \mathscr G^x+\Delta_\phi \mathsf a ]_-- \mu t_1 ^2 \psi ^2 [\mu n (k^L+k^U)^2 + 2 \mu n k^\nabla]. \end{align}

Subsequently and more shortly we can deduce and write the above inequality as a quadratic inequality

(4.46)\begin{equation} 0 \ge (\psi F^\mathscr G_\mathsf a)^2/(m\mu^2) - (\psi F^\mathscr G_\mathsf a) \mathsf{X}_1 - t_1^2 \mathsf{X}_2, \end{equation}

where we have set

(4.47)\begin{align} \mathsf{X}_1 & = [c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2]t_1/R^2 +1 \nonumber\\ & \quad+ c_1 k^L t_1 + m t_1 c_1 ^2 \mu ^2/[2(\mu -1)R^2] +t_1\gamma^\mathscr G_{\mathsf C}(2R), \end{align}

and

(4.48)\begin{align} \mathsf{X}_2& =m \mu^2 \mathsf{Y}^2/[4(1-\varepsilon)(\mu-1)^2] \nonumber\\ & \quad+ (3/4) [ m \mu^2 \mathsf{Z}^4/(4 \varepsilon(\mu-1)^2) ]^{1/3} \nonumber\\ & \quad+ \mu ^2 n (k^L+k^U)^2 + 2 \mu^2 n k^\nabla + \mu ( \gamma^\mathscr G_{\mathsf D}(2R)+\gamma^{\mathsf aw}_{\mathsf D}(2R)), \end{align}

whilst making note of (2.7), (2.8) and (2.10) (with $2R$ replacing $R$). As a result it follows from (4.46) that

(4.49)\begin{align} \psi F^\mathscr G_\mathsf a & \le (m \mu^2/2) \left( \mathsf{X}_1 + \sqrt{\mathsf{X}_1^2+ (4 t^2_1 \mathsf{X}_2/)(m\mu^2)} \right) \nonumber\\ & \le (m \mu^2/2) \left( 2\mathsf{X}_1+\sqrt{(4t_1^2 \mathsf{X}_2)/(m \mu^2)} \right) = m \mu^2\mathsf{X}_1 +t_1 \mu \sqrt{m\mathsf{X}_2}. \end{align}

Since $\psi \equiv 1$ for $r(x,\, \tau ) \le R$ and $(x_1,\, t_1)$ is the point where $\psi F^\mathscr G_\mathsf a$ attains its maximum on $\{r(x,\, t) \le 2R,\, 0 \le t \le \tau \}$ we have from (4.49) the bound

(4.50)\begin{equation} F^\mathscr G_\mathsf a(x, \tau) = [\psi F^\mathscr G_\mathsf a] (x, \tau) \le [\psi F^\mathscr G_\mathsf a] (x_1,t_1) \le m \mu^2\mathsf{X}_1 +t_1 \mu \sqrt{m\mathsf{X}_2}.\end{equation}

Therefore, recalling (4.7), substituting for $\mathsf {X}_1$ and $\mathsf {X}_2$ from (4.47) and (4.48) respectively and making note of  $t_1 \le \tau$, we can write after dividing both sides by $\mu \tau >0$,

(4.51)\begin{align} \mu^{{-}1} |\nabla f|^2 - \partial_t f +\mathsf a(x,t)+ e^{{-}f} \mathscr G & \le~(m \mu/\tau) \mathsf{X}_1 + \sqrt{m \mathsf{X}_2} \nonumber\\ & \le~(m \mu) [c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2] /R^2 \nonumber\\ & \quad+ (m \mu/\tau) + (m \mu) (\gamma^\mathscr G_{\mathsf C}(2R) + c_1 k^L \nonumber\\ & \quad+ m c_1 ^2 \mu ^2/[2(\mu -1)R^2]) \nonumber\\ & \quad+ \sqrt m \{ m \mu^2 \mathsf{Y}^2/[4(1-\varepsilon)(\mu-1)^2] \nonumber\\ & \quad+ (3/4) [ m \mu^2 \mathsf{Z}^4/(4 \varepsilon(\mu-1)^2) ]^{1/3} \\ & \quad+ n\mu^2 (k^L+k^U)^2 + 2n \mu^2 k^\nabla \nonumber\\ & \quad+\mu (\gamma^\mathscr G_{\mathsf D}(2R)+\gamma^{\mathsf aw}_{\mathsf D}(2R) \}^{1/2}. \nonumber \end{align}

Finally using the arbitrariness of $0< \tau \le T$ it follows after reverting back to $w$ upon noting the relation $f=\log w$ and rearranging terms that

(4.52)\begin{align} \frac{|\nabla w|^2}{\mu w^2} - \frac{\partial_t w}{w} + \frac{\mathscr G}{w}+\mathsf a(x,t) & \le (m \mu) [1/t +\gamma^\mathscr G_{\mathsf C}(2R) + c_1 k^L] \nonumber\\ & \quad+ (m \mu) [m c_1 ^2 \mu ^2/[2(\mu -1)]+c_2 \nonumber\\ & \quad+(m-1) c_1(1+R \sqrt{k})+2c_1^2]/R^2 \nonumber\\ & \quad+ \sqrt m \{ m \mu^2 \mathsf{Y}^2/[4(1-\varepsilon)(\mu-1)^2]\nonumber\\ & \quad+ (3/4) [ m \mu^2 \mathsf{Z}^4/(4 \varepsilon(\mu-1)^2) ]^{1/3} \nonumber\\ & \quad+ n\mu^2 (k^L+k^U)^2 + 2n \mu^2 k^\nabla \nonumber\\ & \quad+ \mu [\gamma^\mathscr G_{\mathsf D}(2R)+\gamma^{\mathsf aw}_{\mathsf D}(2R)] \}^{1/2}. \end{align}

A reference to (4.42) and substituting for ${\mathsf Y}$, ${\mathsf Z}$ leads at once to the desired estimate as formulated in theorem 4.1.

The global version of the above estimate can now be obtained by imposing suitable global bounds and then passing to the limit $R \to \infty$ on the right-hand side.

Theorem 4.5 Let $(M,\, g,\, d\sigma )$ be a smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and assume that the metric-potential pair $(g,\, \phi )$ is time dependent and of class $\mathscr {C}^2$. Assume ${\mathscr Ric}^m_\phi (g) \ge -(m-1) k g$ and (4.2)–(4.3) hold globally in $M \times [0,\, T]$. Let $w=w(x,\,t)$ be a positive solution to (1.1). Then for every $\mu >1$, $\varepsilon \in (0,\, 1)$ and for all $x \in M$, $0< t \le T$ we have the global gradient estimate

(4.53)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} - \frac{\partial_t w}{w} + \frac{\mathscr G(t,x,w)}{w} +\mathsf a(x,t) \le m \mu \left[ \frac{1}{t} + c_1 k^L + \gamma^\mathscr G_{\mathsf C} \right] + \mathsf{M}_\mathsf a^\mathscr G, \end{equation}

where $\gamma ^\mathscr G_{\mathsf C}$ is as in (2.7) and

(4.54)\begin{align} \mathsf{M}_\mathsf a^\mathscr G & =\sqrt m \bigg\{n\mu ^2 (k^L + k^U)^2 + 2n \mu^2 k^\nabla + \mu \gamma^{\mathscr G}_{\mathsf D} + \mu \gamma^{\mathsf aw}_{\mathsf D} \nonumber\\ & \quad+ \frac{m \mu^2 [(m-1) k +(\mu -1) k^U + k^\nabla + \gamma^{{\mathscr G}, \mu}_\mathsf{A}/2]^2}{(1-\varepsilon)(\mu-1)^2}\nonumber\\ & \quad+ \left. \frac{3}{4} \left[ \frac{m \mu^2 [\mu \ell_2 + 2 \mu k^L \ell_1+ 2\gamma^{{\mathscr G}, \mu}_\mathsf{B} + 2\gamma^{\mathsf aw, \mu}_\mathsf{B}]^4}{4 \varepsilon(\mu-1)^2} \right]^{1/3} \right\}^{1/2}. \end{align}

With the aid of the differential Harnack estimate established in theorem 4.1 we can now prove a parabolic Harnack inequality for positive solutions to the system (1.1).

Theorem 4.6 Under the assumptions of theorem 4.1 for all $(x_1,\, t_1)$, $(x_2,\, t_2)$ in $Q_{R, T}$ with $t_2>t_1$ and $\mu >1$ we have

(4.55)\begin{equation} w(x_2,t_2) \ge w(x_1,t_1) \left(\frac{t_2}{t_1}\right)^{{-}m \mu} {\rm exp} \left[ \Sigma (t_2-t_1) - \frac{\mu L(x_1,x_2)}{4(t_2-t_1)} \right]. \end{equation}

Here $L(x_1,\,x_2) = \inf ||\,|\dot \zeta (t)|_{g(t)}^2 ||_{L^1(0,1; {\rm d}t)}$ where the infimum is over all $\zeta \in \mathscr {C}^1( [0,\, 1]; M)$ lying in $Q_{R, T}$ with $\zeta (0) = x_1$, $\zeta (1) = x_2$ and the constant $\Sigma$ depends only on the bounds in theorem 4.1 $[$see (4.57)–(4.58) $]$. If the bounds as in theorem 4.5 are global then the estimate is global.

Proof. Here we shall focus only on the local Harnack inequality as the global one is very similar. The idea is to integrate estimate (4.4) along suitable space–time curves in $Q_{R,T} \subset M \times [0,\, T]$. To this end let us first rewrite the latter inequality (4.4) as

(4.56)\begin{equation} \frac{\partial_t w}{w} \ge \frac{|\nabla w|^2}{\mu w^2} - \frac{m \mu}{t} + \Sigma. \end{equation}

Here $\Sigma$ is a constant containing all the terms (bounds) on the right-hand side of (4.4) except the first, and the terms $\underline {\mathsf a}$, $\underline {\mathscr G}$ resulting from the expression on the left, specifically,

(4.57)\begin{align} \Sigma & = \underline{\mathscr G} + \underline{\mathsf a} - (m \mu c_1 k^L+\mathsf{L}+m \mu\gamma^{\mathscr G}_{\mathsf C} (2R)+\mathsf{M}_\mathsf a^\mathscr G), \end{align}

(4.58)\begin{align} \underline {\mathsf a} & = \inf_{Q_{2R,T}} {\mathsf a}, \qquad \underline {\mathscr G} = \inf_{\Theta_{2R,T}} \mathscr G(t,x,w)/w. \end{align}

Suppose $\zeta \in \mathscr {C}^1( [t_1,\,t_2]; M)$ is an arbitrary curve lying entirely in $Q_{R, T}$ with ${\zeta (t_1) = x_1}$ and $\zeta (t_2) = x_2$. Using the above inequality and writing $\dot \zeta = d\zeta /{\rm d}t$ it is seen that

(4.59)\begin{align} d/{\rm d}t [\log w(\zeta(t),t)] & = \langle \nabla w/w, \dot \zeta (t) \rangle + \partial_t w/w \nonumber\\ & \ge \langle \nabla w/w, \dot \zeta (t) \rangle + |\nabla w|^2/(\mu w^2) - ( m \mu)/t + \Sigma \nonumber\\ & = \mu^{{-}1} |\nabla w/w + \mu \dot \zeta (t)/2|^2 - \mu |\dot \zeta (t)|^2/4 - (m \mu)/t + \Sigma \nonumber\\ & \ge -\mu |\dot \zeta (t)|^2/4 - (m \mu)/t + \Sigma, \end{align}

where the inner products are with respect to the metric $g(t)$. Integrating the above inequality thus gives

(4.60)\begin{align} \log \frac{w(x_2,t_2)}{w(x_1,t_1)} & = \log w(\zeta(t),t)\bigg|_{t_1}^{t_2} = \int_{t_1}^{t_2} \frac{d}{{\rm d}t} \log w(\zeta(t),t) \, {\rm d}t \nonumber\\ & \ge \int_{t_1}^{t_2} -\frac{\mu}{4} |\dot \zeta (t)|^2 \,{\rm d}t - \int_{t_1}^{t_2} \frac{m \mu}{t} {\rm d}t+\int_{t_1}^{t_2} \Sigma \, {\rm d}t \nonumber\\ & ={-}m \mu \log (t_2/t_1) - (\mu/4) \int_{t_1}^{t_2} |\dot \zeta (t)|^2 \,{\rm d}t + (t_2-t_1) \Sigma. \end{align}

Reparametrizing the curve $\zeta$ and exponentiating both sides gives at once (4.55).

5. The case of time-independent metrics and potentials

In this section we discuss gradient estimates and the implications of what has been developed earlier in the so-called static case, that is, when the metric and potential are time independent ($\partial _t g \equiv 0$ and $\partial _t \phi \equiv 0$). The local and global differential Harnack estimates for positive smooth solutions to the equation

(5.1)\begin{equation} {\mathscr L}_\phi^{\mathsf a} [w] = (\partial_t-\mathsf{a}(x,t)-\Delta_\phi) w = \mathscr G(t,x,w), \end{equation}

can be formulated as below. Note that in this context $Q_{R,T} = {\mathscr B}_{R} \times [0,\, T]$ with $R,\, T>0$ and the explicit bounds (4.2)–(4.3) are no longer needed (see the proof below).

Theorem 5.1 Let $(M,\, g,\, d\sigma )$ be a smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and let ${\mathscr Ric}_\phi ^m(g) \ge -(m-1) k g$ in $\mathscr {B}_{2R}$ for some $m \ge n$, $k \ge 0$ and $R>0$. If $w=w(x,\,t)$ is a positive solution to (5.1), then for every $\mu >1$, $\varepsilon \in (0,\, 1)$ and for all $(x,\,t)$ in ${\mathscr B}_{R} \times [0,\, T]$ with $t>0$ we have the gradient estimate

(5.2)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} - \frac{\partial_t w}{w} + \frac{\mathscr G(t,x,w)}{w} + {\mathsf a}(x,t) \le \frac{m \mu}{t} + \mathsf{L} +m \mu \gamma^\mathscr G_{\mathsf C}(2R) + \mathsf{M}_{\mathsf a}^\mathscr G. \end{equation}

The quantities appearing on the right-hand side of the bound (5.2) are given respectively by

(5.3)\begin{equation} \mathsf{L} = \frac{m\mu}{R^2}\left[ \frac{m c_1 ^2 \mu ^2}{2(\mu -1)}+c_2 +(m-1) c_1(1+R \sqrt{k})+2c_1^2 \right] \end{equation}

and

(5.4)\begin{align} \mathsf{M}_{\mathsf a}^\mathscr G & =\sqrt m \left\{ \mu [\gamma^\mathscr G_{\mathsf D}(2R)+\gamma^{\mathsf aw}_{\mathsf D}(2R)] + \frac{m \mu^2 [(m-1)k + \gamma^{\mathscr G, \mu}_{\mathsf A} (2R)/2]^2}{(1-\varepsilon)(\mu-1)^2} \right. \nonumber\\ & \quad+ \left. \frac{3}{4} \left[ \frac{4\,m \mu^2 [\gamma^{\mathscr G, \mu}_{\mathsf B} (2R) + \gamma^{\mathsf aw, \mu}_{\mathsf B} (2R)]^4}{\varepsilon(\mu-1)^2} \right]^{1/3} \right\}^{1/2}. \end{align}

Proof. Referring to theorem 4.1 and bounds (4.2)–(4.3) we can set $k^L=0$, $k^U=0$, $k^\nabla =0$ and $\ell _2=0$. Substituting these values in (4.5)–(4.6) leads to (5.3)–(5.4). Note that here in the formulation of $\mathsf {M}^\mathsf a_\mathscr G$ we have observed that in (4.42) in the expression for $\mathsf {Y}$ we have $(\mu -1) k^U + k^\nabla =0$ and in the expression for $\mathsf {Z}$ we have $\mu \ell _2 + 2 \mu k^L \ell _1 =0$. The resulting cancellations lead to (5.4).

Theorem 5.2 Let $(M,\, g,\, d\sigma )$ be a smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and ${\mathscr Ric}_\phi ^m(g) \ge -(m-1) k g$ in $M$ for some $m\ge n$ and $k \ge 0$. If $w=w(x,\,t)$ is a positive solution to (5.1), then for every $\mu >1$, $\varepsilon \in (0,\, 1)$ and for all $(x,\,t)$ in $M \times [0,\, T]$ with $t>0$ we have the global gradient estimate

(5.5)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} - \frac{\partial_t w}{w} + \frac{\mathscr G(t,x,w)}{w} + {\mathsf a} (x,t) \le \frac{m \mu}{t} + m\mu \gamma^\mathscr G_{\mathsf C} + \mathsf{M}_\mathsf a^\mathscr G, \end{equation}

where

(5.6)\begin{align} \mathsf{M}_\mathsf a^\mathscr G & =\sqrt m \left\{ \mu (\gamma^\mathscr G_{\mathsf D} + \gamma^{{\mathsf a} w}_{\mathsf D}) + \frac{m \mu^2 [(m-1)k + \gamma^{\mathscr G, \mu}_{\mathsf A}/2]^2}{(1-\varepsilon)(\mu-1)^2}\right.\nonumber\\ & \quad + \left.\frac{3}{4} \left[ \frac{4\,m \mu^2 [\gamma^{\mathscr G, \mu}_{\mathsf B} + \gamma^{{\mathsf a} w, \mu}_{\mathsf B}]^4}{\varepsilon(\mu-1)^2} \right]^{1/3} \right\}^{1/2} \end{align}

and the $\gamma$-quantities used are as in (2.5)–(2.8).

Proof. Starting from (5.2) and the terms on the right, an inspection of (5.3) shows that $\mathsf {L}\to 0$ as $R \to \infty$. A similar consideration for expression (5.6) shows that it suffices to replace the local constants $\gamma ^{\mathscr G, \mu }_{\mathsf A}(2R)$, $\gamma ^{\mathscr G, \mu }_{\mathsf B}(2R)$, $\gamma ^\mathscr G_{\mathsf C}(2R)$, $\gamma ^\mathscr G_{\mathsf D}(2R)$ and $\gamma ^{\mathsf aw}_{\mathsf D}(2R)$, $\gamma ^{{\mathsf a} w,\, \mu }_{\mathsf B}(2R)$ with their global counterparts. The conclusion now follows by passing to the limit $R \to \infty$ in (5.2) and taking the above into account.

In the static case and for the elliptic counterpart of (5.1) ($\partial _t g \equiv 0$, $\partial _t \phi \equiv 0$, $\partial _t w \equiv 0$, $\partial _t {\mathsf a} \equiv 0$) we can deduce from the above global estimate by passing to the limit $t \to \infty$ the following global elliptic estimate

(5.7)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} + \frac{\mathscr G(x,w)}{w} + {\mathsf a} (x) \le m \mu \gamma^\mathscr G_{\mathsf C} + \mathsf{M}_{\mathsf a}^\mathscr G. \end{equation}

As a consequence of the global elliptic estimate (5.7) we can now prove the following Liouville type result for positive solutions to the equation $\Delta _\phi w + \mathscr G(w) =0$ [i.e., ${\mathsf a} \equiv 0$ and $\mathscr G=\mathscr G(w)$]. We later present some applications to specific nonlinearities.

Theorem 5.3 Let $(M,\, g,\, d\sigma )$ be a smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and ${\mathscr Ric}_\phi ^m(g) \!\ge 0$ everywhere in $M$. Let $w$ be a positive solution to $\Delta _ \phi w \!+ \mathscr G(w) = 0$. Then for every $\mu >1$, $\varepsilon \in (0,\, 1)$ and all $x \in M$ we have the global gradient estimate

(5.8)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} + \frac{\mathscr G(w)}{w} \le \frac{m \mu \gamma^{{\mathscr G}, \mu}_\mathsf{A}}{2(\mu-1) \sqrt{1-\varepsilon}} + m \mu \gamma^{\mathscr G}_\mathsf{C}. \end{equation}

In particular, if along the solution $w$, we have the following

• • $\mathscr G(w) \ge 0$,

• • $\mathscr G(w) - w \mathscr G'(w) \ge 0$,

• • $\mathscr G(w)-w\mathscr G'(w)+\mu w^2 \mathscr G''(w) \ge 0$ for some $\mu >1$,

everywhere on $M$, then $w$ is constant and as a result $\mathscr G(w)=0$.

Proof. Since $\mathscr G=\mathscr G(w)$ and ${\mathsf a} \equiv 0$ we obtain from (2.4), (2.8) the identities $\gamma ^\mathscr G_{\mathsf D} =0$, $\gamma ^{{\mathsf a} w}_{\mathsf D}=0$ and from (2.2), (2.6) the identities $\gamma ^{\mathscr G, \mu }_{\mathsf B} =0$, $\gamma ^{{\mathsf a} w,\, \mu }_{\mathsf B}=0$. Hence substituting these together with $k=0$ in (5.7) we arrive at once at (5.8). Next, from the prescribed inequalities satisfied by ${\mathscr G}$ we have

(5.9)\begin{equation} \gamma^{{\mathscr G}, \mu}_\mathsf{A} = \sup_{M} \mathsf{A}_{\mathscr G}^\mu (w) = \sup_{M} \left\{ \frac{1}{w}[-\mathscr G(w) + w\mathscr G'(w) - \mu w^2 \mathscr G''(w)]_+ \right\} =0 \end{equation}

and in a similar way

(5.10)\begin{equation} \gamma^\mathscr G_{\mathsf C} = \sup_{M} \mathsf{C}_{\mathscr G}(w) = \sup_{M} \left\{ \frac{1}{w} [ w \mathscr G' (w) - \mathscr G(w) ]_+ \right\} =0.\end{equation}

Thus substituting back into (5.8) it follows that

(5.11)\begin{equation} \frac{|\nabla w|^2}{\mu w^2} \le \frac{|\nabla w|^2}{\mu w^2} + \frac{\mathscr G(w)}{w} \equiv 0\end{equation}

and so $|\nabla w| \equiv 0$. Therefore, $u$ is a constant and so a further reference to the equation $\Delta _\phi w + \mathscr G(w) = 0$ gives $\mathscr G(w)=0$.

In order to illustrate the strength of the Liouville result in theorem 5.3 let us turn to considering some specific cases. As a first application consider the nonlinearity

(5.12)\begin{equation} \mathscr G(w) = \sum_{j=1}^d \mathsf{A}_j w^{p_j}, \end{equation}

with real coefficients $\mathsf {A}_j$ and real exponents $p_j$ ($1 \le j \le d$). Then by a direct calculation $\mathscr G - w \mathscr G' = \sum \mathsf {A}_j (1-p_j) w^{p_j}$ and $\mathscr G - w \mathscr G' + \mu w^2 \mathscr G' = \sum [\mathsf {A}_j (p_j -1) (\mu p_j -1)] w^{p_j}$. If $\mathsf {A}_j \ge 0$ we have $\mathscr G(w) \ge 0$ whilst if $p_j \le 1$ we have $\mathscr G -w\mathscr G' \ge 0$ and so $\mathscr G-w \mathscr G' + \mu w^2 \mathscr G'' \ge 0$ (by choosing $\mu >1$ suitably). Hence theorem 5.3 now leads to the following conclusion extending earlier results on Yamabe type problems to more general nonlinearities.

Theorem 5.4 Let $(M,\, g,\, d\sigma )$ be a complete smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and ${\mathscr Ric}^m_\phi (g) \ge 0$. Let $w$ be a positive smooth solution to the equation

(5.13)\begin{equation} \Delta_\phi w + \sum_{j=1}^d \mathsf{A}_j w^{p_j} = 0. \end{equation}

If $\mathsf {A}_j \ge 0$ and $p_j \le 1$ for $1 \le j \le d$ then $w$ is a constant.

As another application relating to the discussions in § 1 consider a nonlinearity $\mathscr G = \mathscr G(w)$ in the form of a superposition of logarithmic and power-like nonlinearities, with real coefficients $\mathsf {A},\, \mathsf {B}$, real exponents $p$, $q$, and a function $\Phi \in \mathscr {C}^2(\mathbb {R})$, specifically, in the form

(5.14)\begin{equation} \mathscr G(w) = \mathsf{A} w^p \Phi(\log w) + \mathsf{B} w^q. \end{equation}

A straightforward calculation pertaining to the quantities formulated in theorem 5.3 now leads to

(5.15)\begin{equation} {\mathscr G} - w {\mathscr G}' = \mathsf{A} w^p [(1-p)\Phi - \Phi'] + \mathsf{B} (1-q) w^q, \end{equation}

and subsequently

(5.16)\begin{align} {\mathscr G} - w {\mathscr G}' + \mu w^2 {\mathscr G}' & =~{\mathsf A} (1-p)(1-\mu p) w^p \Phi + {\mathsf A} [\mu (2p-1)-1] w^p \Phi' \nonumber\\ & \quad+ {\mathsf A} \mu w^p \Phi' + \mathsf{B} (q -1) (\mu q -1) w^q, \end{align}

where the argument $s=\log w$ of $\Phi$ and its derivatives have been abbreviated. Next let us formally fix an upper and a lower bound on the solutions $w$, say, $0<\underline w \le w \le \overline w$ and put $\alpha =\log \underline w$, $\beta = \log \overline w$. Then evidently $s=\log w \in [\alpha,\, \beta ] \subset (0,\, \infty )$. Furthermore, suppose $\Phi >0$ and let $c^L$, $c^U$ denote the infimum and supremum of $\Phi '/\Phi$ and $d$ the infimum of $\Phi ''/\Phi$ over $[\alpha,\, \beta ]$ respectively. Then it is clear that we have the inequalities

(5.17)\begin{equation} c^L \le \Phi'/\Phi \le c^U, \qquad \Phi''/\Phi \ge d. \end{equation}

Next, regarding the condition ${\mathscr G} - w {\mathscr G}' \ge 0$ in theorem 5.3, we have upon noting (5.15) the implications ${\mathscr G} - w {\mathscr G}' \ge 0 \iff (1-p) \Phi \ge \Phi ' \iff 1-p \ge \Phi '/\Phi$ which then holds when

(5.18)\begin{equation} 1-p \ge c^U. \end{equation}

Likewise regarding the condition ${\mathscr G} - w {\mathscr G}' + \mu w^2 {\mathscr G}' \ge 0$ in theorem 5.3 we have upon referring to (5.16) the relation $(1-p)(1-\mu p) + [\mu (2p-1)-1] \Phi '/\Phi + \mu \Phi ''/\Phi \ge 0$ which by taking advantage of (5.17) holds when

(5.19)\begin{align} & (1-p)(1-\mu p) + [\mu(2p-1)-1] c^L + \mu d \ge 0\text{ if }(2p-1)\mu-1 \ge 0, \end{align}

(5.20)\begin{align} & (1-p)(1-\mu p) + [\mu(2p-1)-1] c^U + \mu d \ge 0\text{ if }(2p-1)\mu-1 \le 0. \end{align}

The following theorem now directly results from theorem 5.3.

Theorem 5.5 Let $(M,\, g,\, d\sigma )$ be a complete smooth metric measure space with $d\sigma =e^{-\phi } dv_g$ and ${\mathscr Ric}^m_\phi (g) \ge 0$. Let $w$ be a positive smooth solution to the equation

(5.21)\begin{equation} \Delta_\phi w + \mathsf{A} w^p \Phi(\log w) + \mathsf{B} w^q = 0. \end{equation}

where $\Phi \in \mathscr {C}^2(\mathbb {R})$ is as described above. Assume $\mathsf {A},\, \mathsf {B} \ge 0$, $q \le 1$ and $p \in {\mathbb {R}}$ satisfies (5.18) and (5.19)–(5.20) for some $\mu >1$ $($with $1<\mu <1/q$ when ${\mathsf B} \neq 0$ and $0< q<1 )$. Then $w$ is a constant. Moreover $\mathsf {A} w^p \Phi (\log w) + \mathsf {B} w^q=0$.

It is interesting to note that in the case $p=1$ the above follows from $\Phi \ge 0$, $\Phi ' \le 0$ and $\mu \Phi ''+(\mu -1)\Phi '\ge 0$ for some $\mu >1$ (or $1<\mu <1/q$ if ${\mathsf B} \neq 0$ and $0< q<1$).

6. Further global bounds under super Perelman–Ricci flow

In this section we establish a different type of gradient estimate for positive smooth solutions to system (1.1). In fact, here, we establish the estimate under a weaker form of the flow inequality (i.e., corresponding to the case $m=\infty$) by assuming that the metric and potential evolve under a ${\mathsf k}$-super Perelman–Ricci flow:

(6.1)\begin{equation} \begin{cases} \dfrac{1}{2} \dfrac{\partial g}{\partial t} (x,t) + {\mathscr Ric}_\phi(g)(x,t) \ge - \mathsf{k}g(x,t), \qquad {\mathsf k} \ge 0,\\ {\mathscr Ric}_\phi(g)(x,t) = {\mathscr Ric} (g)(x,t) + \nabla_{g(t)} \nabla_{g(t)} \phi (x,t). \end{cases} \end{equation}

To this end suppose that $w=w(x,\,t)$ is a positive smooth solution to the equation ${\mathscr L}_\phi ^{\mathsf a} (w) = [\partial _t -{\mathsf a}(x,\,t)- \Delta _\phi ] w = \mathscr G(t,\,x,\,w)$. For $p \ge 2$, $q \in \mathbb {R}$ a pair of exponents and $\zeta =\zeta (t)$ a non-negative, smooth but otherwise arbitrary function set

(6.2)\begin{equation} {\bf X}^{p,q}_\zeta[w] = \zeta(t) \frac{|\nabla w|^p}{w^q} + \Gamma(w), \end{equation}

where $\Gamma =\Gamma (w)$ with $w>0$ is some given function of class $\mathscr {C}^2$.

Lemma 6.1 For $p \ge 2$, $q \in {\mathbb {R}}$, $\zeta =\zeta (t)$ as above and ${\mathscr L}_\phi ^{\mathsf a}$ as in (1.3), ${\bf X}^{p, q}_\zeta [w]$ satisfies the evolution identity

(6.3)\begin{align} {\mathscr L}_\phi^{\mathsf a} ({\bf X}^{p, q}_\zeta [w])& = \zeta' \frac{|\nabla w|^p}{w^q} - p \zeta \frac{|\nabla w|^{p-2}}{w^q} \left[ \frac{1}{2} \partial_t g + {\mathscr Ric}_\phi \right] (\nabla w, \nabla w) \nonumber\\ & \quad+p \zeta \frac{|\nabla w|^{p-2}}{w^q} \bigg[ \mathsf a |\nabla w|^2 + w \langle \nabla w, \nabla \mathsf a \rangle + \mathscr G_w |\nabla w|^2 + \langle \nabla w, \mathscr G_x \rangle \bigg]\nonumber\\ & \quad-q\zeta [\mathsf a w +\mathscr G] \frac{|\nabla w|^p}{w^{q+1}} - \zeta \mathsf a \frac{|\nabla w|^p}{w^q} - \frac{p}{2} \frac{\zeta}{w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle \nonumber\\ & \quad- p \zeta \frac{|\nabla w|^{p-2}}{w^q} \left| \nabla \nabla w - \frac{q}{w} [\nabla w \otimes \nabla w] \right|^2 - q[q+1-pq] \zeta \frac{|\nabla w|^{p+2}}{w^{q+2}} \nonumber\\ & \quad- \mathsf a \Gamma(w) + (\mathsf aw+\mathscr G) \Gamma'(w) - \Gamma''(w) |\nabla w|^2. \end{align}

In particular if the metric-potential pair evolves under the super Perelman–Ricci flow inequality (6.1) then

(6.4)\begin{align} {\mathscr L}_\phi^{\mathsf a} ({\bf X}^{p,q}_\zeta[w]) & \le \frac{|\nabla w|^p}{w^q} \left[ \zeta' + p \zeta (\mathsf{k} +\mathsf a+ \mathscr G_w) - (q+1) \zeta \mathsf a - q \zeta \frac{\mathscr G}{w} \right] \nonumber\\ & \quad+ p \zeta \frac{|\nabla w|^{p-1}}{w^q} (|\nabla \mathsf a|w+ |\mathscr G_x|) - q[q+1-pq] \zeta \frac{|\nabla w|^{p+2}}{w^{q+2}}\nonumber\\ & \quad- \mathsf a \Gamma(w) + (\mathsf aw+\mathscr G) \Gamma'(w) - \Gamma''(w) |\nabla w|^2. \end{align}

Proof. The application of the operator ${\mathscr L}_\phi ^{\mathsf a} = \partial _t -{\mathsf a}(x,\,t)- \Delta _\phi$ on (6.2) is easily seen to split into the sum

(6.5)\begin{equation} {\mathscr L}_\phi^{\mathsf a} ({\bf X}^{p,q}_\zeta[w]) = \zeta' |\nabla w|^p/w^q + \zeta {\mathscr L}_\phi^{\mathsf a} (|\nabla w|^p/w^q) + {\mathscr L}_\phi^{\mathsf a} (\Gamma(w)). \end{equation}

Starting from the last term on the right-hand side it is not difficult to see that

(6.6)\begin{equation} {\mathscr L}_\phi^{\mathsf a} (\Gamma(w)) = \Gamma'(w) {\mathscr L}_\phi^{\mathsf a}(w) - {\mathsf a} [\Gamma(w) - w \Gamma'(w)] - \Gamma''(w) |\nabla w|^2.\end{equation}

Moving onto the second term which is the more involved one we proceed by calculating the first order space–time derivatives of $|\nabla w|^p/w^q$ as

(6.7)\begin{equation} \left[\begin{array}{@{}c@{}} \partial_t \\ \nabla \end{array}\right] \frac{|\nabla w|^p}{w^q} = p\frac{|\nabla w|^{p-2}}{2w^q} \left[\begin{array}{@{}c@{}} \partial_t \\ \nabla \end{array}\right] |\nabla w|^2 - q\frac{|\nabla w|^p}{w^{q+1}} \left[\begin{array}{@{}c@{}} \partial_t \\ \nabla \end{array}\right] w. \end{equation}

Now an application of the divergence operator to the second line gives

(6.8)\begin{align} \Delta \frac{|\nabla w|^p}{w^q} & = \frac{p}{2} \frac{|\nabla w|^{p-2}}{w^q} \Delta |\nabla w|^2 + \frac{p}{2w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle \nonumber\\ & \quad- pq \frac{|\nabla w|^{p-2}}{w^{q+1}} \langle \nabla |\nabla w|^2, \nabla w \rangle -q \frac{|\nabla w|^p}{w^{q+1}} \Delta w + q(q+1) \frac{|\nabla w|^{p+2}}{w^{q+2}}, \end{align}

and thus after using the relation $\Delta _\phi (|\nabla w|^p/w^q) = \Delta (|\nabla w|^p/w^q) - \langle \nabla \phi,\, |\nabla w|^p/w^q \rangle$ it follows that

(6.9)\begin{align} {\mathscr L}_\phi^{\mathsf a} \left( \frac{|\nabla w|^p}{w^q} \right)& =\frac{p}{2} \frac{|\nabla w|^{p-2}}{w^q} {\mathscr L}_\phi^{\mathsf a} (|\nabla w|^2) - \frac{p}{2w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle \\ & \quad+ pq \frac{|\nabla w|^{p-2}}{w^{q+1}} \langle \nabla |\nabla w|^2, \nabla w \rangle -q\frac{|\nabla w|^p}{w^{q+1}} {\mathscr L}_\phi^{\mathsf a}(w) \nonumber\\ & \quad+ \frac{1}{2} (p+2q-2) \frac{|\nabla w|^p}{w^q} - q(q+1) \frac{|\nabla w|^{p+2}}{w^{q+2}}. \nonumber \end{align}

Next by making note of the weighted Bochner–Weitzenböck formula in lemma 3.1 and the differentiation identity in lemma 3.2 it is seen that

(6.10)\begin{equation} \left[\begin{array}{@{}c@{}} \partial_t \\ \Delta_\phi \end{array}\right] |\nabla w|^2 = 2 \left[\begin{array}{@{}c@{}} \langle \nabla w, \nabla \partial_t w \rangle - (1/2) [\partial_t g](\nabla w, \nabla w) \\ |\nabla \nabla w|^2 + \langle \nabla w, \nabla \Delta_\phi w \rangle + {\mathscr Ric}_\phi(g) \end{array}\right].\end{equation}

Therefore, $(\partial _t - \Delta _\phi ) |\nabla w|^2 = - \partial _t g + 2 \langle \nabla w,\, \nabla \partial _t w \rangle - 2[{\mathscr Ric}_\phi (g) + |\nabla \nabla w|^2 + \langle \nabla w,\, \nabla \Delta _\phi w \rangle ]$ and so together with the equation $\partial _t w = \Delta _\phi w +\mathsf a(x,\,t)w+ \mathscr G (t,\,x,\,w)$ this gives

(6.11)\begin{align} {\mathscr L}_\phi^{\mathsf a} |\nabla w|^2 & = (\partial_t - {\mathsf a} - \Delta_\phi) |\nabla w|^2 ={-}[\partial_t g + 2 {\mathscr Ric}_\phi(g)] + \mathsf a|\nabla w|^2 \nonumber\\ & \quad+ 2 w\langle \nabla w, \nabla \mathsf a \rangle + 2 \langle \nabla w, \nabla \mathscr G \rangle - 2 |\nabla \nabla w|^2. \end{align}

Therefore, upon substitution back in (6.9) it follows that

(6.12)\begin{align} {\mathscr L}_\phi^{\mathsf a} \left( \frac{|\nabla w|^p}{w^q} \right) & ={-}\frac{p}{2} \frac{|\nabla w|^{p-2}}{w^q} [ \partial_t g + 2{\mathscr Ric}_\phi ] + p \frac{|\nabla w|^{p-2}}{w^q} \langle \nabla w, \nabla \mathscr G \rangle \nonumber\\ & \quad+ \frac{|\nabla w|^{p-2}}{w^q} [(p-1) |\nabla w|^2 \mathsf a + pw\langle \nabla w, \nabla \mathsf a \rangle] \nonumber\\ & \quad- p\frac{|\nabla w|^{p-2}}{w^q} \left( |\nabla \nabla w|^2 - \frac{q}{w} \langle \nabla |\nabla w|^2, \nabla w \rangle + \frac{q}{p}(q+1) \frac{|\nabla w|^{4}}{w^{2}} \right) \nonumber\\ & \quad- \frac{p}{2w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle -q\frac{|\nabla w|^p}{w^{q+1}} [\mathsf a w +\mathscr G]. \end{align}

Now for the term inside the brackets on the third line of the right note that

(6.13)\begin{align} & |\nabla \nabla w|^2 - \frac{q}{w} \langle \nabla |\nabla w|^2, \nabla w \rangle + \frac{q}{p}(q+1) \frac{|\nabla w|^{4}}{w^{2}} \nonumber\\ & \quad= \left| \nabla \nabla w - \frac{q}{w} [\nabla w \otimes \nabla w] \right|^2 + \left[ \frac{q}{p}(q+1) - q^2 \right] \frac{|\nabla w|^4}{w^2}, \end{align}

and therefore substituting back results in the formulation

\begin{align*} {\mathscr L}_\phi^{\mathsf a} \left( \frac{|\nabla w|^p}{w^q} \right) & ={-}\frac{p}{2} \frac{|\nabla w|^{p-2}}{w^q} [\partial_t g + 2{\mathscr Ric}_\phi] + p \frac{|\nabla w|^{p-2}}{w^q} \langle \nabla w, \nabla \mathscr G \rangle \\ & \quad+ \frac{|\nabla w|^{p-2}}{w^q} [(p-1)|\nabla w|^2 \mathsf a + pw\langle \nabla w, \nabla \mathsf a\rangle]\\ & \quad- \frac{p}{2w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle -q\frac{|\nabla w|^p}{w^{q+1}} [\mathsf aw +\mathscr G] \\ & \quad- p\frac{|\nabla w|^{p-2}}{w^q} \left| \nabla \nabla w - \frac{q}{w} [\nabla w \otimes \nabla w] \right|^2 - q[q+1-pq] \frac{|\nabla w|^{p+2}}{w^{q+2}}. \end{align*}

Now returning to (6.5) and making note of the above fragments and the basic identity $\nabla \mathscr G(t,\,x,\,w) = \mathscr G_x(t,\,x,\,w) + \mathscr G_w(t,\,x,\,w) \nabla w$ it follows that

(6.14)\begin{align} {\mathscr L}_\phi^{\mathsf a} ({\bf X}^{p,q}_\zeta[w]) & = \zeta' \frac{|\nabla w|^p}{w^q} + \zeta {\mathscr L}_\phi^{\mathsf a} \left( \frac{|\nabla w|^p}{w^q} \right) + {\mathscr L}_\phi^{\mathsf a} (\Gamma(w)) \nonumber\\ & = \zeta' \frac{|\nabla w|^p}{w^q} - p \zeta \frac{|\nabla w|^{p-2}}{w^q} \left[ \frac{1}{2} \partial_t g + {\mathscr Ric}_\phi \right] -q \zeta \frac{|\nabla w|^p}{w^{q+1}} [\mathsf aw +\mathscr G] \nonumber\\ & \quad+ \zeta \frac{|\nabla w|^{p-2}}{w^q} \bigg\{ p|\nabla w|^2 \mathscr G_w + p \langle \nabla w, \mathscr G_x\rangle + p |\nabla w|^2 \mathsf a + pw\langle \nabla w, \nabla \mathsf a\rangle \bigg\} \nonumber\\ & \quad- \frac{p \zeta}{2w^q} \langle \nabla |\nabla w|^{p-2}, \nabla |\nabla w|^2 \rangle - q[q+1-pq] \zeta \frac{|\nabla w|^{p+2}}{w^{q+2}} \nonumber\\ & \quad- p \zeta \frac{|\nabla w|^{p-2}}{w^q} \left| \nabla \nabla w - \frac{q}{w} [\nabla w \otimes \nabla w] \right|^2 - \left[ \zeta \frac{|\nabla w|^p}{w^q} + \Gamma(w) \right] \mathsf a\nonumber\\ & \quad+ \Gamma'(w) [\mathsf aw+\mathscr G ] - \Gamma''(w) |\nabla w|^2 \end{align}

which is the desired conclusion. The final assertion follows by using the flow inequality $\partial _t g + 2{\mathscr Ric}_\phi (g) \ge -2 \mathsf {k} g$ and $\langle \nabla |\nabla w|^{p-2},\, \nabla |\nabla w|^2\rangle \ge 0$ when $p\ge 2$. The last inequality follows by writing $W=|\nabla w|^2$ and setting $\alpha =(p-2)/2$ and noting that the expression is $\langle \nabla W^\alpha,\, \nabla W \rangle = \alpha W^{\alpha -1} |\nabla W|^2 \ge 0$.

We now give two consequences of this evolution identity to global gradient estimates. Here $w$ is taken a positive smooth solution to ${\mathscr L}_\phi [w] = (\partial _t - \Delta _\phi ) w = {\mathscr G}(t,\,x,\,w)$ [i.e., with $\mathsf a(x,\,t) =0$] whilst the pair $(g,\,\phi )$ is assumed to evolve under a ${\mathsf k}$-super Perelman–Ricci flow. Furthermore, as we will be applying the maximum principle for the sake of convenience $M$ is taken to be closed.

Corollary 6.2 Under the assumptions of lemma 6.1, if $q[q+1-pq] \ge 0$, $\Gamma ''(w) \ge 0$, $\Gamma ' (w)\mathscr G(w) \le 0$ and $q\mathscr G(w)/(pw) - \mathscr G'(w) \ge a$ along $w$ then for $x \in M$ and $0< t \le T$

(6.15)\begin{equation} \frac{|\nabla w|^p}{w^q} (x,t) \le e^{p(\mathsf{k}-a)t} \left\{ \max_{M} \left[ \frac{|\nabla w|^p}{w^q} + \Gamma(w) \right] (x, 0) - \Gamma(w)(x, t) \right\}.\end{equation}

Proof. Utilizing (6.4), $\Gamma ''(w) \ge 0$, $\Gamma '(w)\mathscr G(w) \le 0$ and $p\mathscr G'(w) - q\mathscr G(w)/w \le -ap$ for some $a$ we can write²

(6.16)\begin{align} {\mathscr L}_\phi({\bf X}^{p,q}_\zeta[w]) & \le~\frac{|\nabla w|^p}{w^q} \left[ \zeta' + p \zeta \mathsf{k} + p \zeta \mathscr G'(w) - q \zeta \frac{\mathscr G(w)}{w} \right] \nonumber\\ & \quad- q[q+1 - pq] \zeta \frac{|\nabla w|^{p+2}}{w^{q+2}} + \Gamma'(w) \mathscr G(w) - \Gamma''(w) |\nabla w|^2 \nonumber\\ & \le~\frac{|\nabla w|^p}{w^q} [\zeta' + p (\mathsf{k}-a)] \zeta - q[q+1-pq] \zeta \frac{|\nabla w|^{p+2}}{w^{q+2}}. \end{align}

The function $\zeta (t) = X e^{-p(\mathsf {k}-a)t}$ is non-negative, smooth and satisfies $\zeta '+ p(\mathsf {k}-a)\zeta =0$ (for $t \ge 0$ and fixed $X>0$). Thus by substituting in (6.16) and noting $q(q+1-pq) \ge 0$ we have ${\mathscr L}_\phi ({\bf X}^{p,q}_\zeta [w]) \le 0$. The assertion is now a consequence of the weak maximum principle giving

(6.17)\begin{equation} {\bf X}^{p,q}_\zeta[w](x,t) \le \max_M {\bf X}^{p,q}_\zeta[w] |_{t=0}.\end{equation}

The proof is thus complete.

Corollary 6.3 Under the assumptions of lemma 6.1 if $\mathscr G,\, \mathscr G' \le 0$ along $w$ and (4.1) holds with $\mathsf {k} \ge 0$ then for $x \in M$ and $0< t \le T$

(6.18)\begin{equation} |\nabla w|^2(x,t) \le \frac{1+2\mathsf{k}t}{2t} \left[ \max_M w^2(x,0) - w^2(x,t) \right].\end{equation}

Proof. Setting $p=2$, $q=0$ and $\Gamma (w)= w^2/2$ in (6.2) gives ${\bf X}={\bf X}^{2,0}_\zeta [w] = \zeta |\nabla w|^2 + w^2/2$ and so from (6.4) it follows that

(6.19)\begin{align} {\mathscr L}_\phi ({\bf X}[w]) & = {\mathscr L}_\phi (\zeta |\nabla w|^2 + w^2/2) \nonumber\\ & \le [\zeta' + 2\mathsf{k} \zeta + 2 \zeta \mathscr G'(w)] |\nabla w|^2 + w \mathscr G (w) - |\nabla w|^2 \nonumber\\ & \le (\zeta' + 2\mathsf{k} \zeta -1) |\nabla w|^2 + 2 \zeta \mathscr G' (w) |\nabla w|^2 + w \mathscr G (w). \end{align}

Now when $\mathsf {k} \ge 0$ by taking $\zeta (t) = t/(1+2\mathsf {k} t)$ we have $(\zeta ' + 2 \mathsf {k} \zeta -1) \le 0$ and so subject to $\mathscr G,\, \mathscr G' \le 0$ we have ${\mathscr L}_\phi ({\bf X}[w]) \le 0$. The conclusion now follows by an application of the weak maximum principle.