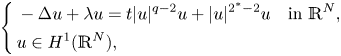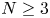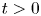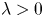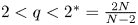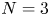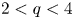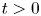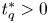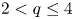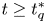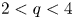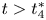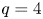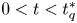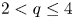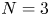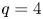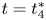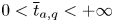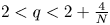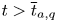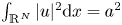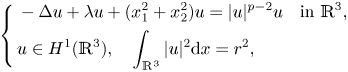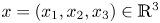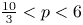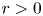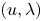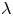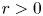1. Introduction
In the celebrated paper [Reference Gidas, Ni and Nirenberg17], the well-known Gidas–Ni–Nirenberg theorem asserts that the positive solution of the following equation,

must be radially symmetric up to translations under some suitable conditions on the nonlinearities $f(u)$![]() , where $N\geq 1$
, where $N\geq 1$![]() . Since then, an interesting and important problem is the uniqueness of the positive solution to (1.1). Kwong proved such uniqueness result in [Reference Kwong22] for the power-type nonlinearities $f(u)=u^{p-1}-u$
. Since then, an interesting and important problem is the uniqueness of the positive solution to (1.1). Kwong proved such uniqueness result in [Reference Kwong22] for the power-type nonlinearities $f(u)=u^{p-1}-u$![]() with $2< p<2^{*}$
with $2< p<2^{*}$![]() , where $2^{*}$
, where $2^{*}$![]() is the critical Sobolev exponent given by $2^{*}=+\infty$
is the critical Sobolev exponent given by $2^{*}=+\infty$![]() for $N=1,2$
for $N=1,2$![]() and $2^{*}=2N/(N-2)$
and $2^{*}=2N/(N-2)$![]() for $N\geq 3$
for $N\geq 3$![]() (see the earlier papers [Reference Coffman12] for the cubic nonlinearity $f(u)=u^{3}-u$
(see the earlier papers [Reference Coffman12] for the cubic nonlinearity $f(u)=u^{3}-u$![]() and [Reference McLeod and Serrin27–Reference Peletier and Serrin29] for general nonlinearities). The extension of Kwong's result can be found in [Reference McLeod26, Reference Pucci and Serrin30, Reference Serrin and Tang31] and so far, to our best knowledge, the most general extension of Kwong's result is due to Serrin and Tang in [Reference Serrin and Tang31]: The positive solution of (1.1) is unique if there exists $b>0$
and [Reference McLeod and Serrin27–Reference Peletier and Serrin29] for general nonlinearities). The extension of Kwong's result can be found in [Reference McLeod26, Reference Pucci and Serrin30, Reference Serrin and Tang31] and so far, to our best knowledge, the most general extension of Kwong's result is due to Serrin and Tang in [Reference Serrin and Tang31]: The positive solution of (1.1) is unique if there exists $b>0$![]() such that $\frac {f(u)-u}{u-b}>0$
such that $\frac {f(u)-u}{u-b}>0$![]() for $u\not =b$
for $u\not =b$![]() and the quotient $\frac {f'(u)u-u}{f(u)-u}$
and the quotient $\frac {f'(u)u-u}{f(u)-u}$![]() is nonincreasing of $u\in (b, +\infty )$
is nonincreasing of $u\in (b, +\infty )$![]() , which is not the case of the mixed nonlinearities $f(u)=\mu u^{q-1}+\nu u^{p-1}-\lambda u$
, which is not the case of the mixed nonlinearities $f(u)=\mu u^{q-1}+\nu u^{p-1}-\lambda u$![]() with $2< q\not =p<2^{*}$
with $2< q\not =p<2^{*}$![]() and $\mu,\nu,\lambda >0$
and $\mu,\nu,\lambda >0$![]() . In this case, (1.1) reads as
. In this case, (1.1) reads as

By rescaling, (1.2) is equivalent to

In an interesting paper [Reference Dávila, del Pino and Guerra14], Davila et al. proved that for $N=3$![]() , $2< q<4$
, $2< q<4$![]() , $p<6$
, $p<6$![]() with sufficiently close to $6$
with sufficiently close to $6$![]() and $t>0$
and $t>0$![]() sufficiently large, (1.3) has three positive radial solutions, which yields a rather striking result that Kwong's uniqueness result is in general not true for the mixed nonlinearities. Thus, the uniqueness of the positive radial solution of (1.3) (or more general, (1.1)) remains largely open. It is worth pointing out that the mentioned papers are all devoted to the Sobolev subcritical case for $N\geq 3$
sufficiently large, (1.3) has three positive radial solutions, which yields a rather striking result that Kwong's uniqueness result is in general not true for the mixed nonlinearities. Thus, the uniqueness of the positive radial solution of (1.3) (or more general, (1.1)) remains largely open. It is worth pointing out that the mentioned papers are all devoted to the Sobolev subcritical case for $N\geq 3$![]() , that is, $\lim _{u\to +\infty }\frac {f(u)}{u^{2^{*}}}=0$
, that is, $\lim _{u\to +\infty }\frac {f(u)}{u^{2^{*}}}=0$![]() .
.
In the Sobolev critical case for $N\geq 3$![]() , that is, $\lim _{u\to +\infty }\frac {f(u)}{u^{2^{*}-1}}>0$
, that is, $\lim _{u\to +\infty }\frac {f(u)}{u^{2^{*}-1}}>0$![]() , the well-known Gidas–Ni–Nirenberg theorem still holds, that is, positive solutions must be radially symmetric up to translations. However, for $N\geq 3$
, the well-known Gidas–Ni–Nirenberg theorem still holds, that is, positive solutions must be radially symmetric up to translations. However, for $N\geq 3$![]() , compared to the Sobolev subcritical case (cf. [Reference Berestycki and Lions8]), the existence of positive solutions of (1.1) is more complicated in the Sobolev critical case. For example, for (1.3), the special case of (1.1), the existence of positive solutions is established in [Reference Akahori, Ibrahim, Kikuchi and Nawa2, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4, Reference Alves, Souto and Montenegro6, Reference Liu, Liao and Tang24, Reference Zhang and Zou35], which can be summarized as follows:
, compared to the Sobolev subcritical case (cf. [Reference Berestycki and Lions8]), the existence of positive solutions of (1.1) is more complicated in the Sobolev critical case. For example, for (1.3), the special case of (1.1), the existence of positive solutions is established in [Reference Akahori, Ibrahim, Kikuchi and Nawa2, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4, Reference Alves, Souto and Montenegro6, Reference Liu, Liao and Tang24, Reference Zhang and Zou35], which can be summarized as follows:
Theorem 1.1 Let $N\geq 3$![]() and $p=2^{*}$
and $p=2^{*}$![]() . Then (1.3) has a positive radial solution which is also a ground-state, provided that
. Then (1.3) has a positive radial solution which is also a ground-state, provided that
(a) $N\geq 4,$
 $2< q<2^{*}$
$2< q<2^{*}$ and $t>0;$
and $t>0;$
(b) $N=3,$
 $4< q<6$
$4< q<6$ and $t>0;$
and $t>0;$
(c) $N=3,$
 $2< q\leq 4$
$2< q\leq 4$ and $t>0$
and $t>0$ sufficiently large.
sufficiently large.
Theorem 1.1 is proved by adapting the classical ideas of Brezís and Nirenberg in [Reference Brézis and Nirenberg9], that is, using the Aubin–Talanti bubbles (cf. (2.1)) as test functions to control the energy values so that the $(PS)$![]() sequences of the associated functional, corresponding to (1.3) with $p=2^{*}$
sequences of the associated functional, corresponding to (1.3) with $p=2^{*}$![]() , are compact at the ground-state level. This strategy is invalid for $N=3$
, are compact at the ground-state level. This strategy is invalid for $N=3$![]() , $2< q\leq 4$
, $2< q\leq 4$![]() and $t>0$
and $t>0$![]() not sufficiently large. Thus, whether (1.3) with $p=2^{*}$
not sufficiently large. Thus, whether (1.3) with $p=2^{*}$![]() always has a positive radial solution is not clear. Note that according to the concentration-compactness principle (cf. [Reference Lions23]), the only possible way that the $(PS)$
always has a positive radial solution is not clear. Note that according to the concentration-compactness principle (cf. [Reference Lions23]), the only possible way that the $(PS)$![]() sequences of the associated functional loss the compactness at the ground-state level is that they concentrate at single points and behaviour like a Aubin–Talanti bubble under some suitable scalings in passing to the limit. Thus, by the energy estimates in [Reference Akahori, Ibrahim, Kikuchi and Nawa2, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4, Reference Alves, Souto and Montenegro6, Reference Liu, Liao and Tang24, Reference Zhang and Zou35], it is reasonable to think that (1.3) with $p=2^{*}$
sequences of the associated functional loss the compactness at the ground-state level is that they concentrate at single points and behaviour like a Aubin–Talanti bubble under some suitable scalings in passing to the limit. Thus, by the energy estimates in [Reference Akahori, Ibrahim, Kikuchi and Nawa2, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4, Reference Alves, Souto and Montenegro6, Reference Liu, Liao and Tang24, Reference Zhang and Zou35], it is reasonable to think that (1.3) with $p=2^{*}$![]() has no ground-states for $N=3$
has no ground-states for $N=3$![]() , $2< q\leq 4$
, $2< q\leq 4$![]() and $t>0$
and $t>0$![]() not sufficiently large. On the other hand, the uniqueness of positive radial solutions to (1.3) with $p=2^{*}$
not sufficiently large. On the other hand, the uniqueness of positive radial solutions to (1.3) with $p=2^{*}$![]() seems also very complicated. If $3\leq N\leq 6$
seems also very complicated. If $3\leq N\leq 6$![]() and $(N+2)/(N-2)< q<2^{*}$
and $(N+2)/(N-2)< q<2^{*}$![]() then Pucci and Serrin in [Reference Pucci and Serrin30] proved that (1.3) with $p=2^{*}$
then Pucci and Serrin in [Reference Pucci and Serrin30] proved that (1.3) with $p=2^{*}$![]() has at most one positive radial solution. Recently, Akahori et al. in [Reference Akahori, Ibrahim and Kikuchi1, Reference Akahori, Ibrahim, Kikuchi and Nawa3, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4] and Coles and Gustafson in [Reference Coles and Gustafson13] proved that the radial ground-state of (1.3) with $p=2^{*}$
has at most one positive radial solution. Recently, Akahori et al. in [Reference Akahori, Ibrahim and Kikuchi1, Reference Akahori, Ibrahim, Kikuchi and Nawa3, Reference Akahori, Ibrahim, Ikoma, Kikuchi and Nawa4] and Coles and Gustafson in [Reference Coles and Gustafson13] proved that the radial ground-state of (1.3) with $p=2^{*}$![]() is unique and nondegenerate for all small $t>0$
is unique and nondegenerate for all small $t>0$![]() when $N\geq 5$
when $N\geq 5$![]() and $q\in (2, 2^{*})$
and $q\in (2, 2^{*})$![]() or $N=3$
or $N=3$![]() and $q\in (4, 2^{*})$
and $q\in (4, 2^{*})$![]() ; and for all large $t>0$
; and for all large $t>0$![]() when $N\geq 3$
when $N\geq 3$![]() and $2+4/N< q<2^{*}$
and $2+4/N< q<2^{*}$![]() . However, the uniqueness of positive radial solutions seems not true for (1.3) with $p=2^{*}$
. However, the uniqueness of positive radial solutions seems not true for (1.3) with $p=2^{*}$![]() in general, since it is suggested in [Reference Dávila, del Pino and Guerra14] by the numerical evidence that (1.3) with $p=2^{*}$
in general, since it is suggested in [Reference Dávila, del Pino and Guerra14] by the numerical evidence that (1.3) with $p=2^{*}$![]() has two positive radial solutions for $N=3$
has two positive radial solutions for $N=3$![]() , $2< q<4$
, $2< q<4$![]() and $t>0$
and $t>0$![]() sufficiently large. Moreover, Chen et al. in [Reference Chen, Dávila and Guerra10] proved the existence of arbitrary large number of bubble-tower positive solutions of (1.3) in the slightly supercritical case when $q<2^{*}< p=2^{*}+\varepsilon$
sufficiently large. Moreover, Chen et al. in [Reference Chen, Dávila and Guerra10] proved the existence of arbitrary large number of bubble-tower positive solutions of (1.3) in the slightly supercritical case when $q<2^{*}< p=2^{*}+\varepsilon$![]() with $\varepsilon >0$
with $\varepsilon >0$![]() sufficiently small. We also mention the paper [Reference Ferrero and Gazzola16], in which the authors proved the existence of positive radial solutions to (1.3) for $2< q<2^{*}\leq p$
sufficiently small. We also mention the paper [Reference Ferrero and Gazzola16], in which the authors proved the existence of positive radial solutions to (1.3) for $2< q<2^{*}\leq p$![]() with $t>0$
with $t>0$![]() sufficiently large and (1.3) has no positive solutions for $2< q<2^{*}< p$
sufficiently large and (1.3) has no positive solutions for $2< q<2^{*}< p$![]() with $t>0$
with $t>0$![]() sufficiently small via ODE's methods.
sufficiently small via ODE's methods.
Inspired by the above facts, we shall explore the existence and nonexistence of positive solutions of (1.3) with $p=2^{*}$![]() by studying the existence and nonexistence of ground-states of (1.3) for $N=3$
by studying the existence and nonexistence of ground-states of (1.3) for $N=3$![]() and $2< q\leq 4$
and $2< q\leq 4$![]() . We shall also explore the uniqueness of positive solutions of (1.3) with $p=2^{*}$
. We shall also explore the uniqueness of positive solutions of (1.3) with $p=2^{*}$![]() by giving a rigorous proof of the numerical conjecture in [Reference Dávila, del Pino and Guerra14].
by giving a rigorous proof of the numerical conjecture in [Reference Dávila, del Pino and Guerra14].
Let us first introduce some necessary notations. By classical elliptic estimates, for $N\geq 3$![]() and $p=2^{*}$
and $p=2^{*}$![]() , (1.3) is equivalent to
, (1.3) is equivalent to

where $t>0$![]() , $\lambda >0$
, $\lambda >0$![]() and $2< q<2^{*}$
and $2< q<2^{*}$![]() . Clearly, by rescaling if necessary, it is sufficiently to consider the case $\lambda =1$
. Clearly, by rescaling if necessary, it is sufficiently to consider the case $\lambda =1$![]() for (1.4). Let
for (1.4). Let
where
is the corresponding functional of (1.4) with $\lambda =1$![]() and
and
is the usual Nehari manifold. Here, $\|\cdot \|_p$![]() is the usual norm in the Lebesgue space $L^{p}(\mathbb {R}^{N})$
is the usual norm in the Lebesgue space $L^{p}(\mathbb {R}^{N})$![]() .
.
Definition 1.1 We say that $u$![]() is a ground-state of (1.4) if $u$
is a ground-state of (1.4) if $u$![]() is a nontrivial solution of (1.4) with $\mathcal {E}_t(u)=m(t)$
is a nontrivial solution of (1.4) with $\mathcal {E}_t(u)=m(t)$![]() .
.
Now, our main result is the following.
Theorem 1.2 Let $\lambda =1,$![]() $N=3$
$N=3$![]() and $2< q\leq 4$
and $2< q\leq 4$![]() . Then there exists $t_q^{*}>0,$
. Then there exists $t_q^{*}>0,$![]() which may depend on $q,$
which may depend on $q,$![]() such that
such that
(1) (1.4) has ground-states for $t\geq t_q^{*}$
 and has no ground-states for $0< t< t_q^{*}$
and has no ground-states for $0< t< t_q^{*}$ in the case of $2< q<4$
in the case of $2< q<4$ .
.(2) (1.4) has ground-states for $t> t_4^{*}$
 and has no ground-states for $0< t< t_4^{*}$
and has no ground-states for $0< t< t_4^{*}$ in the case of $q=4$
in the case of $q=4$ .
.
Moreover, if $2< q<4$![]() then there exists $t_q>0$
then there exists $t_q>0$![]() , which may depend on $q$
, which may depend on $q$![]() , such that (1.4) has two positive radial solutions $u_{t,1}$
, such that (1.4) has two positive radial solutions $u_{t,1}$![]() and $u_{t,2}$
and $u_{t,2}$![]() for $t>t_q$
for $t>t_q$![]() , where $u_{t,1}$
, where $u_{t,1}$![]() is a ground-state with $\|u_{t,1}\|_\infty \sim t^{-\frac {1}{q-2}}$
is a ground-state with $\|u_{t,1}\|_\infty \sim t^{-\frac {1}{q-2}}$![]() and $u_{t,2}$
and $u_{t,2}$![]() is a blow-up solution with
is a blow-up solution with

as $t\to +\infty$![]() .
.
Remark 1.1 Theorem 1.2, together with theorem 1.1, almost completely solves the existence of ground-states to (1.4), except for $N=3$![]() , $q=4$
, $q=4$![]() and $t=t_4^{*}$
and $t=t_4^{*}$![]() . Moreover, theorem 1.2 also verifies the numerical conjecture in [Reference Dávila, del Pino and Guerra14].
. Moreover, theorem 1.2 also verifies the numerical conjecture in [Reference Dávila, del Pino and Guerra14].
The proof of theorem 1.2 is based on our very recent study on the normalized solution of (1.4) with the additional condition $\|u\|_2^{2}=a^{2}$![]() , where $a>0$
, where $a>0$![]() . We remark that we shall call $u$
. We remark that we shall call $u$![]() is a fixed-frequency solution of (1.4) if the frequency $\lambda$
is a fixed-frequency solution of (1.4) if the frequency $\lambda$![]() is fixed, since for the normalized solution of (1.4), the frequency $\lambda$
is fixed, since for the normalized solution of (1.4), the frequency $\lambda$![]() is a part of unknowns, which appears as a Lagrange multiplier. Now, let us explain our ideas in proving theorem 1.2. Let $\mu >0$
is a part of unknowns, which appears as a Lagrange multiplier. Now, let us explain our ideas in proving theorem 1.2. Let $\mu >0$![]() , $a>0$
, $a>0$![]() and $(u_\mu, \lambda _\mu )$
and $(u_\mu, \lambda _\mu )$![]() be a normalized solution of (1.4) for $t=\mu$
be a normalized solution of (1.4) for $t=\mu$![]() with the additional condition $\|u_\mu \|_2^{2}=a^{2}$
with the additional condition $\|u_\mu \|_2^{2}=a^{2}$![]() , that is, $(u_\mu, \lambda _\mu )$
, that is, $(u_\mu, \lambda _\mu )$![]() is a solution of the following system:
is a solution of the following system:

then by the Pohozaev identity satisfied by $u_\mu$![]() (cf. [Reference Wei and Wu33, (4.7)]),
(cf. [Reference Wei and Wu33, (4.7)]),
where $\gamma _q=\frac {N(q-2)}{2q}$![]() . Let
. Let
then by direct calculations, we know that $v_\mu$![]() is a fixed-frequency solution of (1.4) for $\lambda =1$
is a fixed-frequency solution of (1.4) for $\lambda =1$![]() and $t=\mu \lambda _\mu ^{\frac {q\gamma _q-q}{2}}$
and $t=\mu \lambda _\mu ^{\frac {q\gamma _q-q}{2}}$![]() . By (1.8), we also have
. By (1.8), we also have
Thus, by letting
we know that $(v_\mu,t_\mu )$![]() solves the following system:
solves the following system:

Clearly, if $(v, t)$![]() is a solution of the system (1.11), then by letting
is a solution of the system (1.11), then by letting

$(u_\mu, \lambda _\mu )$![]() is also a normalized solution of (1.4) for $t=\mu$
is also a normalized solution of (1.4) for $t=\mu$![]() with the additional condition $\|u_\mu \|_2^{2}=a^{2}$
with the additional condition $\|u_\mu \|_2^{2}=a^{2}$![]() , that is $(u_\mu, \lambda _\mu )$
, that is $(u_\mu, \lambda _\mu )$![]() is also a normalized solution of (1.7). Thus, by our above observations, normalized solutions of (1.4) is equivalent to fixed-frequency solutions of (1.4) with another additional condition. Since we made a detail study on some special normalized solutions of (1.4) in [Reference Wei and Wu33], we could use these detailed estimates to derive theorem 1.2.
is also a normalized solution of (1.7). Thus, by our above observations, normalized solutions of (1.4) is equivalent to fixed-frequency solutions of (1.4) with another additional condition. Since we made a detail study on some special normalized solutions of (1.4) in [Reference Wei and Wu33], we could use these detailed estimates to derive theorem 1.2.
Our observations on the relations between fixed-frequency solutions and normalized solutions of (1.4) also bring in some new lights to study the normalized solutions of (1.4). Indeed, let $v_t$![]() be a fixed-frequency solution of (1.4), then by the above observations, finding normalized solutions of (1.4) is equivalent to finding solutions of the following equation:
be a fixed-frequency solution of (1.4), then by the above observations, finding normalized solutions of (1.4) is equivalent to finding solutions of the following equation:
This is a reduction, which heavily depends on the scaling technique and the Pohozaev identity, since we reduce the solvability of (1.4) in $H^{1}(\mathbb {R}^{N})$![]() to the solvability of (1.13) in $\mathbb {R}^{+}$
to the solvability of (1.13) in $\mathbb {R}^{+}$![]() . Let
. Let
Then, $\mathcal {A}_\mu |_{S_a}(u)$![]() is the corresponding functional of (1.7), where $S_a=\{u\in H^{1}(\mathbb {R}^{N})\mid \|u\|_2^{2}=a^{2}\}$
is the corresponding functional of (1.7), where $S_a=\{u\in H^{1}(\mathbb {R}^{N})\mid \|u\|_2^{2}=a^{2}\}$![]() .
.
Definition 1.2 We say that $u$![]() is a normalized ground-state of (1.7) if $u$
is a normalized ground-state of (1.7) if $u$![]() is a solution of (1.7) and $\mathcal {A}_\mu (u)\leq \mathcal {A}_\mu (v)$
is a solution of (1.7) and $\mathcal {A}_\mu (u)\leq \mathcal {A}_\mu (v)$![]() for any other solutions of (1.7).
for any other solutions of (1.7).
By (1.12), if $(u_\mu, \lambda _\mu )$![]() is a solution of (1.7), then,
is a solution of (1.7), then,
where $(v_\mu, t_\mu )$![]() is a solution of (1.11). Thus, normalized ground-states of (1.7) must be generated by positive fixed-frequency ground-states of (1.4) through the equation (1.13), that is, $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$
is a solution of (1.11). Thus, normalized ground-states of (1.7) must be generated by positive fixed-frequency ground-states of (1.4) through the equation (1.13), that is, $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$![]() where
where
and
with $\lambda _\mu =(\frac {t}{\mu })^{\frac {2}{q\gamma _q-q}}$![]() and
and
Indeed, let $(u_{*,\mu },\lambda _{*,\mu })$![]() be any solution of (1.8) with $\lambda _{*,\mu }>0$
be any solution of (1.8) with $\lambda _{*,\mu }>0$![]() . If $v_{*,\mu }$
. If $v_{*,\mu }$![]() is not a fixed-frequency ground-state of (1.4) with $t=t_{*,\mu }$
is not a fixed-frequency ground-state of (1.4) with $t=t_{*,\mu }$![]() where $v_{*,\mu }$
where $v_{*,\mu }$![]() and $t_{*,\mu }$
and $t_{*,\mu }$![]() are given by (1.9) and (1.10), respectively, then there exists $\overline {v}\in H^{1}(\mathbb {R}^{N})$
are given by (1.9) and (1.10), respectively, then there exists $\overline {v}\in H^{1}(\mathbb {R}^{N})$![]() such that $\overline {v}$
such that $\overline {v}$![]() is a fixed-frequency ground-state of (1.11) and
is a fixed-frequency ground-state of (1.11) and
It follows that
which implies that $\mathcal {A}_\mu (v_{*,\mu })>\mathcal {A}_\mu (\overline {v}_\mu )$![]() where $\overline {u}_\mu$
where $\overline {u}_\mu$![]() is given by (1.12). Therefore, if (1.7) has a solution then $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$
is given by (1.12). Therefore, if (1.7) has a solution then $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$![]() . In other words, either (1.7) has no solutions or $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$
. In other words, either (1.7) has no solutions or $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$![]() . Note that by theorems 1.1 and 1.2, $\mathbb {D}_{fre}\not =\emptyset$
. Note that by theorems 1.1 and 1.2, $\mathbb {D}_{fre}\not =\emptyset$![]() . Thus, $\mathbb {P}_{nor}\not =\emptyset$
. Thus, $\mathbb {P}_{nor}\not =\emptyset$![]() which implies that $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$
which implies that $\mathbb {D}_{nor}\subset \mathbb {P}_{nor}$![]() . It is worth pointing out that this fact has also been pointed out in [Reference Dovetta, Serra and Tilli15, Reference Jeanjean and Lu20]. With these in minds, we can obtain the following results.
. It is worth pointing out that this fact has also been pointed out in [Reference Dovetta, Serra and Tilli15, Reference Jeanjean and Lu20]. With these in minds, we can obtain the following results.
Theorem 1.3 Let $N\geq 3$![]() and $2< q<2+\frac {4}{N}$
and $2< q<2+\frac {4}{N}$![]() . Then there exist $0<\widehat {t}_{q,a}\leq \overline {t}_{q,a}<+\infty$
. Then there exist $0<\widehat {t}_{q,a}\leq \overline {t}_{q,a}<+\infty$![]() , which may depend on $q$
, which may depend on $q$![]() and $a,$
and $a,$![]() such that (1.4) has normalized ground-states with the additional condition $\|u\|_2^{2}=a^{2}$
such that (1.4) has normalized ground-states with the additional condition $\|u\|_2^{2}=a^{2}$![]() for $0< t<\widehat {t}_{q,a}$
for $0< t<\widehat {t}_{q,a}$![]() and (1.4) has no normalized ground-states with the additional condition $\|u\|_2^{2}=a^{2}$
and (1.4) has no normalized ground-states with the additional condition $\|u\|_2^{2}=a^{2}$![]() for $t>\overline {t}_{q,a}$
for $t>\overline {t}_{q,a}$![]() .
.
Remark 1.2 Theorem 1.3, together with our recent study in [Reference Wei and Wu33], gives a completed answer to the open question proposed by Soave in [Reference Soave32].
As an application of our new reduction in finding normalized solutions of (1.4), we shall also consider the following Schrödinger equation:

where $x=(x_1,x_2,x_3)\in \mathbb {R}^{3}$![]() , $V(x)=x_1^{2}+x_2^{2}$
, $V(x)=x_1^{2}+x_2^{2}$![]() , $\frac {10}{3}< p<6$
, $\frac {10}{3}< p<6$![]() and $r>0$
and $r>0$![]() is a constant. (1.15) is studied recently by Bellazzini et al. in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7], in which the authors proved that (1.15) has a ground-state normalized solution, which is also a local minimizer of the associated functional on the $L^{2}$
is a constant. (1.15) is studied recently by Bellazzini et al. in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7], in which the authors proved that (1.15) has a ground-state normalized solution, which is also a local minimizer of the associated functional on the $L^{2}$![]() -sphere $\|u\|_2^{2}=r^{2}$
-sphere $\|u\|_2^{2}=r^{2}$![]() , with a negative Lagrange multiplier $\lambda$
, with a negative Lagrange multiplier $\lambda$![]() for $r>0$
for $r>0$![]() sufficiently small. According to the geometry of the associated functional on the $L^{2}$
sufficiently small. According to the geometry of the associated functional on the $L^{2}$![]() -sphere $\|u\|_2^{2}=r^{2}$
-sphere $\|u\|_2^{2}=r^{2}$![]() , Bellazzini et al. also conjectured in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7] that (1.15) has a second normalized solution, which is also a mountain-pass solution, for $r>0$
, Bellazzini et al. also conjectured in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7] that (1.15) has a second normalized solution, which is also a mountain-pass solution, for $r>0$![]() sufficiently small. In this paper, we prove this conjecture by obtaining the following result.
sufficiently small. In this paper, we prove this conjecture by obtaining the following result.
Theorem 1.4 Let $\frac {10}{3}< p<6$![]() . Then for $r>0$
. Then for $r>0$![]() sufficiently small, (1.15) has a second positive normalized solution $u_{r,2}$
sufficiently small, (1.15) has a second positive normalized solution $u_{r,2}$![]() , which is also a mountain-pass solution, with a positive Lagrange multiplier
, which is also a mountain-pass solution, with a positive Lagrange multiplier

where $w_\infty$![]() is the unique (up to translations) positive solution of the following equation:
is the unique (up to translations) positive solution of the following equation:

Moreover,
To prove theorem 1.4, we introduce
where $w_t$![]() is a positive ground-state of the following equation:
is a positive ground-state of the following equation:

Then by applying our new reduction argument to (1.15), we reduce finding normalized solutions of (1.15) to finding solutions of the equation $f(r,t)=0$![]() for fixed small $r>0$
for fixed small $r>0$![]() . By the uniqueness and nondegeneracy of $w_\infty$
. By the uniqueness and nondegeneracy of $w_\infty$![]() , we prove that the curve $w_t$
, we prove that the curve $w_t$![]() is continuous for $t>0$
is continuous for $t>0$![]() sufficiently large in a suitable space. Thus, (1.19) can be solved easily by the continuation method. We believe this method will be helpful in studying normalized solutions of other elliptic equations.
sufficiently large in a suitable space. Thus, (1.19) can be solved easily by the continuation method. We believe this method will be helpful in studying normalized solutions of other elliptic equations.
Notations. Throughout this paper, $C$![]() and $C'$
and $C'$![]() are indiscriminately used to denote various absolutely positive constants. $a\sim b$
are indiscriminately used to denote various absolutely positive constants. $a\sim b$![]() means that $C'b\leq a\leq Cb$
means that $C'b\leq a\leq Cb$![]() and $a\lesssim b$
and $a\lesssim b$![]() means that $a\leq Cb$
means that $a\leq Cb$![]() .
.
2. Blow-up solutions for $N=3$ and $2< q<4$
and $2< q<4$
It is well known that the Aubin–Talanti babbles,

is the only solutions to the following equation:

By [Reference Wei and Wu33, theorem 1.2], for $\mu >0$![]() sufficiently small, (1.7) has a positive radial solution $\widetilde {u}_\mu$
sufficiently small, (1.7) has a positive radial solution $\widetilde {u}_\mu$![]() with the Lagrange multiplier $\widetilde {\lambda }_\mu >0$
with the Lagrange multiplier $\widetilde {\lambda }_\mu >0$![]() such that $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$
such that $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$![]() strongly in $D^{1,2}(\mathbb {R}^{3})$
strongly in $D^{1,2}(\mathbb {R}^{3})$![]() for some $\varepsilon _0>0$
for some $\varepsilon _0>0$![]() as $\mu \to 0$
as $\mu \to 0$![]() up to a subsequence, where $U_{\varepsilon _0}$
up to a subsequence, where $U_{\varepsilon _0}$![]() is given by (2.1) and $\varepsilon _{\mu }$
is given by (2.1) and $\varepsilon _{\mu }$![]() satisfies
satisfies

Moreover, by [Reference Wei and Wu33, lemma 4.1], we have

On the other hand, in the proof of [Reference Wei and Wu33, proposition 4.2], we also show that
Proposition 2.1 Let $\lambda =1,$![]() $N=3$
$N=3$![]() and $2< q<4$
and $2< q<4$![]() . Then there exists $t_q>0$
. Then there exists $t_q>0$![]() , which may depend on $q,$
, which may depend on $q,$![]() such that (1.4) has two positive radial solutions $u_{t,1}$
such that (1.4) has two positive radial solutions $u_{t,1}$![]() and $u_{t,2}$
and $u_{t,2}$![]() for $t>t_q,$
for $t>t_q,$![]() where $u_{t,1}$
where $u_{t,1}$![]() is a ground-state with $\|u_{t,1}\|_\infty \sim t^{-\frac {1}{q-2}}$
is a ground-state with $\|u_{t,1}\|_\infty \sim t^{-\frac {1}{q-2}}$![]() and $u_{t,2}$
and $u_{t,2}$![]() is a blow-up solution with
is a blow-up solution with

as $t\to +\infty$![]() .
.
Proof. By (1.9) and (1.10), $(\widetilde {v}_\mu, \widetilde {t}_\mu )$![]() is a solution of (1.11). In particular, $\widetilde {v}_\mu$
is a solution of (1.11). In particular, $\widetilde {v}_\mu$![]() is a solution of (1.4) for $\lambda =1$
is a solution of (1.4) for $\lambda =1$![]() and $t=\widetilde {t}_\mu =\mu \widetilde {\lambda }_\mu ^{\frac {q\gamma _q-q}{2}}$
and $t=\widetilde {t}_\mu =\mu \widetilde {\lambda }_\mu ^{\frac {q\gamma _q-q}{2}}$![]() . By the well-known Gidas–Ni–Nirenberg theorem [Reference Gidas, Ni and Nirenberg17], $\widetilde {v}_{\mu }$
. By the well-known Gidas–Ni–Nirenberg theorem [Reference Gidas, Ni and Nirenberg17], $\widetilde {v}_{\mu }$![]() is radial and decreasing for $r=|x|$
is radial and decreasing for $r=|x|$![]() up to translations. Thus, without loss of generality, we may assume that $\widetilde {v}_{\mu }(0)=\max _{x\in \mathbb {R}^{N}}\widetilde {v}_{\mu }$
up to translations. Thus, without loss of generality, we may assume that $\widetilde {v}_{\mu }(0)=\max _{x\in \mathbb {R}^{N}}\widetilde {v}_{\mu }$![]() . Recall that $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$
. Recall that $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$![]() strongly in $D^{1,2}(\mathbb {R}^{3})$
strongly in $D^{1,2}(\mathbb {R}^{3})$![]() for some $\varepsilon _0>0$
for some $\varepsilon _0>0$![]() as $\mu \to 0$
as $\mu \to 0$![]() up to a subsequence, by the classical elliptic regularity and the Sobolev embedding theorem, $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$
up to a subsequence, by the classical elliptic regularity and the Sobolev embedding theorem, $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (\varepsilon _{\mu } x)\to U_{\varepsilon _0}$![]() strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$
strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$![]() for some $\alpha \in (0, 1)$
for some $\alpha \in (0, 1)$![]() as $\mu \to 0$
as $\mu \to 0$![]() up to a subsequence. In particular, $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (0)\to U_{\varepsilon _0}(0)$
up to a subsequence. In particular, $\varepsilon _{\mu }^{\frac {1}{2}}\widetilde {u}_\mu (0)\to U_{\varepsilon _0}(0)$![]() as $\mu \to 0$
as $\mu \to 0$![]() up to a subsequence. Thus, by (2.1),
up to a subsequence. Thus, by (2.1),
In the following, let us estimate $\widetilde {v}_{\mu }(0)$![]() and $\widetilde {t}_\mu$
and $\widetilde {t}_\mu$![]() as $\mu \to 0$
as $\mu \to 0$![]() . We begin with the estimate of $\widetilde {t}_\mu$
. We begin with the estimate of $\widetilde {t}_\mu$![]() . We first consider the case $2< q<3$
. We first consider the case $2< q<3$![]() . In this case, by (2.2), (2.3) and (2.4), $\widetilde {\lambda }_\mu \sim \varepsilon _\mu ^{2},$
. In this case, by (2.2), (2.3) and (2.4), $\widetilde {\lambda }_\mu \sim \varepsilon _\mu ^{2},$![]() which, together with (1.10), implies
which, together with (1.10), implies
For $q=3$![]() , by (2.2), (2.3) and (2.4),
, by (2.2), (2.3) and (2.4),

It follows that

Thus, we also have $\widetilde {\lambda }_\mu \sim \varepsilon _\mu ^{2}$![]() for $q=3$
for $q=3$![]() . By (1.10) and (2.2),
. By (1.10) and (2.2),

For $3< q<4$![]() , by (2.2), (2.3) and (2.4), $\widetilde {\lambda }_\mu \sim \varepsilon _\mu ^{2}.$
, by (2.2), (2.3) and (2.4), $\widetilde {\lambda }_\mu \sim \varepsilon _\mu ^{2}.$![]() Now, by (1.10),
Now, by (1.10),
Thus, for all $2< q<4$![]() , we always have
, we always have

as $\mu \to 0$![]() . Now, by (2.2)–(2.4) and (2.5), we have
. Now, by (2.2)–(2.4) and (2.5), we have

It follows from (2.2) and (2.6) that

Thus, by (2.6), $\widetilde {v}_{\mu }$![]() is a blow-up solution of (1.4) for $N=3$
is a blow-up solution of (1.4) for $N=3$![]() , $\lambda =1$
, $\lambda =1$![]() , $2< q<4$
, $2< q<4$![]() and $t=\widetilde {t}_\mu$
and $t=\widetilde {t}_\mu$![]() . Note that by [Reference Ma and Moroz25, theorem 2.2], the ground-states of (1.4) for $\lambda =1$
. Note that by [Reference Ma and Moroz25, theorem 2.2], the ground-states of (1.4) for $\lambda =1$![]() , say $\overline {v}_{t}$
, say $\overline {v}_{t}$![]() , satisfies $\|\overline {v}_{t}\|_\infty \sim t^{-\frac {1}{q-2}}$
, satisfies $\|\overline {v}_{t}\|_\infty \sim t^{-\frac {1}{q-2}}$![]() as $t\to +\infty$
as $t\to +\infty$![]() . For $\mu >0$
. For $\mu >0$![]() sufficiently small, $\widetilde {v}_{\mu }$
sufficiently small, $\widetilde {v}_{\mu }$![]() is a second positive radial solution of (1.4) with $N=3$
is a second positive radial solution of (1.4) with $N=3$![]() , $\lambda =1$
, $\lambda =1$![]() , $2< q<4$
, $2< q<4$![]() and $t>0$
and $t>0$![]() sufficiently large.
sufficiently large.
Remark 2.1 Let $\widetilde {v}_\mu$![]() be given in the proof of proposition 2.1 and define
be given in the proof of proposition 2.1 and define
then $\widetilde {w}_{\mu }$![]() satisfies the following equation:
satisfies the following equation:

where $t=\widetilde {t}_\mu$![]() is also given in the proof of proposition 2.1. By similar arguments as that used for [Reference Dávila, del Pino and Guerra14, lemma 5.3], (2.7) has a unique bounded positive radial solution for $t>0$
is also given in the proof of proposition 2.1. By similar arguments as that used for [Reference Dávila, del Pino and Guerra14, lemma 5.3], (2.7) has a unique bounded positive radial solution for $t>0$![]() sufficiently large. However, by (1.10) and (2.5),
sufficiently large. However, by (1.10) and (2.5),

Thus, $\widetilde {w}_{\mu }$![]() is also a blow-up solution of (2.7) as $\widetilde {t}_\mu \to +\infty$
is also a blow-up solution of (2.7) as $\widetilde {t}_\mu \to +\infty$![]() .
.
3. Ground-states for $N=3$ and $2< q\leq 4$
and $2< q\leq 4$
The associated fibering map of (1.6) for every $v\not =0$![]() in $H^{1}(\mathbb {R}^{3})$
in $H^{1}(\mathbb {R}^{3})$![]() is given by
is given by
Since $q>2$![]() , it is standard to show that for every $v\not =0$
, it is standard to show that for every $v\not =0$![]() in $H^{1}(\mathbb {R}^{3})$
in $H^{1}(\mathbb {R}^{3})$![]() , there exists a unique $s_0>0$
, there exists a unique $s_0>0$![]() such that $E(s)$
such that $E(s)$![]() is strictly increasing for $0< s< s_0$
is strictly increasing for $0< s< s_0$![]() and strictly decreasing for $s>s_0$
and strictly decreasing for $s>s_0$![]() .
.
Lemma 3.1 Let $N=3,$![]() $\lambda =1$
$\lambda =1$![]() and $2< q\leq 4$
and $2< q\leq 4$![]() . Then $m(t)=\frac {1}{3}S^{\frac {3}{2}}$
. Then $m(t)=\frac {1}{3}S^{\frac {3}{2}}$![]() for $t>0$
for $t>0$![]() sufficiently small, where $m(t)$
sufficiently small, where $m(t)$![]() is given by (1.5).
is given by (1.5).
Proof. We argue in the contrary by supposing that there exists $t_n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() such that $m(t_n)<\frac {1}{3}S^{\frac {3}{2}}$
such that $m(t_n)<\frac {1}{3}S^{\frac {3}{2}}$![]() . Then, it is standard to show (cf.[Reference Alves, Souto and Montenegro6]) that $m(t_n)$
. Then, it is standard to show (cf.[Reference Alves, Souto and Montenegro6]) that $m(t_n)$![]() is attained by a positive and radial function, which is also a solution of (1.4) with $\lambda =1$
is attained by a positive and radial function, which is also a solution of (1.4) with $\lambda =1$![]() , $N=3$
, $N=3$![]() and $t=t_n$
and $t=t_n$![]() . We denote this solution by $v_{t_n}$
. We denote this solution by $v_{t_n}$![]() . Since $t_n\to 0$
. Since $t_n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , it is also standard to show that
, it is also standard to show that
Thus, $\{v_{t_n}\}$![]() is a minimizing sequence of the Sobolev inequality. By Lions’ result (cf. [Reference Willem34, theorem 1.41]), up to a subsequence, there exists $\sigma _n>0$
is a minimizing sequence of the Sobolev inequality. By Lions’ result (cf. [Reference Willem34, theorem 1.41]), up to a subsequence, there exists $\sigma _n>0$![]() such that for some $\varepsilon _*>0$
such that for some $\varepsilon _*>0$![]() ,
,
Clearly, by direct computations, we know that $w_{t_n}$![]() satisfies the following equation:
satisfies the following equation:
Since $v_{t_n}$![]() is positive and radial, $w_{t_n}$
is positive and radial, $w_{t_n}$![]() is also positive and radial. Thus, by the boundedness of $\{w_{t_n}\}$
is also positive and radial. Thus, by the boundedness of $\{w_{t_n}\}$![]() in $D^{1,2}(\mathbb {R}^{3})$
in $D^{1,2}(\mathbb {R}^{3})$![]() , the Sobolev embedding theorem and Strusss radial lemma (cf. [Reference Berestycki and Lions8, lemma A.2]),
, the Sobolev embedding theorem and Strusss radial lemma (cf. [Reference Berestycki and Lions8, lemma A.2]),
On the other hand, since $w_{t_n}\to U_{\varepsilon _*}$![]() strongly in $D^{1,2}(\mathbb {R}^{3})$
strongly in $D^{1,2}(\mathbb {R}^{3})$![]() as $n\to \infty$
as $n\to \infty$![]() , by applying the Moser iteration in a standard way and using the Sobolev embedding theorem, we know that $w_{t_n}\to U_{\varepsilon _*}$
, by applying the Moser iteration in a standard way and using the Sobolev embedding theorem, we know that $w_{t_n}\to U_{\varepsilon _*}$![]() strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$
strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$![]() as $n\to \infty$
as $n\to \infty$![]() for some $\alpha \in (0, 1)$
for some $\alpha \in (0, 1)$![]() . Thus,
. Thus,
Now, we can adapt the ODE's argument in [Reference Atkinson and Peletier5, Reference Gazzola and Serrin18, Reference Knaap and Peletier21] as that in the proof of [Reference Wei and Wu33, lemma 4.1] to obtain
On the other hand, since $N=3$![]() , it is easy to check that $r^{-1}e^{-\sigma _nr}$
, it is easy to check that $r^{-1}e^{-\sigma _nr}$![]() is a subsolution of $-\Delta u+\sigma _n^{2}u=0$
is a subsolution of $-\Delta u+\sigma _n^{2}u=0$![]() for $r\geq 1$
for $r\geq 1$![]() . Thus, by the fact that $w_{t_n}\to U_{\varepsilon _*}$
. Thus, by the fact that $w_{t_n}\to U_{\varepsilon _*}$![]() strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$
strongly in $C_{loc}^{1,\alpha }(\mathbb {R}^{3})$![]() as $n\to \infty$
as $n\to \infty$![]() for some $\alpha \in (0, 1)$
for some $\alpha \in (0, 1)$![]() , we can use the maximum principle in a standard way to show that
, we can use the maximum principle in a standard way to show that
It follows that

Since $t_n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , by (3.4), for $r\gtrsim (\frac {1}{\sigma _n})^{\frac 12}$
, by (3.4), for $r\gtrsim (\frac {1}{\sigma _n})^{\frac 12}$![]() , (3.3) reads as
, (3.3) reads as
Thus, by (3.4), we can use the maximum principle in a standard way again to obtain

On the other hand, since $\|w_{t_n}\|_6^{6}=\|v_{t_n}\|_6^{6}=S^{\frac {3}{2}}+o_n(1)$![]() , by (3.8) and the Hölder inequality,
, by (3.8) and the Hölder inequality,
which implies
Since $w_{t_n}\to U_{\varepsilon _*}$![]() strongly in $D^{1,2}(\mathbb {R}^{3})$
strongly in $D^{1,2}(\mathbb {R}^{3})$![]() as $n\to \infty$
as $n\to \infty$![]() and $U_{\varepsilon _*}\not \in L^{2}(\mathbb {R}^{3})$
and $U_{\varepsilon _*}\not \in L^{2}(\mathbb {R}^{3})$![]() , by the Fatou lemma,
, by the Fatou lemma,
Thus, by $t_n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() , we have $\sigma _n\to 0$
, we have $\sigma _n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . It follows from (3.4) once more that
. It follows from (3.4) once more that

Thus, by (3.5) and (3.6), we have

Note that as that of (1.8), by the Pohozaev identity, we have
Thus, by (3.7),

which implies

(3.9) contradicts the facts that $t_n,\sigma _n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() for $2< q\leq 4$
for $2< q\leq 4$![]() . It follows that $m(t)\geq \frac {1}{3}S^{\frac {3}{2}}$
. It follows that $m(t)\geq \frac {1}{3}S^{\frac {3}{2}}$![]() for $t>0$
for $t>0$![]() sufficiently small in the case of $2< q\leq 4$
sufficiently small in the case of $2< q\leq 4$![]() . On the other hand, since $m(t)$
. On the other hand, since $m(t)$![]() is the minimum of $\mathcal {E}_t(v)$
is the minimum of $\mathcal {E}_t(v)$![]() on the Nehari manifold $\mathcal {N}_{t}$
on the Nehari manifold $\mathcal {N}_{t}$![]() , it is standard (cf. [Reference Wei and Wu33, lemma 3.3]) to use the fibering maps (3.1) to show that $m(t)$
, it is standard (cf. [Reference Wei and Wu33, lemma 3.3]) to use the fibering maps (3.1) to show that $m(t)$![]() is nonincreasing for $t>0$
is nonincreasing for $t>0$![]() . Note that it is well known that $m(0)=\frac {1}{3}S^{\frac {3}{2}}$
. Note that it is well known that $m(0)=\frac {1}{3}S^{\frac {3}{2}}$![]() , thus, $m(t)\leq \frac {1}{3}S^{\frac {3}{2}}$
, thus, $m(t)\leq \frac {1}{3}S^{\frac {3}{2}}$![]() for all $t>0$
for all $t>0$![]() . It follows that $m(t)=\frac {1}{3}S^{\frac {3}{2}}$
. It follows that $m(t)=\frac {1}{3}S^{\frac {3}{2}}$![]() for $t>0$
for $t>0$![]() sufficiently small in the case of $2< q\leq 4$
sufficiently small in the case of $2< q\leq 4$![]() .
.
Let
Then by lemma 3.1, $t_q^{*}>0$![]() for $2< q\leq 4$
for $2< q\leq 4$![]() . Since it is well known (cf. [Reference Alves, Souto and Montenegro6]) that $m(t)<\frac {1}{3}S^{\frac {3}{2}}$
. Since it is well known (cf. [Reference Alves, Souto and Montenegro6]) that $m(t)<\frac {1}{3}S^{\frac {3}{2}}$![]() for $t>0$
for $t>0$![]() sufficiently large in the case of $2< q\leq 4$
sufficiently large in the case of $2< q\leq 4$![]() , we have $0< t_q^{*}<+\infty$
, we have $0< t_q^{*}<+\infty$![]() for all $2< q\leq 4$
for all $2< q\leq 4$![]() . Since $m(t)<\frac {1}{3}S^{\frac {3}{2}}$
. Since $m(t)<\frac {1}{3}S^{\frac {3}{2}}$![]() for $t>t_q^{*}$
for $t>t_q^{*}$![]() , it is standard (cf. [Reference Alves, Souto and Montenegro6]) to show that $m(t)$
, it is standard (cf. [Reference Alves, Souto and Montenegro6]) to show that $m(t)$![]() is attained for $t>t_q^{*}$
is attained for $t>t_q^{*}$![]() . Let $v_t$
. Let $v_t$![]() be a ground-state of (1.4), which is radial and positive for $t>t_q^{*}$
be a ground-state of (1.4), which is radial and positive for $t>t_q^{*}$![]() in the case of $2< q<4$
in the case of $2< q<4$![]() . Then, we have the following.
. Then, we have the following.
Proposition 3.1 Let $N=3,$![]() $\lambda =1$
$\lambda =1$![]() and $2< q<4$
and $2< q<4$![]() . Then, $\|v_t\|_q^{q}\sim 1$
. Then, $\|v_t\|_q^{q}\sim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() .
.
Proof. The conclusion $\|v_t\|_q^{q}\lesssim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() is standard so we omit it. For the conclusion $\|v_t\|_q^{q}\gtrsim 1$
is standard so we omit it. For the conclusion $\|v_t\|_q^{q}\gtrsim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() , we argue in the contrary. Then there exists $t_n\to t_q^{*}$
, we argue in the contrary. Then there exists $t_n\to t_q^{*}$![]() as $n\to \infty$
as $n\to \infty$![]() such that $\|v_{t_n}\|_q^{q}\to 0$
such that $\|v_{t_n}\|_q^{q}\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() . Similar to that of (3.2), we also have
. Similar to that of (3.2), we also have
Thus, $\{v_{t_n}\}$![]() is a minimizing sequence of the Sobolev inequality. By Lions’ result (cf. [Reference Willem34, theorem 1.41]), up to a subsequence, there exists $\sigma '_n>0$
is a minimizing sequence of the Sobolev inequality. By Lions’ result (cf. [Reference Willem34, theorem 1.41]), up to a subsequence, there exists $\sigma '_n>0$![]() such that for some $\varepsilon _*>0$
such that for some $\varepsilon _*>0$![]() ,
,
Now, repeating the arguments for (3.9), we will arrive at

This is impossible since $\sigma '_n\to 0$![]() as $n\to \infty$
as $n\to \infty$![]() by similar arguments as that used for $\sigma _n$
by similar arguments as that used for $\sigma _n$![]() in the proof of lemma 3.1. Thus, we must have $\|v_t\|_q^{q}\gtrsim 1$
in the proof of lemma 3.1. Thus, we must have $\|v_t\|_q^{q}\gtrsim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() .
.
Now, we are arriving at the following.
Proposition 3.2 Let $\lambda =1,$![]() $N=3$
$N=3$![]() and $2< q\leq 4$
and $2< q\leq 4$![]() . Then
. Then
(1) (1.4) has ground-states for $t\geq t_q^{*}$
 and has no ground-states for $0< t< t_q^{*}$
and has no ground-states for $0< t< t_q^{*}$ in the case of $2< q<4$
in the case of $2< q<4$ .
.(2) (1.4) has ground-states for $t> t_4^{*}$
 and has no ground-states for $0< t< t_4^{*}$
and has no ground-states for $0< t< t_4^{*}$ in the case of $q=4$
in the case of $q=4$ .
.
Here, $t_q^{*}$![]() is given by (3.10).
is given by (3.10).
Proof. We first prove that there is no ground-states of (1.4) for $0< t< t_q^{*}$![]() in the case of $2< q\leq 4$
in the case of $2< q\leq 4$![]() . Suppose the contrary that (1.4) has a ground-state for some $0< t< t_q^{*}$
. Suppose the contrary that (1.4) has a ground-state for some $0< t< t_q^{*}$![]() in the case of $2< q\leq 4$
in the case of $2< q\leq 4$![]() . Then $m(t)$
. Then $m(t)$![]() is attained. Now, by use the fibering maps (3.1) in a standard way (cf. [Reference Wei and Wu33, lemma 3.3]), we have $m(t')< m(t)$
is attained. Now, by use the fibering maps (3.1) in a standard way (cf. [Reference Wei and Wu33, lemma 3.3]), we have $m(t')< m(t)$![]() for all $t'>t$
for all $t'>t$![]() . It follows that $m(t')<\frac {1}{3}S^{\frac {3}{2}}$
. It follows that $m(t')<\frac {1}{3}S^{\frac {3}{2}}$![]() for all $t'>t$
for all $t'>t$![]() , which contradicts the definition of $t_q^{*}$
, which contradicts the definition of $t_q^{*}$![]() given by (3.10). Thus, there is no ground-states of (1.4) for $0< t< t_q^{*}$
given by (3.10). Thus, there is no ground-states of (1.4) for $0< t< t_q^{*}$![]() in the case of $2< q\leq 4$
in the case of $2< q\leq 4$![]() . It remains to prove that (1.4) has a ground-state for $t=t_q^{*}$
. It remains to prove that (1.4) has a ground-state for $t=t_q^{*}$![]() in the case of $2< q<4$
in the case of $2< q<4$![]() , which is equivalent to prove that $m(t_q^{*})$
, which is equivalent to prove that $m(t_q^{*})$![]() is attained for $2< q<4$
is attained for $2< q<4$![]() . Let $v_t$
. Let $v_t$![]() be a ground-state of (1.4), which is radial and positive for $t>t_q^{*}$
be a ground-state of (1.4), which is radial and positive for $t>t_q^{*}$![]() in the case of $2< q<4$
in the case of $2< q<4$![]() such that $t\to t_q^{*}$
such that $t\to t_q^{*}$![]() . By proposition 3.1, $\|v_t\|_q^{q}\gtrsim 1$
. By proposition 3.1, $\|v_t\|_q^{q}\gtrsim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() . Since $v_t$
. Since $v_t$![]() is radial, it is standard to show that $v_t\to v_{t_q^{*}}\not =0$
is radial, it is standard to show that $v_t\to v_{t_q^{*}}\not =0$![]() strongly in $H^{1}(\mathbb {R}^{3})$
strongly in $H^{1}(\mathbb {R}^{3})$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() up to a subsequence. Thus, $m(t_q^{*})$
up to a subsequence. Thus, $m(t_q^{*})$![]() is attained by $v_{t_q^{*}}$
is attained by $v_{t_q^{*}}$![]() , which is also a ground-state of (1.4) for $t=t_q^{*}$
, which is also a ground-state of (1.4) for $t=t_q^{*}$![]() in the case of $2< q<4$
in the case of $2< q<4$![]() .
.
Remark 3.1 Upon to theorem 1.2, the existence of ground-states of (1.4) is almost completely solved, except for $N=3$![]() , $q=4$
, $q=4$![]() and $t=t_4^{*}$
and $t=t_4^{*}$![]() . In this case, we believe that there is no ground-states of (1.4). Indeed, let $\mu >0$
. In this case, we believe that there is no ground-states of (1.4). Indeed, let $\mu >0$![]() , $a>0$
, $a>0$![]() and $(u_\mu, \lambda _\mu )$
and $(u_\mu, \lambda _\mu )$![]() be a normalized solution of (1.7), then by (1.9) and (1.10), $\widetilde {v}_\mu$
be a normalized solution of (1.7), then by (1.9) and (1.10), $\widetilde {v}_\mu$![]() is a solution of (1.4) with $\lambda =1$
is a solution of (1.4) with $\lambda =1$![]() and $t=\widetilde {t}_\mu =\mu \widetilde {\lambda }_\mu ^{\frac {q\gamma _q-q}{2}}$
and $t=\widetilde {t}_\mu =\mu \widetilde {\lambda }_\mu ^{\frac {q\gamma _q-q}{2}}$![]() . By (2.2) and (2.6),
. By (2.2) and (2.6),
Thus, $\widetilde {t}_\mu \to 0$![]() as $\mu \to 0$
as $\mu \to 0$![]() for $4< q<6$
for $4< q<6$![]() and $\widetilde {t}_\mu \sim 1$
and $\widetilde {t}_\mu \sim 1$![]() as $\mu \to 0$
as $\mu \to 0$![]() for $q=4$
for $q=4$![]() . Note that $\widetilde {v}_\mu$
. Note that $\widetilde {v}_\mu$![]() , generated by $\widetilde {u}_\mu$
, generated by $\widetilde {u}_\mu$![]() though (1.9), is a solution of (1.4) for $t=\widetilde {t}_\mu$
though (1.9), is a solution of (1.4) for $t=\widetilde {t}_\mu$![]() and by [Reference Wei and Wu33, theorem 1.2],
and by [Reference Wei and Wu33, theorem 1.2],
It seems that $\widetilde {v}_\mu$![]() will approximate the ground-state level $m(t)=\frac {1}{3}S^{\frac {3}{2}}$
will approximate the ground-state level $m(t)=\frac {1}{3}S^{\frac {3}{2}}$![]() for $N=3$
for $N=3$![]() , ${\lambda =1}$
, ${\lambda =1}$![]() , $q=4$
, $q=4$![]() and $t=t_4^{*}$
and $t=t_4^{*}$![]() as $\mu \to 0$
as $\mu \to 0$![]() , which suggests that the concentration phenomenon will happen at the ground-state level $m(t)=\frac {1}{3}S^{\frac {3}{2}}$
, which suggests that the concentration phenomenon will happen at the ground-state level $m(t)=\frac {1}{3}S^{\frac {3}{2}}$![]() for $N=3$
for $N=3$![]() , $\lambda =1$
, $\lambda =1$![]() , $q=4$
, $q=4$![]() and $t=t_4^{*}$
and $t=t_4^{*}$![]() .
.
We close this section by the proof of theorem 1.2.
4. Normalized ground-states for $2< q<2+4/N$
Let

where $t_q^{*}$![]() is given by (3.10). Then, by [Reference Alves, Souto and Montenegro6, theorem 1.2] and theorem 1.2, (1.4) has a ground-state $v_t$
is given by (3.10). Then, by [Reference Alves, Souto and Montenegro6, theorem 1.2] and theorem 1.2, (1.4) has a ground-state $v_t$![]() for $t>t_q^{**}$
for $t>t_q^{**}$![]() and $2< q<2+\frac {4}{N}$
and $2< q<2+\frac {4}{N}$![]() , which is positive and radial. By (1.11) and (1.12), $(u_t, \lambda _t)$
, which is positive and radial. By (1.11) and (1.12), $(u_t, \lambda _t)$![]() is a positive normalized solution of (1.7) if and only if
is a positive normalized solution of (1.7) if and only if
Clearly, for every $t>t_q^{**}$![]() , there exists a unique
, there exists a unique

such that $F(t,\mu _t)=0$![]() . Let
. Let
Then, (1.7) has a positive normalized solution if and only if $\mu <\overline {\mu }_{q,a}$![]() and $\mu =\mu _t$
and $\mu =\mu _t$![]() . Now, we are prepared for the proof of theorem 1.3.
. Now, we are prepared for the proof of theorem 1.3.
Proof of theorem 1.3. By [Reference Wei and Wu33, theorem 1.1] and [Reference Jeanjean and Le19, theorem 1.6], (1.7) has a normalized ground-state for $\mu >0$![]() sufficiently small. Thus, we only need to prove (1.7) has no normalized ground-states for $\mu >0$
sufficiently small. Thus, we only need to prove (1.7) has no normalized ground-states for $\mu >0$![]() sufficiently large, which is equivalent to show that $\overline {\mu }_{q,a}<+\infty$
sufficiently large, which is equivalent to show that $\overline {\mu }_{q,a}<+\infty$![]() . Recall that $\gamma _q=\frac {N(q-2)}{2q}$
. Recall that $\gamma _q=\frac {N(q-2)}{2q}$![]() , we always have $q>q\gamma _q$
, we always have $q>q\gamma _q$![]() . It follows from (4.2) that $\mu _t\to 0$
. It follows from (4.2) that $\mu _t\to 0$![]() as $t\to t_q^{**}$
as $t\to t_q^{**}$![]() for $N\geq 4$
for $N\geq 4$![]() since $t_q^{**}=0$
since $t_q^{**}=0$![]() for $N\geq 4$
for $N\geq 4$![]() . For $N=3$
. For $N=3$![]() , we have $t_q^{**}=t_q^{*}>0$
, we have $t_q^{**}=t_q^{*}>0$![]() and $\|v_t\|_q^{q}\sim 1$
and $\|v_t\|_q^{q}\sim 1$![]() as $t\to t_q^{*}$
as $t\to t_q^{*}$![]() by proposition 3.1. Thus, $\mu _t\lesssim 1$
by proposition 3.1. Thus, $\mu _t\lesssim 1$![]() as $t\to t_q^{**}$
as $t\to t_q^{**}$![]() for all $N\geq 3$
for all $N\geq 3$![]() . Since $v_t$
. Since $v_t$![]() is a ground-state of (1.4) with the least energy $m(t)$
is a ground-state of (1.4) with the least energy $m(t)$![]() on the Nehari manifold $\mathcal {N}_t$
on the Nehari manifold $\mathcal {N}_t$![]() , by standard arguments (cf. [Reference Chen and Zou11, lemma 2.2]),
, by standard arguments (cf. [Reference Chen and Zou11, lemma 2.2]),

and
As that of (1.8), by the Pohozaev identity, we have
which implies $m(t)t^{\frac {N}{q\gamma _q}}$![]() is increasing for $t>t_q^{**}$
is increasing for $t>t_q^{**}$![]() . Now, let $t_0>t_q^{**}$
. Now, let $t_0>t_q^{**}$![]() with $t_0-t_q^{**}>0$
with $t_0-t_q^{**}>0$![]() sufficiently small such that $\mu _t\lesssim 1$
sufficiently small such that $\mu _t\lesssim 1$![]() for $t< t_0$
for $t< t_0$![]() , then
, then
On the other hand, by the definition of $t_q^{**}$![]() given by (4.1), [Reference Alves, Souto and Montenegro6, theorem 1.2] and theorem 1.2, $m(t)<\frac {1}{N}S^{\frac {N}{2}}$
given by (4.1), [Reference Alves, Souto and Montenegro6, theorem 1.2] and theorem 1.2, $m(t)<\frac {1}{N}S^{\frac {N}{2}}$![]() for $t>t_q^{**}$
for $t>t_q^{**}$![]() . Thus, it is standard to apply the classical elliptic estimates to show that $\|v_t\|_\infty \lesssim 1$
. Thus, it is standard to apply the classical elliptic estimates to show that $\|v_t\|_\infty \lesssim 1$![]() for all $t\geq t_0$
for all $t\geq t_0$![]() . By (4.4) and (4.5),
. By (4.4) and (4.5),

which implies that for every $\varepsilon >0$![]() there exists $t_\varepsilon >0$
there exists $t_\varepsilon >0$![]() such that $m(t)\lesssim t^{-\frac {N}{q\gamma _q+\varepsilon }}$
such that $m(t)\lesssim t^{-\frac {N}{q\gamma _q+\varepsilon }}$![]() for $t\geq t_\varepsilon$
for $t\geq t_\varepsilon$![]() . It follows from (4.5) once more that
. It follows from (4.5) once more that
Thus, by (4.5) and $\|v_t\|_\infty \lesssim 1$![]() for all $t\geq t_0$
for all $t\geq t_0$![]() , we have
, we have
which implies $m(t)t^{\frac {N}{q\gamma _q}}-C_1t^{-\frac {N}{q\gamma _q+\varepsilon }}$![]() is decreasing for $t\geq t_\varepsilon$
is decreasing for $t\geq t_\varepsilon$![]() . Therefore, $m(t)\lesssim t^{-\frac {N}{q\gamma _q}}$
. Therefore, $m(t)\lesssim t^{-\frac {N}{q\gamma _q}}$![]() for $t>0$
for $t>0$![]() sufficiently large, which, together with (4.6), implies that
sufficiently large, which, together with (4.6), implies that
It follows from (4.5) and $\|v_t\|_\infty \lesssim 1$![]() for all $t\geq t_0$
for all $t\geq t_0$![]() that
that
Since
by (4.2), $\overline {\mu }_{q,a}<+\infty$![]() for $2< q<2+\frac {4}{N}$
for $2< q<2+\frac {4}{N}$![]() .
.
5. An application
In this section, we shall apply our above strategy to study the Schrödinger equation (1.15). Since there is an additional condition $\|u\|_2^{2}=r^{2}$![]() in (1.15), $\lambda$
in (1.15), $\lambda$![]() in (1.15) is not fixed but appears as a Lagrange multiplier.
in (1.15) is not fixed but appears as a Lagrange multiplier.
Let $(u_r, \lambda _r)$![]() be a solution of (1.15). Since $V(x)=x_1^{2}+x_2^{2}$
be a solution of (1.15). Since $V(x)=x_1^{2}+x_2^{2}$![]() , we have $\nabla V(x)\cdot x=2V(x)$
, we have $\nabla V(x)\cdot x=2V(x)$![]() . Thus, the Pohozaev identity of (1.15) (cf. [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7]) is given by
. Thus, the Pohozaev identity of (1.15) (cf. [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7]) is given by
which, combining the equation (1.15), implies that
We define
Then by $V(x)=x_1^{2}+x_2^{2}$![]() and (5.1), $(w_r, t_r)$
and (5.1), $(w_r, t_r)$![]() is a solution of the following equation:
is a solution of the following equation:

Clearly, if $(w_r, t_r)$![]() is a solution of (5.3), then, by (5.2), $(u_r, \lambda _r)$
is a solution of (5.3), then, by (5.2), $(u_r, \lambda _r)$![]() is also a solution of (1.15).
is also a solution of (1.15).
With these basic observations in hands, to find normalized solutions of (1.15) with positive Lagrange multipliers, it is equivalent to study the existence of solutions of (5.3). For this purpose, let us first consider the following equation:

The corresponding functional of (5.4) is given by
By [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1] and the Sobolev embedding theorem, this functional is well defined and of class $C^{2}$![]() in the Hilbert space
in the Hilbert space
with the norm

We also define the usual Nehari manifold of $\mathcal {J}_t(w)$![]() as follows:
as follows:
The associated fibering map for every $w\not =0$![]() in $X$
in $X$![]() is given by
is given by
Since $p>2$![]() , it is standard to show that for every $w\not =0$
, it is standard to show that for every $w\not =0$![]() in $X$
in $X$![]() , there exists a unique $s_0'>0$
, there exists a unique $s_0'>0$![]() such that $J(s)$
such that $J(s)$![]() is strictly increasing for $0< s< s_0'$
is strictly increasing for $0< s< s_0'$![]() and is strictly decreasing for $s>s_0'$
and is strictly decreasing for $s>s_0'$![]() . Let
. Let
Definition 5.1 We say that $w$![]() is a ground-state of (5.4) if $w$
is a ground-state of (5.4) if $w$![]() is a nontrivial solution of (5.4) with $\mathcal {J}_t(w)=\mathfrak {m}(t)$
is a nontrivial solution of (5.4) with $\mathcal {J}_t(w)=\mathfrak {m}(t)$![]() .
.
We also need the following equation:

The corresponding functional of (5.7) is given by
This functional is well defined and of class $C^{2}$![]() in the Hilbert space $X$
in the Hilbert space $X$![]() , which is given by (5.5). We define the usual Nehari manifold of $\mathcal {I}_t(u)$
, which is given by (5.5). We define the usual Nehari manifold of $\mathcal {I}_t(u)$![]() by
by
The associated fibering map for every $u\not =0$![]() in $X$
in $X$![]() is given by
is given by
Since $p>2$![]() , it is standard to show that for every $u\not =0$
, it is standard to show that for every $u\not =0$![]() in $X$
in $X$![]() , there exists a unique $s_*>0$
, there exists a unique $s_*>0$![]() such that $I(s)$
such that $I(s)$![]() is strictly increasing for $0< s< s_*$
is strictly increasing for $0< s< s_*$![]() and is strictly decreasing for $s>s_*$
and is strictly decreasing for $s>s_*$![]() . Let
. Let
Definition 5.2 We say that $u$![]() is a ground-state of (5.7) if $u$
is a ground-state of (5.7) if $u$![]() is a nontrivial solution of (5.7) with $\mathcal {I}_t(u)=\mathbb {M}(t)$
is a nontrivial solution of (5.7) with $\mathcal {I}_t(u)=\mathbb {M}(t)$![]() .
.
Now, we have the following result of (5.4).
Proposition 5.1 Let $\frac {10}{3}< p<6$![]() , then (5.4) has a positive ground-state $w_t$
, then (5.4) has a positive ground-state $w_t$![]() for all $t>0$
for all $t>0$![]() satisfying $\|w_t\|_2^{2}\sim t^{\frac {3p-10}{2(p-2)}}$
satisfying $\|w_t\|_2^{2}\sim t^{\frac {3p-10}{2(p-2)}}$![]() as $t\to 0$
as $t\to 0$![]() and $w_t\to w_\infty$
and $w_t\to w_\infty$![]() strongly in $H^{1}(\mathbb {R}^{3})$
strongly in $H^{1}(\mathbb {R}^{3})$![]() as $t\to +\infty,$
as $t\to +\infty,$![]() where $w_\infty$
where $w_\infty$![]() is the unique (up to translations) positive solution of the following equation:
is the unique (up to translations) positive solution of the following equation:

Moreover, $w_t$![]() is unique for $t>0$
is unique for $t>0$![]() sufficiently large.
sufficiently large.
Proof. The proof is standard so we only sketch it here. We first prove the existence of ground-states of (5.4). By the discussion in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, 4.2 Symmetry of minimizers], we know that for the energy level $\mathfrak {m}(t)$![]() , there exists a minimizing sequence $\{w_n\}$
, there exists a minimizing sequence $\{w_n\}$![]() on the Nehari manifold $\mathcal {M}_t$
on the Nehari manifold $\mathcal {M}_t$![]() such that $w_n$
such that $w_n$![]() is real and positive. Moreover, $w_n$
is real and positive. Moreover, $w_n$![]() is radial and decreasing w.r.t. $(x_1, x_2)$
is radial and decreasing w.r.t. $(x_1, x_2)$![]() for all $x_3$
for all $x_3$![]() and $w_n$
and $w_n$![]() is even and decreasing w.r.t. $x_3$
is even and decreasing w.r.t. $x_3$![]() for all $(x_1, x_2)$
for all $(x_1, x_2)$![]() . Since $\frac {10}{3}< p<6$
. Since $\frac {10}{3}< p<6$![]() , it is standard to use the fibering maps (5.6) to show that $\mathfrak {m}(t)>0$
, it is standard to use the fibering maps (5.6) to show that $\mathfrak {m}(t)>0$![]() on $\mathcal {M}_t$
on $\mathcal {M}_t$![]() . Thus, by [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 3.4], there exists $\{z_n\}\in \mathbb {R}$
. Thus, by [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 3.4], there exists $\{z_n\}\in \mathbb {R}$![]() such that
such that
Since $\frac {10}{3}< p<6$![]() , the fibering map of every $w\not =0$
, the fibering map of every $w\not =0$![]() in $X$
in $X$![]() , see (5.6), has a unique maximum point $s_0'$
, see (5.6), has a unique maximum point $s_0'$![]() and it interacts the Nehari manifold $\mathcal {M}_t$
and it interacts the Nehari manifold $\mathcal {M}_t$![]() only at the unique maximum point $s_0'$
only at the unique maximum point $s_0'$![]() . Thus, we can use standard arguments (cf. [Reference Wei and Wu33, proposition 3.1]) to show that $w_0$
. Thus, we can use standard arguments (cf. [Reference Wei and Wu33, proposition 3.1]) to show that $w_0$![]() is a positive ground-state of (5.4). We next prove the convergent conclusion for $t\to +\infty$
is a positive ground-state of (5.4). We next prove the convergent conclusion for $t\to +\infty$![]() . Let $w_t$
. Let $w_t$![]() be a positive ground-state of (5.4) for $t>0$
be a positive ground-state of (5.4) for $t>0$![]() . Since $V(x)\geq 0$
. Since $V(x)\geq 0$![]() , $t>0$
, $t>0$![]() and $w_t$
and $w_t$![]() is positive, we know that $w_t$
is positive, we know that $w_t$![]() satisfies
satisfies
By using the fibering maps (5.6) in a standard way (cf. [Reference Wei and Wu33, lemma 3.2]), we know that $\mathfrak {m}(t)$![]() is decreasing w.r.t. $t>0$
is decreasing w.r.t. $t>0$![]() . Thus, $\{w_t\}$
. Thus, $\{w_t\}$![]() is bounded in $H^{1}(\mathbb {R}^{3})$
is bounded in $H^{1}(\mathbb {R}^{3})$![]() . It follows from (5.10) and the classical elliptic estimates that
. It follows from (5.10) and the classical elliptic estimates that
Thus, by $V(x)=x_1^{2}+x_2^{2}$![]() ,
,
which implies that
Now, using the fibering maps (5.6) in a standard way, we know that $\mathfrak {m}(t)\geq \mathfrak {m}+o_t(1)$![]() as $t\to +\infty$
as $t\to +\infty$![]() , where
, where
with
and
On the other hand, it is well known that (5.9) has a unique (up to translations) positive radial solution $w_\infty$![]() , which exponentially decays to zero at infinity. Thus, using $w_\infty$
, which exponentially decays to zero at infinity. Thus, using $w_\infty$![]() as a test function and adapting the property of the fibering maps (5.6) in a standard way, we also have $\mathfrak {m}(t)\leq \mathfrak {m}+o_t(1)$
as a test function and adapting the property of the fibering maps (5.6) in a standard way, we also have $\mathfrak {m}(t)\leq \mathfrak {m}+o_t(1)$![]() as $t\to +\infty$
as $t\to +\infty$![]() . It follows that $\mathfrak {m}(t)=\mathfrak {m}+o_t(1)$
. It follows that $\mathfrak {m}(t)=\mathfrak {m}+o_t(1)$![]() as $t\to +\infty$
as $t\to +\infty$![]() , which implies that $\|w_t\|_p^{p}=\|w_\infty \|_p^{p}+o_t(1)$
, which implies that $\|w_t\|_p^{p}=\|w_\infty \|_p^{p}+o_t(1)$![]() . Now, by standard arguments and the uniqueness of $w_\infty$
. Now, by standard arguments and the uniqueness of $w_\infty$![]() , we can show that $w_t\to w_\infty$
, we can show that $w_t\to w_\infty$![]() strongly in $H^{1}(\mathbb {R}^{3})$
strongly in $H^{1}(\mathbb {R}^{3})$![]() as $t\to +\infty$
as $t\to +\infty$![]() . We now turn to the proof of the convergent conclusion for $t\to 0$
. We now turn to the proof of the convergent conclusion for $t\to 0$![]() . For every $t>0$
. For every $t>0$![]() , let $w_t$
, let $w_t$![]() be a positive ground-state of (5.4), then by (5.2), $u_t$
be a positive ground-state of (5.4), then by (5.2), $u_t$![]() is a positive solution of (5.7). Moreover, by direct calculations,
is a positive solution of (5.7). Moreover, by direct calculations,
Thus, $u_t$![]() is a positive ground-state of (5.7) for all $t>0$
is a positive ground-state of (5.7) for all $t>0$![]() . On the other hand, by [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1], Hölder and Sobolev inequalities,
. On the other hand, by [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1], Hölder and Sobolev inequalities,
Thus, by using the fibering maps (5.8) in a standard way, we know that $\mathbb {M}(0)>0$![]() . By similar arguments as that used above to compare the energy levels $\mathbb {M}(0)$
. By similar arguments as that used above to compare the energy levels $\mathbb {M}(0)$![]() and $\mathbb {M}(t)$
and $\mathbb {M}(t)$![]() , we can obtain that $\mathbb {M}(t)=\mathbb {M}(0)+o_t(1)$
, we can obtain that $\mathbb {M}(t)=\mathbb {M}(0)+o_t(1)$![]() as $t\to 0$
as $t\to 0$![]() . It follows that $\{u_t\}$
. It follows that $\{u_t\}$![]() is bounded in $X$
is bounded in $X$![]() and $\|u_t\|_p^{p}\sim 1$
and $\|u_t\|_p^{p}\sim 1$![]() as $t\to 0$
as $t\to 0$![]() . By [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1], $\{u_t\}$
. By [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1], $\{u_t\}$![]() is also bounded in $H^{1}(\mathbb {R}^{3})$
is also bounded in $H^{1}(\mathbb {R}^{3})$![]() as $t\to 0$
as $t\to 0$![]() . Now, by the Lions’ lemma (cf. [Reference Lions23, lemma I.1] or [Reference Willem34, lemma 1.21]), we can conclude that $\|u_t\|_2^{2}\sim 1$
. Now, by the Lions’ lemma (cf. [Reference Lions23, lemma I.1] or [Reference Willem34, lemma 1.21]), we can conclude that $\|u_t\|_2^{2}\sim 1$![]() as $t\to 0$
as $t\to 0$![]() . It follows from (5.2) that $\|w_t\|_2^{2}\sim t^{\frac {3p-10}{2(p-2)}}$
. It follows from (5.2) that $\|w_t\|_2^{2}\sim t^{\frac {3p-10}{2(p-2)}}$![]() as $t\to 0$
as $t\to 0$![]() . We close this proof by showing the uniqueness of $w_t$
. We close this proof by showing the uniqueness of $w_t$![]() for $t>0$
for $t>0$![]() sufficiently large. Let $w_t$
sufficiently large. Let $w_t$![]() and $w_t'$
and $w_t'$![]() be two different positive ground-states of (5.4) and we define $\phi _t=\frac {w_t-w_t'}{\|w_t-w_t'\|_{L^{\infty }}(\mathbb {R}^{3})}$
be two different positive ground-states of (5.4) and we define $\phi _t=\frac {w_t-w_t'}{\|w_t-w_t'\|_{L^{\infty }}(\mathbb {R}^{3})}$![]() . Then by the Taylor expansion,
. Then by the Taylor expansion,
where $\theta \in (0, 1)$![]() . Since $V(x)\geq 0$
. Since $V(x)\geq 0$![]() , by (5.11),
, by (5.11),
Thus, by the maximum principle, $|\phi _t|\lesssim e^{-\frac {1}{2}|x|}$![]() for $|x|\geq 1$
for $|x|\geq 1$![]() . It is standard to show that $\phi _t\to \phi$
. It is standard to show that $\phi _t\to \phi$![]() strongly in any compact sets as $t\to +\infty$
strongly in any compact sets as $t\to +\infty$![]() and
and
Note that $w_t$![]() and $w_t'$
and $w_t'$![]() are radial w.r.t. $(x_1, x_2)$
are radial w.r.t. $(x_1, x_2)$![]() for all $x_3$
for all $x_3$![]() and even w.r.t. $x_3$
and even w.r.t. $x_3$![]() for all $(x_1, x_2)$
for all $(x_1, x_2)$![]() . Thus, $\phi _t$
. Thus, $\phi _t$![]() is also radial w.r.t. $(x_1, x_2)$
is also radial w.r.t. $(x_1, x_2)$![]() for all $x_3$
for all $x_3$![]() and even w.r.t. $x_3$
and even w.r.t. $x_3$![]() for all $(x_1, x_2)$
for all $(x_1, x_2)$![]() . Now, by the well-known nondegeneracy of $w_\infty$
. Now, by the well-known nondegeneracy of $w_\infty$![]() , we have $\phi _\infty \equiv 0$
, we have $\phi _\infty \equiv 0$![]() . It, together with $|\phi _t|\lesssim e^{-\frac {1}{2}|x|}$
. It, together with $|\phi _t|\lesssim e^{-\frac {1}{2}|x|}$![]() for $|x|\geq 1$
for $|x|\geq 1$![]() , contradicts $\|\phi _t\|_{L^{\infty }(\mathbb {R}^{3})}=1$
, contradicts $\|\phi _t\|_{L^{\infty }(\mathbb {R}^{3})}=1$![]() . Therefore, $w_t$
. Therefore, $w_t$![]() is unique for $t>0$
is unique for $t>0$![]() sufficiently large.
sufficiently large.
Let $w_t$![]() be a positive ground-state of (5.4) given by proposition 5.1 and we define
be a positive ground-state of (5.4) given by proposition 5.1 and we define
By proposition 5.1, for every $t>0$![]() sufficiently large, there exists a unique
sufficiently large, there exists a unique

such that $f(r_t,t)=0$![]() . Thus, by (5.2), $(u_{r_t}, t)$
. Thus, by (5.2), $(u_{r_t}, t)$![]() is a positive normalized solution of (1.15) with a positive Lagrange multiplier $t>0$
is a positive normalized solution of (1.15) with a positive Lagrange multiplier $t>0$![]() . We are now prepared for the proof of theorem 1.4.
. We are now prepared for the proof of theorem 1.4.
Proof of theorem 1.4. By the uniqueness of $w_t$![]() given by proposition 5.1 for $t>0$
given by proposition 5.1 for $t>0$![]() sufficiently large, say $t>T_*$
sufficiently large, say $t>T_*$![]() . It is standard to show that $\int _{\mathbb {R}^{3}}V(x)w_t^{2}$
. It is standard to show that $\int _{\mathbb {R}^{3}}V(x)w_t^{2}$![]() is continuous for $t>T_*$
is continuous for $t>T_*$![]() . Note that by proposition 5.1,
. Note that by proposition 5.1,
Thus, by $\frac {10}{3}< p<6$![]() , for every $r<(T_*^{\frac {10-3p}{2(p-2)}}(\tfrac {6-p}{2p}\|w_{T_*}\|_p^{p}-2T_*^{-2}\int _{\mathbb {R}^{3}}V(x)w_{T_*}^{2}{\rm d}x))^{\frac {1}{2}}$
, for every $r<(T_*^{\frac {10-3p}{2(p-2)}}(\tfrac {6-p}{2p}\|w_{T_*}\|_p^{p}-2T_*^{-2}\int _{\mathbb {R}^{3}}V(x)w_{T_*}^{2}{\rm d}x))^{\frac {1}{2}}$![]() , $f(r,t)=0$
, $f(r,t)=0$![]() has a solution $t_r>T_*$
has a solution $t_r>T_*$![]() . This, together with [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, theorem 2], implies that (1.15) has a second positive normalized solution $u_{r,2}$
. This, together with [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, theorem 2], implies that (1.15) has a second positive normalized solution $u_{r,2}$![]() with a positive Lagrange multiplier $\lambda _{r,2}$
with a positive Lagrange multiplier $\lambda _{r,2}$![]() . The asymptotic behaviour of $u_{r,2}$
. The asymptotic behaviour of $u_{r,2}$![]() and $\lambda _{r,2}$
and $\lambda _{r,2}$![]() is obtained by (5.2) and (5.13). It remains to show that $u_{r,2}$
is obtained by (5.2) and (5.13). It remains to show that $u_{r,2}$![]() is a mountain-pass solution of (1.15) for $r>0$
is a mountain-pass solution of (1.15) for $r>0$![]() sufficiently small. As that in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, remark 1.10], we introduce the mountain-pass level
sufficiently small. As that in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, remark 1.10], we introduce the mountain-pass level
where $\mathcal {Y}(u)=\frac {1}{2}\|u\|_{X}^{2}-\frac {1}{p}\|u\|_p^{p}$![]() and
and
with $u_{r,1}$![]() being a local minimizer of $\mathcal {Y}(u)$
being a local minimizer of $\mathcal {Y}(u)$![]() in $\mathcal {S}_r$
in $\mathcal {S}_r$![]() found in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7] and $\mathcal {S}_r=\{u\in X\mid \|u\|_2^{2}=r^{2}\}$
found in [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7] and $\mathcal {S}_r=\{u\in X\mid \|u\|_2^{2}=r^{2}\}$![]() . Let
. Let
where $\|u\|_{X,t}$![]() is a norm in $X$
is a norm in $X$![]() given by
given by

Then by [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, lemma 2.1] and the Sobolev inequality, for a fixed $\rho >0$![]() sufficiently small, it can be proved by using $\frac {10}{3}< p<6$
sufficiently small, it can be proved by using $\frac {10}{3}< p<6$![]() in a standard way that
in a standard way that
where
Now, for every $g[s]\in \Gamma _r$![]() , we define $g^{*}[s]=\lambda _{r,2}^{-\frac {1}{p-2}}g[s](\lambda _{r,2}^{-\frac {1}{2}}x)$
, we define $g^{*}[s]=\lambda _{r,2}^{-\frac {1}{p-2}}g[s](\lambda _{r,2}^{-\frac {1}{2}}x)$![]() . Then
. Then
By [Reference Bellazzini, Boussaid, Jeanjean and Visciglia7, theorem 1] and (1.16),
Thus, $g^{*}[0]\in B_{\rho,X,\lambda _{r,2}}$![]() for $r>0$
for $r>0$![]() sufficiently small and $\mathcal {J}_t(g^{*}[0])\to 0$
sufficiently small and $\mathcal {J}_t(g^{*}[0])\to 0$![]() as $r\to 0$
as $r\to 0$![]() . By the definition of $g[t]$
. By the definition of $g[t]$![]() , we also have $\mathcal {J}_t(g^{*}[1])<\frac {1}{4}\rho ^{2}$
, we also have $\mathcal {J}_t(g^{*}[1])<\frac {1}{4}\rho ^{2}$![]() . It follows that $g^{*}[t]\in \Theta$
. It follows that $g^{*}[t]\in \Theta$![]() , which implies
, which implies
On the other hand, the fibering map of $\mathcal {Y}(u)$![]() at $u_{r,2}$
at $u_{r,2}$![]() is given by
is given by
By direct calculations,
and
Clearly, $\mathcal {T}_{u_{r,2}}'(1)=0$![]() . Moreover, by (1.18), (5.12) and the Pohozaev identity of $w_\infty$
. Moreover, by (1.18), (5.12) and the Pohozaev identity of $w_\infty$![]() ,
,
for $r>0$![]() sufficiently small. Now, let $h(\tau )=\tau ^{4}\|\nabla u_{r,2}\|_2^{2}-\gamma _p\tau ^{p\gamma _p+2}\|u_{r,2}\|_p^{p},$
sufficiently small. Now, let $h(\tau )=\tau ^{4}\|\nabla u_{r,2}\|_2^{2}-\gamma _p\tau ^{p\gamma _p+2}\|u_{r,2}\|_p^{p},$![]() then,
then,

It follows that there exists $\tau _r<1$![]() such that $\mathcal {T}_{u_{r,2}}'(\tau _r)=0$
such that $\mathcal {T}_{u_{r,2}}'(\tau _r)=0$![]() and $\mathcal {T}_{u_{r,2}}''(\tau _r)>0$
and $\mathcal {T}_{u_{r,2}}''(\tau _r)>0$![]() . We claim that $\tau _r\to 0$
. We claim that $\tau _r\to 0$![]() as $r\to 0$
as $r\to 0$![]() . If not, then, there exists $r_n\to 0$
. If not, then, there exists $r_n\to 0$![]() such that $\tau _{r_n}\gtrsim 1$
such that $\tau _{r_n}\gtrsim 1$![]() as $n\to \infty$
as $n\to \infty$![]() . Without loss of generality, we may assume $\tau _r\gtrsim 1$
. Without loss of generality, we may assume $\tau _r\gtrsim 1$![]() for all $r>0$
for all $r>0$![]() sufficiently small. By $\mathcal {T}_{u_{r,2}}'(\tau _{r})=0$
sufficiently small. By $\mathcal {T}_{u_{r,2}}'(\tau _{r})=0$![]() , (1.18), (5.12) and the Pohozaev identity of $w_\infty$
, (1.18), (5.12) and the Pohozaev identity of $w_\infty$![]() ,
,

which implies $\tau _r<(\tfrac {4}{p\gamma _p+2})^{\frac {1}{p\gamma _p-2}}<1$![]() . Without loss of generality, we may assume that $\tau _r\to \tau _0$
. Without loss of generality, we may assume that $\tau _r\to \tau _0$![]() as $r\to 0$
as $r\to 0$![]() . Then by $\mathcal {T}_{u_{r,2}}'(\tau _r)=0$
. Then by $\mathcal {T}_{u_{r,2}}'(\tau _r)=0$![]() , (5.12) and the fact that $w_\infty$
, (5.12) and the fact that $w_\infty$![]() solves (1.17), we must have $\tau _0=0$
solves (1.17), we must have $\tau _0=0$![]() . It is impossible. Thus, we must have $\tau _r\to 0$
. It is impossible. Thus, we must have $\tau _r\to 0$![]() as $r\to 0$
as $r\to 0$![]() . By (1.16) and (1.18),
. By (1.16) and (1.18),
It follows from (1.16) and (1.18) that
as $r\to 0$![]() , where $(u_{r,2})_{\tau _r}=\tau _r^{\frac {3}{2}}u_{r,2}(\tau _r x)$
, where $(u_{r,2})_{\tau _r}=\tau _r^{\frac {3}{2}}u_{r,2}(\tau _r x)$![]() . Thus, $(u_{r,2})_{\tau _r}\in B_{r\chi,X,1}$
. Thus, $(u_{r,2})_{\tau _r}\in B_{r\chi,X,1}$![]() for a fixed and large $\chi >0$
for a fixed and large $\chi >0$![]() . Since $B_{r\chi,X,1}$
. Since $B_{r\chi,X,1}$![]() is connected, we can find a continuous path $\Upsilon : [0, 1]$
is connected, we can find a continuous path $\Upsilon : [0, 1]$![]() with $\Upsilon (0)=u_{r,1}$
with $\Upsilon (0)=u_{r,1}$![]() and $\Upsilon (1)=(u_{r,2})_{\tau _r}$
and $\Upsilon (1)=(u_{r,2})_{\tau _r}$![]() . Now, we define
. Now, we define

where we choose $\tau _{r,*}>1$![]() such that $\mathcal {T}_{u_{r,2}}(\tau _{r,*})<\mathcal {Y}(u_{r,1})$
such that $\mathcal {T}_{u_{r,2}}(\tau _{r,*})<\mathcal {Y}(u_{r,1})$![]() . Note that $\mathcal {Y}(u)\lesssim r^{2}$
. Note that $\mathcal {Y}(u)\lesssim r^{2}$![]() in $B_{r\chi,X,1}$
in $B_{r\chi,X,1}$![]() and $\mathcal {Y}(u_{r,2})\gtrsim 1$
and $\mathcal {Y}(u_{r,2})\gtrsim 1$![]() by (1.16) and (1.18). Thus, for $r>0$
by (1.16) and (1.18). Thus, for $r>0$![]() sufficiently small, $h^{**}[s]\in \Gamma _r$
sufficiently small, $h^{**}[s]\in \Gamma _r$![]() and
and
Therefore, $\mathfrak {m}(\lambda _{r,2})\lambda _{r,2}^{\frac {6-p}{2(p-2)}}-\frac {\lambda _{r,2}r^{2}}{2}=\alpha (r)$![]() and $u_{r,2}$
and $u_{r,2}$![]() is a mountain-pass solution of (1.15) for $r>0$
is a mountain-pass solution of (1.15) for $r>0$![]() sufficiently small.
sufficiently small.
Acknowledgments
The research of J. Wei is partially supported by NSERC of Canada and the research of Y. Wu is supported by NSFC (No. 11971339, 12171470).