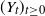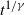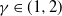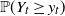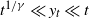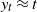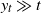1. Introduction: Telecom processes
1.1. A service system
Telecom processes originate from a remarkable work by I. Kaj and M. S. Taqqu [Reference Kaj and Taqqu9], who handled the limit behavior of ‘teletraffic systems’ by using the language of integral representations as a unifying technique. Their article represented a wave of interest in the subject; see, e.g., [Reference Kaj, Leskelä, Norros and Schmidt8, Reference Kurtz10, Reference Pipiras and Taqqu12, Reference Rosenkrantz and Horowitz13, Reference Taqqu14], and the surveys with further references [Reference Kaj5, Reference Kaj6, Reference Kaj7], to mention just a few. The simplicity of the dependence mechanism used in the model enables us to get a clear understanding both of long-range dependence in one case, and independent increments in other cases.
The work of the system represents a collection of service processes or sessions, using telecommunication terminology. Every process starts at some time s, lasts u units of time, and occupies r resource units (synonyms for resource are reward, transmission rate, etc.). The amount of occupied resources r remains constant during every service process.
The formal model of the service system is based on Poisson random measures. Let
![]() $\mathcal R\;:\!=\;\{(s,u,r)\}= {\mathbb R} \times {\mathbb R}_+\times {\mathbb R}_+$
. Every point (s, u, r) corresponds to a possible service process with starting time s, duration u, and required resources r.
$\mathcal R\;:\!=\;\{(s,u,r)\}= {\mathbb R} \times {\mathbb R}_+\times {\mathbb R}_+$
. Every point (s, u, r) corresponds to a possible service process with starting time s, duration u, and required resources r.
The system is characterized by the following parameters:
 $\lambda>0$
: the arrival intensity of service processes;
$\lambda>0$
: the arrival intensity of service processes; $F_U({\textrm{d}} u)$
: the distribution of service duration;
$F_U({\textrm{d}} u)$
: the distribution of service duration; $F_R({\textrm{d}} r)$
: the distribution of the amount of resources required.
$F_R({\textrm{d}} r)$
: the distribution of the amount of resources required.
We can assume that
![]() ${\mathbb P}(R>0)={\mathbb P}(U>0)=1$
without loss of generality.
${\mathbb P}(R>0)={\mathbb P}(U>0)=1$
without loss of generality.
Define on
![]() $\mathcal R$
an intensity measure
$\mathcal R$
an intensity measure
![]() $\mu({\textrm{d}} s,{\textrm{d}} u,{\textrm{d}} r)\;:\!=\; \lambda {\textrm{d}} s\, F_U({\textrm{d}} u)\, F_R({\textrm{d}} r)$
. Let N be a Poisson random measure with intensity
$\mu({\textrm{d}} s,{\textrm{d}} u,{\textrm{d}} r)\;:\!=\; \lambda {\textrm{d}} s\, F_U({\textrm{d}} u)\, F_R({\textrm{d}} r)$
. Let N be a Poisson random measure with intensity
![]() $\mu$
. We can consider the samples of N (sets of triplets (s, u, r), each triplet corresponding to a service process) as variants (sample paths) of the work for the system.
$\mu$
. We can consider the samples of N (sets of triplets (s, u, r), each triplet corresponding to a service process) as variants (sample paths) of the work for the system.
The instant workload of the system at time t is
![]() $W^\circ(t) \;:\!=\; \int_\mathcal R r { {\mathbf 1}_{ \{{s\le t\le s+u} \}}} \, {\textrm{d}} N$
. This is essentially the sum of occupied resources over the processes active at time t. The integral workload over the interval [0, t] is
$W^\circ(t) \;:\!=\; \int_\mathcal R r { {\mathbf 1}_{ \{{s\le t\le s+u} \}}} \, {\textrm{d}} N$
. This is essentially the sum of occupied resources over the processes active at time t. The integral workload over the interval [0, t] is
 \begin{align*} W^*(t) & \;:\!=\; \int_0^t W^\circ(\tau){\textrm{d}}\tau = \int_\mathcal R r \int_0^t { {\mathbf 1}_{ \{{s\le \tau \le s+u} \}}} \, {\textrm{d}}\tau \, {\textrm{d}} N \\[5pt] & = \int_\mathcal R r\cdot \big| [s,s+u]\cap[0,t] \big| \, {\textrm{d}} N \;:\!=\; \int_\mathcal R r \ell_t(s,u) \, {\textrm{d}} N.\end{align*}
\begin{align*} W^*(t) & \;:\!=\; \int_0^t W^\circ(\tau){\textrm{d}}\tau = \int_\mathcal R r \int_0^t { {\mathbf 1}_{ \{{s\le \tau \le s+u} \}}} \, {\textrm{d}}\tau \, {\textrm{d}} N \\[5pt] & = \int_\mathcal R r\cdot \big| [s,s+u]\cap[0,t] \big| \, {\textrm{d}} N \;:\!=\; \int_\mathcal R r \ell_t(s,u) \, {\textrm{d}} N.\end{align*}
Here,
![]() $|\!\cdot\!|$
stands for the length of an interval, and the kernel
$|\!\cdot\!|$
stands for the length of an interval, and the kernel
will be used often in the following.
Notice that
![]() $W^\circ(\!\cdot\!)$
is a stationary process, and its integral
$W^\circ(\!\cdot\!)$
is a stationary process, and its integral
![]() $ W^*(\!\cdot\!)$
is a process with stationary increments.
$ W^*(\!\cdot\!)$
is a process with stationary increments.
1.2. Limit theorems for the workload
The main object of theoretical interest is the behavior of the integral workload as a process (function of time) observed on long time intervals.
In order to obtain a meaningful limit, we must scale (contract) the time, center the workload process, and divide it by an appropriate scalar factor.
Centering and scaling by an appropriate factor b leads to a normalized integral workload process
![]() $Z_a(t)\;:\!=\;({W^*(at)-{\mathbb E}\,R\cdot {\mathbb E}\,U\cdot a \lambda t})/{b}$
,
$Z_a(t)\;:\!=\;({W^*(at)-{\mathbb E}\,R\cdot {\mathbb E}\,U\cdot a \lambda t})/{b}$
,
![]() $b=b(a,\lambda)$
.
$b=b(a,\lambda)$
.
In order to obtain a limit theorem, we usually assume that either the variables R and U have finite variance, or their distributions have regular tails. More precisely, either
or
![]() ${\mathbb E}U^2< \infty$
. In the latter case we formally set
${\mathbb E}U^2< \infty$
. In the latter case we formally set
![]() $\gamma\;:\!=\;2$
.
$\gamma\;:\!=\;2$
.
Analogously, either
or
![]() ${\mathbb E}R^2< \infty$
. In the latter case we formally set
${\mathbb E}R^2< \infty$
. In the latter case we formally set
![]() $\delta\;:\!=\;2$
.
$\delta\;:\!=\;2$
.
Notice that in all these cases
![]() ${\mathbb E}\,R<\infty$
,
${\mathbb E}\,R<\infty$
,
![]() ${\mathbb E}\,U<\infty$
, and the workload processes are correctly defined.
${\mathbb E}\,U<\infty$
, and the workload processes are correctly defined.
The behavior of the service system crucially depends on the parameters
![]() $\gamma, \delta\in (1,2]$
.
$\gamma, \delta\in (1,2]$
.
It is remarkable that a simple tuning of the three parameters
![]() $\lambda$
,
$\lambda$
,
![]() $\gamma$
, and
$\gamma$
, and
![]() $\delta$
may lead to different limiting processes for
$\delta$
may lead to different limiting processes for
![]() $Z_a$
; namely, we can obtain
$Z_a$
; namely, we can obtain
Wiener process;
fractional Brownian motion with index
 $H\in(1/2,1)$
;
$H\in(1/2,1)$
;centered Lévy stable process with positive spectrum;
stable Telecom process;
Poisson Telecom process.
While the first three processes present a core of the classical theory of stochastic processes, the Telecom processes remain almost unstudied. In this article we focus on some key properties of the Poisson Telecom process.
For the full panorama of related limit theorems we refer to [Reference Lifshits11, Chapter 3], and recall here only one result concerning the Poisson Telecom process (cf. [Reference Lifshits11, Theorem 13.16]) related to the case of critical intensity,
![]() ${\lambda}/{a^{\gamma-1}}\to L$
,
${\lambda}/{a^{\gamma-1}}\to L$
,
![]() $0<L<\infty$
.
$0<L<\infty$
.
Theorem 1. Assume that conditions (2) and (3) hold with some
![]() $1<\gamma<\delta\le 2$
. Let
$1<\gamma<\delta\le 2$
. Let
![]() $a,\lambda\to\infty$
so that the critical intensity condition holds. Let
$a,\lambda\to\infty$
so that the critical intensity condition holds. Let
![]() $Q\;:\!=\;L {c_{\scriptscriptstyle U}} \gamma$
. Then, with scaling
$Q\;:\!=\;L {c_{\scriptscriptstyle U}} \gamma$
. Then, with scaling
![]() $b\;:\!=\;a$
the finite-dimensional distributions of the process
$b\;:\!=\;a$
the finite-dimensional distributions of the process
![]() $Z_a$
converge to those of the Poisson Telecom process
$Z_a$
converge to those of the Poisson Telecom process
![]() $Y_{Q,\gamma}$
admitting an integral representation
$Y_{Q,\gamma}$
admitting an integral representation
![]() $Y_{Q,\gamma}(t) = \int_\mathcal R r \ell_t(s,u) \, \bar N_{Q,\gamma}({\textrm{d}} s,{\textrm{d}} u,{\textrm{d}} r)$
. Here,
$Y_{Q,\gamma}(t) = \int_\mathcal R r \ell_t(s,u) \, \bar N_{Q,\gamma}({\textrm{d}} s,{\textrm{d}} u,{\textrm{d}} r)$
. Here,
![]() $\ell_{t}(s,u)$
is the kernel defined in (1), and
$\ell_{t}(s,u)$
is the kernel defined in (1), and
![]() $\bar N_{Q,\gamma}$
is a centered Poisson random measure of intensity
$\bar N_{Q,\gamma}$
is a centered Poisson random measure of intensity
![]() $Q\mu_{\gamma}$
, where
$Q\mu_{\gamma}$
, where
Poisson Telecom processes were introduced in [Reference Gaigalas and Kaj3] and placed into a more general picture in [Reference Kaj and Taqqu9]. For further studies on this subject we refer to [Reference Cohen and Taqqu1, Reference Gaigalas4]. In accordance with its role in the limit theorem, the process
![]() $(Y_{Q,\gamma}(t))_{t\ge 0}$
has stationary increments. It is, however, not self-similar like other limiting processes in the same model, such as Wiener processes, fractional Brownian motion, or strictly stable Lévy processes.
$(Y_{Q,\gamma}(t))_{t\ge 0}$
has stationary increments. It is, however, not self-similar like other limiting processes in the same model, such as Wiener processes, fractional Brownian motion, or strictly stable Lévy processes.
It is well known that the process
![]() $Y_{Q,\gamma}$
is correctly defined if
$Y_{Q,\gamma}$
is correctly defined if
![]() ${\mathbb E} (R^\gamma)<\infty$
. In the rest of the paper we make only this assumption on R and do not assume any tail regularity of R like the one required in (3). The only notable exception is the ultralarge-deviation case (Theorem 5) where the tail regularity appears to be essential.
${\mathbb E} (R^\gamma)<\infty$
. In the rest of the paper we make only this assumption on R and do not assume any tail regularity of R like the one required in (3). The only notable exception is the ultralarge-deviation case (Theorem 5) where the tail regularity appears to be essential.
2. Main results
2.1. A limit theorem for Telecom process
At large time scales the Poisson Telecom process essentially behaves as a
![]() $\gamma$
-stable Lévy process. This fact is basically known, but we present it here for completeness of exposition. The analogy with a stable law will also guide us (to some extent and within a certain range) in the subsequent studies of large-deviation probabilities.
$\gamma$
-stable Lévy process. This fact is basically known, but we present it here for completeness of exposition. The analogy with a stable law will also guide us (to some extent and within a certain range) in the subsequent studies of large-deviation probabilities.
Proposition 1. We have a weak convergence
where
![]() $\mathcal S_{Q,\gamma}$
is a centered strictly
$\mathcal S_{Q,\gamma}$
is a centered strictly
![]() $\gamma$
-stable random variable with positive spectrum, i.e.
$\gamma$
-stable random variable with positive spectrum, i.e.
2.2. Large deviations
According to Proposition 1, the large-deviation probabilities are
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t)$
as
${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t)$
as
![]() $y_t \gg t^{1/\gamma}$
. Their behavior may be different in different zones of
$y_t \gg t^{1/\gamma}$
. Their behavior may be different in different zones of
![]() $y_t$
and may depend on the distribution of R. Actually, three large-deviation zones emerge naturally:
$y_t$
and may depend on the distribution of R. Actually, three large-deviation zones emerge naturally:
Moderate large deviations:
 $t^{1/\gamma}\ll y_t \ll t$
. This case is completely explored in Section 2.2.1. The large-deviation probabilities behave exactly as those of the limiting stable process from Proposition 1.
$t^{1/\gamma}\ll y_t \ll t$
. This case is completely explored in Section 2.2.1. The large-deviation probabilities behave exactly as those of the limiting stable process from Proposition 1.Intermediate large deviations:
 $y_t = \kappa t$
. This case is explored in Section 2.2.2. The decay order of the large-deviation probabilities is still the same as for the limiting stable process but the corresponding constants are different. The study is quite involved, especially due to the tricky dependence of these new emerging constants on the distribution of R.
$y_t = \kappa t$
. This case is explored in Section 2.2.2. The decay order of the large-deviation probabilities is still the same as for the limiting stable process but the corresponding constants are different. The study is quite involved, especially due to the tricky dependence of these new emerging constants on the distribution of R.Ultralarge deviations:
 $y_t \gg t $
. This case is partially considered in Section 2.2.3. Here, the large-deviation probabilities are determined by the tail probabilities of the underlying random variable R. Our result is limited by one of the most natural cases, regular behavior of the tails. Solving the case of light tails in sufficient generality remains a challenging problem.
$y_t \gg t $
. This case is partially considered in Section 2.2.3. Here, the large-deviation probabilities are determined by the tail probabilities of the underlying random variable R. Our result is limited by one of the most natural cases, regular behavior of the tails. Solving the case of light tails in sufficient generality remains a challenging problem.
We present specific results in the following subsections.
2.2.1. Moderate large deviations
Theorem 2. Let
![]() $y_t$
be such that
$y_t$
be such that
![]() $t^{1/\gamma}\ll y_t \ll t$
. Then
$t^{1/\gamma}\ll y_t \ll t$
. Then
where
![]() $D \;:\!=\; {Q {\mathbb E}(R^\gamma)}/{\gamma}$
.
$D \;:\!=\; {Q {\mathbb E}(R^\gamma)}/{\gamma}$
.
This result should be compared with the limit theorem (4) because for the levels
![]() $\rho_t$
satisfying
$\rho_t$
satisfying
![]() $1\ll \rho_t \ll t^{(\gamma-1)/\gamma}$
, (5) yields
$1\ll \rho_t \ll t^{(\gamma-1)/\gamma}$
, (5) yields
 \begin{align*} {\mathbb P} \big( ({\mathbb E}(R^\gamma)t)^{-1/\gamma} Y_{Q,\gamma}(t)\ge \rho_t\big) & = {\mathbb P}\big( Y_{Q,\gamma}(t)\ge ({\mathbb E}(R^\gamma)t)^{1/\gamma} \rho_t\big) \\[5pt] & \sim D t ({\mathbb E}(R^\gamma)t)^{-1} \rho_t^{-\gamma} = \frac {Q}{\gamma}\ \rho_t^{-\gamma} \sim {\mathbb P}(\mathcal S_{Q,\gamma}\ge \rho_t) . \end{align*}
\begin{align*} {\mathbb P} \big( ({\mathbb E}(R^\gamma)t)^{-1/\gamma} Y_{Q,\gamma}(t)\ge \rho_t\big) & = {\mathbb P}\big( Y_{Q,\gamma}(t)\ge ({\mathbb E}(R^\gamma)t)^{1/\gamma} \rho_t\big) \\[5pt] & \sim D t ({\mathbb E}(R^\gamma)t)^{-1} \rho_t^{-\gamma} = \frac {Q}{\gamma}\ \rho_t^{-\gamma} \sim {\mathbb P}(\mathcal S_{Q,\gamma}\ge \rho_t) . \end{align*}
In other words, the moderate large-deviation probabilities are equivalent to those of the limiting distribution.
Using the terminology of the background service system, moderate deviation is attained by a unique heavy service process. We will stress this fact later in the proof.
2.2.2. Intermediate large deviations
The following result describes the situation on the upper boundary of the moderate deviations zone.
Theorem 3. Let
![]() $\kappa>0$
be such that
$\kappa>0$
be such that
![]() ${\mathbb P}(R\ge \kappa)>0$
and
${\mathbb P}(R\ge \kappa)>0$
and
Let
![]() $y_t\;:\!=\;\kappa t$
. Then
$y_t\;:\!=\;\kappa t$
. Then
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) = Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
as
${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) = Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
as
![]() $t\to\infty$
, where
$t\to\infty$
, where
Remark 1. There is a certain continuity between the asymptotic expressions in the zones of moderate and intermediate large deviations, as in the intermediate case we let
![]() $\kappa\to 0$
. Indeed, by plugging formally
$\kappa\to 0$
. Indeed, by plugging formally
![]() $y_t\;:\!=\;\kappa t$
into (5) we obtain the asymptotics
$y_t\;:\!=\;\kappa t$
into (5) we obtain the asymptotics
![]() ${Q {\mathbb E}(R^\gamma)}{\gamma}^{-1} \kappa^{-\gamma} t^{-(\gamma-1)}$
, while the first term in the definition of
${Q {\mathbb E}(R^\gamma)}{\gamma}^{-1} \kappa^{-\gamma} t^{-(\gamma-1)}$
, while the first term in the definition of
![]() $D_\textrm{I}^{(1)}(\kappa)$
taken alone provides almost the same asymptotics,
$D_\textrm{I}^{(1)}(\kappa)$
taken alone provides almost the same asymptotics,
![]() ${Q {\mathbb E}\big(R^\gamma{ {\mathbf 1}_{ \{{R\ge \kappa} \}}}\big)}{\gamma}^{-1} \kappa^{-\gamma} t^{-(\gamma-1)}$
, given that
${Q {\mathbb E}\big(R^\gamma{ {\mathbf 1}_{ \{{R\ge \kappa} \}}}\big)}{\gamma}^{-1} \kappa^{-\gamma} t^{-(\gamma-1)}$
, given that
![]() ${\mathbb E}\big(R^\gamma { {\mathbf 1}_{ \{{R\ge \kappa} \}}}\big)$
tends to
${\mathbb E}\big(R^\gamma { {\mathbf 1}_{ \{{R\ge \kappa} \}}}\big)$
tends to
![]() ${\mathbb E}(R^\gamma)$
as
${\mathbb E}(R^\gamma)$
as
![]() $\kappa\to 0$
. Moreover, when
$\kappa\to 0$
. Moreover, when
![]() $\kappa$
goes to zero, the second term in the definition of
$\kappa$
goes to zero, the second term in the definition of
![]() $D_\textrm{I}^{(1)}(\kappa)$
is negligible with respect to the first one because it contains an extra degree of
$D_\textrm{I}^{(1)}(\kappa)$
is negligible with respect to the first one because it contains an extra degree of
![]() $\kappa$
.
$\kappa$
.
Remark 2. If (6) does not hold, the decay order of large deviations will be the same but the expression for the corresponding constant becomes more involved and less explicit.
The attentive reader will notice that Theorem 3 does not work for large
![]() $\kappa$
if the distribution of R is compactly supported. Indeed, in this case the large-deviation asymptotics will be different, as the next result shows. In terms of the service system, it handles the case when the large deviation can be attained by accumulation of n heavy service processes but cannot be attained by
$\kappa$
if the distribution of R is compactly supported. Indeed, in this case the large-deviation asymptotics will be different, as the next result shows. In terms of the service system, it handles the case when the large deviation can be attained by accumulation of n heavy service processes but cannot be attained by
![]() $(n-1)$
such processes.
$(n-1)$
such processes.
Theorem 4. Let
![]() $\kappa>0$
. Assume that there is a positive integer n such that
$\kappa>0$
. Assume that there is a positive integer n such that
![]() ${\mathbb P}(R\ge {\kappa}/{n})>0$
but
${\mathbb P}(R\ge {\kappa}/{n})>0$
but
Assume that
where
![]() $R_1,\dots, R_n$
are independent copies of R.
$R_1,\dots, R_n$
are independent copies of R.
Let
![]() $y_t\;:\!=\;\kappa t$
. Then
$y_t\;:\!=\;\kappa t$
. Then
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) = Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
as
${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) = Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
as
![]() $t\to\infty$
, where
$t\to\infty$
, where
![]() $D^{(n)}_\textrm{I}(\kappa)$
is some finite positive constant depending on n,
$D^{(n)}_\textrm{I}(\kappa)$
is some finite positive constant depending on n,
![]() $\kappa$
, and on the law of R.
$\kappa$
, and on the law of R.
Remark 3. The explicit form of
![]() $D^{(n)}_\textrm{I}(\kappa)$
is given in (31).
$D^{(n)}_\textrm{I}(\kappa)$
is given in (31).
Remark 4. Theorem 4 does not cover the critical case
![]() $\zeta=1$
, where we have
$\zeta=1$
, where we have
![]() ${\mathbb P}(R\ge {\kappa}/({n-1}))=0$
but
${\mathbb P}(R\ge {\kappa}/({n-1}))=0$
but
![]() ${\mathbb P}(R\ge {\kappa}/({n-1})-\varepsilon)>0$
for all
${\mathbb P}(R\ge {\kappa}/({n-1})-\varepsilon)>0$
for all
![]() $\varepsilon>0$
. In this case, the assertion of the theorem may not hold because the large-deviation probability behavior depends on that of the upper tail,
$\varepsilon>0$
. In this case, the assertion of the theorem may not hold because the large-deviation probability behavior depends on that of the upper tail,
![]() ${\mathbb P}(R\in [{\kappa}/({n-1})-\varepsilon,{\kappa}/({n-1})))$
, as
${\mathbb P}(R\in [{\kappa}/({n-1})-\varepsilon,{\kappa}/({n-1})))$
, as
![]() $\varepsilon\to 0$
.
$\varepsilon\to 0$
.
2.2.3. Ultralarge deviations
Theorem 5. Let
![]() $y_t \gg t$
. Assume that the tail probability function
$y_t \gg t$
. Assume that the tail probability function
![]() ${\bar F_R}(r)\;:\!=\;{\mathbb P}(R\ge r)$
is regularly varying of negative order
${\bar F_R}(r)\;:\!=\;{\mathbb P}(R\ge r)$
is regularly varying of negative order
![]() $-m$
, where
$-m$
, where
![]() $m>\gamma$
. Then
$m>\gamma$
. Then
as
![]() $t\to\infty$
, where
$t\to\infty$
, where
As in Theorem 2, the workload’s large deviation is attained by a unique long and heavy service process.
We stress that the parameter m in Theorem 5 is allowed to be arbitrarily large. In particular, the case
![]() $m>2$
corresponds to the notation
$m>2$
corresponds to the notation
![]() $\delta=2$
used in the introduction. Therefore, we are not allowed to identify m with
$\delta=2$
used in the introduction. Therefore, we are not allowed to identify m with
![]() $\delta$
.
$\delta$
.
On the other hand, considering
![]() $m< \gamma$
is meaningless because for such a case our Telecom process
$m< \gamma$
is meaningless because for such a case our Telecom process
![]() $Y_{Q,\gamma}$
is simply not correctly defined.
$Y_{Q,\gamma}$
is simply not correctly defined.
2.3. Concluding remark
The challenging case of light tails of the distribution of R not covered by Theorem 5 remains beyond the scope of this article. Unlike all our results, here the workload’s large deviation may be achieved through many overlapping heavy service processes.
Consider a ‘toy’, but not completely trivial, example of deterministic R. Let
![]() ${\mathbb P}(R=1)=1$
. Then the contribution of any one service process is bounded by t. Therefore, in order to reach an ultralarge deviation level
${\mathbb P}(R=1)=1$
. Then the contribution of any one service process is bounded by t. Therefore, in order to reach an ultralarge deviation level
![]() $y_t\gg t$
we essentially need
$y_t\gg t$
we essentially need
![]() $y_t/t \to \infty$
long service processes of maximal length order t. By quantifying this idea, we get an exponential probability decay,
$y_t/t \to \infty$
long service processes of maximal length order t. By quantifying this idea, we get an exponential probability decay,
which is very different from the results of this article both in its form and in its nature.
We expect that for a sufficiently large class of distributions with light tails the results in the spirit of the classical large-deviation theory [Reference Dembo and Zeitouni2] might be relevant. This could be a subject of subsequent work.
3. Proofs
3.1. Preliminaries
Let us introduce two auxiliary intensity measures that play a central role in the whole paper. The first one corresponds to the kernel
![]() $\ell_t$
, namely
$\ell_t$
, namely
Recall that
![]() $\ell_t$
denotes the time length of a service process restricted to the interval [0, t]. These lengths form a Poisson random point process (or Poisson random measure), and
$\ell_t$
denotes the time length of a service process restricted to the interval [0, t]. These lengths form a Poisson random point process (or Poisson random measure), and
![]() $\mu^{(\ell)}_t$
is the corresponding intensity (or mean measure).
$\mu^{(\ell)}_t$
is the corresponding intensity (or mean measure).
The second measure is the ‘distribution’ of the product
![]() $r\ell_t(s,u)$
,
$r\ell_t(s,u)$
,
 \begin{align*} \mu^{(\ell,r)}_t (A) & \;:\!=\; \int_{{\mathbb R}_+} \int_{{\mathbb R}_+} { {\mathbf 1}_{ \{{ r \ell \in A} \}}} \, \mu^{(\ell)}_t({\textrm{d}}\ell) \, F_R({\textrm{d}} r) \\[5pt] & = \mu_\gamma\{(s,u,r)\colon r \ell_t(s,u)\in A\}, \qquad A\in\mathcal B({\mathbb R}_+).\end{align*}
\begin{align*} \mu^{(\ell,r)}_t (A) & \;:\!=\; \int_{{\mathbb R}_+} \int_{{\mathbb R}_+} { {\mathbf 1}_{ \{{ r \ell \in A} \}}} \, \mu^{(\ell)}_t({\textrm{d}}\ell) \, F_R({\textrm{d}} r) \\[5pt] & = \mu_\gamma\{(s,u,r)\colon r \ell_t(s,u)\in A\}, \qquad A\in\mathcal B({\mathbb R}_+).\end{align*}
Here, the product
![]() $r\ell_t$
represents the contribution of a service process to the integral workload of the system on the time interval [0, t]. Again, these contributions form a Poisson random point process, and
$r\ell_t$
represents the contribution of a service process to the integral workload of the system on the time interval [0, t]. Again, these contributions form a Poisson random point process, and
![]() $ \mu^{(\ell,r)}_t$
is the corresponding intensity.
$ \mu^{(\ell,r)}_t$
is the corresponding intensity.
Notice that the total mass of both measures is infinite due to the presence of infinitely many very short service processes.
A simple variable change
![]() $v=r\ell_t(s,u)$
in the definition of
$v=r\ell_t(s,u)$
in the definition of
![]() $Y_{Q,\gamma}(t)$
yields
$Y_{Q,\gamma}(t)$
yields
where
![]() ${\widetilde N}_{Q,\gamma}$
is a centered Poisson measure with intensity
${\widetilde N}_{Q,\gamma}$
is a centered Poisson measure with intensity
![]() $Q\mu^{(\ell,r)}_t$
. Therefore, the properties of
$Q\mu^{(\ell,r)}_t$
. Therefore, the properties of
![]() $\mu^{(\ell,r)}_t$
determine those of
$\mu^{(\ell,r)}_t$
determine those of
![]() $Y_{Q,\gamma}(t)$
.
$Y_{Q,\gamma}(t)$
.
As a first step, we give an explicit formula for the intermediate measure
![]() $\mu^{(\ell)}_t$
. First, by definition, we have
$\mu^{(\ell)}_t$
. First, by definition, we have
![]() $ \mu^{(\ell)}_t(t,\infty) =0$
. Next, let us fix an
$ \mu^{(\ell)}_t(t,\infty) =0$
. Next, let us fix an
![]() $\ell_0\in (0,t]$
and find
$\ell_0\in (0,t]$
and find
![]() $\mu^{(\ell)}_t[\ell_0,t]$
. In fact,
$\mu^{(\ell)}_t[\ell_0,t]$
. In fact,
![]() $\ell_t(s,u)\ge \ell_0$
if and only if
$\ell_t(s,u)\ge \ell_0$
if and only if
![]() $u\ge \ell_0$
and
$u\ge \ell_0$
and
![]() $s\in[\ell_0-u,t-\ell_0]$
. Therefore,
$s\in[\ell_0-u,t-\ell_0]$
. Therefore,
It follows that the measure
![]() $\mu^{(\ell)}_t$
has an atom with weight
$\mu^{(\ell)}_t$
has an atom with weight
![]() ${t^{-(\gamma-1)}}/{(\gamma-1)\gamma}$
at the right boundary point t, and a density
${t^{-(\gamma-1)}}/{(\gamma-1)\gamma}$
at the right boundary point t, and a density
For each
![]() $\ell_0>0$
, (10) also yields the bound
$\ell_0>0$
, (10) also yields the bound
Finally, consider the asymptotic behavior of
Assume that
![]() $y_t\to\infty$
but
$y_t\to\infty$
but
![]() $y_t/t\to 0$
. Then it follows from (10) that, for every fixed r,
$y_t/t\to 0$
. Then it follows from (10) that, for every fixed r,
By using (11), we also have an integrable majorant with respect to the law
![]() $F_R$
:
$F_R$
:
By integrating this estimate in (12) we obtain
Furthermore, by Lebesgue’s dominated convergence theorem, (12) and (13) yield
3.2. Proof of Proposition 1
Proof. Consider the integral representation (9). According to a general criterion of the weak convergence of Poisson integrals to a stable law [Reference Lifshits11, Corollary 8.5], it is enough to check that, for each fixed
![]() $\rho>0$
,
$\rho>0$
,
combined with the uniform bound
Indeed, by substituting
![]() $y_t\;:\!=\;\rho ( {\mathbb E}(R^\gamma) t)^{1/\gamma}$
in (15) we obtain (16), and by making the same substitution in (14) we obtain (17).
$y_t\;:\!=\;\rho ( {\mathbb E}(R^\gamma) t)^{1/\gamma}$
in (15) we obtain (16), and by making the same substitution in (14) we obtain (17).
3.3. A decomposition
Take some
![]() $v_0>0$
and split the integral representation (9) into three parts:
$v_0>0$
and split the integral representation (9) into three parts:
 \begin{align} Y_{Q,\gamma}(t) & = \int_{0}^{v_0} v \, {\widetilde N}_{Q,\gamma}({\textrm{d}} v) + \int_{v_0}^\infty v \, N_{Q,\gamma}({\textrm{d}} v) - Q \int_{v_0}^\infty v \, \mu^{(\ell,r)}_t({\textrm{d}} v) \nonumber \\[5pt] & \;:\!=\; Y^\circ(t) + Y^{\dagger}(t)-E_t,\end{align}
\begin{align} Y_{Q,\gamma}(t) & = \int_{0}^{v_0} v \, {\widetilde N}_{Q,\gamma}({\textrm{d}} v) + \int_{v_0}^\infty v \, N_{Q,\gamma}({\textrm{d}} v) - Q \int_{v_0}^\infty v \, \mu^{(\ell,r)}_t({\textrm{d}} v) \nonumber \\[5pt] & \;:\!=\; Y^\circ(t) + Y^{\dagger}(t)-E_t,\end{align}
where
![]() $N_{Q,\gamma}$
is the corresponding non-centered Poisson random measure and
$N_{Q,\gamma}$
is the corresponding non-centered Poisson random measure and
![]() $E_t$
is the centering deterministic function.
$E_t$
is the centering deterministic function.
The variance of
![]() $ Y^\circ(t)$
admits the upper bound
$ Y^\circ(t)$
admits the upper bound
Using (14) we get
where
Similarly, the centering term admits the bound
where
3.4. A lower bound for large deviations
We will give a lower bound for large-deviation probabilities
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t)$
with
${\mathbb P}( Y_{Q,\gamma}(t)\ge y_t)$
with
![]() $y_t \gg t^{1/\gamma}$
. Let
$y_t \gg t^{1/\gamma}$
. Let
![]() $h,\varepsilon$
be small positive numbers. Define
$h,\varepsilon$
be small positive numbers. Define
![]() $v_0\;:\!=\; hy_t$
and consider the corresponding decomposition (18).
$v_0\;:\!=\; hy_t$
and consider the corresponding decomposition (18).
First of all, notice that
![]() $E_t$
is negligible at the range
$E_t$
is negligible at the range
![]() $y_t$
because, by (20),
$y_t$
because, by (20),
![]() $E_t\le D_1 t (hy_t)^{1-\gamma} = D_1 h^{1-\gamma} (t^{-1/\gamma}y_t)^{-\gamma} y_t = o(y_t)$
. Therefore, we may, and do, assume t to be so large that
$E_t\le D_1 t (hy_t)^{1-\gamma} = D_1 h^{1-\gamma} (t^{-1/\gamma}y_t)^{-\gamma} y_t = o(y_t)$
. Therefore, we may, and do, assume t to be so large that
![]() $E_t\le \varepsilon y_t$
.
$E_t\le \varepsilon y_t$
.
Using (19), by Chebyshev’s inequality we have
It is also useful to notice that, for each fixed
![]() $\rho>0$
and all large t,
$\rho>0$
and all large t,
 \begin{align*} \mu^{(\ell,r)}_t[v_0,\infty) & = \mu^{(\ell,r)}_t[hy_t,\infty) = \mu^{(\ell,r)}_t[h (t^{-1/\gamma}y_t) t^{1/\gamma},\infty) \\[5pt] & \le \mu^{(\ell,r)}_t[h \rho t^{1/\gamma},\infty) \le \frac{{\mathbb E}(R^\gamma)}{\gamma(\gamma-1)} (h \rho)^{-\gamma},\end{align*}
\begin{align*} \mu^{(\ell,r)}_t[v_0,\infty) & = \mu^{(\ell,r)}_t[hy_t,\infty) = \mu^{(\ell,r)}_t[h (t^{-1/\gamma}y_t) t^{1/\gamma},\infty) \\[5pt] & \le \mu^{(\ell,r)}_t[h \rho t^{1/\gamma},\infty) \le \frac{{\mathbb E}(R^\gamma)}{\gamma(\gamma-1)} (h \rho)^{-\gamma},\end{align*}
where we used (14) at the last step. Letting
![]() $\rho\to\infty$
we get
$\rho\to\infty$
we get
![]() $\mu^{(\ell,r)}_t[v_0,\infty) \to 0$
as
$\mu^{(\ell,r)}_t[v_0,\infty) \to 0$
as
![]() $t\to\infty$
.
$t\to\infty$
.
Using the basic properties of Poisson random measure, we may proceed now with the required lower bound as follows:
 \begin{align*} {\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t, Y^{\dagger}(t)\ge (1+2\varepsilon)y_t) \\[5pt] & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t) {\mathbb P}( Y^{\dagger}(t)\ge (1+2\varepsilon)y_t;\; N_{Q,\gamma}[v_0,\infty)=1) \\[5pt] & = {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t) \exp\{-Q\mu^{(\ell,r)}_t[v_0,\infty)\} Q \mu^{(\ell,r)}_t[(1+2\varepsilon)y_t,\infty).\end{align*}
\begin{align*} {\mathbb P}( Y_{Q,\gamma}(t)\ge y_t) & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t, Y^{\dagger}(t)\ge (1+2\varepsilon)y_t) \\[5pt] & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t) {\mathbb P}( Y^{\dagger}(t)\ge (1+2\varepsilon)y_t;\; N_{Q,\gamma}[v_0,\infty)=1) \\[5pt] & = {\mathbb P}( |Y^\circ(t)|\le \varepsilon y_t) \exp\{-Q\mu^{(\ell,r)}_t[v_0,\infty)\} Q \mu^{(\ell,r)}_t[(1+2\varepsilon)y_t,\infty).\end{align*}
The idea behind this bound is to take a single service process providing a substantial large-deviation workload and to suppress other contributions.
As we have just seen, the first two factors tend to one, thus
3.5. An upper bound for large deviations
Starting again with the representation in (18), using
![]() $E_t\ge 0$
and (21) we have
$E_t\ge 0$
and (21) we have
 \begin{align} \nonumber {\mathbb P}( & Y_{Q,\gamma}(t) \ge y_t) \\[5pt] \nonumber & \le {\mathbb P}( Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(N_{Q,\gamma}[v_0,\infty)\ge 2) + {\mathbb P}( Y^{\dagger}(t)\ge (1-\varepsilon)y_t;\; N_{Q,\gamma}[v_0,\infty)=1) \\[5pt] \nonumber & = {\mathbb P}( Y^\circ(t) \ge \varepsilon y_t) + {\mathbb P}(N_{Q,\gamma}[v_0,\infty)\ge 2) + {\mathbb P}(N_{Q,\gamma}[(1-\varepsilon)y_t,\infty)=1) \\[5pt] & \le \frac{ D_2 t h^{2-\gamma}}{\varepsilon^2y_t^\gamma} + \frac 12 \big( Q\mu^{(\ell,r)}_t[v_0,\infty)\big)^2 +Q\mu^{(\ell,r)}_t[(1-\varepsilon)y_t,\infty).\end{align}
\begin{align} \nonumber {\mathbb P}( & Y_{Q,\gamma}(t) \ge y_t) \\[5pt] \nonumber & \le {\mathbb P}( Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(N_{Q,\gamma}[v_0,\infty)\ge 2) + {\mathbb P}( Y^{\dagger}(t)\ge (1-\varepsilon)y_t;\; N_{Q,\gamma}[v_0,\infty)=1) \\[5pt] \nonumber & = {\mathbb P}( Y^\circ(t) \ge \varepsilon y_t) + {\mathbb P}(N_{Q,\gamma}[v_0,\infty)\ge 2) + {\mathbb P}(N_{Q,\gamma}[(1-\varepsilon)y_t,\infty)=1) \\[5pt] & \le \frac{ D_2 t h^{2-\gamma}}{\varepsilon^2y_t^\gamma} + \frac 12 \big( Q\mu^{(\ell,r)}_t[v_0,\infty)\big)^2 +Q\mu^{(\ell,r)}_t[(1-\varepsilon)y_t,\infty).\end{align}
Here, the last term is the main one. Recall that almost the same expression also shows up in the lower bound.
3.6. Proof of Theorem 2
Proof. Recall that, according to (15), in the zone under consideration,
![]() $t^{1/\gamma}\ll y_t\ll t$
, it is true that
$t^{1/\gamma}\ll y_t\ll t$
, it is true that
and we have similar representations with
![]() $y_t$
replaced by either
$y_t$
replaced by either
![]() $(1+2\varepsilon)y_t$
,
$(1+2\varepsilon)y_t$
,
![]() $(1-\varepsilon)y_t$
, or
$(1-\varepsilon)y_t$
, or
![]() $v_0=hy_t$
.
$v_0=hy_t$
.
In view of (24), the lower estimate (22) yields
while the upper estimate (23) yields
because the second term in (23) has a lower order of magnitude.
First letting
![]() $h\to 0$
, then
$h\to 0$
, then
![]() $\varepsilon\to 0$
, we obtain
$\varepsilon\to 0$
, we obtain
as required.
3.7. Proof of Theorem 3
Proof. The proof goes along the same lines as in the moderate-deviation case, except for the evaluation of
![]() $\mu^{(\ell,r)}_t[y_t,\infty)$
. Instead of (24), we have the following non-asymptotic exact formula. According to (10), for
$\mu^{(\ell,r)}_t[y_t,\infty)$
. Instead of (24), we have the following non-asymptotic exact formula. According to (10), for
![]() $y_t=\kappa t$
we have
$y_t=\kappa t$
we have
 \begin{align*} \mu^{(\ell,r)}_t[y_t,\infty) & = \int_0^\infty \mu^{(\ell)}_t\bigg[ \frac{y_t}{r}, \infty \bigg) F_R({\textrm{d}} r) \\[5pt] & = \int_\kappa^\infty \bigg( t \frac{(y_t/r)^{-\gamma}}{\gamma} + \frac{2-\gamma}{(\gamma-1)\gamma} (y_t/r)^{1-\gamma} \bigg) F_R({\textrm{d}} r) \\[5pt] & = \int_\kappa^\infty \bigg( \frac{\kappa^{-\gamma}}{\gamma} r^{\gamma} + \frac{(2-\gamma)\kappa^{1-\gamma} }{(\gamma-1)\gamma} r^{\gamma-1} \bigg) F_R({\textrm{d}} r) t^{-(\gamma-1)} \\[5pt] & = \bigg( \frac{\kappa^{-\gamma}}{\gamma} {\mathbb E}\big(R^{\gamma}{ {\mathbf 1}_{ \{{R\ge\kappa} \}}}\big) + \frac{(2-\gamma)\kappa^{1-\gamma} }{(\gamma-1)\gamma} {\mathbb E}\big(R^{\gamma-1}{ {\mathbf 1}_{ \{{R\ge\kappa} \}}}\big) \bigg) t^{-(\gamma-1)} \\[5pt] & = D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)}.\end{align*}
\begin{align*} \mu^{(\ell,r)}_t[y_t,\infty) & = \int_0^\infty \mu^{(\ell)}_t\bigg[ \frac{y_t}{r}, \infty \bigg) F_R({\textrm{d}} r) \\[5pt] & = \int_\kappa^\infty \bigg( t \frac{(y_t/r)^{-\gamma}}{\gamma} + \frac{2-\gamma}{(\gamma-1)\gamma} (y_t/r)^{1-\gamma} \bigg) F_R({\textrm{d}} r) \\[5pt] & = \int_\kappa^\infty \bigg( \frac{\kappa^{-\gamma}}{\gamma} r^{\gamma} + \frac{(2-\gamma)\kappa^{1-\gamma} }{(\gamma-1)\gamma} r^{\gamma-1} \bigg) F_R({\textrm{d}} r) t^{-(\gamma-1)} \\[5pt] & = \bigg( \frac{\kappa^{-\gamma}}{\gamma} {\mathbb E}\big(R^{\gamma}{ {\mathbf 1}_{ \{{R\ge\kappa} \}}}\big) + \frac{(2-\gamma)\kappa^{1-\gamma} }{(\gamma-1)\gamma} {\mathbb E}\big(R^{\gamma-1}{ {\mathbf 1}_{ \{{R\ge\kappa} \}}}\big) \bigg) t^{-(\gamma-1)} \\[5pt] & = D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)}.\end{align*}
The latter constant is positive due to the assumption
![]() ${\mathbb P}(R\ge \kappa)>0$
.
${\mathbb P}(R\ge \kappa)>0$
.
For the lower bound, the estimate in (22) yields
Letting
![]() $\varepsilon\searrow 0$
and using (6), we have
$\varepsilon\searrow 0$
and using (6), we have
Therefore,
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \ge Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
, as required.
${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \ge Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
, as required.
For the upper bound, the estimate in (23) with
![]() $y_t=\kappa t$
yields
$y_t=\kappa t$
yields
First letting
![]() $h\searrow 0$
, we get rid of the first term and obtain
$h\searrow 0$
, we get rid of the first term and obtain
Letting
![]() $\varepsilon\searrow 0$
, we have
$\varepsilon\searrow 0$
, we have
![]() $\lim_{\varepsilon\searrow 0} D^{(1)}_\textrm{I}((1-\varepsilon)\kappa)= D^{(1)}_\textrm{I}(\kappa)$
. Therefore,
$\lim_{\varepsilon\searrow 0} D^{(1)}_\textrm{I}((1-\varepsilon)\kappa)= D^{(1)}_\textrm{I}(\kappa)$
. Therefore,
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \le Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
, as required.
${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \le Q D^{(1)}_\textrm{I}(\kappa) t^{-(\gamma-1)} (1+o(1))$
, as required.
3.8. Proof of Theorem 4
In the setting of this theorem, the large-deviation probabilities decay faster with t than Chebyshev’s inequality (21) suggests. Therefore, we need the finer estimate for
![]() $Y^\circ(t)$
given in the following lemma.
$Y^\circ(t)$
given in the following lemma.
Lemma 1. For every
![]() $M,\varepsilon > 0$
there exist
$M,\varepsilon > 0$
there exist
![]() $h>0$
and
$h>0$
and
![]() $C=C(h,\varepsilon)>0$
such that, for all
$C=C(h,\varepsilon)>0$
such that, for all
![]() $t>0$
,
$t>0$
,
![]() ${\mathbb P}(Y^\circ(t)\ge \varepsilon t) \le C t^{-(\gamma-1)M}$
, where
${\mathbb P}(Y^\circ(t)\ge \varepsilon t) \le C t^{-(\gamma-1)M}$
, where
![]() $Y^\circ(t)$
is defined by (18) with the splitting point
$Y^\circ(t)$
is defined by (18) with the splitting point
![]() $v_0\;:\!=\;ht$
.
$v_0\;:\!=\;ht$
.
Proof. We start with some calculations valid for arbitrary
![]() $v_0$
. We have the following formula for the exponential moment of the centered Poisson integral:
$v_0$
. We have the following formula for the exponential moment of the centered Poisson integral:
We can split the integration domain here into two parts:
![]() $[0,v_0/2]$
and
$[0,v_0/2]$
and
![]() $(v_0/2,v_0]$
. For the second one we have
$(v_0/2,v_0]$
. For the second one we have
At the last step we used (14).
For the first zone, by using the inequality
![]() ${\textrm{e}}^x - 1 - x \le x^2 {\textrm{e}}^x$
and (14) we have
${\textrm{e}}^x - 1 - x \le x^2 {\textrm{e}}^x$
and (14) we have
 \begin{align*} \int_0^{\frac{v_0}{2}} ({\textrm{e}}^{\lambda v} - 1 - \lambda v) \mu^{(\ell,r)}_t({\textrm{d}} v) & \le \int_0^{\frac{v_0}{2}} \lambda^2 v^2 {\textrm{e}}^{\lambda v} \mu^{(\ell,r)}_t({\textrm{d}} v) \\[5pt] & \le 2 {\textrm{e}}^{\lambda v_0/2} \lambda^2 \int_0^{\frac{v_0}{2}} v \mu^{(\ell,r)}_t[v,v_0/2] \, {\textrm{d}} v \\[5pt] & \le \frac{2 {\mathbb E} (R^\gamma)}{\gamma(\gamma-1)} {\textrm{e}}^{\lambda v_0/2} \lambda^2 t \int_0^{\frac{v_0}{2}} v^{1-\gamma} \, {\textrm{d}} v \\[5pt] & = D_4 {\textrm{e}}^{\lambda v_0/2} \lambda^2 t v_0^{2-\gamma}, \qquad D_4 \;:\!=\; \frac{2^{\gamma-1} {\mathbb E} (R^\gamma)}{\gamma(\gamma-1)(2-\gamma)}.\end{align*}
\begin{align*} \int_0^{\frac{v_0}{2}} ({\textrm{e}}^{\lambda v} - 1 - \lambda v) \mu^{(\ell,r)}_t({\textrm{d}} v) & \le \int_0^{\frac{v_0}{2}} \lambda^2 v^2 {\textrm{e}}^{\lambda v} \mu^{(\ell,r)}_t({\textrm{d}} v) \\[5pt] & \le 2 {\textrm{e}}^{\lambda v_0/2} \lambda^2 \int_0^{\frac{v_0}{2}} v \mu^{(\ell,r)}_t[v,v_0/2] \, {\textrm{d}} v \\[5pt] & \le \frac{2 {\mathbb E} (R^\gamma)}{\gamma(\gamma-1)} {\textrm{e}}^{\lambda v_0/2} \lambda^2 t \int_0^{\frac{v_0}{2}} v^{1-\gamma} \, {\textrm{d}} v \\[5pt] & = D_4 {\textrm{e}}^{\lambda v_0/2} \lambda^2 t v_0^{2-\gamma}, \qquad D_4 \;:\!=\; \frac{2^{\gamma-1} {\mathbb E} (R^\gamma)}{\gamma(\gamma-1)(2-\gamma)}.\end{align*}
Next, using the inequality
![]() ${\textrm{e}}^{\frac{x}{2}}x^2 \le 3 {\textrm{e}}^x$
, we have
${\textrm{e}}^{\frac{x}{2}}x^2 \le 3 {\textrm{e}}^x$
, we have
Summing (25) and (26), we obtain
![]() ${\mathbb E\,} \exp\!(\lambda Y^\circ(t)) \le \exp\{ \left( D_3+ 3 D_4\right) t v_0^{-\gamma} {\textrm{e}}^{\lambda v_0}\}\;:\!=\; \exp\{ A {\textrm{e}}^{\lambda v_0} \}$
, where
${\mathbb E\,} \exp\!(\lambda Y^\circ(t)) \le \exp\{ \left( D_3+ 3 D_4\right) t v_0^{-\gamma} {\textrm{e}}^{\lambda v_0}\}\;:\!=\; \exp\{ A {\textrm{e}}^{\lambda v_0} \}$
, where
![]() $A \;:\!=\; (D_3+3D_4)tv_0^{-\gamma}$
. For every real z, by the exponential Chebyshev inequality we have
$A \;:\!=\; (D_3+3D_4)tv_0^{-\gamma}$
. For every real z, by the exponential Chebyshev inequality we have
If
![]() $z>Av_0$
, the minimum on the right-hand side is attained at the point
$z>Av_0$
, the minimum on the right-hand side is attained at the point
![]() $\lambda = ({1}/{v_0}) \log\!({z}/{Av_0})$
. By plugging this value into (27) we obtain
$\lambda = ({1}/{v_0}) \log\!({z}/{Av_0})$
. By plugging this value into (27) we obtain
Letting
![]() $z\;:\!=\;\varepsilon t$
,
$z\;:\!=\;\varepsilon t$
,
![]() $v_0\;:\!=\;ht$
yields
$v_0\;:\!=\;ht$
yields
![]() ${\mathbb P}(Y^\circ(t)\ge \varepsilon t) \le C t^{-\frac{\varepsilon}{h}(\gamma-1)}$
, where C depends only on
${\mathbb P}(Y^\circ(t)\ge \varepsilon t) \le C t^{-\frac{\varepsilon}{h}(\gamma-1)}$
, where C depends only on
![]() $\varepsilon$
and h. Choosing
$\varepsilon$
and h. Choosing
![]() $h < \frac{\varepsilon}{M}$
, we get the result.
$h < \frac{\varepsilon}{M}$
, we get the result.
Now we can proceed to the proof of the theorem.
Proof of Theorem
4. We start with the upper bound. Let
![]() $\eta\;:\!=\;{(1-\zeta)\kappa}/({n-\zeta})$
. Since
$\eta\;:\!=\;{(1-\zeta)\kappa}/({n-\zeta})$
. Since
![]() $\zeta\in (0,1)$
, we have
$\zeta\in (0,1)$
, we have
![]() $\eta>0$
. It also follows from the definition that
$\eta>0$
. It also follows from the definition that
![]() ${\kappa}/({n-\zeta})=({\kappa-\eta})/({n-1})$
. Therefore, we may rewrite (7) as
${\kappa}/({n-\zeta})=({\kappa-\eta})/({n-1})$
. Therefore, we may rewrite (7) as
Let
![]() $\varepsilon\in(0,\eta)$
. We now use the decomposition in (18) with the splitting point
$\varepsilon\in(0,\eta)$
. We now use the decomposition in (18) with the splitting point
![]() $v_0=ht$
, where h is small number. More precisely, by using Lemma 1 with
$v_0=ht$
, where h is small number. More precisely, by using Lemma 1 with
![]() $M=n+1$
we find a small
$M=n+1$
we find a small
![]() $h>0$
such that
$h>0$
such that
Taking into account
![]() $E_t\ge 0$
, we get the bound
$E_t\ge 0$
, we get the bound
By (30), the first term is negligible compared with the decay order
![]() $ t^{-(\gamma-1)n}$
announced in the theorem. Let us write
$ t^{-(\gamma-1)n}$
announced in the theorem. Let us write
![]() $N_0\;:\!=\;N_{Q,\gamma}[v_0,\infty)$
, which is a Poissonian random variable with intensity
$N_0\;:\!=\;N_{Q,\gamma}[v_0,\infty)$
, which is a Poissonian random variable with intensity
![]() $\mu_0\;:\!=\;Q \mu^{(\ell,r)}_t[v_0,\infty)$
, and apply the following bound to the second term:
$\mu_0\;:\!=\;Q \mu^{(\ell,r)}_t[v_0,\infty)$
, and apply the following bound to the second term:
 \begin{align*} {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t\big) \le {\mathbb P}(N_0>n) & + {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t;\; N_0=n\big) \\[5pt] & + {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t, N_0\le n-1\big). \end{align*}
\begin{align*} {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t\big) \le {\mathbb P}(N_0>n) & + {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t;\; N_0=n\big) \\[5pt] & + {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t, N_0\le n-1\big). \end{align*}
For the first term, an elementary bound for the Poisson tail works, namely
 \[ {\mathbb P}(N_0>n) = {\textrm{e}}^{-\mu_0}\sum_{j=0}^\infty \frac{\mu_0^{n+1+j}}{(n+1+j)!} \le {\textrm{e}}^{-\mu_0} \frac{\mu_0^{n+1}}{(n+1)!} \sum_{j=0}^\infty \frac{\mu_0^{j}}{j!} \le \frac{\mu_0^{n+1}}{(n+1)!} , \]
\[ {\mathbb P}(N_0>n) = {\textrm{e}}^{-\mu_0}\sum_{j=0}^\infty \frac{\mu_0^{n+1+j}}{(n+1+j)!} \le {\textrm{e}}^{-\mu_0} \frac{\mu_0^{n+1}}{(n+1)!} \sum_{j=0}^\infty \frac{\mu_0^{j}}{j!} \le \frac{\mu_0^{n+1}}{(n+1)!} , \]
where we used that
![]() $(n+1+j)!\ge (n+1)! j!$
. Notice that by (14) with
$(n+1+j)!\ge (n+1)! j!$
. Notice that by (14) with
![]() $y_t\;:\!=\;v_0=ht$
we have
$y_t\;:\!=\;v_0=ht$
we have
and hence
![]() ${\mathbb P}(N_0>n) = O\big( t^{-(\gamma-1)(n+1)}\big)$
is negligible compared to the term
${\mathbb P}(N_0>n) = O\big( t^{-(\gamma-1)(n+1)}\big)$
is negligible compared to the term
![]() $t^{-(\gamma-1)n}$
in the theorem’s assertion.
$t^{-(\gamma-1)n}$
in the theorem’s assertion.
Further, by using (29) and the definition of the measure
![]() $\mu^{(\ell,r)}_t$
, we see that
$\mu^{(\ell,r)}_t$
, we see that
which implies
![]() ${\mathbb P}(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t, N_0\le n-1)=0$
, because here the Poissonian integral
${\mathbb P}(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t, N_0\le n-1)=0$
, because here the Poissonian integral
![]() $Y^{\dagger}(t)$
is a sum of not more than
$Y^{\dagger}(t)$
is a sum of not more than
![]() $n-1$
terms each being strictly smaller than
$n-1$
terms each being strictly smaller than
![]() ${(\kappa-\varepsilon)t}/({n-1})$
.
${(\kappa-\varepsilon)t}/({n-1})$
.
For
![]() $A \in \mathcal B ([v_0, \infty))$
, we write
$A \in \mathcal B ([v_0, \infty))$
, we write
![]() $N_A\;:\!=\;N_{Q,\gamma}(A)$
with intensity
$N_A\;:\!=\;N_{Q,\gamma}(A)$
with intensity
![]() $\mu_A \;:\!=\; Q \mu^{(\ell,r)}_t(A)$
and
$\mu_A \;:\!=\; Q \mu^{(\ell,r)}_t(A)$
and
![]() $\nu_t^{(l,r)}(A) \;:\!=\; {\mathbb P}(N_A = 1 \mid N_0 = 1)$
, which is a measure on
$\nu_t^{(l,r)}(A) \;:\!=\; {\mathbb P}(N_A = 1 \mid N_0 = 1)$
, which is a measure on
![]() $[v_0, \infty)$
. We therefore have
$[v_0, \infty)$
. We therefore have
![]() $\nu_t^{(l,r)}(A) = {\textrm{e}}^{-\mu_A} \mu_A \cdot {\textrm{e}}^{\mu_A - \mu_0} \cdot ({{\textrm{e}}^{\mu_0}}/{\mu_0}) = {\mu_A}/{\mu_0}$
.
$\nu_t^{(l,r)}(A) = {\textrm{e}}^{-\mu_A} \mu_A \cdot {\textrm{e}}^{\mu_A - \mu_0} \cdot ({{\textrm{e}}^{\mu_0}}/{\mu_0}) = {\mu_A}/{\mu_0}$
.
The remaining Poissonian integral with a fixed number of points admits the following representation:
 \begin{align*} {\mathbb P}(Y^{\dagger}&(t)\ge (\kappa-\varepsilon) t;\; N_0=n) \\[5pt] & = {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t \mid N_0=n\big) {\mathbb P}(N_0 = n) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{\mu_0^n}{n!} \int_{[v_0,\infty)^n} { {\mathbf 1}_{ \{{v_1+\cdots+v_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \nu_t^{(l,r)}({\textrm{d}} v_j) \\[5pt] & \le {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{{\mathbb R}_+^n} { {\mathbf 1}_{ \{{v_1+\cdots+v_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \mu^{(\ell,r)}_t({\textrm{d}} v_j) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{[0,t]^n}\int_{R_+^n} { {\mathbf 1}_{ \{{\ell_1 r_1+\cdots+\ell_n r_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \mu^{(\ell)}_t({\textrm{d}}\ell_j) \prod_{j=1}^n F_R({\textrm{d}} r_j) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa-\varepsilon) \prod_{j=1}^n \nu({\textrm{d}} s_j) t^{-(\gamma-1)n}, \\[5pt] & \;:\!=\; {\textrm{e}}^{-\mu_0} Q^n D_\textrm{I}^{(n)}(\kappa-\varepsilon) t^{-(\gamma-1)n}, \end{align*}
\begin{align*} {\mathbb P}(Y^{\dagger}&(t)\ge (\kappa-\varepsilon) t;\; N_0=n) \\[5pt] & = {\mathbb P}\big(Y^{\dagger}(t)\ge (\kappa-\varepsilon) t \mid N_0=n\big) {\mathbb P}(N_0 = n) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{\mu_0^n}{n!} \int_{[v_0,\infty)^n} { {\mathbf 1}_{ \{{v_1+\cdots+v_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \nu_t^{(l,r)}({\textrm{d}} v_j) \\[5pt] & \le {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{{\mathbb R}_+^n} { {\mathbf 1}_{ \{{v_1+\cdots+v_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \mu^{(\ell,r)}_t({\textrm{d}} v_j) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{[0,t]^n}\int_{R_+^n} { {\mathbf 1}_{ \{{\ell_1 r_1+\cdots+\ell_n r_n\ge (\kappa-\varepsilon)t} \}}} \prod_{j=1}^n \mu^{(\ell)}_t({\textrm{d}}\ell_j) \prod_{j=1}^n F_R({\textrm{d}} r_j) \\[5pt] & = {\textrm{e}}^{-\mu_0} \frac{Q^n}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa-\varepsilon) \prod_{j=1}^n \nu({\textrm{d}} s_j) t^{-(\gamma-1)n}, \\[5pt] & \;:\!=\; {\textrm{e}}^{-\mu_0} Q^n D_\textrm{I}^{(n)}(\kappa-\varepsilon) t^{-(\gamma-1)n}, \end{align*}
where
![]() $R_1, \ldots, R_n$
are independent and identically distributed variables with distribution
$R_1, \ldots, R_n$
are independent and identically distributed variables with distribution
![]() $F_R$
and, according to (10),
$F_R$
and, according to (10),
![]() $\nu$
is a measure on [0, 1] having the atom
$\nu$
is a measure on [0, 1] having the atom
![]() ${1}/({\gamma(\gamma-1)})$
at 1 and the density
${1}/({\gamma(\gamma-1)})$
at 1 and the density
Notice also that the constant
![]() $D^{(n)}_\textrm{I}(\kappa-\varepsilon)$
is finite although the measure
$D^{(n)}_\textrm{I}(\kappa-\varepsilon)$
is finite although the measure
![]() $\nu$
is infinite at each neighborhood of zero. The reason is that the probability we integrate vanishes if, for some i, we have
$\nu$
is infinite at each neighborhood of zero. The reason is that the probability we integrate vanishes if, for some i, we have
![]() $s_i < s_* \;:\!=\; {(n-1)(\eta-\varepsilon)}/({\kappa-\eta})$
where
$s_i < s_* \;:\!=\; {(n-1)(\eta-\varepsilon)}/({\kappa-\eta})$
where
![]() $\eta>0$
satisfies (29). Indeed, in this case we have
$\eta>0$
satisfies (29). Indeed, in this case we have
 \begin{align*} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa-\varepsilon) & \le {\mathbb P}\big((s_*+(n-1)) \max\nolimits_{1\le j\le n} R_j\ge \kappa-\varepsilon \big) \\[5pt] & \le n {\mathbb P}\bigg( R\ge \frac{\kappa-\varepsilon}{s_*+(n-1)}\bigg) = n {\mathbb P}\bigg( R\ge \frac{\kappa-\eta}{n-1}\bigg) = 0. \end{align*}
\begin{align*} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa-\varepsilon) & \le {\mathbb P}\big((s_*+(n-1)) \max\nolimits_{1\le j\le n} R_j\ge \kappa-\varepsilon \big) \\[5pt] & \le n {\mathbb P}\bigg( R\ge \frac{\kappa-\varepsilon}{s_*+(n-1)}\bigg) = n {\mathbb P}\bigg( R\ge \frac{\kappa-\eta}{n-1}\bigg) = 0. \end{align*}
We summarize our findings as
![]() ${\mathbb P}(Y_{Q,\gamma}(t)\ge \kappa t) \le Q^n D_\textrm{I}^{(n)}(\kappa-\varepsilon) t^{-(\gamma-1)n} (1+o(1))$
.
${\mathbb P}(Y_{Q,\gamma}(t)\ge \kappa t) \le Q^n D_\textrm{I}^{(n)}(\kappa-\varepsilon) t^{-(\gamma-1)n} (1+o(1))$
.
Letting
![]() $\varepsilon\searrow 0$
, we obtain
$\varepsilon\searrow 0$
, we obtain
![]() ${\mathbb P}(Y_{Q,\gamma}(t)\ge \kappa t) \le Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
, where
${\mathbb P}(Y_{Q,\gamma}(t)\ge \kappa t) \le Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
, where
 \begin{equation} D^{(n)}_\textrm{I}(\kappa) \;:\!=\; \lim_{\varepsilon\to 0} D^{(n)}_\textrm{I}(\kappa-\varepsilon) = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j). \end{equation}
\begin{equation} D^{(n)}_\textrm{I}(\kappa) \;:\!=\; \lim_{\varepsilon\to 0} D^{(n)}_\textrm{I}(\kappa-\varepsilon) = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j). \end{equation}
It is easy to see that for
![]() $n=1$
we obtain the same value of
$n=1$
we obtain the same value of
![]() $ D^{(1)}_\textrm{I}(\kappa)$
as in Theorem 3.
$ D^{(1)}_\textrm{I}(\kappa)$
as in Theorem 3.
For the lower bound, first, notice that
![]() $E_t$
in (18) is still negligible because by (20) we have
$E_t$
in (18) is still negligible because by (20) we have
![]() $E_t \le D_1 t v_0^{1-\gamma} = D_1 t (ht)^{1-\gamma} = O(t^{2-\gamma}) =o(t)$
. Hence, for every fixed small
$E_t \le D_1 t v_0^{1-\gamma} = D_1 t (ht)^{1-\gamma} = O(t^{2-\gamma}) =o(t)$
. Hence, for every fixed small
![]() $\varepsilon$
we may and do assume that
$\varepsilon$
we may and do assume that
![]() $E_t\le \varepsilon t$
for large t.
$E_t\le \varepsilon t$
for large t.
Second, using (19), by Chebyshev’s inequality we have, as
![]() $t\to\infty$
,
$t\to\infty$
,
Therefore, we may proceed towards the required lower bound as follows:
 \begin{align*} {\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa\,t) & \ge {\mathbb P}\big( |Y^\circ(t)|\le \varepsilon\,t, Y^{\dagger}(t)\ge (\kappa+2\varepsilon)t\big) \\[5pt] & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon\, t) {\mathbb P}\big( Y^{\dagger}(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big) \\[5pt] & = (1+o(1)) {\mathbb P}\big( Y^{\dagger}(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big). \end{align*}
\begin{align*} {\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa\,t) & \ge {\mathbb P}\big( |Y^\circ(t)|\le \varepsilon\,t, Y^{\dagger}(t)\ge (\kappa+2\varepsilon)t\big) \\[5pt] & \ge {\mathbb P}( |Y^\circ(t)|\le \varepsilon\, t) {\mathbb P}\big( Y^{\dagger}(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big) \\[5pt] & = (1+o(1)) {\mathbb P}\big( Y^{\dagger}(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big). \end{align*}
The idea behind this bound is to focus on n service processes providing a substantial large-deviation workload and to suppress other contributions.
Furthermore, by using the expression obtained while working on the upper bound,
 \begin{align*} {\mathbb P}\big(Y^{\dagger}&(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big) \\[5pt] & = \frac{Q^n}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa+2\varepsilon) \prod_{j=1}^n \nu({\textrm{d}} s_j) t^{-(\gamma-1)n} (1+o(1)) \\[5pt] & \;:\!=\; Q^n D_\textrm{I}^{(n)}(\kappa+2\varepsilon)t^{-(\gamma-1)n} (1+o(1)). \end{align*}
\begin{align*} {\mathbb P}\big(Y^{\dagger}&(t)\ge (\kappa+2\varepsilon) t;\; N_0=n\big) \\[5pt] & = \frac{Q^n}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa+2\varepsilon) \prod_{j=1}^n \nu({\textrm{d}} s_j) t^{-(\gamma-1)n} (1+o(1)) \\[5pt] & \;:\!=\; Q^n D_\textrm{I}^{(n)}(\kappa+2\varepsilon)t^{-(\gamma-1)n} (1+o(1)). \end{align*}
By letting
![]() $\varepsilon\searrow 0$
, we obtain
$\varepsilon\searrow 0$
, we obtain
 \begin{align*} \lim_{\varepsilon\searrow 0} D_\textrm{I}^{(n)}(\kappa+2\varepsilon) & = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n> \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j) \\[5pt] & = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j) = D_\textrm{I}^{(n)}(\kappa). \end{align*}
\begin{align*} \lim_{\varepsilon\searrow 0} D_\textrm{I}^{(n)}(\kappa+2\varepsilon) & = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n> \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j) \\[5pt] & = \frac{1}{n!} \int_{[0,1]^n} {\mathbb P}(s_1 R_1+\cdots+s_n R_n\ge \kappa) \prod_{j=1}^n \nu({\textrm{d}} s_j) = D_\textrm{I}^{(n)}(\kappa). \end{align*}
For the non-obvious passage we used the following lemma.
Lemma 2. Assume that (8) holds. Then
The required lower bound
![]() ${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \ge Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
now follows from the previous estimates. The proof is complete once the lemma is proved.
${\mathbb P}( Y_{Q,\gamma}(t)\ge \kappa t) \ge Q^n D^{(n)}_\textrm{I}(\kappa) t^{-(\gamma-1)n} (1+o(1))$
now follows from the previous estimates. The proof is complete once the lemma is proved.
Proof of Lemma
2. Let
![]() $r_1,\ldots,r_n$
be a sequence of atoms of the distribution
$r_1,\ldots,r_n$
be a sequence of atoms of the distribution
![]() $F_R$
, so that
$F_R$
, so that
![]() ${\mathbb P}(R=r_j)>0$
,
${\mathbb P}(R=r_j)>0$
,
![]() $1\le j\le n$
. Define
$1\le j\le n$
. Define
![]() $F = F(r_1,\ldots,r_n) \;:\!=\; \{ {\mathbf s}\in [0,1]^n\colon s_1r_1+\cdots+s_nr_n=\kappa \}$
.
$F = F(r_1,\ldots,r_n) \;:\!=\; \{ {\mathbf s}\in [0,1]^n\colon s_1r_1+\cdots+s_nr_n=\kappa \}$
.
For every subset of integers
![]() $J \subset \{1,\ldots,n\}$
let
$J \subset \{1,\ldots,n\}$
let
and notice that
![]() $[0,1]^n=\bigcup_{J} B_J$
. Let
$[0,1]^n=\bigcup_{J} B_J$
. Let
![]() $F_J\;:\!=\;F\bigcap B_J= \{{\mathbf s}\in B_J\colon \sum_{j\in J} s_j r_j = \kappa- \sum_{j\not\in J} r_j\}$
. If J is not empty, then
$F_J\;:\!=\;F\bigcap B_J= \{{\mathbf s}\in B_J\colon \sum_{j\in J} s_j r_j = \kappa- \sum_{j\not\in J} r_j\}$
. If J is not empty, then
![]() $\nu^n(F_J)=0$
because
$\nu^n(F_J)=0$
because
![]() $\nu$
is absolutely continuous on [0, 1).
$\nu$
is absolutely continuous on [0, 1).
If J is empty, then
![]() $B_J=\{(1,\ldots,1)\}$
is a singleton and
$B_J=\{(1,\ldots,1)\}$
is a singleton and
![]() $F_J=\emptyset$
, because otherwise
$F_J=\emptyset$
, because otherwise
![]() $\sum_{j=1}^n r_j=\kappa$
which would contradict (8). We conclude that
$\sum_{j=1}^n r_j=\kappa$
which would contradict (8). We conclude that
![]() $\nu^n\!\left( F(r_1,\ldots,r_n)\right)= \sum_J \nu^n(F_J) =0$
. Since
$\nu^n\!\left( F(r_1,\ldots,r_n)\right)= \sum_J \nu^n(F_J) =0$
. Since
![]() $\{{\mathbf s}\colon {\mathbb P}(s_1R_1+\cdots+s_nR_n=\kappa)>0\} \subset \bigcup_{r_1,\ldots,r_n} F(r_1,\ldots,r_n)$
and the union is countable, we obtain (32).
$\{{\mathbf s}\colon {\mathbb P}(s_1R_1+\cdots+s_nR_n=\kappa)>0\} \subset \bigcup_{r_1,\ldots,r_n} F(r_1,\ldots,r_n)$
and the union is countable, we obtain (32).
3.9. Proof of Theorem 5
Proof. For the upper bound, we take a small
![]() $\varepsilon>0$
, use the decomposition in (18) with
$\varepsilon>0$
, use the decomposition in (18) with
![]() $v_0\;:\!=\; h y_t$
(a small
$v_0\;:\!=\; h y_t$
(a small
![]() $h=h(\varepsilon)$
will be specified later on), and start with the usual bound
$h=h(\varepsilon)$
will be specified later on), and start with the usual bound
 \begin{align*} {\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) & \le {\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(Y^{\dagger}(t)\ge (1-\varepsilon) y_t) \\[5pt] & \le {\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(Y^{\dagger}(t)\ge (1-\varepsilon) y_t ;\; N_0=1) + P(N_0\ge 2). \end{align*}
\begin{align*} {\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) & \le {\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(Y^{\dagger}(t)\ge (1-\varepsilon) y_t) \\[5pt] & \le {\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) + {\mathbb P}(Y^{\dagger}(t)\ge (1-\varepsilon) y_t ;\; N_0=1) + P(N_0\ge 2). \end{align*}
To show that the first term is negligible compared to
![]() ${\bar F_R}(y_t/t)$
, we use the estimate in (28) with
${\bar F_R}(y_t/t)$
, we use the estimate in (28) with
![]() $z\;:\!=\;\varepsilon y_t$
,
$z\;:\!=\;\varepsilon y_t$
,
![]() $v_0\;:\!=\;hy_t$
and obtain, for some
$v_0\;:\!=\;hy_t$
and obtain, for some
![]() $C=C(\varepsilon,h)$
,
$C=C(\varepsilon,h)$
,
![]() ${\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) \le C(ty_t^{-\gamma})^{\frac{\varepsilon}{h}} \le C y_t^{-(\gamma-1)\,\frac{\varepsilon}{h}} \ll {\bar F_R}(y_t)\le {\bar F_R}(y_t/t)$
whenever h is chosen so small that
${\mathbb P}(Y^\circ(t)\ge \varepsilon y_t) \le C(ty_t^{-\gamma})^{\frac{\varepsilon}{h}} \le C y_t^{-(\gamma-1)\,\frac{\varepsilon}{h}} \ll {\bar F_R}(y_t)\le {\bar F_R}(y_t/t)$
whenever h is chosen so small that
![]() $(\gamma-1){\varepsilon}/{h}>m$
.
$(\gamma-1){\varepsilon}/{h}>m$
.
Subsequent evaluation of
![]() $Y^\dagger(t)$
requires analysis of the measure
$Y^\dagger(t)$
requires analysis of the measure
![]() $\mu^{(\ell,r)}_t$
. By using (12) and (10) we obtain
$\mu^{(\ell,r)}_t$
. By using (12) and (10) we obtain
 \begin{align*} \mu^{(\ell,r)}_t[v,\infty) & = \int_{v/t}^\infty \mu^{(\ell)}_t\bigg[\frac vr,t\bigg] F_R({\textrm{d}} r) \\[5pt] & = \int_{v/t}^\infty \bigg( \frac{t(r/v)^{\gamma}}{\gamma} +\frac{2-\gamma}{(\gamma-1)\gamma} (r/v)^{\gamma-1} \bigg)F_R({\textrm{d}} r) \\[5pt] & = \frac{tv^{-\gamma}}{\gamma} \int_{v/t}^\infty r^\gamma F_R({\textrm{d}} r) +\frac{(2-\gamma)v^{1-\gamma}}{(\gamma-1)\gamma} \int_{v/t}^\infty r^{\gamma-1} F_R({\textrm{d}} r). \end{align*}
\begin{align*} \mu^{(\ell,r)}_t[v,\infty) & = \int_{v/t}^\infty \mu^{(\ell)}_t\bigg[\frac vr,t\bigg] F_R({\textrm{d}} r) \\[5pt] & = \int_{v/t}^\infty \bigg( \frac{t(r/v)^{\gamma}}{\gamma} +\frac{2-\gamma}{(\gamma-1)\gamma} (r/v)^{\gamma-1} \bigg)F_R({\textrm{d}} r) \\[5pt] & = \frac{tv^{-\gamma}}{\gamma} \int_{v/t}^\infty r^\gamma F_R({\textrm{d}} r) +\frac{(2-\gamma)v^{1-\gamma}}{(\gamma-1)\gamma} \int_{v/t}^\infty r^{\gamma-1} F_R({\textrm{d}} r). \end{align*}
Since the tail of
![]() $F_R$
is regularly varying, we have the following asymptotics for the integrals as
$F_R$
is regularly varying, we have the following asymptotics for the integrals as
![]() $z\to \infty$
:
$z\to \infty$
:
 \begin{align*} \int_{z}^\infty r^\gamma F_R({\textrm{d}} r) & = \frac{m z^\gamma}{m-\gamma}{\bar F_R}(z) (1+o(1)), \\[5pt] \int_{z}^\infty r^{\gamma-1} F_R({\textrm{d}} r) & = \frac{m z^{\gamma-1}}{m-\gamma+1}{\bar F_R}(z) (1+o(1)) . \end{align*}
\begin{align*} \int_{z}^\infty r^\gamma F_R({\textrm{d}} r) & = \frac{m z^\gamma}{m-\gamma}{\bar F_R}(z) (1+o(1)), \\[5pt] \int_{z}^\infty r^{\gamma-1} F_R({\textrm{d}} r) & = \frac{m z^{\gamma-1}}{m-\gamma+1}{\bar F_R}(z) (1+o(1)) . \end{align*}
Therefore, we obtain
 \begin{align} \nonumber \mu^{(\ell,r)}_t[v,\infty) & = t^{-(\gamma-1) } \bigg [ \frac{m}{\gamma(m-\gamma)} + \frac{(2-\gamma)m}{(\gamma-1)\gamma(m-\gamma+1)} \bigg] {\bar F_R}(v/t) (1+o(1)) \\[5pt] \nonumber & = \frac{m(m-1)}{\gamma(\gamma-1)(m-\gamma+1)(m-\gamma)} t^{-(\gamma-1)} {\bar F_R}(v/t) (1+o(1)) \\[5pt] & = D t^{-(\gamma-1)} {\bar F_R}(v/t) (1+o(1)), \qquad \textrm{as } v\gg t. \end{align}
\begin{align} \nonumber \mu^{(\ell,r)}_t[v,\infty) & = t^{-(\gamma-1) } \bigg [ \frac{m}{\gamma(m-\gamma)} + \frac{(2-\gamma)m}{(\gamma-1)\gamma(m-\gamma+1)} \bigg] {\bar F_R}(v/t) (1+o(1)) \\[5pt] \nonumber & = \frac{m(m-1)}{\gamma(\gamma-1)(m-\gamma+1)(m-\gamma)} t^{-(\gamma-1)} {\bar F_R}(v/t) (1+o(1)) \\[5pt] & = D t^{-(\gamma-1)} {\bar F_R}(v/t) (1+o(1)), \qquad \textrm{as } v\gg t. \end{align}
Now the evaluation of
![]() $Y^\dagger$
is straightforward. Indeed, by (33),
$Y^\dagger$
is straightforward. Indeed, by (33),
 \begin{align*} {\mathbb P}\big(Y^{\dagger}(t)\ge (1-\varepsilon) y_t ;\; N_0=1\big) & \le Q \mu^{(\ell,r)}_t[(1-\varepsilon) y_t, \infty) \\[5pt] & = Q D t^{\gamma-1} {\bar F_R}((1-\varepsilon)y_t/t) (1+o(1)) \\[5pt] & = Q D t^{\gamma-1} {\bar F_R}(y_t/t) (1-\varepsilon)^{-m} (1+o(1)) , \end{align*}
\begin{align*} {\mathbb P}\big(Y^{\dagger}(t)\ge (1-\varepsilon) y_t ;\; N_0=1\big) & \le Q \mu^{(\ell,r)}_t[(1-\varepsilon) y_t, \infty) \\[5pt] & = Q D t^{\gamma-1} {\bar F_R}((1-\varepsilon)y_t/t) (1+o(1)) \\[5pt] & = Q D t^{\gamma-1} {\bar F_R}(y_t/t) (1-\varepsilon)^{-m} (1+o(1)) , \end{align*}
 \begin{align*} P(N_0\ge 2) \le Q^2 \mu^{(\ell,r)}_t[hy_t,\infty)^2 & = Q^2 (D t^{-(\gamma-1)} {\bar F_R}(hy_t/t))^2 (1+o(1)) \\[5pt] & = Q^2 (D t^{-(\gamma-1)} {\bar F_R}(y_t/t) h^{-m})^2 (1+o(1)) \\[5pt] & \ll t^{-(\gamma-1)} {\bar F_R}(y_t/t). \end{align*}
\begin{align*} P(N_0\ge 2) \le Q^2 \mu^{(\ell,r)}_t[hy_t,\infty)^2 & = Q^2 (D t^{-(\gamma-1)} {\bar F_R}(hy_t/t))^2 (1+o(1)) \\[5pt] & = Q^2 (D t^{-(\gamma-1)} {\bar F_R}(y_t/t) h^{-m})^2 (1+o(1)) \\[5pt] & \ll t^{-(\gamma-1)} {\bar F_R}(y_t/t). \end{align*}
By combining these estimates and letting
![]() $\varepsilon\to 0$
we obtain the desired bound,
$\varepsilon\to 0$
we obtain the desired bound,
For the lower bound, since
![]() $y_t\gg t \gg t^{1/\gamma}$
, all the bounds from Section 3.4 apply. For every
$y_t\gg t \gg t^{1/\gamma}$
, all the bounds from Section 3.4 apply. For every
![]() $\varepsilon>0$
, the inequality in (22) along with (33) yield
$\varepsilon>0$
, the inequality in (22) along with (33) yield
 \begin{align*} {\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) & \ge Q \mu^{(\ell,r)}_t[(1+2\varepsilon)y_t,\infty) (1+ o(1)) \\[5pt] & = Q D t^{-(\gamma-1)} (1+2\varepsilon)^{-m} {\bar F_R}(y_t/t) (1+o(1)), \end{align*}
\begin{align*} {\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) & \ge Q \mu^{(\ell,r)}_t[(1+2\varepsilon)y_t,\infty) (1+ o(1)) \\[5pt] & = Q D t^{-(\gamma-1)} (1+2\varepsilon)^{-m} {\bar F_R}(y_t/t) (1+o(1)), \end{align*}
and letting
![]() $\varepsilon\to 0$
we get the desired bound,
$\varepsilon\to 0$
we get the desired bound,
![]() ${\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) \ge Q D t^{-(\gamma-1)} {\bar F_R}(y_t/t) (1+o(1))$
.
${\mathbb P}(Y_{Q,\gamma}(t)\ge y_t) \ge Q D t^{-(\gamma-1)} {\bar F_R}(y_t/t) (1+o(1))$
.
Acknowledgement
We are very grateful to two anonymous referees for careful reading and useful advice.
Funding information
This work was supported by Russian Science Foundation grant 21-11-00047.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.