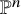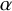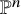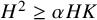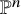1 Introduction
There are many competing notions of what it means for a variety to be ‘like’ projective space. Three of the most common are: rational, meaning birational to
![]() $\mathbb {P}^n$
; unirational, meaning admitting a dominant morphism from
$\mathbb {P}^n$
; unirational, meaning admitting a dominant morphism from
![]() $\mathbb {P}^n$
; and rationally connected, meaning for two general points, there exists a rational curve through both. Celebrated results of Griffiths-Harris, Artin-Mumford and Iskovskikh-Manin [Reference Clemens and GriffithsCG, Reference Artin and MumfordAM, Reference Iskovskikh and ManinIM] show that there are unirational varieties that are not rational. However, it remains an open question whether rationally connected varieties are always unirational.
$\mathbb {P}^n$
; and rationally connected, meaning for two general points, there exists a rational curve through both. Celebrated results of Griffiths-Harris, Artin-Mumford and Iskovskikh-Manin [Reference Clemens and GriffithsCG, Reference Artin and MumfordAM, Reference Iskovskikh and ManinIM] show that there are unirational varieties that are not rational. However, it remains an open question whether rationally connected varieties are always unirational.
Question 1.1. Does there exist a variety that is rationally connected but not unirational?
Due to the classification of surfaces, any counterexample would need to have dimension at least three. It is generally expected that the answer to Question 1.1 is yes, and an often-discussed source of examples is Fano hypersurfaces of large degree. A smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
is Fano if
$\mathbb {P}^n$
is Fano if
![]() $d\leq n$
, and every Fano variety is rationally connected. It is known that smooth hypersurfaces of degree d in
$d\leq n$
, and every Fano variety is rationally connected. It is known that smooth hypersurfaces of degree d in
![]() $\mathbb {P}^n$
are unirational when
$\mathbb {P}^n$
are unirational when
![]() $2^{d!} \leq n$
(see [Reference Behehsti and RiedlBR2] and [Reference Harris, Mazur and PandharipandeHMP]), but it is expected that very general hypersurfaces of large degree, specifically those with degree approximately n in
$2^{d!} \leq n$
(see [Reference Behehsti and RiedlBR2] and [Reference Harris, Mazur and PandharipandeHMP]), but it is expected that very general hypersurfaces of large degree, specifically those with degree approximately n in
![]() $\mathbb {P}^n$
, are not unirational. Schreieder [Reference SchreiederSch] has recently proved that the degree of a unirational parametrisation of a Fano hypersurface of large degree must be extremely large by showing that it should be divisible by every integer m such that
$\mathbb {P}^n$
, are not unirational. Schreieder [Reference SchreiederSch] has recently proved that the degree of a unirational parametrisation of a Fano hypersurface of large degree must be extremely large by showing that it should be divisible by every integer m such that
![]() $m \leq d - \log _2 n$
.
$m \leq d - \log _2 n$
.
Since any unirational variety will be swept out by rational surfaces, we can answer Question 1.1 negatively by finding a rationally connected variety that is not swept out by rational surfaces, as proposed by Kollár. To that end, there has been a lot of past work studying rational surfaces on Fano hypersurfaces. Testa [Reference TestaTe] generalises work of Beheshti and Starr [Reference Beheshti and StarrBS] and proves that a smooth complete intersection of index 1 is not swept out by rational surfaces S with
![]() $\omega _S$
nef. Observe that a rational curve in the space of rational curves on X corresponds to a rational surface in X. Beheshti [Reference BeheshtiBe] proves that spaces of rational curves of low degree are not uniruled, and in [Reference Beheshti and RiedlBR1] the authors generalise that work by showing that there are no rational surfaces in X ruled by low-degree rational curves, the generic one of which is smooth.
$\omega _S$
nef. Observe that a rational curve in the space of rational curves on X corresponds to a rational surface in X. Beheshti [Reference BeheshtiBe] proves that spaces of rational curves of low degree are not uniruled, and in [Reference Beheshti and RiedlBR1] the authors generalise that work by showing that there are no rational surfaces in X ruled by low-degree rational curves, the generic one of which is smooth.
In this paper, we prove several results restricting the types of rational surfaces that lie in a general hypersurface. Roughly speaking, we show that given a fixed surface or family of surfaces, a general Fano hypersurface of degree approximately n in
![]() $\mathbb {P}^n$
admits no generically finite maps from these surfaces. More precisely, we prove the following.
$\mathbb {P}^n$
admits no generically finite maps from these surfaces. More precisely, we prove the following.
Theorem 1.2. Let X be a hypersurface of degree d in
![]() $\mathbb {P}_{\mathbb {C}}^n$
. Then:
$\mathbb {P}_{\mathbb {C}}^n$
. Then:
-
1. (compare to Corollary 3.8) If
 $n \geq d> \frac {(2-\sqrt {2})(3n+k+1)}{2}+2$
and X is very general with respect to some fixed k-dimensional family of rational surfaces
$n \geq d> \frac {(2-\sqrt {2})(3n+k+1)}{2}+2$
and X is very general with respect to some fixed k-dimensional family of rational surfaces
 $\mathcal {S} \to B$
, then X admits no generically finite maps from a fibre of
$\mathcal {S} \to B$
, then X admits no generically finite maps from a fibre of
 $\mathcal {S} \to B$
. In particular, X contains no Hirzebruch surfaces, so there is no complete rational curve in the locus parametrising embedded smooth rational curves in the Kontsevich space
$\mathcal {S} \to B$
. In particular, X contains no Hirzebruch surfaces, so there is no complete rational curve in the locus parametrising embedded smooth rational curves in the Kontsevich space
 $\overline {\mathcal {M}}_{0,n}(X,e)$
.
$\overline {\mathcal {M}}_{0,n}(X,e)$
. -
2. (compare to Corollary 3.6) If
 $\alpha $
is a fixed positive number and
$\alpha $
is a fixed positive number and
 $\lambda < 1$
is fixed with
$\lambda < 1$
is fixed with
 $\lambda> \frac {3}{2}(2 - \sqrt {2})$
, then for sufficiently large n, a very general hypersurface of degree
$\lambda> \frac {3}{2}(2 - \sqrt {2})$
, then for sufficiently large n, a very general hypersurface of degree
 $d \geq n\lambda $
admits no generically finite morphisms from a rational surface S with
$d \geq n\lambda $
admits no generically finite morphisms from a rational surface S with
 $H \cdot K \leq \alpha H^2$
, where H is the pullback of the hyperplane class to S and K is the canonical class on S.
$H \cdot K \leq \alpha H^2$
, where H is the pullback of the hyperplane class to S and K is the canonical class on S.
For particular types of surfaces, we prove stronger restrictions. See Corollary 2.9 for a statement about del Pezzo surfaces and Corollary 2.11 for a statement about blowups of
![]() $\mathbb {P}^2$
at general points.
$\mathbb {P}^2$
at general points.
The basic idea of the proofs is to study the normal sheaf
![]() $N_{f/X}$
of a morphism f from a rational surface to X and understand the Euler characteristic of its twists. A direct calculation shows that
$N_{f/X}$
of a morphism f from a rational surface to X and understand the Euler characteristic of its twists. A direct calculation shows that
![]() $N_{f/X}(kH)$
must have negative Euler characteristic for small positive integers k. However, a careful analysis of globally generated sheaves on rational surfaces shows that in fact, this Euler characteristic must be positive. In Section 2, we lay out the core of this technique, working with twists of
$N_{f/X}(kH)$
must have negative Euler characteristic for small positive integers k. However, a careful analysis of globally generated sheaves on rational surfaces shows that in fact, this Euler characteristic must be positive. In Section 2, we lay out the core of this technique, working with twists of
![]() $N_{f/X}$
. This allows us to find d and n so that a very general degree d hypersurface X in
$N_{f/X}$
. This allows us to find d and n so that a very general degree d hypersurface X in
![]() $\mathbb {P}^n$
will not be swept out by rational surfaces with
$\mathbb {P}^n$
will not be swept out by rational surfaces with
![]() $H^2$
larger than some fixed multiple of
$H^2$
larger than some fixed multiple of
![]() $HK$
. In Section 3, we reduce mod p and apply a similar argument to the restricted tangent bundle
$HK$
. In Section 3, we reduce mod p and apply a similar argument to the restricted tangent bundle
![]() $f^* T_X$
. We show how techniques from [Reference Coskun and RiedlCR] then imply the statement of Theorem 1.2.
$f^* T_X$
. We show how techniques from [Reference Coskun and RiedlCR] then imply the statement of Theorem 1.2.
2 Families of rational surfaces
By a family of smooth rational surfaces, we mean a smooth and projective morphism
![]() $q: \mathcal S \to B$
such that B is a quasi-projective variety and the fibres of q are rational surfaces. Let X be a smooth hypersurface of degree
$q: \mathcal S \to B$
such that B is a quasi-projective variety and the fibres of q are rational surfaces. Let X be a smooth hypersurface of degree
![]() $d\leq n$
in
$d\leq n$
in
![]() $\mathbb {P}^n$
. Let S be a fibre of q and
$\mathbb {P}^n$
. Let S be a fibre of q and
![]() $f: S \to X$
a generically finite morphism. We denote by
$f: S \to X$
a generically finite morphism. We denote by
![]() $N_f$
the normal sheaf of f, which is the cokernel of the injective map
$N_f$
the normal sheaf of f, which is the cokernel of the injective map
![]() $T_S \to f^*T_X.$
To emphasise the range, we sometimes write
$T_S \to f^*T_X.$
To emphasise the range, we sometimes write
![]() $N_{f,X}$
instead of
$N_{f,X}$
instead of
![]() $N_f\!$
.
$N_f\!$
.
We start with a positivity result about the normal sheaf of f when X is a very general hypersurface. The result and technique come from work of Voisin [Reference VoisinVo96] and Pacienza [Reference PacienzaPa], although we give a proof for completeness.
Proposition 2.1. Let
![]() $\mathcal {X} \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
be the universal hypersurface on
$\mathcal {X} \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
be the universal hypersurface on
![]() $\mathbb {P}^n$
, and let
$\mathbb {P}^n$
, and let
![]() $q: \mathcal {S} \to B$
be a family of rational surfaces with morphisms
$q: \mathcal {S} \to B$
be a family of rational surfaces with morphisms
![]() $\phi :\mathcal {S} \to \mathcal {X}$
and
$\phi :\mathcal {S} \to \mathcal {X}$
and
![]() $g: B \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
commuting with the natural projection maps. Assume that
$g: B \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
commuting with the natural projection maps. Assume that
![]() $\phi $
is dominant and its restriction f to a general fibre
$\phi $
is dominant and its restriction f to a general fibre
![]() $S := \mathcal S_b$
of q is generically finite. Then
$S := \mathcal S_b$
of q is generically finite. Then
![]() $N_f$
is generically globally generated and
$N_f$
is generically globally generated and
![]() $N_f(H)$
is globally generated, where H is the pullback of the hyperplane section under f.
$N_f(H)$
is globally generated, where H is the pullback of the hyperplane section under f.
Proof. Let
![]() $f: S \to X$
be the restriction of
$f: S \to X$
be the restriction of
![]() $\phi $
to a general fibre of q. The fact that
$\phi $
to a general fibre of q. The fact that
![]() $N_f$
is generically globally generated follows from basic deformation theory and the fact that X is swept out by images of surfaces from this family. Indeed, let
$N_f$
is generically globally generated follows from basic deformation theory and the fact that X is swept out by images of surfaces from this family. Indeed, let
![]() $B_X=g^{-1}([X])$
and
$B_X=g^{-1}([X])$
and
![]() $\phi _X: \mathcal S_X\to X$
the restriction of
$\phi _X: \mathcal S_X\to X$
the restriction of
![]() $\phi $
to the fibre over
$\phi $
to the fibre over
![]() $B_X$
. Then
$B_X$
. Then
![]() $\phi _X$
is dominant by our assumption. So by generic smoothness, for a general point
$\phi _X$
is dominant by our assumption. So by generic smoothness, for a general point
![]() $(b,s)$
of
$(b,s)$
of
![]() $\mathcal S_X$
, the induced map on Zariski tangent spaces
$\mathcal S_X$
, the induced map on Zariski tangent spaces
![]() $T_{\mathcal S_X,(b,s)} \to T_{X,x}=f^*T_X|_s$
is surjective. Therefore the map
$T_{\mathcal S_X,(b,s)} \to T_{X,x}=f^*T_X|_s$
is surjective. Therefore the map
![]() $T_{\mathcal S_X,(b,s)} \to N_{f}|_s$
is surjective as well. There is a map from
$T_{\mathcal S_X,(b,s)} \to N_{f}|_s$
is surjective as well. There is a map from
![]() $T_{\mathcal S_X,(b,s)}$
to
$T_{\mathcal S_X,(b,s)}$
to
![]() $H^0(N_f)$
(see, for example, [Reference SernesiSe, Theorem 3.4.8]), and the map
$H^0(N_f)$
(see, for example, [Reference SernesiSe, Theorem 3.4.8]), and the map
![]() $T_{\mathcal S_X,(b,s)}\to N_{f}|_s$
factors through the map
$T_{\mathcal S_X,(b,s)}\to N_{f}|_s$
factors through the map
![]() $T_{\mathcal S_X,(b,s)} \to H^0(N_f)$
, so the desired result follows.
$T_{\mathcal S_X,(b,s)} \to H^0(N_f)$
, so the desired result follows.
For the second claim, we only use the assumption that for a general hypersurface X, there exists a generically finite morphism from a fibre of q to X.
We can take an étale base change
![]() $U \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
to obtain a family
$U \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
to obtain a family
![]() $\mathcal {X}_U \to U$
of hypersurfaces with a family
$\mathcal {X}_U \to U$
of hypersurfaces with a family
![]() $\mathcal {Y} \to U$
of rational surfaces parametrised by q mapping to fibres of
$\mathcal {Y} \to U$
of rational surfaces parametrised by q mapping to fibres of
![]() $\mathcal {X}_U \to U$
via a map
$\mathcal {X}_U \to U$
via a map
![]() $\psi : \mathcal {Y} \to \mathcal {X}_U$
such that
$\psi : \mathcal {Y} \to \mathcal {X}_U$
such that
![]() $\mathcal {Y}$
admits a natural
$\mathcal {Y}$
admits a natural
![]() $\operatorname {PGL}_{n+1}$
action. Denote by
$\operatorname {PGL}_{n+1}$
action. Denote by
![]() $\pi $
the projection map from
$\pi $
the projection map from
![]() $\mathcal X_U$
to
$\mathcal X_U$
to
![]() $\mathbb {P}^n$
, and let
$\mathbb {P}^n$
, and let
![]() $\pi ' = \pi \circ \psi $
. The induced map on tangent bundles
$\pi ' = \pi \circ \psi $
. The induced map on tangent bundles
![]() $T_{\mathcal {Y}} \to \pi ^{\prime *}T_{\mathbb {P}^n}$
is surjective because of the
$T_{\mathcal {Y}} \to \pi ^{\prime *}T_{\mathbb {P}^n}$
is surjective because of the
![]() $\operatorname {PGL}_{n+1}$
invariance of
$\operatorname {PGL}_{n+1}$
invariance of
![]() $\mathcal {Y}$
. We have the following commutative diagram:
$\mathcal {Y}$
. We have the following commutative diagram:

If u is a general point of U and
![]() $f: \mathcal Y_u \to \mathcal X_u$
is the restriction of
$f: \mathcal Y_u \to \mathcal X_u$
is the restriction of
![]() $\psi $
to the fibre over u, then
$\psi $
to the fibre over u, then
![]() $N_{\psi ,\mathcal X_U}|_{\mathcal Y_u} = N_{f, \mathcal X_u}$
, so to show
$N_{\psi ,\mathcal X_U}|_{\mathcal Y_u} = N_{f, \mathcal X_u}$
, so to show
![]() $N_{f, \mathcal X_u}(H)$
is globally generated, it is enough to show
$N_{f, \mathcal X_u}(H)$
is globally generated, it is enough to show
![]() $T_{\mathcal {X}_U/ \mathbb {P}^n} \otimes \pi ^*\mathcal {O}_{\mathbb {P}^n}(1)$
is globally generated. Consider the following diagram:
$T_{\mathcal {X}_U/ \mathbb {P}^n} \otimes \pi ^*\mathcal {O}_{\mathbb {P}^n}(1)$
is globally generated. Consider the following diagram:

Using the eight lemma and looking at the first column, it follows that
![]() $T_{\mathcal {X}_U/\mathbb {P}^n}$
is the kernel of the map
$T_{\mathcal {X}_U/\mathbb {P}^n}$
is the kernel of the map
![]() $\mathcal {O} \otimes S_d \to \pi ^*\mathcal {O}(d)$
. Such bundles are called Lazarsfeld-Mukai bundles, so we may say
$\mathcal {O} \otimes S_d \to \pi ^*\mathcal {O}(d)$
. Such bundles are called Lazarsfeld-Mukai bundles, so we may say
![]() $T_{\mathcal {X}_U/\mathbb {P}^n} \cong M_d$
, the pullback of the Lazarsfeld-Mukai bundle of
$T_{\mathcal {X}_U/\mathbb {P}^n} \cong M_d$
, the pullback of the Lazarsfeld-Mukai bundle of
![]() $\mathcal {O}_{\mathbb {P}^n}(d)$
.
$\mathcal {O}_{\mathbb {P}^n}(d)$
.
We can similarly define
![]() $M_1$
to be the kernel of the natural map
$M_1$
to be the kernel of the natural map
![]() $\mathcal {O} \otimes S_1 \to \pi ^*\mathcal {O}(1)$
. The bundle
$\mathcal {O} \otimes S_1 \to \pi ^*\mathcal {O}(1)$
. The bundle
![]() $M_d$
admits a surjection from a direct sum of copies of
$M_d$
admits a surjection from a direct sum of copies of
![]() $M_1$
, with maps given by multiplication by a general degree
$M_1$
, with maps given by multiplication by a general degree
![]() $d-1$
polynomial. It follows that
$d-1$
polynomial. It follows that
![]() $N_{h,\mathcal {X}_U}$
admits a surjection from a direct sum of copies of
$N_{h,\mathcal {X}_U}$
admits a surjection from a direct sum of copies of
![]() $M_1$
. Taking the second wedge power of the sequence
$M_1$
. Taking the second wedge power of the sequence
we see that
![]() $M_1(1)$
is globally generated, and hence
$M_1(1)$
is globally generated, and hence
![]() $M_d(1)$
is too, so the global generation result follows.
$M_d(1)$
is too, so the global generation result follows.
We will use the above proposition to give a lower bound on the Euler characteristic of the twists of the normal sheaf of f. To do so, we will need the following result.
Proposition 2.2. Let S be a rational surface over an algebraically closed field and
![]() $\pi : S \to \mathbb {P}^1$
a dominant morphism whose general fibres are isomorphic to
$\pi : S \to \mathbb {P}^1$
a dominant morphism whose general fibres are isomorphic to
![]() $\mathbb {P}^1$
. Let E be a coherent sheaf of rank m on S that is generically globally generated. Assume A and D are divisors on S such that A is nef and big, and
$\mathbb {P}^1$
. Let E be a coherent sheaf of rank m on S that is generically globally generated. Assume A and D are divisors on S such that A is nef and big, and
-
(a)
 $E(A)$
is globally generated,
$E(A)$
is globally generated, -
(b)
 $ \deg D|_C \geq \deg E|_C$
for a general fibre C of
$ \deg D|_C \geq \deg E|_C$
for a general fibre C of
 $\pi $
,
$\pi $
, -
(c)
 $H^1(\mathcal {O}_S(D))=0$
.
$H^1(\mathcal {O}_S(D))=0$
.
Then
![]() $\chi (E(A+D)) \geq m \; \chi (\mathcal {O}_S(A+D)).$
$\chi (E(A+D)) \geq m \; \chi (\mathcal {O}_S(A+D)).$
Proof. Since E is generically globally generated, choosing m general sections of E, we get an injective map
![]() $\mathcal {O}_S^m \to E$
. The cokernel of this map, denoted by T, is a torsion sheaf. Since
$\mathcal {O}_S^m \to E$
. The cokernel of this map, denoted by T, is a torsion sheaf. Since
![]() $E(A)$
is globally generated, there is a surjective map
$E(A)$
is globally generated, there is a surjective map
![]() $\mathcal {O}_S^l \to E(A)$
for some l. This in turn gives a surjective map
$\mathcal {O}_S^l \to E(A)$
for some l. This in turn gives a surjective map
![]() $\mathcal {O}_S^l \to T(A)$
whose kernel we denote by M.
$\mathcal {O}_S^l \to T(A)$
whose kernel we denote by M.

We claim
![]() $H^1( T(A+D)) = 0$
. By our assumption,
$H^1( T(A+D)) = 0$
. By our assumption,
![]() $H^1(\mathcal {O}_S(D)) =0$
, so applying the long exact sequence of cohomology to the first sequence twisted with
$H^1(\mathcal {O}_S(D)) =0$
, so applying the long exact sequence of cohomology to the first sequence twisted with
![]() $\mathcal {O}_S(D)$
, the claim follows if we show
$\mathcal {O}_S(D)$
, the claim follows if we show
![]() $H^2(M(D))) = 0$
. Applying the Leray spectral sequence corresponding to the map p, it is enough to show that
$H^2(M(D))) = 0$
. Applying the Leray spectral sequence corresponding to the map p, it is enough to show that
![]() $H^1(M(D)|_C)=0$
, where C is a general fibre of
$H^1(M(D)|_C)=0$
, where C is a general fibre of
![]() $\pi $
. Since C is a general fibre, the first short exact sequence above remains exacts after restricting to C, so
$\pi $
. Since C is a general fibre, the first short exact sequence above remains exacts after restricting to C, so
![]() $M|_C$
is torsion free. If
$M|_C$
is torsion free. If
![]() $M|_C = \mathcal {O}(a_1) \oplus \dots \oplus \mathcal {O}(a_l)$
, then since
$M|_C = \mathcal {O}(a_1) \oplus \dots \oplus \mathcal {O}(a_l)$
, then since
![]() $M|_C$
injects into
$M|_C$
injects into
![]() $\mathcal {O}_C^{ l}$
, we have
$\mathcal {O}_C^{ l}$
, we have
![]() $a_i \leq 0$
for each i. Also,
$a_i \leq 0$
for each i. Also,
 $$ \begin{align*}\sum_{i=1}^l a_i = - \deg (T(A))|_C = -\deg T|_C = -\deg E|_C\end{align*} $$
$$ \begin{align*}\sum_{i=1}^l a_i = - \deg (T(A))|_C = -\deg T|_C = -\deg E|_C\end{align*} $$
since
![]() $T|_C$
is torsion. If
$T|_C$
is torsion. If
![]() $a_i < -1-D \cdot C$
for some i, then
$a_i < -1-D \cdot C$
for some i, then
contradicting assumption (b). So
![]() $a_i \geq -1 - D \cdot C$
for every i and therefore
$a_i \geq -1 - D \cdot C$
for every i and therefore
![]() $H^1(M(D)|_C) =0$
.
$H^1(M(D)|_C) =0$
.
This shows that
![]() $H^1(T(A+D))=0$
, so
$H^1(T(A+D))=0$
, so
![]() $\chi (T(A+D)) \geq 0$
, and the desired result follows from the short exact sequence
$\chi (T(A+D)) \geq 0$
, and the desired result follows from the short exact sequence
Corollary 2.3. With the same assumptions as in Proposition 2.1,
Proof. By Proposition 2.1, for a general
![]() $f: S \to X$
,
$f: S \to X$
,
![]() $N_f$
is generically globally generated and
$N_f$
is generically globally generated and
![]() $N_f(H)$
is globally generated. We apply Proposition 2.2 to
$N_f(H)$
is globally generated. We apply Proposition 2.2 to
![]() $E=N_f$
,
$E=N_f$
,
![]() $D=(n+1-d)H+K$
and
$D=(n+1-d)H+K$
and
![]() $A=H$
. After possibly blowing up S at a point, we may assume there is a morphism
$A=H$
. After possibly blowing up S at a point, we may assume there is a morphism
![]() $\pi : S \to \mathbb {P}^1$
whose general fibres are smooth rational curves. Condition (a) of Proposition 2.2 is satisfied by our assumption. Since
$\pi : S \to \mathbb {P}^1$
whose general fibres are smooth rational curves. Condition (a) of Proposition 2.2 is satisfied by our assumption. Since
![]() $\deg N_f|_C = (n+1-d) H \cdot C - 2$
for a general fibre C of
$\deg N_f|_C = (n+1-d) H \cdot C - 2$
for a general fibre C of
![]() $\pi $
, condition (b) is satisfied. By the Kawamata-Viehweg vanishing theorem, condition (c) is also satisfied, so
$\pi $
, condition (b) is satisfied. By the Kawamata-Viehweg vanishing theorem, condition (c) is also satisfied, so
![]() $\chi (N_f((n+2-d)H+K)) \geq (n-3) \; \chi (\mathcal {O}_S(n+2-d)H+K).$
Applying the Riemann-Roch theorem, we get the desired inequality.
$\chi (N_f((n+2-d)H+K)) \geq (n-3) \; \chi (\mathcal {O}_S(n+2-d)H+K).$
Applying the Riemann-Roch theorem, we get the desired inequality.
In the next lemma, we calculate the Euler characteristics of the normal sheaf of
![]() $f: S \to X$
twisted with
$f: S \to X$
twisted with
![]() $tH+K$
directly.
$tH+K$
directly.
Lemma 2.4. Let X be a smooth hypersurface of degree d in
![]() $\mathbb {P}^n$
, and let
$\mathbb {P}^n$
, and let
![]() $f:S \to X$
be a morphism from a smooth rational surface S. If H denotes the pull-back of the hyperplane section, K the canonical divisor of S, and
$f:S \to X$
be a morphism from a smooth rational surface S. If H denotes the pull-back of the hyperplane section, K the canonical divisor of S, and
![]() $N_f$
the normal sheaf of f, then we have
$N_f$
the normal sheaf of f, then we have
 $$ \begin{align*} \begin{aligned} \chi(N_f(tH+K)) & = \frac{1}{2} ((n-3)t^2+2t(n+1-d)+n+1-d^2) \; H^2\\[3pt] &\quad + \frac{1}{2} (t(n-1)+n+1-d) \; H \cdot K \\[3pt] &\quad - K^2 +n+9. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \chi(N_f(tH+K)) & = \frac{1}{2} ((n-3)t^2+2t(n+1-d)+n+1-d^2) \; H^2\\[3pt] &\quad + \frac{1}{2} (t(n-1)+n+1-d) \; H \cdot K \\[3pt] &\quad - K^2 +n+9. \end{aligned} \end{align*} $$
Proof. This is a straightforward computation using the pullback of the Euler sequence on
![]() $\mathbb {P}^n$
and twisting it with
$\mathbb {P}^n$
and twisting it with
![]() $tH+K$
:
$tH+K$
:
and the short exact sequence
Theorem 2.5. With the same assumptions as in Proposition 2.1, we have
where K is the canonical divisor on S.
Corollary 2.6. Let
![]() $\alpha $
be a fixed positive number and
$\alpha $
be a fixed positive number and
![]() $\lambda $
be a number satisfying
$\lambda $
be a number satisfying
![]() $1> \lambda > 2-\sqrt {2}$
. Then for sufficiently large n, a very general hypersurface of degree
$1> \lambda > 2-\sqrt {2}$
. Then for sufficiently large n, a very general hypersurface of degree
![]() $d \geq \lambda n$
is not swept out by images of generically finite morphisms from a rational surface S with
$d \geq \lambda n$
is not swept out by images of generically finite morphisms from a rational surface S with
![]() $H \cdot K \leq \alpha H^2$
on S.
$H \cdot K \leq \alpha H^2$
on S.
To prove the corollary, we use Reider’s theorem [Reference ReiderRe].
Theorem 2.7. (Reider) Let X be a smooth projective surface and L a nef divisor on X with
![]() $L^2 \geq 5$
. If
$L^2 \geq 5$
. If
![]() $|L+K_X|$
has a base-point
$|L+K_X|$
has a base-point
![]() $x \in X$
, then there is an effective divisor D containing x satisfying
$x \in X$
, then there is an effective divisor D containing x satisfying
or
Proof of Corollary 2.6.
Suppose to the contrary that a very general hypersurface X is covered by images of such morphisms. Blowing down S, we can further assume
![]() $f: S \to X$
does not contract any
$f: S \to X$
does not contract any
![]() $(-1)$
-curve. Applying Theorem 2.5 to the hypotheses given, we conclude that there is a generically finite morphism
$(-1)$
-curve. Applying Theorem 2.5 to the hypotheses given, we conclude that there is a generically finite morphism
![]() $f: S \to X$
that does not contract any
$f: S \to X$
that does not contract any
![]() $(-1)$
-curve and satisfies the inequality of Theorem 2.5. Since H is nef, applying Reider’s theorem to
$(-1)$
-curve and satisfies the inequality of Theorem 2.5. Since H is nef, applying Reider’s theorem to
![]() $3H$
, we see that
$3H$
, we see that
![]() $3H+K$
is base-point free. Therefore
$3H+K$
is base-point free. Therefore
![]() $(3H+K)^2\geq 0$
, so
$(3H+K)^2\geq 0$
, so
![]() $-2K^2 \leq 18H^2+12H \cdot K$
. Since
$-2K^2 \leq 18H^2+12H \cdot K$
. Since
![]() $d \geq \lambda b$
and
$d \geq \lambda b$
and
![]() $\lambda> 2-\sqrt {2}$
, the coefficient of
$\lambda> 2-\sqrt {2}$
, the coefficient of
![]() $H^2$
in 2.1 becomes arbitrarily negative compared to the coefficient of
$H^2$
in 2.1 becomes arbitrarily negative compared to the coefficient of
![]() $H \cdot K$
, so we get a contradiction.
$H \cdot K$
, so we get a contradiction.
Remark 2.8. Unfortunately, there exist examples of rational surfaces containing divisors H with
![]() $H^2$
small relative to
$H^2$
small relative to
![]() $H \cdot K$
.
$H \cdot K$
.
Take a general pencil of degree b curves in
![]() $\mathbb {P}^2$
, and let S be the blowup of
$\mathbb {P}^2$
, and let S be the blowup of
![]() $\mathbb {P}^2$
along the
$\mathbb {P}^2$
along the
![]() $b^2$
base points of the pencil. Let
$b^2$
base points of the pencil. Let
![]() $H = (b+1)L - \sum _i E_i$
, where the sum ranges over all of the exceptional divisors. Then H is base-point free and big. Moreover,
$H = (b+1)L - \sum _i E_i$
, where the sum ranges over all of the exceptional divisors. Then H is base-point free and big. Moreover,
![]() $H^2 = (b+1)^2 - b^2 = 2b+1$
, while
$H^2 = (b+1)^2 - b^2 = 2b+1$
, while
![]() $H \cdot K = -3b + b^2 = b(b-3)$
. Thus,
$H \cdot K = -3b + b^2 = b(b-3)$
. Thus,
![]() $H \cdot K$
grows faster than
$H \cdot K$
grows faster than
![]() $H^2$
as b becomes large, and so we cannot hope to obtain a linear bound for
$H^2$
as b becomes large, and so we cannot hope to obtain a linear bound for
![]() $H \cdot K$
in terms of
$H \cdot K$
in terms of
![]() $H^2$
.
$H^2$
.
For another example, consider Example 2 from [Reference Ciliberto, Knutsen, Lesieutre, Lozovanu, Miranda, Mustopa and TestaCKLLMMT]. The authors describe a blowup S of
![]() $\mathbb {P}^2$
at 19 points together with a sequence of big and nef divisors
$\mathbb {P}^2$
at 19 points together with a sequence of big and nef divisors
![]() $D_n$
such that
$D_n$
such that
![]() $K_S \cdot D_n$
goes to infinity while
$K_S \cdot D_n$
goes to infinity while
![]() $D_n^2 = 2$
for all n.
$D_n^2 = 2$
for all n.
Corollary 2.9. If X is a very general hypersurface in
![]() $\mathbb {P}_{\mathbb {C}}^n$
of degree
$\mathbb {P}_{\mathbb {C}}^n$
of degree
![]() $d> (2-\sqrt {2})n+3$
, then the images of generically finite morphisms from del Pezzo surfaces to X cannot sweep out X.
$d> (2-\sqrt {2})n+3$
, then the images of generically finite morphisms from del Pezzo surfaces to X cannot sweep out X.
We remark that
![]() $2-\sqrt {2} \approx .59$
, so the result holds for
$2-\sqrt {2} \approx .59$
, so the result holds for
![]() $d> \frac {3n}{5}+3$
.
$d> \frac {3n}{5}+3$
.
Proof. Suppose to the contrary that X is covered by images of generically finite morphisms from del Pezzo surfaces. Then by Theorem 2.5, there exist a del Pezzo surface S and a generically finite morphism
![]() $f: S \to X$
for which inequality (2.1) holds. We show that this is not possible. Let B be the coefficient of
$f: S \to X$
for which inequality (2.1) holds. We show that this is not possible. Let B be the coefficient of
![]() $H^2$
in inequality (2.1). We first show
$H^2$
in inequality (2.1). We first show
![]() $B < -5n-4$
. To see this, note that since
$B < -5n-4$
. To see this, note that since
![]() $d> (2-\sqrt {2})n+3$
,
$d> (2-\sqrt {2})n+3$
,
![]() $n-d < (\sqrt {2}-1)n-3$
, so
$n-d < (\sqrt {2}-1)n-3$
, so
Since S is a del Pezzo surface,
![]() $-K$
is effective, so
$-K$
is effective, so
![]() $H \cdot K < 0$
and
$H \cdot K < 0$
and
![]() $K^2> 0$
. So the left-hand side of inequality (2.1) is at most
$K^2> 0$
. So the left-hand side of inequality (2.1) is at most
![]() $-5n-4-(3n-3d+5)-2+24$
, which is negative since
$-5n-4-(3n-3d+5)-2+24$
, which is negative since
![]() $d \leq n$
and
$d \leq n$
and
![]() $n \geq 3$
. This gives a contradiction.
$n \geq 3$
. This gives a contradiction.
Next we apply Theorem 2.5 to the blow-up of
![]() $\mathbb {P}^2$
in general points. Recall the following conjecture of Harbourne and Hirschowitz [Reference HarbourneHar] and [Reference HirschowitzHi].
$\mathbb {P}^2$
in general points. Recall the following conjecture of Harbourne and Hirschowitz [Reference HarbourneHar] and [Reference HirschowitzHi].
Conjecture 2.10 (Harbourne-Hirschowitz).
Let S be the blow-up of
![]() $\mathbb {P}^2$
at k general points and L a line bundle on S. Then
$\mathbb {P}^2$
at k general points and L a line bundle on S. Then
![]() $h^1(L) \neq 0$
if and only if there is a
$h^1(L) \neq 0$
if and only if there is a
![]() $(-1)$
-curve E in S such that
$(-1)$
-curve E in S such that
It is known that the Harbourne-Hirschowitz conjecture holds for
![]() $m\leq 9$
[Reference CilbertoCi, Theorem 5.1].
$m\leq 9$
[Reference CilbertoCi, Theorem 5.1].
Corollary 2.11. Suppose
![]() $d> (2-\sqrt {2})n+4$
,
$d> (2-\sqrt {2})n+4$
,
![]() $n \geq 4$
, and X is a very general hypersurface of degree d in
$n \geq 4$
, and X is a very general hypersurface of degree d in
![]() $\mathbb {P}_{\mathbb {C}}^n$
. If the Harbourne-Hirschowitz Conjecture holds true, then the images of generically finite morphisms from blow-ups of
$\mathbb {P}_{\mathbb {C}}^n$
. If the Harbourne-Hirschowitz Conjecture holds true, then the images of generically finite morphisms from blow-ups of
![]() $\mathbb {P}^2$
in general points do not cover X.
$\mathbb {P}^2$
in general points do not cover X.
Proof. Suppose to the contrary that a very general hypersurface X of degree d is covered by the images of generically finite morphisms from blowups of
![]() $\mathbb {P}^2$
in general points. Then by Theorem 2.5, there is a rational surface S obtained by blowing up
$\mathbb {P}^2$
in general points. Then by Theorem 2.5, there is a rational surface S obtained by blowing up
![]() $\mathbb {P}^2$
in general points and a generically finite morphism
$\mathbb {P}^2$
in general points and a generically finite morphism
![]() $f: S \to X$
such that inequality (2.1) is satisfied. We can assume f does not contract any
$f: S \to X$
such that inequality (2.1) is satisfied. We can assume f does not contract any
![]() $(-1)$
-curve, since otherwise we can consider the induced morphism from the blow-down of S to X instead. By the Harbourne-Hirschowitz conjecture,
$(-1)$
-curve, since otherwise we can consider the induced morphism from the blow-down of S to X instead. By the Harbourne-Hirschowitz conjecture,
![]() $H^1(S,\mathcal {O}_S(H))=0$
, so by the Riemann-Roch theorem,
$H^1(S,\mathcal {O}_S(H))=0$
, so by the Riemann-Roch theorem,
![]() $H(H-K) =2\chi (H) -2\geq -2$
. Therefore
$H(H-K) =2\chi (H) -2\geq -2$
. Therefore
![]() $H \cdot K \leq H^2+2$
.
$H \cdot K \leq H^2+2$
.
By [Reference Riedl and YangRY, Theorem 2.3], if
![]() $n < \frac {d^2+3d+6}{6}$
, then there is no rational curve on the space of lines in X. Our assumption on the degree implies this inequality is satisfied, so we can assume the image of S under f is not covered by a pencil of lines. In particular, the image of S has degree at least
$n < \frac {d^2+3d+6}{6}$
, then there is no rational curve on the space of lines in X. Our assumption on the degree implies this inequality is satisfied, so we can assume the image of S under f is not covered by a pencil of lines. In particular, the image of S has degree at least
![]() $2$
, so
$2$
, so
![]() $H^2 \geq 2$
. Since the image of S is not covered by lines, and since H is big and nef, by Reider’s theorem [Reference ReiderRe],
$H^2 \geq 2$
. Since the image of S is not covered by lines, and since H is big and nef, by Reider’s theorem [Reference ReiderRe],
![]() $2H+K$
is base-point free. Therefore
$2H+K$
is base-point free. Therefore
![]() $(2H+K)^2\geq 0$
, so
$(2H+K)^2\geq 0$
, so
![]() $-2K^2 \leq 8H^2+8H \cdot K \leq 16H^2+16$
. So if we denote the left-hand side of inequality 2.1 by A, then we have
$-2K^2 \leq 8H^2+8H \cdot K \leq 16H^2+16$
. So if we denote the left-hand side of inequality 2.1 by A, then we have
Denote the coefficient of
![]() $H^2$
in the above inequality by B. We claim
$H^2$
in the above inequality by B. We claim
![]() $B < -(3n-3d+5)-20$
. This is because by our assumption
$B < -(3n-3d+5)-20$
. This is because by our assumption
![]() $n-d \leq (\sqrt {2}-1)n-4$
, so
$n-d \leq (\sqrt {2}-1)n-4$
, so
 $$ \begin{align*} \begin{aligned} B + (3n-3d+5)+20 &< 2((\sqrt{2}-1)n-3)((\sqrt{2}-1)n-2)+n+1-((2-\sqrt{2})n+4)^2 \\ & \;\;\;\;\; +6((\sqrt{2}-1)n-4) +46 \\ & = (4\sqrt{2}-11)n+19\\ & <0, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} B + (3n-3d+5)+20 &< 2((\sqrt{2}-1)n-3)((\sqrt{2}-1)n-2)+n+1-((2-\sqrt{2})n+4)^2 \\ & \;\;\;\;\; +6((\sqrt{2}-1)n-4) +46 \\ & = (4\sqrt{2}-11)n+19\\ & <0, \end{aligned} \end{align*} $$
where the last line follows from the assumption
![]() $n \geq 4$
. Since
$n \geq 4$
. Since
![]() $H^2 \geq 2$
, we get
$H^2 \geq 2$
, we get
![]() $A <0$
, a contradiction.
$A <0$
, a contradiction.
3 Morphisms from a fixed rational surface
Here we consider maps from a fixed rational surface S. Let S be a smooth rational surface, and let
![]() $\operatorname {Hom}^0(S,X)$
denote the open locus in
$\operatorname {Hom}^0(S,X)$
denote the open locus in
![]() $\operatorname {Hom}(S,X)$
parametrising generically finite morphisms from S to X. We say that S strongly sweeps out a variety X if the natural map
$\operatorname {Hom}(S,X)$
parametrising generically finite morphisms from S to X. We say that S strongly sweeps out a variety X if the natural map
![]() $\operatorname {Hom}^0(S,X) \times S \to X \times S$
given by
$\operatorname {Hom}^0(S,X) \times S \to X \times S$
given by
![]() $(f,p) \mapsto (f(p), p)$
is dominant. In other words, X is strongly swept out by S if for any pair of a general points
$(f,p) \mapsto (f(p), p)$
is dominant. In other words, X is strongly swept out by S if for any pair of a general points
![]() $p \in S$
and
$p \in S$
and
![]() $q \in X$
, there is a generically finite morphism
$q \in X$
, there is a generically finite morphism
![]() $S \to X$
sending p to q.
$S \to X$
sending p to q.
Proposition 3.1. Suppose that X is a very general hypersurface of degree d in
![]() $\mathbb {P}_{\mathbb {C}}^n$
and X is strongly swept out by S. Then there is
$\mathbb {P}_{\mathbb {C}}^n$
and X is strongly swept out by S. Then there is
![]() $f \in \operatorname {Hom}^0(S,X)$
such that
$f \in \operatorname {Hom}^0(S,X)$
such that
![]() $f^* T_X$
is generically globally generated and
$f^* T_X$
is generically globally generated and
![]() $f^*T_X(H)$
is globally generated.
$f^*T_X(H)$
is globally generated.
Proof. Consider the map
![]() $\operatorname {Hom^0}(S,X) \times S \to X \times S$
. Then for any
$\operatorname {Hom^0}(S,X) \times S \to X \times S$
. Then for any
![]() $(f,p) \in \operatorname {Hom}^0(S,X) \times S$
, we have the following diagram:
$(f,p) \in \operatorname {Hom}^0(S,X) \times S$
, we have the following diagram:

Let
![]() $(p,f)$
be a general point of an irreducible component of
$(p,f)$
be a general point of an irreducible component of
![]() $\operatorname {Hom}^0(S,X) \times S$
that dominates
$\operatorname {Hom}^0(S,X) \times S$
that dominates
![]() $X \times S$
. Then if
$X \times S$
. Then if
![]() $\mathcal {U}_{red}$
is the largest reduced subscheme of
$\mathcal {U}_{red}$
is the largest reduced subscheme of
![]() $\operatorname {Hom}^0(S,X)$
, generic smoothness shows that
$\operatorname {Hom}^0(S,X)$
, generic smoothness shows that
![]() $\alpha |_{T_{\mathcal {U}_{red},(p,f)}}$
is surjective, and hence
$\alpha |_{T_{\mathcal {U}_{red},(p,f)}}$
is surjective, and hence
![]() $\pi _2 \circ \alpha $
is surjective. It follows that
$\pi _2 \circ \alpha $
is surjective. It follows that
![]() $\beta $
is surjective, and hence
$\beta $
is surjective, and hence
![]() $f^*T_X$
is generically globally generated.
$f^*T_X$
is generically globally generated.
To prove
![]() $f^*T_X(H)$
is globally generated, we repeat the argument of Proposition 2.1 with
$f^*T_X(H)$
is globally generated, we repeat the argument of Proposition 2.1 with
![]() $\mathcal {X}$
replaced by
$\mathcal {X}$
replaced by
![]() $\mathcal {X} \times S$
. We can find a dominant morphism
$\mathcal {X} \times S$
. We can find a dominant morphism
![]() $U \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
and a morphism
$U \to H^0(\mathcal {O}_{\mathbb {P}^n}(d))$
and a morphism
![]() $\psi : U \times S \to \mathcal {X}_U \times S$
such that if
$\psi : U \times S \to \mathcal {X}_U \times S$
such that if
![]() $\pi ': U \times S \to \mathbb {P}^n$
is the natural morphism, then the induced map on tangent spaces
$\pi ': U \times S \to \mathbb {P}^n$
is the natural morphism, then the induced map on tangent spaces
![]() $T_{U \times S} \to \pi ^{\prime *} T_{\mathbb {P}^n\times S}$
is surjective. The same argument as in Proposition 2.1 shows that
$T_{U \times S} \to \pi ^{\prime *} T_{\mathbb {P}^n\times S}$
is surjective. The same argument as in Proposition 2.1 shows that
![]() $T_{\mathcal {X}_U \times S / \mathbb {P}^n \times S}(H)$
is globally generated, and therefore
$T_{\mathcal {X}_U \times S / \mathbb {P}^n \times S}(H)$
is globally generated, and therefore
![]() $N_{\psi , \mathcal {X}_U \times S}(H)$
is globally generated. If
$N_{\psi , \mathcal {X}_U \times S}(H)$
is globally generated. If
![]() $f: S \to X$
is the restriction of
$f: S \to X$
is the restriction of
![]() $\psi $
to
$\psi $
to
![]() $\{u\}\times S$
for a general point u of U, then
$\{u\}\times S$
for a general point u of U, then
![]() $N_{\psi , \mathcal {X}_U \times S}|_{u \times S} = N_{f, X \times S} = f^*T_X$
, and the desired result follows.
$N_{\psi , \mathcal {X}_U \times S}|_{u \times S} = N_{f, X \times S} = f^*T_X$
, and the desired result follows.
Proposition 3.2. Suppose S is a fixed rational surface. If
![]() $d> (2-\sqrt {2})n+2$
and X is a very general hypersurface of degree d in
$d> (2-\sqrt {2})n+2$
and X is a very general hypersurface of degree d in
![]() $\mathbb {P}_{\mathbb {C}}^n$
, then X is not strongly swept out by S.
$\mathbb {P}_{\mathbb {C}}^n$
, then X is not strongly swept out by S.
Proof. Assume to the contrary that X is strongly swept out by S. Then by Proposition 3.1, there is
![]() $f:S \to X$
such that
$f:S \to X$
such that
![]() $f^*T_X$
is generically globally generated and
$f^*T_X$
is generically globally generated and
![]() $f^*T_X(H)$
is globally generated. Passing to finite characteristic, we can assume there is a sufficiently large prime number p, a rational surface
$f^*T_X(H)$
is globally generated. Passing to finite characteristic, we can assume there is a sufficiently large prime number p, a rational surface
![]() $S_p$
, a smooth hypersurface
$S_p$
, a smooth hypersurface
![]() $X_p$
of degree d and a morphism
$X_p$
of degree d and a morphism
![]() $f_p:S_p\to X_p$
, all defined over an algebraically closed field of characteristic p such that
$f_p:S_p\to X_p$
, all defined over an algebraically closed field of characteristic p such that
![]() $f_p^*T_{X_p}$
is generically globally generated and
$f_p^*T_{X_p}$
is generically globally generated and
![]() $f_p^*T_{X_p}(H)$
is globally generated.
$f_p^*T_{X_p}(H)$
is globally generated.
For a coherent sheaf F on
![]() $S_p$
, let
$S_p$
, let
![]() $F^{(p)}$
denote the pullback of F under the absolute Frobenius morphism of X (see [Reference HartshorneHa, Proposition 6.1]). Since
$F^{(p)}$
denote the pullback of F under the absolute Frobenius morphism of X (see [Reference HartshorneHa, Proposition 6.1]). Since
![]() $f_p^*T_{X_p}(H)$
is globally generated,
$f_p^*T_{X_p}(H)$
is globally generated,
![]() $(f_p^*T_{X_p})^{(p)}(pH)$
is also globally generated. Since
$(f_p^*T_{X_p})^{(p)}(pH)$
is also globally generated. Since
![]() $f_p^*T_{X_p}$
is generically globally generated,
$f_p^*T_{X_p}$
is generically globally generated,
![]() $(f_p^*T_{X_p})^{(p)}$
will be as well. Let K denote the canonical divisor of
$(f_p^*T_{X_p})^{(p)}$
will be as well. Let K denote the canonical divisor of
![]() $S_p$
. A similar computation as in Lemma 2.4 shows that
$S_p$
. A similar computation as in Lemma 2.4 shows that
We can now apply Proposition 2.2 with
![]() $E=f_p^*T_{X_p}^{(p)}$
,
$E=f_p^*T_{X_p}^{(p)}$
,
![]() $A =pH$
and
$A =pH$
and
![]() $D=p(n+2-d)H+K$
to get a contradiction. Since
$D=p(n+2-d)H+K$
to get a contradiction. Since
![]() $S_p$
is a rational surface, by [Reference MukaiMu, Theorem 3],
$S_p$
is a rational surface, by [Reference MukaiMu, Theorem 3],
![]() $H^1(D+pH)=0$
, so condition (c) of Proposition 2.2 is satisfied. After possibly blowing up
$H^1(D+pH)=0$
, so condition (c) of Proposition 2.2 is satisfied. After possibly blowing up
![]() $S_p$
at a point, we can assume there is a morphism
$S_p$
at a point, we can assume there is a morphism
![]() $S_p \to \mathbb {P}^1$
whose general fibres are smooth rational curves. If C denotes a general fibre of this morphism, then
$S_p \to \mathbb {P}^1$
whose general fibres are smooth rational curves. If C denotes a general fibre of this morphism, then
![]() $\deg (f_p^*T_{X_p}^{(p)})|_C = p(n+1-d) H \cdot C \leq p(n+2-d)H\cdot C -2$
, so condition (b) is also satisfied. Therefore,
$\deg (f_p^*T_{X_p}^{(p)})|_C = p(n+1-d) H \cdot C \leq p(n+2-d)H\cdot C -2$
, so condition (b) is also satisfied. Therefore,
 $$ \begin{align*} \begin{aligned} \chi(f_p^*T_{X_p}^{(p)}((n+3-d)pH+K)) & \geq (n-1) \chi (\mathcal{O}_{S_p}((n+3-d)pH+K))\\ & = \frac{1}{2}(p^2(n-1)(n+3-d)^2 H^2+p(n-1)(n+3-d)HK)+ (n-1). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \chi(f_p^*T_{X_p}^{(p)}((n+3-d)pH+K)) & \geq (n-1) \chi (\mathcal{O}_{S_p}((n+3-d)pH+K))\\ & = \frac{1}{2}(p^2(n-1)(n+3-d)^2 H^2+p(n-1)(n+3-d)HK)+ (n-1). \end{aligned} \end{align*} $$
Comparing the coefficients of
![]() $H^2$
in this equation and Equation (3.1) when
$H^2$
in this equation and Equation (3.1) when
![]() $t=n+3-d$
, and letting p increase, we see if the above inequality holds, then we must have
$t=n+3-d$
, and letting p increase, we see if the above inequality holds, then we must have
Letting
![]() $t=n+3-d$
, this gives
$t=n+3-d$
, this gives
But since we assume
![]() $d> (2-\sqrt {2})n+2$
, we have
$d> (2-\sqrt {2})n+2$
, we have
![]() $n-d < (\sqrt {2}-1)n-2$
, so the left-hand side of the above inequality is smaller than
$n-d < (\sqrt {2}-1)n-2$
, so the left-hand side of the above inequality is smaller than
a contradiction.
We now implement a technique from [Reference Coskun and RiedlCR] to show that a very general X admits no generically finite morphisms from S. We recall some terminology. Let
![]() $\mathcal {U}_{n,d}$
be the space of pairs
$\mathcal {U}_{n,d}$
be the space of pairs
![]() $(p,X)$
, where X is a degree d hypersurface in
$(p,X)$
, where X is a degree d hypersurface in
![]() $\mathbb {P}^n$
and
$\mathbb {P}^n$
and
![]() $p \in X \subset \mathbb {P}^n$
. Given a subset
$p \in X \subset \mathbb {P}^n$
. Given a subset
![]() $\mathcal {B}_r \subset \mathcal {U}_{r,d}$
, we let the tower of induced varieties of
$\mathcal {B}_r \subset \mathcal {U}_{r,d}$
, we let the tower of induced varieties of
![]() $\mathcal {B}_r$
be defined inductively by
$\mathcal {B}_r$
be defined inductively by
![]() $\mathcal {B}_{j+1} \subset \mathcal {U}_{j+1,d}$
is the set of pairs
$\mathcal {B}_{j+1} \subset \mathcal {U}_{j+1,d}$
is the set of pairs
![]() $(p,X)$
such that some linear section of the pair
$(p,X)$
such that some linear section of the pair
![]() $(p,X)$
is in
$(p,X)$
is in
![]() $\mathcal {B}_j$
,
$\mathcal {B}_j$
,
![]() $j \geq r$
.
$j \geq r$
.
In our setting, we are interested in proving that
![]() $\mathcal {B}_n$
has high codimension in
$\mathcal {B}_n$
has high codimension in
![]() $\mathcal {U}_{n,d}$
, from which it will follow that a very general hypersurface will contain no points of
$\mathcal {U}_{n,d}$
, from which it will follow that a very general hypersurface will contain no points of
![]() $\mathcal {B}_n$
. The tool we use is the following.
$\mathcal {B}_n$
. The tool we use is the following.
Theorem 3.3 (Theorem 4.8 from [Reference Coskun and RiedlCR]).
Let
![]() $\mathcal {B}_r \subset \mathcal {U}_{r,d}$
be an integral,
$\mathcal {B}_r \subset \mathcal {U}_{r,d}$
be an integral,
![]() $PGL_{r+1}$
-invariant subvariety, and let
$PGL_{r+1}$
-invariant subvariety, and let
![]() $\mathcal {B}_{n}, n \geq r,$
be the tower of induced subvarieties of
$\mathcal {B}_{n}, n \geq r,$
be the tower of induced subvarieties of
![]() $\mathcal {B}_r$
. Then if
$\mathcal {B}_r$
. Then if
![]() $\mathcal {B}_m$
is not dense in
$\mathcal {B}_m$
is not dense in
![]() $\mathcal {U}_{m,d}$
for some
$\mathcal {U}_{m,d}$
for some
![]() $m> r$
, either
$m> r$
, either
-
1.
 $\operatorname {codim} \mathcal {B}_n \subset \mathcal {U}_{n,d}$
is at least
$\operatorname {codim} \mathcal {B}_n \subset \mathcal {U}_{n,d}$
is at least
 $2(m-n)+1$
for every
$2(m-n)+1$
for every
 $r \leq n \leq m$
, or
$r \leq n \leq m$
, or -
2. there is some
 $\mathcal {B}_1 \subset \mathcal {U}_{1,d}$
such that
$\mathcal {B}_1 \subset \mathcal {U}_{1,d}$
such that
 $\mathcal {B}_n$
is in the closure of the tower of induced subvarieties of
$\mathcal {B}_n$
is in the closure of the tower of induced subvarieties of
 $\mathcal {B}_1$
, or
$\mathcal {B}_1$
, or -
3.
 $\mathcal {B}_{m,d}$
is the space of pairs
$\mathcal {B}_{m,d}$
is the space of pairs
 $(p,X)$
with p contained in a line
$(p,X)$
with p contained in a line
 $\ell $
lying in X.
$\ell $
lying in X.
We wish to show that in our setting, we need only consider case (1).
Corollary 3.4. Let
![]() $\mathcal {B}_r \subset \mathcal {U}_{r,d}$
be an integral,
$\mathcal {B}_r \subset \mathcal {U}_{r,d}$
be an integral,
![]() $PGL_{r+1}$
-invariant subvariety, and let
$PGL_{r+1}$
-invariant subvariety, and let
![]() $\mathcal {B}_{n,d}$
be the tower of induced subvarieties of
$\mathcal {B}_{n,d}$
be the tower of induced subvarieties of
![]() $\mathcal {B}_r$
for
$\mathcal {B}_r$
for
![]() $n \geq r$
. Then if
$n \geq r$
. Then if
![]() $\mathcal {B}_m$
is not dense in
$\mathcal {B}_m$
is not dense in
![]() $\mathcal {U}_{m,d}$
for some
$\mathcal {U}_{m,d}$
for some
![]() $m \geq d+1 \geq r$
,
$m \geq d+1 \geq r$
,
![]() $\operatorname {codim} \mathcal {B}_n \subset \mathcal {U}_{n,d}$
is at least
$\operatorname {codim} \mathcal {B}_n \subset \mathcal {U}_{n,d}$
is at least
![]() $2(m-n)+1$
.
$2(m-n)+1$
.
Proof. First observe that for
![]() $m> d+1$
, the space of lines in any degree d hypersurface in
$m> d+1$
, the space of lines in any degree d hypersurface in
![]() $\mathbb {P}^n$
will sweep out X, so case (3) of Theorem 3.3 cannot occur. We next show that case (2) cannot occur. Let
$\mathbb {P}^n$
will sweep out X, so case (3) of Theorem 3.3 cannot occur. We next show that case (2) cannot occur. Let
![]() $\mathcal {B}_1 \subset \mathcal {U}_{1,d}$
, and let
$\mathcal {B}_1 \subset \mathcal {U}_{1,d}$
, and let
![]() $\mathcal {B}_n \subset \mathcal {U}_{n,d}$
be the tower of induced varieties. It suffices to show
$\mathcal {B}_n \subset \mathcal {U}_{n,d}$
be the tower of induced varieties. It suffices to show
![]() $\mathcal {B}_{d+1}$
is dense in
$\mathcal {B}_{d+1}$
is dense in
![]() $\mathcal {U}_{d+1,d}$
. If a general element of
$\mathcal {U}_{d+1,d}$
. If a general element of
![]() $\mathcal {B}_1$
has at least two distinct points, it follows from [Reference Coskun and RiedlCR] Proposition 4.10(1) that
$\mathcal {B}_1$
has at least two distinct points, it follows from [Reference Coskun and RiedlCR] Proposition 4.10(1) that
![]() $\mathcal {B}_n$
is dense in
$\mathcal {B}_n$
is dense in
![]() $\mathcal {U}_{n,d}$
, which contradicts the hypothesis. Thus, it remains to consider the cases where
$\mathcal {U}_{n,d}$
, which contradicts the hypothesis. Thus, it remains to consider the cases where
![]() $\mathcal {B}_1$
consists of d-fold points and show that the tower of induced varieties is dense in
$\mathcal {B}_1$
consists of d-fold points and show that the tower of induced varieties is dense in
![]() $\mathcal {U}_{m,d}$
. To see this, let
$\mathcal {U}_{m,d}$
. To see this, let
![]() $(p,V(F)) \in \mathcal {U}_{n,d}$
be a general point. Expand the equation of F around p to get
$(p,V(F)) \in \mathcal {U}_{n,d}$
be a general point. Expand the equation of F around p to get
![]() $F = F_1+\cdots F_d$
, where
$F = F_1+\cdots F_d$
, where
![]() $F_i$
is the ith order part of F near p. Then the space of lines in
$F_i$
is the ith order part of F near p. Then the space of lines in
![]() $\mathbb {P}^n$
meeting
$\mathbb {P}^n$
meeting
![]() $V(F)$
to order d near p is
$V(F)$
to order d near p is
![]() $V(F_1,\dots ,F_{d-1})$
. This is nonempty for
$V(F_1,\dots ,F_{d-1})$
. This is nonempty for
![]() $d \leq n-1$
, so the result follows.
$d \leq n-1$
, so the result follows.
Using this result, we can prove a series of results about the nonexistence of rational surfaces in a very general hypersurface X, using our previous work.
Theorem 3.5. Let
![]() $d, n$
and c be integers with
$d, n$
and c be integers with
![]() $d < n+c$
. If a very general hypersurface of degree d in
$d < n+c$
. If a very general hypersurface of degree d in
![]() $\mathbb {P}_{\mathbb {C}}^{n+c}$
is not swept out by rational surfaces from a certain class (e.g., images of generically finite morphisms from Hirzebruch surfaces), then for a very general hypersurface X of degree d in
$\mathbb {P}_{\mathbb {C}}^{n+c}$
is not swept out by rational surfaces from a certain class (e.g., images of generically finite morphisms from Hirzebruch surfaces), then for a very general hypersurface X of degree d in
![]() $\mathbb {P}^n$
, surfaces in this class sweep out a subvariety of X of codimension at least
$\mathbb {P}^n$
, surfaces in this class sweep out a subvariety of X of codimension at least
![]() $2c+1$
. In particular, if
$2c+1$
. In particular, if
![]() $c \geq \frac {n-3}{2}$
, then X contains no surfaces in this class.
$c \geq \frac {n-3}{2}$
, then X contains no surfaces in this class.
Proof. Let
![]() $\mathcal {B}_{n,d}$
be the locus in
$\mathcal {B}_{n,d}$
be the locus in
![]() $\mathcal {U}_{n,d}$
swept out by surfaces in the given class, and let
$\mathcal {U}_{n,d}$
swept out by surfaces in the given class, and let
![]() $\mathcal {B}_{r,d}$
be the tower of induced varieties from
$\mathcal {B}_{r,d}$
be the tower of induced varieties from
![]() $\mathcal {B}_{n,d}$
. Then by assumption, we have that
$\mathcal {B}_{n,d}$
. Then by assumption, we have that
![]() $\mathcal {B}_{n+c,d}$
has codimension at least
$\mathcal {B}_{n+c,d}$
has codimension at least
![]() $1$
in
$1$
in
![]() $\mathcal {U}_{n+c,d}$
. By Corollary 3.4, it follows that
$\mathcal {U}_{n+c,d}$
. By Corollary 3.4, it follows that
![]() $\mathcal {B}_{n,d}$
has codimension at least
$\mathcal {B}_{n,d}$
has codimension at least
![]() $2c+1$
in
$2c+1$
in
![]() $\mathcal {U}_{n,d}$
, and the first part of the result follows. Since generically finite morphisms from a surface to X must sweep out a subvariety of dimension at least 2, we see that X will admit no such morphisms if
$\mathcal {U}_{n,d}$
, and the first part of the result follows. Since generically finite morphisms from a surface to X must sweep out a subvariety of dimension at least 2, we see that X will admit no such morphisms if
![]() $2c+1 \geq n-1-1 = n-2$
. The second result follows.
$2c+1 \geq n-1-1 = n-2$
. The second result follows.
Corollary 3.6. Let
![]() $\alpha $
be a fixed positive number and
$\alpha $
be a fixed positive number and
![]() $\lambda < 1$
another real number with
$\lambda < 1$
another real number with
![]() $\lambda> \frac {3}{2}(2 - \sqrt {2})$
. Then for sufficiently large n, a very general hypersurface of degree
$\lambda> \frac {3}{2}(2 - \sqrt {2})$
. Then for sufficiently large n, a very general hypersurface of degree
![]() $d \geq n\lambda $
contains no images of generically finite morphisms from a rational surface S with
$d \geq n\lambda $
contains no images of generically finite morphisms from a rational surface S with
![]() $H \cdot K \leq \alpha H^2$
on S.
$H \cdot K \leq \alpha H^2$
on S.
Proof. This is a direct application of Theorem 3.5 to the results of Corollary 2.6, replacing
![]() $\lambda $
with
$\lambda $
with
![]() $\frac {2\lambda }{3}$
.
$\frac {2\lambda }{3}$
.
Corollary 3.7. Let S be a rational surface and
![]() $X \subset \mathbb {P}_{\mathbb {C}}^n$
a very general hypersurface of degree greater than
$X \subset \mathbb {P}_{\mathbb {C}}^n$
a very general hypersurface of degree greater than
![]() $(2-\sqrt {2})(n+1)+2$
. Then X is not covered by the images of generically finite morphisms from S.
$(2-\sqrt {2})(n+1)+2$
. Then X is not covered by the images of generically finite morphisms from S.
Proof. Observe that the result is immediate for
![]() $d> n$
, so we may assume
$d> n$
, so we may assume
![]() $d \leq n$
. Let
$d \leq n$
. Let
![]() $p \in S$
be a general point, and let
$p \in S$
be a general point, and let
![]() $\mathcal {B}_{n,d}$
be the locus of images of p under a generically finite morphism
$\mathcal {B}_{n,d}$
be the locus of images of p under a generically finite morphism
![]() $S \to X$
. Let
$S \to X$
. Let
![]() $\mathcal {B}_{n+1,d}$
be part of the tower of induced varieties of
$\mathcal {B}_{n+1,d}$
be part of the tower of induced varieties of
![]() $\mathcal {B}_{n,d}$
. Then by Proposition 3.2,
$\mathcal {B}_{n,d}$
. Then by Proposition 3.2,
![]() $\mathcal {B}_{n+1,d}$
has codimension at least 1 in
$\mathcal {B}_{n+1,d}$
has codimension at least 1 in
![]() $\mathcal {U}_{n+1,d}$
. By Corollary 3.4, it follows that
$\mathcal {U}_{n+1,d}$
. By Corollary 3.4, it follows that
![]() $\mathcal {B}_{n,d}$
has codimension at least 3 in
$\mathcal {B}_{n,d}$
has codimension at least 3 in
![]() $\mathcal {U}_{n,d}$
. Thus, the locus in X swept out by the images of p under generically finite morphisms from S is codimension at least 3 in X. It follows that the images of S under generically finite morphisms sweep out a subvariety of codimension at least 1, as required.
$\mathcal {U}_{n,d}$
. Thus, the locus in X swept out by the images of p under generically finite morphisms from S is codimension at least 3 in X. It follows that the images of S under generically finite morphisms sweep out a subvariety of codimension at least 1, as required.
Corollary 3.8. Let
![]() $\mathcal {S} \to B$
be a family of rational surfaces of dimension
$\mathcal {S} \to B$
be a family of rational surfaces of dimension
![]() $\dim B = k$
and n and d be integers satisfying
$\dim B = k$
and n and d be integers satisfying
![]() $n \geq d> \frac {(2-\sqrt {2})(3n+k+1)}{2} +2$
. Then if
$n \geq d> \frac {(2-\sqrt {2})(3n+k+1)}{2} +2$
. Then if
![]() $X \subset \mathbb {P}_{\mathbb {C}}^n$
is a very general hypersurface of degree d, X admits no generically finite morphisms from any surface in the fibres of
$X \subset \mathbb {P}_{\mathbb {C}}^n$
is a very general hypersurface of degree d, X admits no generically finite morphisms from any surface in the fibres of
![]() $\mathcal {S} \to B$
.
$\mathcal {S} \to B$
.
Note that
![]() $\frac {3(2-\sqrt {2})}{2} < \frac {9}{10}$
, so the result holds for
$\frac {3(2-\sqrt {2})}{2} < \frac {9}{10}$
, so the result holds for
![]() $d \geq \frac {9n}{10}+\frac {3k}{10}+3$
.
$d \geq \frac {9n}{10}+\frac {3k}{10}+3$
.
Proof. As we saw in the proof of Corollary 3.7, for any fixed surface S in the fibres of
![]() $\mathcal {S} \to B$
, we can construct
$\mathcal {S} \to B$
, we can construct
![]() $\mathcal {B}_{r,d}$
, the tower of induced varieties on the locus in
$\mathcal {B}_{r,d}$
, the tower of induced varieties on the locus in
![]() $\mathcal {U}_{n,d}$
swept out by generically finite images from S. We have already seen that
$\mathcal {U}_{n,d}$
swept out by generically finite images from S. We have already seen that
![]() $\mathcal {B}_{m,d}$
has codimension at least
$\mathcal {B}_{m,d}$
has codimension at least
![]() $1$
in
$1$
in
![]() $\mathcal {U}_{m,d}$
for some m satisfying
$\mathcal {U}_{m,d}$
for some m satisfying
![]() $d> (2-\sqrt {2})(m+1)+2$
. Thus,
$d> (2-\sqrt {2})(m+1)+2$
. Thus,
![]() $\mathcal {B}_{m-c,d}$
will have codimension at least
$\mathcal {B}_{m-c,d}$
will have codimension at least
![]() $2c+1$
in
$2c+1$
in
![]() $\mathcal {U}_{m-c,d}$
for r in this range. If we let
$\mathcal {U}_{m-c,d}$
for r in this range. If we let
![]() $\mathcal {B}^{\prime }_{m,d}$
be the union of all the
$\mathcal {B}^{\prime }_{m,d}$
be the union of all the
![]() $\mathcal {B}_{m,d}$
over all the different possible S, then
$\mathcal {B}_{m,d}$
over all the different possible S, then
![]() $\mathcal {B}^{\prime }_{m-c,d}$
will have codimension at least
$\mathcal {B}^{\prime }_{m-c,d}$
will have codimension at least
![]() $2c+1-k$
in
$2c+1-k$
in
![]() $\mathcal {U}_{m-c,d}$
. If
$\mathcal {U}_{m-c,d}$
. If
![]() $2c+1-k \geq m-c$
, then we see that a very general X of degree d in
$2c+1-k \geq m-c$
, then we see that a very general X of degree d in
![]() $\mathbb {P}^{m-c}$
will admit no generically finite maps from the fibres of S. Using
$\mathbb {P}^{m-c}$
will admit no generically finite maps from the fibres of S. Using
![]() $m-c = n$
and rearranging, we see that the result holds as claimed.
$m-c = n$
and rearranging, we see that the result holds as claimed.
Corollary 3.9. If X is a very general hypersurface of degree d in
![]() $\mathbb {P}^n$
and
$\mathbb {P}^n$
and
![]() $n \geq d> \frac {(2-\sqrt {2})(3n+1)}{2}+2$
, then X admits no generically finite maps from Hirzebruch surfaces. In particular, any rational curve in the space of rational curves on X has to meet the boundary.
$n \geq d> \frac {(2-\sqrt {2})(3n+1)}{2}+2$
, then X admits no generically finite maps from Hirzebruch surfaces. In particular, any rational curve in the space of rational curves on X has to meet the boundary.
Acknowledgements
We gratefully acknowledge helpful conversations with Izzet Coskun, Lena Ji, Eric Larson, John Lesieutre and Andrew Putman. We also gratefully acknowledge many helpful comments from the anonymous referee. Roya Beheshti was supported by NSF grant DMS-2101935. Eric Riedl was supported by NSF CAREER grant DMS-1945944.
Conflicts of Interest
None.
Financial support
Roya Beheshti was supported by NSF grant DMS-2101935. Eric Riedl was supported by NSF CAREER grant DMS-1945944.