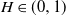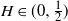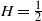1. Introduction
Let
![]() $\{B_H(t),t\in\mathbb{R}_+\}$
, where
$\{B_H(t),t\in\mathbb{R}_+\}$
, where
![]() $\mathbb{R}_+\;:\!=\;[0,\infty)$
, be fractional Brownian motion with Hurst index
$\mathbb{R}_+\;:\!=\;[0,\infty)$
, be fractional Brownian motion with Hurst index
![]() $H\in(0,1)$
(or H-fBm), that is, a centred Gaussian process with the covariance function
$H\in(0,1)$
(or H-fBm), that is, a centred Gaussian process with the covariance function
![]() $\mathbb{C}\text{ov}(B_H(t),B_H(s)) = \frac{1}{2}(s^{2H}+t^{2H}-|t-s|^{2H})$
,
$\mathbb{C}\text{ov}(B_H(t),B_H(s)) = \frac{1}{2}(s^{2H}+t^{2H}-|t-s|^{2H})$
,
![]() $s,t\in\mathbb{R}_+$
. In this manuscript we consider the expected supremum of fractional Brownian motion with drift
$s,t\in\mathbb{R}_+$
. In this manuscript we consider the expected supremum of fractional Brownian motion with drift
![]() $a\in\mathbb{R}$
over time horizon
$a\in\mathbb{R}$
over time horizon
![]() $T>0$
, i.e.
$T>0$
, i.e.
![]() $\mathscr M_H(T,a) \;:\!=\; \mathbb{E}(\!\sup_{t\in[0,T]} B_H(t) - at)$
. Even though the quantity
$\mathscr M_H(T,a) \;:\!=\; \mathbb{E}(\!\sup_{t\in[0,T]} B_H(t) - at)$
. Even though the quantity
![]() $\mathscr M_H(T,a)$
is so fundamental in the theory of extremes of fractional Brownian motion, its value is known explicitly only in two cases:
$\mathscr M_H(T,a)$
is so fundamental in the theory of extremes of fractional Brownian motion, its value is known explicitly only in two cases:
![]() $H=\tfrac{1}{2}$
and
$H=\tfrac{1}{2}$
and
![]() $H=1$
, when
$H=1$
, when
![]() $B_H$
is a standard Brownian motion and a straight line with normally distributed slope, respectively. For general
$B_H$
is a standard Brownian motion and a straight line with normally distributed slope, respectively. For general
![]() $H\in(0,1)$
, the value of
$H\in(0,1)$
, the value of
![]() $\mathscr M_H(T,a)$
could, in principle, be approximated using Monte Carlo methods by simulation of fractional Brownian motion on a dense grid, i.e.
$\mathscr M_H(T,a)$
could, in principle, be approximated using Monte Carlo methods by simulation of fractional Brownian motion on a dense grid, i.e.
![]() $\mathscr M^n_H(T,a) \;:\!=\; \mathbb{E}(\!\sup_{t\in\mathcal T_n} \{B_H(t) - at\})$
, where
$\mathscr M^n_H(T,a) \;:\!=\; \mathbb{E}(\!\sup_{t\in\mathcal T_n} \{B_H(t) - at\})$
, where
![]() $\mathcal T_n \;:\!=\; \{0,{T}/{n},{2T}/{n},\ldots,T\}$
. However, this approach can lead to substantial errors. In [Reference Borovkov, Mishura, Novikov and Zhitlukhin8, Theorem 3.1] it was proven that the absolute error
$\mathcal T_n \;:\!=\; \{0,{T}/{n},{2T}/{n},\ldots,T\}$
. However, this approach can lead to substantial errors. In [Reference Borovkov, Mishura, Novikov and Zhitlukhin8, Theorem 3.1] it was proven that the absolute error
![]() $\mathscr M_H(T,0)-\mathscr M^n_H(T,0)$
behaves roughly (up to logarithmic terms) like
$\mathscr M_H(T,0)-\mathscr M^n_H(T,0)$
behaves roughly (up to logarithmic terms) like
![]() $n^{-H}$
bas
$n^{-H}$
bas
![]() $n\to\infty$
. This becomes problematicbas
$n\to\infty$
. This becomes problematicbas
![]() $H\downarrow0$
, when additionally
$H\downarrow0$
, when additionally
![]() $\mathscr M_H(T,0)\to\infty$
; see also [Reference Makogin17]. Similarly, the error is expected to be large when T is large, since in that case more and more points are needed to cover the interval [0, T]. Surprisingly, even as
$\mathscr M_H(T,0)\to\infty$
; see also [Reference Makogin17]. Similarly, the error is expected to be large when T is large, since in that case more and more points are needed to cover the interval [0, T]. Surprisingly, even as
![]() $H\uparrow 1$
we may also encounter problems because then
$H\uparrow 1$
we may also encounter problems because then
![]() $\mathscr M_H(\infty,a) \to\infty$
for all
$\mathscr M_H(\infty,a) \to\infty$
for all
![]() $a>0$
; see [Reference Bisewski, Dȩbicki and Mandjes4, Reference Malsagov and Mandjes18]. Since the estimation of
$a>0$
; see [Reference Bisewski, Dȩbicki and Mandjes4, Reference Malsagov and Mandjes18]. Since the estimation of
![]() $\mathscr M_H(T,a)$
is so challenging, many works are dedicated to finding its theoretical upper and lower bounds. The most up-to-date bounds for
$\mathscr M_H(T,a)$
is so challenging, many works are dedicated to finding its theoretical upper and lower bounds. The most up-to-date bounds for
![]() $\mathscr M_H(T,0)$
can be found in [Reference Borovkov, Mishura, Novikov and Zhitlukhin8, Reference Borovkov, Mishura, Novikov and Zhitlukhin9]; see also [Reference Shao23, Reference Vardar-Acar and Bulut26] for older results. The most up-to-date bounds for
$\mathscr M_H(T,0)$
can be found in [Reference Borovkov, Mishura, Novikov and Zhitlukhin8, Reference Borovkov, Mishura, Novikov and Zhitlukhin9]; see also [Reference Shao23, Reference Vardar-Acar and Bulut26] for older results. The most up-to-date bounds for
![]() $\mathscr M_H(\infty,a)$
can be found in [Reference Bisewski, Dȩbicki and Mandjes4].
$\mathscr M_H(\infty,a)$
can be found in [Reference Bisewski, Dȩbicki and Mandjes4].
In this work we present a new theoretical lower bound for
![]() $\mathscr M_H(T,a)$
for general
$\mathscr M_H(T,a)$
for general
![]() $T>0$
,
$T>0$
,
![]() $a\in\mathbb{R}$
(including the case
$a\in\mathbb{R}$
(including the case
![]() $T=\infty$
,
$T=\infty$
,
![]() $a>0$
). Our approach is loosely based on recent work [Reference Bisewski, Dȩbicki and Rolski5], where the authors consider a coupling between H-fBms with different values of
$a>0$
). Our approach is loosely based on recent work [Reference Bisewski, Dȩbicki and Rolski5], where the authors consider a coupling between H-fBms with different values of
![]() $H\in(0,1)$
on the Mandelbrot–van Ness field [Reference Mandelbrot and Van Ness19]. By a coupling we mean that H-fBms live in the same probability space and have a non-trivial joint distribution. The idea of considering such a coupling dates back to at least [Reference Benassi, Jaffard and Roux3, Reference Peltier and Véhel20], which introduced a so-called multi-fractional Brownian motion. In this manuscript we consider a coupling provided by the family of linear fractional stable motions with
$H\in(0,1)$
on the Mandelbrot–van Ness field [Reference Mandelbrot and Van Ness19]. By a coupling we mean that H-fBms live in the same probability space and have a non-trivial joint distribution. The idea of considering such a coupling dates back to at least [Reference Benassi, Jaffard and Roux3, Reference Peltier and Véhel20], which introduced a so-called multi-fractional Brownian motion. In this manuscript we consider a coupling provided by the family of linear fractional stable motions with
![]() $\alpha=2$
, see [Reference Samorodnitsky and Taqqu21, Chapter 7.4], which we will call linear fractional Brownian motion. Conceptually, our bound for
$\alpha=2$
, see [Reference Samorodnitsky and Taqqu21, Chapter 7.4], which we will call linear fractional Brownian motion. Conceptually, our bound for
![]() $\mathscr M_H(T,a)$
is very simple: it is defined as the expected value of the H-fBm at the time of the maximum of the corresponding
$\mathscr M_H(T,a)$
is very simple: it is defined as the expected value of the H-fBm at the time of the maximum of the corresponding
![]() $\tfrac{1}{2}$
-fBm (i.e. Brownian motion). The difficult part is the actual calculation of this expected value. This is described in detail in Section 3. Our new lower bound, which we denote by
$\tfrac{1}{2}$
-fBm (i.e. Brownian motion). The difficult part is the actual calculation of this expected value. This is described in detail in Section 3. Our new lower bound, which we denote by
![]() $\underline{\mathscr M}_H(T,a)$
, is introduced in Theorem 1.
$\underline{\mathscr M}_H(T,a)$
, is introduced in Theorem 1.
Our numerical experiments show that
![]() $\underline{\mathscr M}_H(T,a)$
performs exceptionally well in the subdiffusive regime
$\underline{\mathscr M}_H(T,a)$
performs exceptionally well in the subdiffusive regime
![]() $H\in\big(0,\tfrac{1}{2}\big)$
. In fact, the numerical simulations indicate that
$H\in\big(0,\tfrac{1}{2}\big)$
. In fact, the numerical simulations indicate that
![]() $\underline{\mathscr M}_H(T,a)$
gives a better approximation to the ground truth that the Monte Carlo estimates with as many as
$\underline{\mathscr M}_H(T,a)$
gives a better approximation to the ground truth that the Monte Carlo estimates with as many as
![]() $2^{16}$
gridpoints, i.e.
$2^{16}$
gridpoints, i.e.
![]() $\underline{\mathscr M}_H(T,a) \geq \mathscr M^n_H(T,a)$
,
$\underline{\mathscr M}_H(T,a) \geq \mathscr M^n_H(T,a)$
,
![]() $n=2^{16}$
, for all
$n=2^{16}$
, for all
![]() $H\in\big(0,\tfrac{1}{2}\big)$
. We emphasise that
$H\in\big(0,\tfrac{1}{2}\big)$
. We emphasise that
![]() $\underline{\mathscr M}_H(T,a)$
is the theoretical lower bound for
$\underline{\mathscr M}_H(T,a)$
is the theoretical lower bound for
![]() $\mathscr M_H(T,a)$
, which makes the result above even more surprising.
$\mathscr M_H(T,a)$
, which makes the result above even more surprising.
The manuscript is organised as follows. In Section 2 we define linear fractional Brownian motion and establish its Paley–Wiener–Zygmund representation. We also recall the formula for the joint density of the supremum of drifted Brownian motion and its time, and introduce a certain functional of the three-dimensional Bessel bridge, which plays an important role in this manuscript. In Section 3 we show our main results; our lower bound
![]() $\underline{\mathscr M}_H(T,a)$
is presented in Theorem 1 in a general case. Explicit values of
$\underline{\mathscr M}_H(T,a)$
is presented in Theorem 1 in a general case. Explicit values of
![]() $\underline{\mathscr M}_H(T,a)$
are provided in Corollary 2. Additionally, in Theorem 2 we present an explicit formula for the derivative
$\underline{\mathscr M}_H(T,a)$
are provided in Corollary 2. Additionally, in Theorem 2 we present an explicit formula for the derivative
![]() $({\partial}/{\partial H}) \mathscr M_{H}(T,a)\vert_{H=1/2}$
, which was given in terms of a definite integral in [Reference Bisewski, Dȩbicki and Rolski5]. The main results are compared to numerical simulations in Section 4, where the results are also discussed. The proofs of the main results are given in Section 5. In Appendix A we recall the definition and properties of confluent hypergeometric functions. Finally, in Appendix B (available in the Supplementary Material of the online version of this article) we include various calculations needed in the proofs.
$({\partial}/{\partial H}) \mathscr M_{H}(T,a)\vert_{H=1/2}$
, which was given in terms of a definite integral in [Reference Bisewski, Dȩbicki and Rolski5]. The main results are compared to numerical simulations in Section 4, where the results are also discussed. The proofs of the main results are given in Section 5. In Appendix A we recall the definition and properties of confluent hypergeometric functions. Finally, in Appendix B (available in the Supplementary Material of the online version of this article) we include various calculations needed in the proofs.
2. Preliminaries
2.1. Linear fractional Brownian motion
In this section we introduce the definition of linear fractional Brownian motion and establish its Paley–Wiener–Zygmund representation.
Let
![]() $\{B(t)\;:\; t\in\mathbb{R}\}$
be a standard two-sided Brownian motion. For
$\{B(t)\;:\; t\in\mathbb{R}\}$
be a standard two-sided Brownian motion. For
![]() $(H,t)\in(0,1)\times\mathbb{R}_+$
let
$(H,t)\in(0,1)\times\mathbb{R}_+$
let
 \begin{equation} \begin{split} X^+_H(t) & \;:\!=\; \int_{-\infty}^0 \big[(t-s)^{H-({1}/{2})} - (\!-\!s)^{H-({1}/{2})}\big]\,\textrm{d}B(s) + \int_0^t(t-s)^{H-({1}/{2})}\,\textrm{d}B(s), \\[5pt] X^-_H(t) & \;:\!=\; - \int_0^t s^{H-({1}/{2})}\,\textrm{d}B(s) - \int_t^\infty \big[s^{H-({1}/{2})}-(s-t)^{H-({1}/{2})}\big]\,\textrm{d}B(s). \end{split}\end{equation}
\begin{equation} \begin{split} X^+_H(t) & \;:\!=\; \int_{-\infty}^0 \big[(t-s)^{H-({1}/{2})} - (\!-\!s)^{H-({1}/{2})}\big]\,\textrm{d}B(s) + \int_0^t(t-s)^{H-({1}/{2})}\,\textrm{d}B(s), \\[5pt] X^-_H(t) & \;:\!=\; - \int_0^t s^{H-({1}/{2})}\,\textrm{d}B(s) - \int_t^\infty \big[s^{H-({1}/{2})}-(s-t)^{H-({1}/{2})}\big]\,\textrm{d}B(s). \end{split}\end{equation}
Note that in case
![]() $H=\tfrac{1}{2}$
we have
$H=\tfrac{1}{2}$
we have
![]() $X^+_{1/2}(t) = B(t)$
,
$X^+_{1/2}(t) = B(t)$
,
![]() $X^-_{1/2}(t) = -B(t)$
. Furthermore, for
$X^-_{1/2}(t) = -B(t)$
. Furthermore, for
![]() $\boldsymbol{c} \;:\!=\;({c_+},{c_-})\in\mathbb{R}^2_0$
, with
$\boldsymbol{c} \;:\!=\;({c_+},{c_-})\in\mathbb{R}^2_0$
, with
![]() $\mathbb{R}^2_0 \;:\!=\; \mathbb{R}^2\setminus\{(0,0)\}$
, put
$\mathbb{R}^2_0 \;:\!=\; \mathbb{R}^2\setminus\{(0,0)\}$
, put
Finally, for any
![]() $\textbf{c}\in\mathbb{R}_0^2$
, we define the (standardised) linear fractional Brownian motion
$\textbf{c}\in\mathbb{R}_0^2$
, we define the (standardised) linear fractional Brownian motion
![]() $\{B_H^\boldsymbol{c}(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
, where
$\{B_H^\boldsymbol{c}(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
, where
Now, according to [Reference Stoev and Taqqu25, Lemma 4.1] we have
where
We emphasise that
![]() $B_H(t)$
is a Gaussian field with well-known covariance structure, i.e. for each
$B_H(t)$
is a Gaussian field with well-known covariance structure, i.e. for each
![]() $\boldsymbol{c}\in\mathbb{R}^2_0$
, the value of
$\boldsymbol{c}\in\mathbb{R}^2_0$
, the value of
is known, see [Reference Stoev and Taqqu25, Theorem 4.1]. While for each
![]() $H\in(0,1)$
, the process
$H\in(0,1)$
, the process
![]() $\{B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}_+\}$
is an H-fBm (therefore its law is independent of the choice of the pair
$\{B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}_+\}$
is an H-fBm (therefore its law is independent of the choice of the pair
![]() $\boldsymbol{c}$
), the covariance structure (6) of the entire field varies for different
$\boldsymbol{c}$
), the covariance structure (6) of the entire field varies for different
![]() $\boldsymbol{c}$
; see [Reference Stoev and Taqqu25]. In other words, different choices of
$\boldsymbol{c}$
; see [Reference Stoev and Taqqu25]. In other words, different choices of
![]() $\boldsymbol{c}$
will provide different couplings between the fractional Brownian motions. The case
$\boldsymbol{c}$
will provide different couplings between the fractional Brownian motions. The case
![]() $\boldsymbol{c} = (1,0)$
corresponds to the fractional Brownian field introduced by Mandelbrot and van Ness in [Reference Mandelbrot and Van Ness19] (note that in this case we have
$\boldsymbol{c} = (1,0)$
corresponds to the fractional Brownian field introduced by Mandelbrot and van Ness in [Reference Mandelbrot and Van Ness19] (note that in this case we have
![]() $V^\boldsymbol{c}_H = C^2_H$
). We remark that the representation (3) was recently rediscovered in [Reference Kordzakhia, Kutoyants, Novikov and Hin15].
$V^\boldsymbol{c}_H = C^2_H$
). We remark that the representation (3) was recently rediscovered in [Reference Kordzakhia, Kutoyants, Novikov and Hin15].
Following [Reference Bisewski, Dȩbicki and Rolski5], we use the Paley–Wiener–Zygmund (PWZ) representation of processes
![]() $\{\tilde X^+_H(t) \;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
and
$\{\tilde X^+_H(t) \;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
and
![]() $\{\tilde X^-_H(t) \;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
defined in (1),
$\{\tilde X^-_H(t) \;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
defined in (1),
 \begin{equation} \begin{split} \tilde X_H^+(t) & = t^{H-({1}/{2})}\cdot B(t) - \big(H-\tfrac{1}{2}\big) \cdot \int_0^t (t-s)^{H-({3}/{2})} \cdot (B(t)-B(s))\,\textrm{d}s \\[5pt] & \quad + \big(H - \tfrac{1}{2}\big) \cdot \int_{-\infty}^0 [(t-s)^{H-({3}/{2})} - (-s)^{H-({3}/{2})}] \cdot B(s)\,\textrm{d}s, \\[5pt] \tilde X_H^-(t) & = -t^{H-({1}/{2})} \cdot B(t) + \big(H-\tfrac{1}{2}\big) \cdot \int_0^t s^{H-({3}/{2})} \cdot B(s)\,\textrm{d}s \\[5pt] & \quad + (H-({1}/{2})) \cdot \int_t^\infty [s^{H-(3/2)} - (s-t)^{H-(3/2)}] \cdot (B(s)-B(t))\,\textrm{d}s. \end{split}\end{equation}
\begin{equation} \begin{split} \tilde X_H^+(t) & = t^{H-({1}/{2})}\cdot B(t) - \big(H-\tfrac{1}{2}\big) \cdot \int_0^t (t-s)^{H-({3}/{2})} \cdot (B(t)-B(s))\,\textrm{d}s \\[5pt] & \quad + \big(H - \tfrac{1}{2}\big) \cdot \int_{-\infty}^0 [(t-s)^{H-({3}/{2})} - (-s)^{H-({3}/{2})}] \cdot B(s)\,\textrm{d}s, \\[5pt] \tilde X_H^-(t) & = -t^{H-({1}/{2})} \cdot B(t) + \big(H-\tfrac{1}{2}\big) \cdot \int_0^t s^{H-({3}/{2})} \cdot B(s)\,\textrm{d}s \\[5pt] & \quad + (H-({1}/{2})) \cdot \int_t^\infty [s^{H-(3/2)} - (s-t)^{H-(3/2)}] \cdot (B(s)-B(t))\,\textrm{d}s. \end{split}\end{equation}
Proposition 1.
![]() $\{\tilde X^\pm_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
$\{\tilde X^\pm_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
![]() $\{X^\pm_H(t)\;:\;$
$\{X^\pm_H(t)\;:\;$
![]() $(H,t)\in(0,1)\times\mathbb{R}_+\}$
.
$(H,t)\in(0,1)\times\mathbb{R}_+\}$
.
Now let us define the counterpart of the process
![]() $X^\boldsymbol{c}_H(t)$
from (2), i.e., for every
$X^\boldsymbol{c}_H(t)$
from (2), i.e., for every
![]() $\boldsymbol{c}\;:\!=\;({c_+},{c_-})\in\mathbb{R}^2_0$
define the stochastic process
$\boldsymbol{c}\;:\!=\;({c_+},{c_-})\in\mathbb{R}^2_0$
define the stochastic process
![]() $\{\tilde X^\boldsymbol{c}_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
, where
$\{\tilde X^\boldsymbol{c}_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
, where
Corollary 1.
![]() $\{\tilde X^\boldsymbol{c}_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
$\{\tilde X^\boldsymbol{c}_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
![]() $\{X^\boldsymbol{c}_H(t)\;:\;$
$\{X^\boldsymbol{c}_H(t)\;:\;$
![]() $(H,t)\in(0,1)\times\mathbb{R}_+\}$
.
$(H,t)\in(0,1)\times\mathbb{R}_+\}$
.
Corollary 1 generalises [Reference Bisewski, Dȩbicki and Rolski5, Proposition 4.1] in the case
![]() $n=0$
. For completeness, we give a short proof of Proposition 1 below.
$n=0$
. For completeness, we give a short proof of Proposition 1 below.
Proof of Proposition
1. In [Reference Bisewski, Dȩbicki and Rolski5, Proposition 4.1] it was shown that
![]() $\{\tilde X^+_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
$\{\tilde X^+_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
![]() $\{X^+_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
. Showing the sample path continuity of
$\{X^+_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
. Showing the sample path continuity of
![]() $\{\tilde X^-_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is analogous to showing the sample path continuity of
$\{\tilde X^-_H(t)\;:\; (H,t)\in(0,1)\times\mathbb{R}_+\}$
is analogous to showing the sample path continuity of
![]() $\tilde X^+$
, which was done in [Reference Bisewski, Dȩbicki and Rolski5, Proposition 4.2]. Finally, due to [Reference Bisewski, Dȩbicki and Rolski5, Lemma A.1], for any
$\tilde X^+$
, which was done in [Reference Bisewski, Dȩbicki and Rolski5, Proposition 4.2]. Finally, due to [Reference Bisewski, Dȩbicki and Rolski5, Lemma A.1], for any
![]() $(H,t)\in(0,1)\times\mathbb{R}_+$
we have
$(H,t)\in(0,1)\times\mathbb{R}_+$
we have
![]() $\tilde X^-_H(t) = X^-_H(t)$
almost surely (a.s.). This shows that
$\tilde X^-_H(t) = X^-_H(t)$
almost surely (a.s.). This shows that
![]() $\tilde X^-$
is a modification of
$\tilde X^-$
is a modification of
![]() $X^-$
and concludes the proof.
$X^-$
and concludes the proof.
2.2. Joint density of the supremum of drifted Brownian motion and its time
In this section we recall the formulae for the joint density of the supremum of (drifted) Brownian motion over [0, T] and its time due to [Reference Shepp24]. This section relies heavily on [Reference Bisewski, Dȩbicki and Rolski5, Section 2].
Let
![]() $\{B(t)\;:\; t\in\mathbb{R}_+\}$
be a standard Brownian motion. For any
$\{B(t)\;:\; t\in\mathbb{R}_+\}$
be a standard Brownian motion. For any
![]() $T>0$
and
$T>0$
and
![]() $a\in\mathbb{R}$
consider the supremum of drifted Brownian motion and its time, i.e.
$a\in\mathbb{R}$
consider the supremum of drifted Brownian motion and its time, i.e.
and their expected values
In the following, let
![]() $p(t,y;\;T,a)$
be the joint density of
$p(t,y;\;T,a)$
be the joint density of
![]() $(\tau_{1/2}(T,a), M_{1/2}(T,a))$
, i.e.
$(\tau_{1/2}(T,a), M_{1/2}(T,a))$
, i.e.
We note that
![]() $\tau_{1/2}(T,a)$
is well-defined (unique); see the comment below (14). When
$\tau_{1/2}(T,a)$
is well-defined (unique); see the comment below (14). When
![]() $T\in(0,\infty)$
and
$T\in(0,\infty)$
and
![]() $a\in\mathbb{R}$
then
$a\in\mathbb{R}$
then
for
![]() $t\in(0,T)$
and
$t\in(0,T)$
and
![]() $y>0$
. When
$y>0$
. When
![]() $a>0$
, then the pair
$a>0$
, then the pair
![]() $(\tau_{1/2}(\infty,a), M_{1/2}(\infty,a))$
is well-defined, with
$(\tau_{1/2}(\infty,a), M_{1/2}(\infty,a))$
is well-defined, with
for
![]() $t>0$
and
$t>0$
and
![]() $y>0$
.
$y>0$
.
Proposition 2.
-
(i) If
 $T\in(0,\infty)$
and
$T\in(0,\infty)$
and
 $a\neq 0$
then
$a\neq 0$
then
 \begin{align*} \mathscr M_{1/2}(T,a) & = \frac{1}{2a}\bigg({-}a^2T + (1+ a^2T)\textrm{erf}\bigg(a\sqrt{\frac{T}{2}}\bigg) + \sqrt{\frac{2T}{\pi}}\cdot a\textrm{e}^{-a^2T/2}\bigg), \\[5pt] \mathcal E_{1/2}(T,a) & = \frac{1}{2a^2}\bigg(a^2T + (1-a^2T)\textrm{erf}\bigg(a\sqrt{\frac{T}{2}}\bigg) - \sqrt{\frac{2T}{\pi}}\cdot a\textrm{e}^{-a^2T/2}\bigg); \end{align*}
\begin{align*} \mathscr M_{1/2}(T,a) & = \frac{1}{2a}\bigg({-}a^2T + (1+ a^2T)\textrm{erf}\bigg(a\sqrt{\frac{T}{2}}\bigg) + \sqrt{\frac{2T}{\pi}}\cdot a\textrm{e}^{-a^2T/2}\bigg), \\[5pt] \mathcal E_{1/2}(T,a) & = \frac{1}{2a^2}\bigg(a^2T + (1-a^2T)\textrm{erf}\bigg(a\sqrt{\frac{T}{2}}\bigg) - \sqrt{\frac{2T}{\pi}}\cdot a\textrm{e}^{-a^2T/2}\bigg); \end{align*}
-
(ii) if
 $a>0$
then
$a>0$
then
 $\mathscr M_{1/2}(\infty,a) = {1}/{2a}$
and
$\mathscr M_{1/2}(\infty,a) = {1}/{2a}$
and
 $\mathcal E_{1/2}(\infty,a) = {1}/{2a^2}$
;
$\mathcal E_{1/2}(\infty,a) = {1}/{2a^2}$
; -
(iii) if
 $T\in(0,\infty)$
then
$T\in(0,\infty)$
then
 $\mathscr M_{1/2}(T,0) = \sqrt{{2T}/{\pi}}$
and
$\mathscr M_{1/2}(T,0) = \sqrt{{2T}/{\pi}}$
and
 $\mathcal E_{1/2}(T,0) = {T}/{2}$
.
$\mathcal E_{1/2}(T,0) = {T}/{2}$
.
Proof. The fomula for
![]() $\mathscr M_{1/2}(T,a)$
can be obtained from the Laplace transform of
$\mathscr M_{1/2}(T,a)$
can be obtained from the Laplace transform of
![]() $M_{1/2}(T,a)$
; see [Reference Borodin and Salminen7, (1.1.1.3) and (2.1.1.3)]. The formula for
$M_{1/2}(T,a)$
; see [Reference Borodin and Salminen7, (1.1.1.3) and (2.1.1.3)]. The formula for
![]() $\mathcal E_{1/2}(T,a)$
could similarly be obtained from the Laplace transform of
$\mathcal E_{1/2}(T,a)$
could similarly be obtained from the Laplace transform of
![]() $\tau_{1/2}(T,a)$
. However, numerical calculations indicate that the formulas for the Laplace transforms (1.1.12.3) and (2.1.12.3) in [Reference Borodin and Salminen7] are incorrect. Therefore, we provide our own derivation of
$\tau_{1/2}(T,a)$
. However, numerical calculations indicate that the formulas for the Laplace transforms (1.1.12.3) and (2.1.12.3) in [Reference Borodin and Salminen7] are incorrect. Therefore, we provide our own derivation of
![]() $\mathcal E_{1/2}(T,a)$
in Appendix B (available in the Supplementary Material of the online version of this manuscript).
$\mathcal E_{1/2}(T,a)$
in Appendix B (available in the Supplementary Material of the online version of this manuscript).
Finally, we introduce a certain functional of Brownian motion, which plays an important role in this manuscript. We note that its special case
![]() $\big(H = \tfrac{1}{2}\big)$
appeared in [Reference Bisewski, Dȩbicki and Rolski5, (2.8)]. In what follows let
$\big(H = \tfrac{1}{2}\big)$
appeared in [Reference Bisewski, Dȩbicki and Rolski5, (2.8)]. In what follows let
![]() $Y(t) \;:\!=\; B(t)-at$
and
$Y(t) \;:\!=\; B(t)-at$
and
Following [Reference Bisewski, Dȩbicki and Rolski5], we recognise that the conditional distribution of the process
![]() $\{Y(t)-Y(t-s)\;:\; s\in[0,t]\}$
given
$\{Y(t)-Y(t-s)\;:\; s\in[0,t]\}$
given
![]() $(\tau_{1/2}(T,a),M_{1/2}(T,a)) = (t,y)$
follows the law of the generalised three-dimensional Bessel bridge from (0,0) to (t, y). Therefore,
$(\tau_{1/2}(T,a),M_{1/2}(T,a)) = (t,y)$
follows the law of the generalised three-dimensional Bessel bridge from (0,0) to (t, y). Therefore,
![]() $I_H(t,y)$
can be thought of as an expected value of a certain ‘Brownian area’; see [Reference Janson14] for a survey on Brownian areas. It turns out that the function
$I_H(t,y)$
can be thought of as an expected value of a certain ‘Brownian area’; see [Reference Janson14] for a survey on Brownian areas. It turns out that the function
![]() $I_H(t,y)$
can be explicitly calculated. In the following, U(a, b, z) is Tricomi’s confluent hypergeometric function; see (23) in Appendix A.
$I_H(t,y)$
can be explicitly calculated. In the following, U(a, b, z) is Tricomi’s confluent hypergeometric function; see (23) in Appendix A.
Lemma 1.
If
![]() $H\in\big(0,\tfrac{1}{2}\big)\cup\big(\tfrac{1}{2},1\big)$
and
$H\in\big(0,\tfrac{1}{2}\big)\cup\big(\tfrac{1}{2},1\big)$
and
![]() $t,y>0$
, then
$t,y>0$
, then
Proof of Lemma 1. Let
From [Reference Bisewski, Dȩbicki and Rolski5, (2.7)] we have
for
![]() $x>0$
. Using the Fubini–Tonelli theorem we have
$x>0$
. Using the Fubini–Tonelli theorem we have
The rest of the proof is purely calculational. For completeness, it is given in Appendix B (available in the Supplementary Material of the online version of this manuscript).
3. Main results
Let
![]() $\{B(t) \;:\; t\in\mathbb{R}\}$
be a standard, two-sided Brownian motion. Consider the PWZ representation of linear fractional Brownian motion with parameter
$\{B(t) \;:\; t\in\mathbb{R}\}$
be a standard, two-sided Brownian motion. Consider the PWZ representation of linear fractional Brownian motion with parameter
![]() $\boldsymbol{c}\in\mathbb{R}^2_0$
, i.e.
$\boldsymbol{c}\in\mathbb{R}^2_0$
, i.e.
![]() $\{\tilde B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}^+\}$
, where
$\{\tilde B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}^+\}$
, where
with
![]() $\tilde X^\boldsymbol{c}_H(t)$
defined in (8) and
$\tilde X^\boldsymbol{c}_H(t)$
defined in (8) and
![]() $V^\boldsymbol{c}_H$
defined in (4). Then, according to Corollary 1,
$V^\boldsymbol{c}_H$
defined in (4). Then, according to Corollary 1,
![]() $\{\tilde B^\boldsymbol{c}_H(t)\;:\; H\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
$\{\tilde B^\boldsymbol{c}_H(t)\;:\; H\in(0,1)\times\mathbb{R}_+\}$
is a continuous modification of
![]() $\{B^\boldsymbol{c}_H(t)\;:\; H\in(0,1)\times\mathbb{R}_+\}$
and therefore, for each fixed H,
$\{B^\boldsymbol{c}_H(t)\;:\; H\in(0,1)\times\mathbb{R}_+\}$
and therefore, for each fixed H,
![]() $\{\tilde B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}_+\}$
is a fractional Brownian motion with Hurst index H. We note that all the processes
$\{\tilde B^\boldsymbol{c}_H(t)\;:\; t\in\mathbb{R}_+\}$
is a fractional Brownian motion with Hurst index H. We note that all the processes
![]() $\tilde B^\boldsymbol{c}_H$
live in the same probability space and are, in fact, defined pathwise for every realisation of the driving Brownian motion.
$\tilde B^\boldsymbol{c}_H$
live in the same probability space and are, in fact, defined pathwise for every realisation of the driving Brownian motion.
For each
![]() $\boldsymbol{c}\in\mathbb{R}^2_0$
,
$\boldsymbol{c}\in\mathbb{R}^2_0$
,
![]() $a\in\mathbb{R}$
, and
$a\in\mathbb{R}$
, and
![]() $T>0$
define
$T>0$
define
which is the supremum of the drifted fractional Brownian motion with parameter
![]() $\boldsymbol{c}$
and its location. We note that
$\boldsymbol{c}$
and its location. We note that
![]() $\tau^\boldsymbol{c}_H(T,a)$
is well-defined (almost surely unique); see [Reference Ferger12]. Now we define the expected values of the supremum,
$\tau^\boldsymbol{c}_H(T,a)$
is well-defined (almost surely unique); see [Reference Ferger12]. Now we define the expected values of the supremum,
Recall that in the case
![]() $\boldsymbol{c}=(1,0)$
and
$\boldsymbol{c}=(1,0)$
and
![]() $H=\tfrac{1}{2}$
, the random variables and their expectations were already defined in (9) and (10). Notice how
$H=\tfrac{1}{2}$
, the random variables and their expectations were already defined in (9) and (10). Notice how
![]() $\mathscr M_H(T,a)$
does not depend on
$\mathscr M_H(T,a)$
does not depend on
![]() $\boldsymbol{c}$
, because as
$\boldsymbol{c}$
, because as
![]() $\boldsymbol{c}$
varies, the law of the supremum does not change.
$\boldsymbol{c}$
varies, the law of the supremum does not change.
3.1. The lower bound
We now proceed to derive the lower bound for
![]() $\mathscr M_H(T,a)$
. The final result is provided in Theorem 1 at the end of this subsection. All proofs are provided in Section 5.
$\mathscr M_H(T,a)$
. The final result is provided in Theorem 1 at the end of this subsection. All proofs are provided in Section 5.
For each
![]() $\boldsymbol{c}\in\mathbb{R}^2_0$
define
$\boldsymbol{c}\in\mathbb{R}^2_0$
define
which, in words, is the expected value of the drifted fractional Brownian motion with parameter
![]() $\boldsymbol{c}$
evaluated at the time of the supremum of the driving Brownian motion
$\boldsymbol{c}$
evaluated at the time of the supremum of the driving Brownian motion
![]() $\tau_{1/2}(T,a)$
defined in (9). Clearly, this yields a lower bound for the expected supremum, i.e.
$\tau_{1/2}(T,a)$
defined in (9). Clearly, this yields a lower bound for the expected supremum, i.e.
![]() $\mathscr M_H(T,a) \geq m^\boldsymbol{c}_H(T,a)$
. We can further maximise our lower bound by taking the supremum over all
$\mathscr M_H(T,a) \geq m^\boldsymbol{c}_H(T,a)$
. We can further maximise our lower bound by taking the supremum over all
![]() $\boldsymbol{c}\in\mathbb{R}^2_0$
and define
$\boldsymbol{c}\in\mathbb{R}^2_0$
and define
![]() $m_H(T,a) \;:\!=\; \sup_{\boldsymbol{c}\in\mathbb{R}^2_0} m^\boldsymbol{c}_H(T,a)$
. It turns out that the value of
$m_H(T,a) \;:\!=\; \sup_{\boldsymbol{c}\in\mathbb{R}^2_0} m^\boldsymbol{c}_H(T,a)$
. It turns out that the value of
![]() $m_H(T,a)$
can be found explicitly. Before showing that formula in Proposition 4, we define the useful functionals
$m_H(T,a)$
can be found explicitly. Before showing that formula in Proposition 4, we define the useful functionals
Lemma 2.
If
![]() $T\in(0,\infty)$
and
$T\in(0,\infty)$
and
![]() $a\in\mathbb{R}$
then
$a\in\mathbb{R}$
then
![]() $\mathcal J^-_H(T,a) = -\mathcal J_H(T,-a).$
$\mathcal J^-_H(T,a) = -\mathcal J_H(T,-a).$
The proof of Lemma 2 is given in Section 5. In the following,
![]() $\gamma(\alpha,z)$
is the incomplete Gamma function; see (31) in Appendix A.
$\gamma(\alpha,z)$
is the incomplete Gamma function; see (31) in Appendix A.
Proposition 3.
 \begin{equation*} \mathcal J_H(T,a) = \begin{cases} \frac{2^{H}}{\sqrt{2\pi}\big(H+\tfrac{1}{2}\big)} \cdot |a|^{-2H}\gamma(H,{a^2T}/{2}), & a\neq 0,\ T\in(0,\infty); \\[12pt] \frac{2^{H}\Gamma(H)}{\sqrt{2\pi}\big(H+\tfrac{1}{2}\big)} \cdot |a|^{-2H}, & a > 0, \ T=\infty; \\[12pt] \frac{T^{H}}{\sqrt{2\pi}H\big(H+\tfrac{1}{2}\big)}, & a=0, \ T\in(0,\infty). \end{cases} \end{equation*}
\begin{equation*} \mathcal J_H(T,a) = \begin{cases} \frac{2^{H}}{\sqrt{2\pi}\big(H+\tfrac{1}{2}\big)} \cdot |a|^{-2H}\gamma(H,{a^2T}/{2}), & a\neq 0,\ T\in(0,\infty); \\[12pt] \frac{2^{H}\Gamma(H)}{\sqrt{2\pi}\big(H+\tfrac{1}{2}\big)} \cdot |a|^{-2H}, & a > 0, \ T=\infty; \\[12pt] \frac{T^{H}}{\sqrt{2\pi}H\big(H+\tfrac{1}{2}\big)}, & a=0, \ T\in(0,\infty). \end{cases} \end{equation*}
Finally, we can show the following.
Proposition 4.
If
![]() $a\in\mathbb{R}$
and
$a\in\mathbb{R}$
and
![]() $T\in(0,\infty)$
or
$T\in(0,\infty)$
or
![]() $a>0$
and
$a>0$
and
![]() $T=\infty$
, then
$T=\infty$
, then
and
with
![]() $V^\boldsymbol{c}_H$
and
$V^\boldsymbol{c}_H$
and
![]() $C_H$
defined in (4) and (5), respectively.
$C_H$
defined in (4) and (5), respectively.
We emphasise that the values of
![]() $\mathcal E_{1/2}(T,a)$
and
$\mathcal E_{1/2}(T,a)$
and
![]() $\mathcal J_H(T,a)$
are known; see Propositions 2 and 3 respectively.
$\mathcal J_H(T,a)$
are known; see Propositions 2 and 3 respectively.
We can further improve the lower bound derived in Proposition 4 simply by using the self-similarity of fractional Brownian motion. For any
![]() $\rho>0$
we have
$\rho>0$
we have
![]() $\mathscr M_H(T,a) = \rho^{-H}\mathscr M_H(\rho T,\rho^{H-1}a)$
, which also holds for
$\mathscr M_H(T,a) = \rho^{-H}\mathscr M_H(\rho T,\rho^{H-1}a)$
, which also holds for
![]() $a>0$
and
$a>0$
and
![]() $T=\infty$
, i.e.
$T=\infty$
, i.e.
![]() $\mathscr M_H(\infty,a) = \rho^{-H}\mathscr M_H(\infty,\rho^{H-1}a)$
.
$\mathscr M_H(\infty,a) = \rho^{-H}\mathscr M_H(\infty,\rho^{H-1}a)$
.
Finally, let
Theorem 1.
For any
![]() $H\in(0,1)$
,
$H\in(0,1)$
,
![]() $T>0$
, and
$T>0$
, and
![]() $a\in\mathbb{R}$
,
$a\in\mathbb{R}$
,
![]() $\mathscr M_H(T,a) \geq \underline{\mathscr M}_H(T,a)$
.
$\mathscr M_H(T,a) \geq \underline{\mathscr M}_H(T,a)$
.
For general (T, a), the solution to the optimisation problem (18) can be found numerically. We were able to determine the value of
![]() $\underline{\mathscr M}_H(T,a)$
explicitly in two special cases, which we display in the following corollary. For convenience, we also provide the corresponding values of
$\underline{\mathscr M}_H(T,a)$
explicitly in two special cases, which we display in the following corollary. For convenience, we also provide the corresponding values of
![]() $m_H(T,a)$
.
$m_H(T,a)$
.
Corollary 2.
For
![]() $H\in(0,1)$
, with
$H\in(0,1)$
, with
![]() $C_H$
defined in (5),
$C_H$
defined in (5),
-
(i) if
 $T\in(0,\infty)$
, then
$T\in(0,\infty)$
, then
 \begin{align*}\displaystyle \underline{\mathscr M}_H(T,0) = m_H(T,0) = \frac{T^H}{\sqrt{2\pi}\,C_HH\big(H+\tfrac{1}{2}\big) \sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)};\end{align*}
\begin{align*}\displaystyle \underline{\mathscr M}_H(T,0) = m_H(T,0) = \frac{T^H}{\sqrt{2\pi}\,C_HH\big(H+\tfrac{1}{2}\big) \sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)};\end{align*}
-
(ii) if
 $a>0$
, then
$a>0$
, then
 \begin{align*} \underline{\mathscr M}_H(\infty,a) & = \frac{1-H}{2aH} \bigg(\frac{2^{H+1}a^{1-2H}H\Gamma(H)}{\sqrt{2\pi}C_H\big(H+\tfrac{1}{2}\big)\sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)}\bigg)^{1/(1-H)}, \\[5pt] m_H(\infty,a) & = \frac{2^{H}\Gamma(H)}{\sqrt{2\pi}C_Ha^{2H}\big(H+\tfrac{1}{2}\big) \sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)} - \frac{1}{2a}. \end{align*}
\begin{align*} \underline{\mathscr M}_H(\infty,a) & = \frac{1-H}{2aH} \bigg(\frac{2^{H+1}a^{1-2H}H\Gamma(H)}{\sqrt{2\pi}C_H\big(H+\tfrac{1}{2}\big)\sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)}\bigg)^{1/(1-H)}, \\[5pt] m_H(\infty,a) & = \frac{2^{H}\Gamma(H)}{\sqrt{2\pi}C_Ha^{2H}\big(H+\tfrac{1}{2}\big) \sin\big(\tfrac12{\pi}\big(H+\tfrac{1}{2}\big)\big)} - \frac{1}{2a}. \end{align*}
The proof of Corollary 2 relies solely on simple algebraic manipulations.
3.2. Secondary results
Before ending this section, we would like to present two immediate corollaries that are implied by our main results. The first result describes the asymptotic behavior of
![]() $\mathscr M_H(T,0)$
as
$\mathscr M_H(T,0)$
as
![]() $H\downarrow0$
, while the second result pertains to the evaluation of the derivative of the expected supremum
$H\downarrow0$
, while the second result pertains to the evaluation of the derivative of the expected supremum
![]() $\mathscr M_H(T,a)$
at
$\mathscr M_H(T,a)$
at
![]() $H=\tfrac{1}{2}$
.
$H=\tfrac{1}{2}$
.
3.2.1. Behavior of
 $\underline{\mathscr{M}}_H(1,0)$
as
$\underline{\mathscr{M}}_H(1,0)$
as
 $\textit{H}\downarrow 0$
$\textit{H}\downarrow 0$
Using the formula for
![]() $\underline{\mathscr{M}}_H(T,0)$
from Theorem 1(i), it is easy to obtain the following result.
$\underline{\mathscr{M}}_H(T,0)$
from Theorem 1(i), it is easy to obtain the following result.
Corollary 3.
The asymptotic lower bound in Corollary 3 is over five times larger than the corresponding bound derived in [Reference Borovkov, Mishura, Novikov and Zhitlukhin8, Theorem 2.1(i)], where it was shown that
![]() $\mathscr M_H(1,0) \geq (4H\pi \textrm{e}\log(2))^{-1/2}$
for all
$\mathscr M_H(1,0) \geq (4H\pi \textrm{e}\log(2))^{-1/2}$
for all
![]() $H\in(0,1)$
. Moreover, together with [Reference Borovkov, Mishura, Novikov and Zhitlukhin9, Corollary 2], our result implies that
$H\in(0,1)$
. Moreover, together with [Reference Borovkov, Mishura, Novikov and Zhitlukhin9, Corollary 2], our result implies that
![]() $1.128 \leq H^{-1/2}\mathscr M_H(1,0) \leq 1.695$
for all H small enough. Determining whether the limit
$1.128 \leq H^{-1/2}\mathscr M_H(1,0) \leq 1.695$
for all H small enough. Determining whether the limit
![]() $H^{-1/2}\mathscr M_H(1,0)$
as
$H^{-1/2}\mathscr M_H(1,0)$
as
![]() $H\to0$
exists and finding its value remain interesting open questions.
$H\to0$
exists and finding its value remain interesting open questions.
3.2.2. Derivative of the expected supremum
Recently, [Reference Bisewski, Dȩbicki and Rolski5] considered the derivative of the expected supremum with respect to the Hurst parameter at
![]() $H=\tfrac{1}{2}$
, that is
$H=\tfrac{1}{2}$
, that is
![]() $\mathscr{M}'_{\!\!1/2}(T,a) \;:\!=\; ({\partial}/{\partial H})\mathscr M_H(T,a)\big|_{H={1}/{2}}$
. In [Reference Bisewski, Dȩbicki and Rolski5, Theorem 3.1], they derived an expression for
$\mathscr{M}'_{\!\!1/2}(T,a) \;:\!=\; ({\partial}/{\partial H})\mathscr M_H(T,a)\big|_{H={1}/{2}}$
. In [Reference Bisewski, Dȩbicki and Rolski5, Theorem 3.1], they derived an expression for
![]() $\mathscr{M}'_{\!\!1/2}(T,a)$
in terms of a definite double integral and in [Reference Bisewski, Dȩbicki and Rolski5, Corollary 3.3] they derived a more explicit result in two special cases
$\mathscr{M}'_{\!\!1/2}(T,a)$
in terms of a definite double integral and in [Reference Bisewski, Dȩbicki and Rolski5, Corollary 3.3] they derived a more explicit result in two special cases
![]() $a=0$
and
$a=0$
and
![]() $T=\infty$
. Using the formula for
$T=\infty$
. Using the formula for
![]() $\mathcal J_H(T,a)$
we established in Proposition 3, we are able to explicitly evaluate the derivative in the general case. In the following, let
$\mathcal J_H(T,a)$
we established in Proposition 3, we are able to explicitly evaluate the derivative in the general case. In the following, let
![]() $\gamma'(s,x) = ({\partial}/{\partial s})\gamma(s,x)$
.
$\gamma'(s,x) = ({\partial}/{\partial s})\gamma(s,x)$
.
Theorem 2.
Note that the continuous extension of the function
![]() $\mathscr{M}'_{\!\!1/2}(T,a)$
to (T,0) and
$\mathscr{M}'_{\!\!1/2}(T,a)$
to (T,0) and
![]() $(\infty,a)$
agrees with [Reference Bisewski, Dȩbicki and Rolski5, Corollary 3.3].
$(\infty,a)$
agrees with [Reference Bisewski, Dȩbicki and Rolski5, Corollary 3.3].
Proof of Theorem 2. The proof of [Reference Bisewski, Dȩbicki and Rolski5, Theorem 3.1] implies that
Therefore, using the formula for
![]() $m^{(1,0)}_H(T,a)$
from Proposition 4, we find that
$m^{(1,0)}_H(T,a)$
from Proposition 4, we find that
![]() $\mathscr{M}'_{\!\!1/2}(T,a) = \mathcal J_{1/2}(T,a) + ({\partial}/{\partial H})\mathcal J_H(T,a)\vert_{H=1/2}$
. The proof is concluded after simple algebraic manipulations.
$\mathscr{M}'_{\!\!1/2}(T,a) = \mathcal J_{1/2}(T,a) + ({\partial}/{\partial H})\mathcal J_H(T,a)\vert_{H=1/2}$
. The proof is concluded after simple algebraic manipulations.
4. Numerical experiments
In this section we compare our theoretical lower bound
![]() $\underline{\mathscr M}_H(T,a)$
with Monte Carlo simulations.
$\underline{\mathscr M}_H(T,a)$
with Monte Carlo simulations.
In our experiments we use the circulant embedding method (also called the Davies–Harte method [Reference Davies and Harte10]) for simulating fractional Brownian motion; see also [Reference Dieker11] for various methods of simulation. Experiments were performed in Python, and the code for the Davies–Harte method was adapted from [Reference Kroese and Botev16, Section 12.4.2]. The method relies on the simulation of fractional Brownian motion on an equidistant grid of n points, i.e.
![]() $(B(0), B({T}/{n}), B({2T}/{n}), \ldots, B(T))$
. The resulting estimator has the expected value
$(B(0), B({T}/{n}), B({2T}/{n}), \ldots, B(T))$
. The resulting estimator has the expected value
![]() $\mathscr M^n_H(T,a) \;:\!=\; \mathbb{E}\big(\!\sup_{t\in\mathcal T_n} \{B_H(t) - at\}\big)$
, where
$\mathscr M^n_H(T,a) \;:\!=\; \mathbb{E}\big(\!\sup_{t\in\mathcal T_n} \{B_H(t) - at\}\big)$
, where
![]() $\mathcal T_n \;:\!=\; \{0,{T}/{n},{2T}/{n},\ldots,T\}$
. Clearly,
$\mathcal T_n \;:\!=\; \{0,{T}/{n},{2T}/{n},\ldots,T\}$
. Clearly,
![]() $\mathscr M^n_H(T,a) \leq \mathscr M_H(T,a)$
; i.e., on average, the Monte Carlo estimator underestimates the ground truth, as the supremum is taken over a finite subset of [0, T]. Nonetheless, as
$\mathscr M^n_H(T,a) \leq \mathscr M_H(T,a)$
; i.e., on average, the Monte Carlo estimator underestimates the ground truth, as the supremum is taken over a finite subset of [0, T]. Nonetheless, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $\mathscr M^n_H(T,a) \to \mathscr M_H(T,a)$
.
$\mathscr M^n_H(T,a) \to \mathscr M_H(T,a)$
.
In our experiments, we consider three different cases: (i)
![]() $T=1$
,
$T=1$
,
![]() $a=0$
; (ii)
$a=0$
; (ii)
![]() $T=1$
,
$T=1$
,
![]() $a=1$
; and, finally, (iii)
$a=1$
; and, finally, (iii)
![]() $T=\infty$
,
$T=\infty$
,
![]() $a=1$
. In each case the theoretical lower bound
$a=1$
. In each case the theoretical lower bound
![]() $\underline{\mathscr M}_H(T,a)$
is compared with the corresponding simulation results
$\underline{\mathscr M}_H(T,a)$
is compared with the corresponding simulation results
![]() $\widehat{\mathscr M}^n_H(T,a)$
for
$\widehat{\mathscr M}^n_H(T,a)$
for
![]() $n\in\{2^{10},2^{12},2^{14},2^{16}\}$
based on
$n\in\{2^{10},2^{12},2^{14},2^{16}\}$
based on
![]() $20\,000$
independent runs of the Davies–Harte algorithm; in case (ii) we took
$20\,000$
independent runs of the Davies–Harte algorithm; in case (ii) we took
![]() $T=10$
because it is not possible to simulate the process over the infinite time horizon.
$T=10$
because it is not possible to simulate the process over the infinite time horizon.
The results corresponding to cases (i)–(iii) are displayed in Figs. 1–3. Each curve is surrounded by its 95% confidence interval depicted as a shaded blue area. The results are presented in two different scales. We interpret the results on the figures on the left and on the right separately, in the following two paragraphs.

Figure 1. Numerical results for the case
![]() $T=1, a=0$
.
$T=1, a=0$
.

Figure 2. Numerical results for the case
![]() $T=1, a=1$
.
$T=1, a=1$
.

Figure 3. Numerical results for the case
![]() $T=\infty, a=1$
.
$T=\infty, a=1$
.
In the figures on the left, we compare the bound with the simulation results on the ‘high’ level for all
![]() $H\in(0.01,1)$
. The blue dots at
$H\in(0.01,1)$
. The blue dots at
![]() $H=\tfrac{1}{2}$
and
$H=\tfrac{1}{2}$
and
![]() $H=1$
correspond to the known values of
$H=1$
correspond to the known values of
![]() $\mathscr M_{1/2}(T,a)$
and
$\mathscr M_{1/2}(T,a)$
and
![]() $\mathscr M_{1}(T,a)$
respectively; the value at
$\mathscr M_{1}(T,a)$
respectively; the value at
![]() $H=1$
in Fig. 3 is not shown because
$H=1$
in Fig. 3 is not shown because
![]() $\mathscr M_1(\infty,1) = \infty$
. As expected, the value of
$\mathscr M_1(\infty,1) = \infty$
. As expected, the value of
![]() $\widehat{\mathscr M}_H^n(T,a)$
is increasing, as n is increasing. The simulation results seem to roughly agree with the ground truth at
$\widehat{\mathscr M}_H^n(T,a)$
is increasing, as n is increasing. The simulation results seem to roughly agree with the ground truth at
![]() $H=\tfrac{1}{2}$
and
$H=\tfrac{1}{2}$
and
![]() $H=1$
, while the lower bound agrees with the ground truth at
$H=1$
, while the lower bound agrees with the ground truth at
![]() $H=\tfrac{1}{2}$
by definition, i.e.
$H=\tfrac{1}{2}$
by definition, i.e.
![]() $\underline{\mathscr M}_{1/2}(T,a) = \mathscr M_{1/2}(T,a)$
. On the ‘high’ level, we can conclude that the lower bound
$\underline{\mathscr M}_{1/2}(T,a) = \mathscr M_{1/2}(T,a)$
. On the ‘high’ level, we can conclude that the lower bound
![]() $\underline{\mathscr M}_H(T,a)$
$\underline{\mathscr M}_H(T,a)$
-
is close to the simulation results for all
 $H\approx \tfrac{1}{2}$
;
$H\approx \tfrac{1}{2}$
; -
perfoms much better than the simulation results as
 $H\to0$
; and
$H\to0$
; and -
performs worse when
 $H\to1$
(in fact, the bound seems to converge to 0 there).
$H\to1$
(in fact, the bound seems to converge to 0 there).
On the right of the figures, we compare the bound with the simulation results in the region
![]() $H\in(0.2,0.8)$
. We show the relative error between the theoretical lower bound and the simulation results based on
$H\in(0.2,0.8)$
. We show the relative error between the theoretical lower bound and the simulation results based on
![]() $n=2^{16}$
grid points, i.e.
$n=2^{16}$
grid points, i.e.
![]() $(\underline{\mathscr M}_H(T,a)-\widehat{\mathscr M}_H^n(T,a))/\widehat{\mathscr M}_H^n(T,a)$
. We note that if the relative error is positive, then the theoretical lower bound yields a better approximation to the ground truth than the Monte Carlo method, which is indicated by the green area below the curve on the plot. In this sense, we see that the theoretical lower bound outperforms the Monte Carlo simulations for
$(\underline{\mathscr M}_H(T,a)-\widehat{\mathscr M}_H^n(T,a))/\widehat{\mathscr M}_H^n(T,a)$
. We note that if the relative error is positive, then the theoretical lower bound yields a better approximation to the ground truth than the Monte Carlo method, which is indicated by the green area below the curve on the plot. In this sense, we see that the theoretical lower bound outperforms the Monte Carlo simulations for
![]() $H\in\big(0,\tfrac{1}{2}\big)$
in all three cases (i)–(iii). We remark that the value of the relative error at
$H\in\big(0,\tfrac{1}{2}\big)$
in all three cases (i)–(iii). We remark that the value of the relative error at
![]() $H=\tfrac{1}{2}$
approximately equals
$H=\tfrac{1}{2}$
approximately equals
![]() $0.5\%$
in Fig. 1 and
$0.5\%$
in Fig. 1 and
![]() $0.7\%$
in Fig. 2; this roughly agrees with [Reference Bisewski and Ivanovs6, Corollary 4.3], which states that
$0.7\%$
in Fig. 2; this roughly agrees with [Reference Bisewski and Ivanovs6, Corollary 4.3], which states that
where
![]() $\zeta(\!\cdot\!)$
is the Riemann zeta function. See also [Reference Asmussen, Glynn and Pitman2, Theorem 2] for the case
$\zeta(\!\cdot\!)$
is the Riemann zeta function. See also [Reference Asmussen, Glynn and Pitman2, Theorem 2] for the case
![]() $a=0$
.
$a=0$
.
5. Proofs
Here we provide proofs of Lemma 2, Proposition 3, and Proposition 4 from Section 3.1.
Proof of Lemma
2. For brevity we write
![]() $\tau\;:\!=\;\tau_{1/2}(T,a)$
and put
$\tau\;:\!=\;\tau_{1/2}(T,a)$
and put
![]() $Y(t)\;:\!=\;B(t)-at$
. According to the PWZ representation of
$Y(t)\;:\!=\;B(t)-at$
. According to the PWZ representation of
![]() $\tilde X^+_H$
in (7), we have
$\tilde X^+_H$
in (7), we have
 \begin{align} \mathbb{E}(\tilde X^+_H(\tau)) = \mathbb{E}\bigg( \tau^{H-({1}/{2})}B(\tau) - (H-({1}/{2})) \cdot \int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (B(\tau)-B(s))\,\textrm{d}s\bigg) \nonumber \\[5pt] = \mathbb{E}\bigg( \tau^{H-({1}/{2})}Y(\tau) + \frac{a\tau^{H+(1/2)}}{H+1/2} - \big(H-\tfrac{1}{2}\big) \cdot \int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (Y(\tau)-Y(s))\,\textrm{d}s\bigg), \end{align}
\begin{align} \mathbb{E}(\tilde X^+_H(\tau)) = \mathbb{E}\bigg( \tau^{H-({1}/{2})}B(\tau) - (H-({1}/{2})) \cdot \int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (B(\tau)-B(s))\,\textrm{d}s\bigg) \nonumber \\[5pt] = \mathbb{E}\bigg( \tau^{H-({1}/{2})}Y(\tau) + \frac{a\tau^{H+(1/2)}}{H+1/2} - \big(H-\tfrac{1}{2}\big) \cdot \int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (Y(\tau)-Y(s))\,\textrm{d}s\bigg), \end{align}
where in the second line we simply substituted
![]() $B(t) = Y(t)+at$
and integrated out
$B(t) = Y(t)+at$
and integrated out
![]() $\int_0^\tau (\tau-s)^{H-(3/2)}(a\tau-as)\,\textrm{d}s$
. Furthermore, notice that for any
$\int_0^\tau (\tau-s)^{H-(3/2)}(a\tau-as)\,\textrm{d}s$
. Furthermore, notice that for any
![]() $T\in(0,\infty)$
, the PWZ representation of
$T\in(0,\infty)$
, the PWZ representation of
![]() $\tilde X_H^-(\tau)$
from (7) can be rewritten as
$\tilde X_H^-(\tau)$
from (7) can be rewritten as
 \begin{align*} \tilde X_H^-(\tau) & \;:\!=\; -(T-\tau)^{H-(1/2)}(B(\tau)-B(T)) + \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-(3/2)}(B(\tau)-B(s))\,\textrm{d}s \\[5pt] & \quad + \big(H-\tfrac{1}{2}\big) \cdot \int_0^T s^{H-(3/2)}B(s)\,\textrm{d}s - T^{H-(1/2)}B(T) \\[5pt] & \quad + \big(H-\tfrac{1}{2}\big) \cdot \int_T^\infty [s^{H-(3/2)} - (s-\tau)^{H-(3/2)}] \cdot (B(s)-B(T))\,\textrm{d}s. \end{align*}
\begin{align*} \tilde X_H^-(\tau) & \;:\!=\; -(T-\tau)^{H-(1/2)}(B(\tau)-B(T)) + \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-(3/2)}(B(\tau)-B(s))\,\textrm{d}s \\[5pt] & \quad + \big(H-\tfrac{1}{2}\big) \cdot \int_0^T s^{H-(3/2)}B(s)\,\textrm{d}s - T^{H-(1/2)}B(T) \\[5pt] & \quad + \big(H-\tfrac{1}{2}\big) \cdot \int_T^\infty [s^{H-(3/2)} - (s-\tau)^{H-(3/2)}] \cdot (B(s)-B(T))\,\textrm{d}s. \end{align*}
Since Brownian motion is centred and has independent increments,
![]() $\tau$
is independent of
$\tau$
is independent of
![]() $\{B(T+s)-B(T)\;:\; s>0\}$
and the expected value of each term in the second and third lines above is equal to 0. This yields
$\{B(T+s)-B(T)\;:\; s>0\}$
and the expected value of each term in the second and third lines above is equal to 0. This yields
 \begin{align*} & \mathbb{E}(\tilde X_H^-(\tau)) \\[5pt] & = -\mathbb{E}\bigg((T-\tau)^{H-(1/2)}(B(\tau)-B(T)) - \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-(3/2)}(B(\tau)-B(s))\,\textrm{d}s\bigg). \end{align*}
\begin{align*} & \mathbb{E}(\tilde X_H^-(\tau)) \\[5pt] & = -\mathbb{E}\bigg((T-\tau)^{H-(1/2)}(B(\tau)-B(T)) - \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-(3/2)}(B(\tau)-B(s))\,\textrm{d}s\bigg). \end{align*}
After substituting
![]() $B(t)=Y(t)+at$
we find that this equals
$B(t)=Y(t)+at$
we find that this equals
 \begin{align*} & -\mathbb{E}\bigg((T-\tau)^{H-({1}/{2})}(Y(\tau)-Y(T)) \\[5pt] & - \frac{a(T-\tau)^{H+({1}/{2})}}{H+{1}/{2}} - \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-({3}/{2})}(Y(\tau)-Y(s))\,\textrm{d}s\bigg). \end{align*}
\begin{align*} & -\mathbb{E}\bigg((T-\tau)^{H-({1}/{2})}(Y(\tau)-Y(T)) \\[5pt] & - \frac{a(T-\tau)^{H+({1}/{2})}}{H+{1}/{2}} - \big(H-\tfrac{1}{2}\big) \cdot \int_\tau^T(s-\tau)^{H-({3}/{2})}(Y(\tau)-Y(s))\,\textrm{d}s\bigg). \end{align*}
Now let
![]() $\{\widehat Y(t)\;:\; t\in[0,T]\}$
be the time-reverse of process Y, i.e.
$\{\widehat Y(t)\;:\; t\in[0,T]\}$
be the time-reverse of process Y, i.e.
![]() $\widehat Y(t)\;:\!=\;Y(T-t)-Y(T)$
, and let
$\widehat Y(t)\;:\!=\;Y(T-t)-Y(T)$
, and let
![]() $\widehat\tau\;:\!=\;\textrm{arg max}\{t\in[0,T]\;:\;\widehat Y(t)\}$
be the time of its supremum over [0, T]. Notice that we must have
$\widehat\tau\;:\!=\;\textrm{arg max}\{t\in[0,T]\;:\;\widehat Y(t)\}$
be the time of its supremum over [0, T]. Notice that we must have
![]() $\tau^*= T-\tau$
. After substituting for
$\tau^*= T-\tau$
. After substituting for
![]() $\widehat Y$
, we find that
$\widehat Y$
, we find that
Finally, we notice that
![]() $\widehat Y(\!\cdot\!) \stackrel{\textrm{d}}{=} Y(\cdot\,;-a)$
, i.e.
$\widehat Y(\!\cdot\!) \stackrel{\textrm{d}}{=} Y(\cdot\,;-a)$
, i.e.
![]() $\widehat Y$
follows the law of drifted Brownian motion with drift
$\widehat Y$
follows the law of drifted Brownian motion with drift
![]() $-a$
. Comparing the above with (19) for
$-a$
. Comparing the above with (19) for
![]() $\mathbb{E}\tilde X^+_H(\tau)$
concludes the proof.
$\mathbb{E}\tilde X^+_H(\tau)$
concludes the proof.
In light of the result in Lemma 2 the function
![]() $\mathcal J^-_H(T,a)$
can be expressed using
$\mathcal J^-_H(T,a)$
can be expressed using
![]() $\mathcal J_H(T,a)$
, which justifies our notation
$\mathcal J_H(T,a)$
, which justifies our notation
![]() $\mathcal J_H(T,a)$
instead of
$\mathcal J_H(T,a)$
instead of
![]() $\mathcal J^+_H(T,a)$
, cf. (16). Before proving Proposition 3, we need to establish a certain continuity property of the argmax functional of Brownian motion. In what follows, let
$\mathcal J^+_H(T,a)$
, cf. (16). Before proving Proposition 3, we need to establish a certain continuity property of the argmax functional of Brownian motion. In what follows, let
![]() $\tau_{1/2}(T,a) \;:\!=\; \textrm{arg max}_{t\in[0,T]} \{B(t) - at\}$
be the argmax functional of drifted Brownian motion; see also the definition in (14).
$\tau_{1/2}(T,a) \;:\!=\; \textrm{arg max}_{t\in[0,T]} \{B(t) - at\}$
be the argmax functional of drifted Brownian motion; see also the definition in (14).
Lemma 3.
-
(i)
 $\lim_{a\to a^*}\tau_{1/2}(T,a) = \tau_{1/2}(T,a^*)$
a.s. for any
$\lim_{a\to a^*}\tau_{1/2}(T,a) = \tau_{1/2}(T,a^*)$
a.s. for any
 $T\in(0,\infty)$
,
$T\in(0,\infty)$
,
 $a^{\ast}\in\mathbb{R}$
.
$a^{\ast}\in\mathbb{R}$
. -
(ii)
 $\lim_{T\to \infty} \tau_{1/2}(T,a) = \tau_{1/2}(\infty,a)$
a.s. for any
$\lim_{T\to \infty} \tau_{1/2}(T,a) = \tau_{1/2}(\infty,a)$
a.s. for any
 $a>0$
.
$a>0$
.
Proof. Let
![]() $Y(t;\;a) \;:\!=\; B(t)-at$
. It is easy to see that the trajectories
$Y(t;\;a) \;:\!=\; B(t)-at$
. It is easy to see that the trajectories
![]() $\{Y(t,a)\;:\; t\in[0,T]\}$
converge uniformly to
$\{Y(t,a)\;:\; t\in[0,T]\}$
converge uniformly to
![]() $\{Y(t,a^*)\;:\; t\in[0,T]\}$
as
$\{Y(t,a^*)\;:\; t\in[0,T]\}$
as
![]() $a\to a^*$
, and hence the argmax functionals also converge; see, e.g., [Reference Seijo and Sen22, Lemma 2.9], which concludes the proof of item (i). Furthermore, since
$a\to a^*$
, and hence the argmax functionals also converge; see, e.g., [Reference Seijo and Sen22, Lemma 2.9], which concludes the proof of item (i). Furthermore, since
![]() $\tau_{1/2}(\infty,a)$
is almost surely finite, then there must exist some (random)
$\tau_{1/2}(\infty,a)$
is almost surely finite, then there must exist some (random)
![]() $T_0>0$
such that
$T_0>0$
such that
![]() $\tau_{1/2}(T,a) = \tau_{1/2}(\infty,a)$
for all
$\tau_{1/2}(T,a) = \tau_{1/2}(\infty,a)$
for all
![]() $T>T_0$
, which implies item (ii).
$T>T_0$
, which implies item (ii).
Proof of Proposition
3. Consider the case
![]() $H=\tfrac{1}{2}$
. Since the value of
$H=\tfrac{1}{2}$
. Since the value of
![]() $\mathscr M_{1/2}(T,a)$
is irrespective of
$\mathscr M_{1/2}(T,a)$
is irrespective of
![]() $\boldsymbol{c}$
(see also the comment above (15)), we may take
$\boldsymbol{c}$
(see also the comment above (15)), we may take
![]() $\boldsymbol{c} = (1,0)$
and observe that
$\boldsymbol{c} = (1,0)$
and observe that
 \begin{align*} \mathscr M_{1/2}(T,a) & = \mathbb{E} \big(M^{(1,0)}_{1/2}(T,a)\big) = \mathbb{E} \big(B^{(1,0)}_{1/2}(\tau_{1/2}(T,a)) - a\tau_{1/2}(T,a)\big) \\[5pt] & = \frac{\mathbb{E}(\tilde X^+_{1/2}(\tau(T,a)))}{\sqrt{V^{(1,0)}_{1/2}}} - a\mathbb{E}\left(\tau_{1/2}(T,a)\right) \\[5pt] & = \mathcal J_{1/2}(T,a) - a\mathcal E_{1/2}(T,a); \end{align*}
\begin{align*} \mathscr M_{1/2}(T,a) & = \mathbb{E} \big(M^{(1,0)}_{1/2}(T,a)\big) = \mathbb{E} \big(B^{(1,0)}_{1/2}(\tau_{1/2}(T,a)) - a\tau_{1/2}(T,a)\big) \\[5pt] & = \frac{\mathbb{E}(\tilde X^+_{1/2}(\tau(T,a)))}{\sqrt{V^{(1,0)}_{1/2}}} - a\mathbb{E}\left(\tau_{1/2}(T,a)\right) \\[5pt] & = \mathcal J_{1/2}(T,a) - a\mathcal E_{1/2}(T,a); \end{align*}
therefore
![]() $\mathcal J_{1/2}(T,a) = \mathscr M_{1/2}(T,a) + a\mathcal E_{1/2}(T,a)$
, which agrees with Proposition 2 (note that the error function is a special case of the incomplete Gamma function, cf. (34)).
$\mathcal J_{1/2}(T,a) = \mathscr M_{1/2}(T,a) + a\mathcal E_{1/2}(T,a)$
, which agrees with Proposition 2 (note that the error function is a special case of the incomplete Gamma function, cf. (34)).
Now let
![]() $H\in\big(0,\tfrac{1}{2}\big)\cup\big(\tfrac{1}{2},1\big)$
. For brevity, we write
$H\in\big(0,\tfrac{1}{2}\big)\cup\big(\tfrac{1}{2},1\big)$
. For brevity, we write
![]() $\tau \;:\!=\; \tau_{1/2}(T,a)$
and let
$\tau \;:\!=\; \tau_{1/2}(T,a)$
and let
![]() $Y(t) = B(t)-at$
. We now consider the case
$Y(t) = B(t)-at$
. We now consider the case
![]() $T\in(0,\infty)$
,
$T\in(0,\infty)$
,
![]() $a\neq0$
. Recall that, from (19), we have
$a\neq0$
. Recall that, from (19), we have
Now, we have
 \begin{align*} & \mathbb{E}\bigg(\int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (Y(\tau)-Y(s))\,\textrm{d}s\bigg) \\[5pt] & = \mathbb{E}\bigg(\mathbb{E}\bigg(\int_0^t (t-s)^{H-({3}/{2})} \cdot (Y(t)-Y(s))\,\textrm{d}s \mid \tau=t,\,Y(\tau)=y\bigg)\bigg). \end{align*}
\begin{align*} & \mathbb{E}\bigg(\int_0^\tau (\tau-s)^{H-({3}/{2})} \cdot (Y(\tau)-Y(s))\,\textrm{d}s\bigg) \\[5pt] & = \mathbb{E}\bigg(\mathbb{E}\bigg(\int_0^t (t-s)^{H-({3}/{2})} \cdot (Y(t)-Y(s))\,\textrm{d}s \mid \tau=t,\,Y(\tau)=y\bigg)\bigg). \end{align*}
We now recognise that the above equals
![]() $\mathbb{E}(I_H(\tau,Y(\tau))$
, with
$\mathbb{E}(I_H(\tau,Y(\tau))$
, with
![]() $I_H(t,y)$
defined in (13). Using Lemma 1 we obtain
$I_H(t,y)$
defined in (13). Using Lemma 1 we obtain
![]() $\mathcal J_H(T,a) = \mathcal J_H^{(1)}(T,a) + \mathcal J_H^{(2)}(T,a)$
, where
$\mathcal J_H(T,a) = \mathcal J_H^{(1)}(T,a) + \mathcal J_H^{(2)}(T,a)$
, where
 \begin{align*} \mathcal J_H^{(1)}(T,a) & \;:\!=\; \frac{1}{H+{1}/{2}} \cdot \mathbb{E} \bigg(\tau^{H-({1}/{2})}\bigg(Y(\tau) + a\tau - \frac{\tau}{Y(\tau)}\bigg)\bigg), \\[5pt] \mathcal J_H^{(2)}(T,a) & \;:\!=\; \frac{1}{H+{1}/{2}} \cdot \mathbb{E}\bigg(\frac{\tau^{H+({1}/{2})}}{Y(\tau)} \cdot \frac{\Gamma(H)}{\sqrt{\pi}} U\bigg(H-\frac{1}{2},\frac{1}{2},\frac{Y^2(\tau)}{2\tau}\bigg)\bigg). \end{align*}
\begin{align*} \mathcal J_H^{(1)}(T,a) & \;:\!=\; \frac{1}{H+{1}/{2}} \cdot \mathbb{E} \bigg(\tau^{H-({1}/{2})}\bigg(Y(\tau) + a\tau - \frac{\tau}{Y(\tau)}\bigg)\bigg), \\[5pt] \mathcal J_H^{(2)}(T,a) & \;:\!=\; \frac{1}{H+{1}/{2}} \cdot \mathbb{E}\bigg(\frac{\tau^{H+({1}/{2})}}{Y(\tau)} \cdot \frac{\Gamma(H)}{\sqrt{\pi}} U\bigg(H-\frac{1}{2},\frac{1}{2},\frac{Y^2(\tau)}{2\tau}\bigg)\bigg). \end{align*}
The joint density of the pair
![]() $(\tau,Y(\tau))$
is well known (see (11) in Section 2.2) and therefore both functions
$(\tau,Y(\tau))$
is well known (see (11) in Section 2.2) and therefore both functions
![]() $\mathcal J_H^{(1)}(T,a)$
and
$\mathcal J_H^{(1)}(T,a)$
and
![]() $\mathcal J_H^{(2)}(T,a)$
can be written as definite integrals and calculated. In fact, we have
$\mathcal J_H^{(2)}(T,a)$
can be written as definite integrals and calculated. In fact, we have
The derivation of (20) is purely calculational and is provided in Appendix B (available in the Supplementary Material of the online version of this manuscript). This ends the proof in the case
![]() $T\in(0,\infty)$
,
$T\in(0,\infty)$
,
![]() $a\neq 0$
.
$a\neq 0$
.
In order to derive the formula for
![]() $\mathcal J_H(T,a)$
in the remaining two cases (i.e.
$\mathcal J_H(T,a)$
in the remaining two cases (i.e.
![]() $T\in(0,\infty)$
,
$T\in(0,\infty)$
,
![]() $a=0$
and
$a=0$
and
![]() $T=\infty$
,
$T=\infty$
,
![]() $a>0$
), we could redo the calculations in (20) with appropriate density functions for the pair
$a>0$
), we could redo the calculations in (20) with appropriate density functions for the pair
![]() $(\tau,Y(\tau))$
; see (12) and (11). However, this is not necessary, as it suffices to show that the function
$(\tau,Y(\tau))$
; see (12) and (11). However, this is not necessary, as it suffices to show that the function
![]() $\mathcal J_H(T,a)$
is continuous at
$\mathcal J_H(T,a)$
is continuous at
![]() $(\infty,a)$
and (T, 0).
$(\infty,a)$
and (T, 0).
Let
![]() $T\in(0,\infty)$
,
$T\in(0,\infty)$
,
![]() $a=0$
. Using the fact that
$a=0$
. Using the fact that
![]() $\gamma(s,x) \sim (sx^s)^{-1}$
as
$\gamma(s,x) \sim (sx^s)^{-1}$
as
![]() $x\downarrow0$
, we can see that
$x\downarrow0$
, we can see that
Showing that
![]() $\lim_{a\to0}\mathcal J_H(T,a) = \mathcal J_H(T,0)$
would therefore conclude the proof in this case. By definition we have
$\lim_{a\to0}\mathcal J_H(T,a) = \mathcal J_H(T,0)$
would therefore conclude the proof in this case. By definition we have
![]() $\mathcal J_H(T,a) = \sqrt{V(H)} \cdot \mathbb{E} \big(B^{(1,0)}_H(\tau(T,a))\big)$
. Since V(H) is continuous at
$\mathcal J_H(T,a) = \sqrt{V(H)} \cdot \mathbb{E} \big(B^{(1,0)}_H(\tau(T,a))\big)$
. Since V(H) is continuous at
![]() $H=\tfrac{1}{2}$
, it suffices to show that
$H=\tfrac{1}{2}$
, it suffices to show that
as
![]() $a\to 0$
. Using Proposition 1 and Lemma 3(i), we obtain
$a\to 0$
. Using Proposition 1 and Lemma 3(i), we obtain
Moreover, for any
![]() $\varepsilon>0$
and all
$\varepsilon>0$
and all
![]() $a\in(\!-\!\varepsilon,\varepsilon)$
we have
$a\in(\!-\!\varepsilon,\varepsilon)$
we have
which has finite expectation. Therefore, by Lebesgue dominated convergence we can conclude that the limit in (21) holds, which ends the proof in this case.
Let
![]() $T=\infty$
,
$T=\infty$
,
![]() $a>0$
. It is easy to see that
$a>0$
. It is easy to see that
Analogously to the proof of the previous case, it suffices to show that
as
![]() $T\to\infty$
. Using Proposition 1 and Lemma 3(ii), we find that
$T\to\infty$
. Using Proposition 1 and Lemma 3(ii), we find that
Moreover, since the mapping
![]() $T\mapsto\tau(T,a)$
is non-decreasing, we have
$T\mapsto\tau(T,a)$
is non-decreasing, we have
and the right-hand side above has a finite expectation. Using Lebesgue dominated convergence we conclude that the limit (22) holds, which ends the proof.
Proof of Proposition
4. From the definition of
![]() $m^\boldsymbol{c}_H(T,a)$
in (15),
$m^\boldsymbol{c}_H(T,a)$
in (15),
In the light of Lemma 2, for
![]() $T\in(0,\infty)$
we have (17). We now show that (17) also holds in the case
$T\in(0,\infty)$
we have (17). We now show that (17) also holds in the case
![]() $T=\infty$
,
$T=\infty$
,
![]() $a>0$
. Using Proposition 1 and Lemma 3(ii), we find that
$a>0$
. Using Proposition 1 and Lemma 3(ii), we find that
Now we have the bound
![]() $\tilde B^\boldsymbol{c}_H(\tau(T,a)) - a\tau(T,a) \leq M^\boldsymbol{c}_{H}(\infty,a)$
, which is integrable, and hence we can conclude that
$\tilde B^\boldsymbol{c}_H(\tau(T,a)) - a\tau(T,a) \leq M^\boldsymbol{c}_{H}(\infty,a)$
, which is integrable, and hence we can conclude that
![]() $m^\boldsymbol{c}_H(\infty,a) = \lim_{T\to\infty} m^\boldsymbol{c}_H(T,a)$
. Furthermore, from Propositions 3 and 2 it is clear that
$m^\boldsymbol{c}_H(\infty,a) = \lim_{T\to\infty} m^\boldsymbol{c}_H(T,a)$
. Furthermore, from Propositions 3 and 2 it is clear that
![]() $\mathcal J_H(T,a) \to \mathcal J_H(\infty,a)$
and
$\mathcal J_H(T,a) \to \mathcal J_H(\infty,a)$
and
![]() $\mathcal E_{1/2}(T,a) \to \mathcal E_{1/2}(\infty,a)$
as
$\mathcal E_{1/2}(T,a) \to \mathcal E_{1/2}(\infty,a)$
as
![]() $T\to\infty$
. Hence,
$T\to\infty$
. Hence,
which concludes the proof that (17) holds for all admissible pairs (T, a).
Finally, since
![]() $J_H(T,a)>0$
(see Proposition 3), it is easy to see that (17) is maximized whenever
$J_H(T,a)>0$
(see Proposition 3), it is easy to see that (17) is maximized whenever
![]() $({c_+}-{c_-})/\sqrt{V^\boldsymbol{c}_H}$
is maximized. It is straighforward to show that the maximum is attained at
$({c_+}-{c_-})/\sqrt{V^\boldsymbol{c}_H}$
is maximized. It is straighforward to show that the maximum is attained at
![]() $\boldsymbol{c}=(1,-1)$
, which concludes the proof.
$\boldsymbol{c}=(1,-1)$
, which concludes the proof.
Appendix A. Special functions
All of the definitions, formulae, and relations from this section can be found in [Reference Abramowitz and Stegun1].
A.1. Confluent hypergeometric functions
For any
![]() $a,z\in\mathbb{R}$
and
$a,z\in\mathbb{R}$
and
![]() $b\in\mathbb{R}\setminus\{0,-1,-2,\ldots\}$
we define Kummer’s (confluent hypergeometric) function
$b\in\mathbb{R}\setminus\{0,-1,-2,\ldots\}$
we define Kummer’s (confluent hypergeometric) function
where
![]() $a^{(n)}$
is the rising factorial, i.e.
$a^{(n)}$
is the rising factorial, i.e.
![]() $a^{(0)} \;:\!=\; 1$
and
$a^{(0)} \;:\!=\; 1$
and
![]() $a^{(n)}\;:\!=\;a(a+1)\cdots(a+n-1)$
for
$a^{(n)}\;:\!=\;a(a+1)\cdots(a+n-1)$
for
![]() $n\in\mathbb{N}$
. Similarly, for any
$n\in\mathbb{N}$
. Similarly, for any
![]() $a,z\in\mathbb{R}$
and
$a,z\in\mathbb{R}$
and
![]() $b\in\mathbb{R}\setminus\{0,-1,-2,\ldots\}$
we define Tricomi’s (confluent hypergeometric) function
$b\in\mathbb{R}\setminus\{0,-1,-2,\ldots\}$
we define Tricomi’s (confluent hypergeometric) function
When
![]() $b>a>0$
, Kummer’s function can be represented as an integral,
$b>a>0$
, Kummer’s function can be represented as an integral,
similarly, for
![]() $a>0$
,
$a>0$
,
![]() $z>0$
, Tricomi’s function can be represented as an integral,
$z>0$
, Tricomi’s function can be represented as an integral,
Moreover, we have the Kummer transformations
and the recurrence relations
In this manuscript we often use the following integral equality. Let
![]() $c>\gamma>0$
and
$c>\gamma>0$
and
![]() $u>0$
; then
$u>0$
; then
which can be verified using [Reference Gradshteyn and Ryzhik13, 7.613-1].
A.2. Incomplete Gamma function
For any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $z>0$
, we define the upper and lower incomplete Gamma functions respectively as
$z>0$
, we define the upper and lower incomplete Gamma functions respectively as
so that
![]() $\Gamma(\alpha,z)+\gamma(\alpha,z)=\Gamma(\alpha)$
, where
$\Gamma(\alpha,z)+\gamma(\alpha,z)=\Gamma(\alpha)$
, where
![]() $\Gamma(\!\cdot\!)$
the standard Gamma function
$\Gamma(\!\cdot\!)$
the standard Gamma function
![]() $\Gamma(\alpha)\;:\!=\;\int_0^\infty t^{\alpha-1}\textrm{e}^{-t}\,\textrm{d}t$
. Using integration by parts we obtain the useful recurrence relation
$\Gamma(\alpha)\;:\!=\;\int_0^\infty t^{\alpha-1}\textrm{e}^{-t}\,\textrm{d}t$
. Using integration by parts we obtain the useful recurrence relation
Notice that, as
![]() $z\to\infty$
, this is reduced to the well-known recurrence relation for the Gamma function, i.e.
$z\to\infty$
, this is reduced to the well-known recurrence relation for the Gamma function, i.e.
![]() $\Gamma(\alpha+1) = \alpha\Gamma(\alpha)$
. Finally, we note that
$\Gamma(\alpha+1) = \alpha\Gamma(\alpha)$
. Finally, we note that
![]() $\gamma(\alpha,z)$
can be expressed in terms of the confluent hypergeometric function:
$\gamma(\alpha,z)$
can be expressed in terms of the confluent hypergeometric function:
A.3. Error function
For
![]() $z\in\mathbb{R}$
we define the error function and complementary error function, respectively, as
$z\in\mathbb{R}$
we define the error function and complementary error function, respectively, as
The error function can be expressed in terms of the incomplete Gamma function, and therefore, in the light of (33), also in terms of the hypergeometric function:
Acknowledgements
The author would like to thank Prof. Krzysztof Dȩbicki and Prof. Tomasz Rolski for helpful discussions, and the anonymous referees for their careful reading of the manuscript.
Funding information
Krzysztof Bisewski’s research was funded by SNSF Grant 200021-196888.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Supplementary material
The Supplementary Material for this article, which contains Appendix B, can be found at https://doi.org/10.1017/jpr.2022.129.