No CrossRef data available.
Published online by Cambridge University Press: 23 September 2021
We compare the solutions of two Poisson problems in a spherical shell with Robin boundary conditions, one with given data, and one where the data have been cap symmetrized. When the Robin parameters are nonnegative, we show that the solution to the symmetrized problem has larger convex means. Sending one of the Robin parameters to
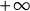 $+\infty $
, we obtain mixed Robin/Dirichlet comparison results in shells. We prove similar results on balls and prove a comparison principle on generalized cylinders with mixed Robin/Neumann boundary conditions.
$+\infty $
, we obtain mixed Robin/Dirichlet comparison results in shells. We prove similar results on balls and prove a comparison principle on generalized cylinders with mixed Robin/Neumann boundary conditions.