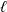1. Introduction
Recursive trees are rooted labelled trees that are increasing; that is, starting at a distinguished root vertex labelled 0, nodes are labelled in increasing order away from the root. Recursive trees generated using stochastic processes have attracted widespread study, motivated by, for example, their applications to the evolution of languages [Reference Najock and Heyde29], the analysis of algorithms [Reference Mahmoud25], and the study of complex networks (see, for example, [Reference Van der Hofstad38, Chapter 8.1]). Other applications include modelling the spread of epidemics, modelling pyramid schemes, and constructing family trees of ancient manuscripts (e.g. [Reference Drmota15, p. 14]).
A common framework for randomly generating recursive trees is to have vertices arrive one at a time and each connect to an existing vertex in the tree, selected according to some probability distribution. In the uniform recursive tree, introduced by Na and Rapoport in [Reference Na and Rapoport28], existing vertices are chosen uniformly at random, whilst the well-known random ordered recursive tree, introduced by Prodinger and Urbanek in [Reference Prodinger and Urbanek32], may be interpreted as having existing vertices chosen with probability proportional to their degree. The latter model has been studied and rediscovered in various guises: under the names nonuniform recursive trees by Szymański in [Reference Szymański36], random plane-oriented recursive trees in [Reference Mahmoud24, Reference Mahmoud, Smythe and Szymański26], random heap-ordered recursive trees in [Reference Chen and Ni10], and scale-free trees in [Reference Bollobás and Riordan6, Reference Bollobás, Riordan, Spencer and Tusnády7, Reference Szabó, Alava and Kertész35]. Random ordered recursive trees, or plane-oriented recursive trees, are so named because the process stopped after n vertices arrive is distributed like a tree chosen at random from the set of rooted labelled trees on n vertices embedded in the plane where descendants of a node are ordered from left to right. However, as first observed by Albert and Barabási in [Reference Barabási and Albert2] and studied in a mathematically precise way in [Reference Bollobás, Riordan, Spencer and Tusnády7, Reference Móri27], these trees, and more generally graphs evolving according to a similar mechanism, possess many interesting, non-trivial properties of real-world networks. These properties include having a power law degree distribution with exponent between 2 and 3 and a diameter that scales logarithmically in the number of vertices. The latter may be interpreted as a ‘small-world’ phenomenon: although the size of the network is large, the diameter of the network remains relatively small. In this context, the fact that vertices are chosen according to their degree may be interpreted as the network showing ‘preference’ for vertices of high degree; hence the model is often called preferential attachment. This model has been generalised in a number of ways, to encompass the cases where vertices are chosen according to a super-linear function of their degree [Reference Oliveira and Spencer31] and a sub-linear function of their degree [Reference Dereich and Mörters13], or indeed any positive function of the degree [Reference Rudas, Tóth and Valkó33]. In [Reference Holmgren and Janson20], this model is generalised to possibly non-negative functions of the degree and is referred to as generalised preferential attachment.
In applications, it is often interesting to add weights to vertices as a measure of the intrinsic ‘fitness’ of the node the vertex represents. In the Bianconi–Barabási model, or preferential attachment with multiplicative fitness, introduced in [Reference Bianconi and Barabási5] and studied in a mathematically precise way in [Reference Bhamidi3, Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich11, Reference Dereich, Mailler and Mörters12, Reference Dereich and Ortgiese14], vertices are equipped with independent, identically distributed (i.i.d.) weights and connect to previous vertices with probability proportional to the product of their weight and their degree. Interestingly, as observed in [Reference Bianconi and Barabási5] and confirmed rigorously in [Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich, Mailler and Mörters12, Reference Dereich and Ortgiese14], there is a critical condition on the weight distribution under which this model undergoes a phase transition, resulting in a Bose–Einstein condensation: in the limit, a positive fraction of vertices accumulate around vertices of maximum weight. In a similar model known as preferential attachment with additive fitness, introduced in [Reference Ergün and Rodgers16] and studied mathematically in [Reference Bhamidi3, Reference Lodewijks and Ortgiese23, Reference Sénizergues34], vertices connect to previous vertices with probability proportional to the sum of their degree (or degree minus one) and their weight. A number of other interesting preferential attachment models with fitness have been studied, including a related continuous-time model which incorporates ageing of vertices [Reference Garavaglia, van der Hofstad and Woeginger18] and discrete-time models with co-existing additive and multiplicative attachment rules [Reference Antunović, Mossel and Rácz1, Reference Jordan22].
Adding weights also allows for a generalisation of the uniform recursive tree called the weighted recursive tree, where now vertices connect to previous vertices with probability proportional to their weight. This model was introduced in [Reference Borovkov and Vatutin9] for specific types of weights and in [Reference Hiesmayr and Işlak19] in full generality. It was also introduced independently by Janson in the case that all weights are one except at the root, motivated by applications to infinite-colour Pólya urns [Reference Janson21]. In [Reference Sénizergues34], Sénizergues showed that a preferential attachment tree with additive fitness with deterministic weights is equal in distribution to an associated weighted random recursive tree with random weights, an interesting link between the two classes of models.
Motivated by applications to invasive percolation models in physics, Bianconi [Reference Bianconi4] introduced a similar model of growing Cayley trees. In this model, vertices are equipped with independent weights and are either active or inactive. At each time-step an active vertex is chosen with probability proportional to its weight, produces
![]() $\ell$
new vertices with weights of their own, and then becomes inactive. Bianconi observed that in this model, the distribution of weights of active vertices converges to a Fermi–Dirac distribution, in contrast to the Bose distribution that emerges in the Bianconi–Barabási model.
$\ell$
new vertices with weights of their own, and then becomes inactive. Bianconi observed that in this model, the distribution of weights of active vertices converges to a Fermi–Dirac distribution, in contrast to the Bose distribution that emerges in the Bianconi–Barabási model.
1.1. Notation
Generally in this paper we set
![]() $\mathbb{N}_{0} \,:\!=\, \mathbb{N} \cup \{0\}$
and
$\mathbb{N}_{0} \,:\!=\, \mathbb{N} \cup \{0\}$
and
![]() $\mathbb{R}_{+} \,:\!=\, [0, \infty)$
. We assume that
$\mathbb{R}_{+} \,:\!=\, [0, \infty)$
. We assume that
![]() $\mathbb{R}_{+}$
is equipped with the usual Borel sigma-algebra, and
$\mathbb{R}_{+}$
is equipped with the usual Borel sigma-algebra, and
![]() $\mu$
will denote a fixed probability measure on
$\mu$
will denote a fixed probability measure on
![]() $\mathbb{R}_{+}$
. Also, in general in this paper, W refers to a generic
$\mathbb{R}_{+}$
. Also, in general in this paper, W refers to a generic
![]() $\mu$
-distributed random variable. Finally, we generally refer to an element of the Borel sigma-field as a measurable set. Given such a set A, we denote by
$\mu$
-distributed random variable. Finally, we generally refer to an element of the Borel sigma-field as a measurable set. Given such a set A, we denote by
![]() $\mathbf{1}_{A}(x)$
the indicator function associated with the set, so that
$\mathbf{1}_{A}(x)$
the indicator function associated with the set, so that
![]() $\mathbf{1}_{A}(x) = 1$
if
$\mathbf{1}_{A}(x) = 1$
if
![]() $x \in A$
and 0 otherwise. Moreover, if
$x \in A$
and 0 otherwise. Moreover, if
![]() $\mathbf{1}_{A}(x)$
is a random variable on a probability space
$\mathbf{1}_{A}(x)$
is a random variable on a probability space
![]() $(\Omega, \mathbb{F}, \mathbb{P})$
, we often omit the dependence on
$(\Omega, \mathbb{F}, \mathbb{P})$
, we often omit the dependence on
![]() $x \in \Omega$
, and simply write
$x \in \Omega$
, and simply write
![]() $\mathbf{1}_{A}$
.
$\mathbf{1}_{A}$
.
1.2. Description of model
The goal of this paper is to present a unified model that encompasses most of the models described in the introduction above. In order to define the model, we first require a probability measure
![]() $\mu$
supported on
$\mu$
supported on
![]() $\mathbb{R}_{+}$
and a fitness function, which is a function
$\mathbb{R}_{+}$
and a fitness function, which is a function
![]() $f\,:\, \mathbb{N}_0 \times \mathbb{R}_{+} \rightarrow \mathbb{R}_+$
. We consider evolving sequences of weighted oriented trees
$f\,:\, \mathbb{N}_0 \times \mathbb{R}_{+} \rightarrow \mathbb{R}_+$
. We consider evolving sequences of weighted oriented trees
![]() ${\mathcal{T}} \,:\!=\, \left(\mathcal{T}_{t}\right)_{t \in \mathbb{N}_0}$
; these are trees with directed edges, where vertices have real-valued weights assigned to them. The model also has an additional parameter
${\mathcal{T}} \,:\!=\, \left(\mathcal{T}_{t}\right)_{t \in \mathbb{N}_0}$
; these are trees with directed edges, where vertices have real-valued weights assigned to them. The model also has an additional parameter
![]() $\ell \in \mathbb{N}$
. We start with an initial tree
$\ell \in \mathbb{N}$
. We start with an initial tree
![]() $\mathcal{T}_0$
consisting of a single vertex 0 with weight
$\mathcal{T}_0$
consisting of a single vertex 0 with weight
![]() $W_0$
sampled from
$W_0$
sampled from
![]() $\mu$
. To ensure that the evolution of the model is well-defined, for brevity, we assume
$\mu$
. To ensure that the evolution of the model is well-defined, for brevity, we assume
![]() $f(0,W_0) > 0$
almost surely. Then we define
$f(0,W_0) > 0$
almost surely. Then we define
![]() $\mathcal{T}_{t+1}$
recursively as follows:
$\mathcal{T}_{t+1}$
recursively as follows:
-
(i) Sample a vertex j from
 $\mathcal{T}_t$
with probability where
$\mathcal{T}_t$
with probability where \begin{equation*}\frac{f({\text{deg}^{+}({j,\mathcal{T}_t})}/\ell, W_j)}{{\mathcal{Z}}_{t}},\end{equation*}
\begin{equation*}\frac{f({\text{deg}^{+}({j,\mathcal{T}_t})}/\ell, W_j)}{{\mathcal{Z}}_{t}},\end{equation*}
 ${\text{deg}^{+}({j,\mathcal{T}_t})}$
denotes the out-degree of the vertex j in the oriented tree
${\text{deg}^{+}({j,\mathcal{T}_t})}$
denotes the out-degree of the vertex j in the oriented tree
 ${\mathcal{T}}_t$
, and
${\mathcal{T}}_t$
, and
 $\mathcal{Z}_t \,:\!=\, \sum_{j=0}^{\ell t} f({\text{deg}^{+}({j,\mathcal{T}_t)/\ell, W_j})}$
is the partition function associated with the process.
$\mathcal{Z}_t \,:\!=\, \sum_{j=0}^{\ell t} f({\text{deg}^{+}({j,\mathcal{T}_t)/\ell, W_j})}$
is the partition function associated with the process.
-
(ii) Introduce
 $\ell$
new vertices
$\ell$
new vertices
 $t+1, t+2, \ldots, t+\ell$
with weights
$t+1, t+2, \ldots, t+\ell$
with weights
 $W_{t+1}, W_{t+2}, \ldots, W_{t+\ell}$
sampled independently from
$W_{t+1}, W_{t+2}, \ldots, W_{t+\ell}$
sampled independently from
 $\mu$
and the directed edges
$\mu$
and the directed edges
 $(j, t+1), (j, t+2), \ldots, (j,t + \ell)$
oriented towards the newly arriving vertices. We say that j is the parent of the new-coming vertices.
$(j, t+1), (j, t+2), \ldots, (j,t + \ell)$
oriented towards the newly arriving vertices. We say that j is the parent of the new-coming vertices.
Note that, since
![]() $\ell$
new vertices are connected to a parent at each time-step, for any vertex i in the tree,
$\ell$
new vertices are connected to a parent at each time-step, for any vertex i in the tree,
![]() $\ell$
divides the out-degree of i. Moreover, the evolution of the out-degree of vertex i with weight
$\ell$
divides the out-degree of i. Moreover, the evolution of the out-degree of vertex i with weight
![]() $W_i$
is determined by the values
$W_i$
is determined by the values
![]() $(f(j, W_i))_{j \in \mathbb{N}_0}$
. In general, when the distribution
$(f(j, W_i))_{j \in \mathbb{N}_0}$
. In general, when the distribution
![]() $\mu$
, fitness function f, and
$\mu$
, fitness function f, and
![]() $\ell$
are specified, we refer to this model as a
$\ell$
are specified, we refer to this model as a
![]() $(\mu,f, \ell)$
-recursive tree with independent fitnesses, often abbreviated as a ‘
$(\mu,f, \ell)$
-recursive tree with independent fitnesses, often abbreviated as a ‘
![]() ${\left({\mu, f,\ell}\right)}$
-RIF tree’ for brevity. Here ‘independent fitnesses’ refers to the fact that the fitness associated with a given vertex does not depend on the weights of its neighbours, in contrast to, for example, the models of dynamical simplicial complexes studied in [Reference Fountoulakis, Iyer, Mailler and Sulzbach17].
${\left({\mu, f,\ell}\right)}$
-RIF tree’ for brevity. Here ‘independent fitnesses’ refers to the fact that the fitness associated with a given vertex does not depend on the weights of its neighbours, in contrast to, for example, the models of dynamical simplicial complexes studied in [Reference Fountoulakis, Iyer, Mailler and Sulzbach17].
Remark 1.1. If we adopt the convention that the process terminates when no vertex can be chosen in the next step, the assumption that
![]() $f(0,W_0) > 0$
almost surely may be dropped in many places in this paper, if we condition on the event that the number of vertices in the tree tends to infinity as
$f(0,W_0) > 0$
almost surely may be dropped in many places in this paper, if we condition on the event that the number of vertices in the tree tends to infinity as
![]() $t \to \infty$
.
$t \to \infty$
.
Remark 1.2. In this model, the law of the sequence
![]() $(f(k,W))_{k\in \mathbb{N}_0}$
is more important than the function f. It is possible, for example, to define this model so that
$(f(k,W))_{k\in \mathbb{N}_0}$
is more important than the function f. It is possible, for example, to define this model so that
![]() $(f(k,W))_{k\in \mathbb{N}_0}$
is any law on
$(f(k,W))_{k\in \mathbb{N}_0}$
is any law on
![]() $\mathbb{R}_{+}^{\mathbb{N}_0}$
depending on W, even if one cannot write f explicitly, and as long as the sequences associated with different vertices are independent. For example, the sequence could be any stochastic process indexed by the non-negative integers, depending on an initial source of randomness W.
$\mathbb{R}_{+}^{\mathbb{N}_0}$
depending on W, even if one cannot write f explicitly, and as long as the sequences associated with different vertices are independent. For example, the sequence could be any stochastic process indexed by the non-negative integers, depending on an initial source of randomness W.
1.3. Quantities of interest studied in this paper
In this section, we will introduce the main quantities we will be interested in studying in this paper, along with some important definitions. Note that the definitions we introduce in this section will depend on the underlying parameters of the tree,
![]() $\mu$
, f, and
$\mu$
, f, and
![]() $\ell$
.
$\ell$
.
In this paper we will generally be concerned with the limiting behaviour of the following quantities:
-
1. Given a Borel set
 $B \subseteq \mathbb{R}_{+}$
, the quantity
$B \subseteq \mathbb{R}_{+}$
, the quantity
 $N_{k}(t,B)$
denotes the number of vertices v in the tree
$N_{k}(t,B)$
denotes the number of vertices v in the tree
 ${\mathcal{T}}_t$
with out-degree
${\mathcal{T}}_t$
with out-degree
 $k \ell$
and weight
$k \ell$
and weight
 $W_v \in B$
; that is, (1)
$W_v \in B$
; that is, (1) \begin{equation} N_{k}(t, B) \,:\!=\, \sum_{v \in \mathcal{T}_{t}\,:\, \deg^{+}(v, {\mathcal{T}}_{t}) = k\ell} \mathbf{1}_{B}(W_v).\end{equation}
\begin{equation} N_{k}(t, B) \,:\!=\, \sum_{v \in \mathcal{T}_{t}\,:\, \deg^{+}(v, {\mathcal{T}}_{t}) = k\ell} \mathbf{1}_{B}(W_v).\end{equation}
-
2. Given a Borel set
 $B \subseteq \mathbb{R}_{+}$
, the quantity
$B \subseteq \mathbb{R}_{+}$
, the quantity
 $\Xi(t,B)$
denotes the number of directed edges (v, v
′) in the tree
$\Xi(t,B)$
denotes the number of directed edges (v, v
′) in the tree
 ${\mathcal{T}}_t$
such that
${\mathcal{T}}_t$
such that
 $W_v \in B$
; that is, (2)
$W_v \in B$
; that is, (2) \begin{equation}\Xi(t,B) \,:\!=\, \sum_{(v,v^{\prime}) \in \mathcal{T}_{t}} \mathbf{1}_{B}(W_v).\end{equation}
\begin{equation}\Xi(t,B) \,:\!=\, \sum_{(v,v^{\prime}) \in \mathcal{T}_{t}} \mathbf{1}_{B}(W_v).\end{equation}
Now, reasoning informally and non-rigorously for a moment, suppose that W takes finitely many values. In addition, suppose that for all
![]() $t \geq t^{\prime}$
, where one considers t
′ to be a ‘large’ constant, we have
$t \geq t^{\prime}$
, where one considers t
′ to be a ‘large’ constant, we have
![]() $\mathcal{Z}_t = \alpha t$
, and for all
$\mathcal{Z}_t = \alpha t$
, and for all
![]() $k \in \mathbb{N}_{0}$
we have
$k \in \mathbb{N}_{0}$
we have
![]() $N_{k}(t, \{w\}) = {{\mathbb{E}\!\left[{N_{k}(t, \{w\})} \right]}} = \ell t \cdot n_{k}(\{w\})$
for some value
$N_{k}(t, \{w\}) = {{\mathbb{E}\!\left[{N_{k}(t, \{w\})} \right]}} = \ell t \cdot n_{k}(\{w\})$
for some value
![]() $n_{k}(\{w\})$
. The latter assumptions are motivated by the intuition that the respective quantities obey strong laws of large numbers. Then, for
$n_{k}(\{w\})$
. The latter assumptions are motivated by the intuition that the respective quantities obey strong laws of large numbers. Then, for
![]() $t \geq t^{\prime}$
and
$t \geq t^{\prime}$
and
![]() $k \geq 1$
, we have
$k \geq 1$
, we have
 \begin{align*}\ell n_{k}(\{w\}) & = {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{N_{k}(t+1, \{w\}) - N_{k}(t, \{w\})|\mathcal{T}_{t}} \right]}}} \right]}}\\ &= {{\mathbb{P}\!\left({\text{vertex of out-degree $\textit{k}$ and weight $\textit{w}$ chosen}}\right)}} \\ & \qquad\qquad\qquad - {{\mathbb{P} \!\left({\text{vertex of out-degree $k-1$ and weight $\textit{w}$ chosen}}\right)}}\\ &= N_{k-1}(t, \{w\}) \cdot \frac{f(k-1, w)}{{\mathcal{Z}}_t} - N_{k}(t, \{w\}) \cdot \frac{f(k,w)}{{\mathcal{Z}}_t}\\ &= \frac{\ell n_{k-1}(\{w\})\cdot f(k-1,w)}{\alpha} - \frac{\ell n_{k}(\{w\})\cdot f(k,w)}{\alpha}.\end{align*}
\begin{align*}\ell n_{k}(\{w\}) & = {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{N_{k}(t+1, \{w\}) - N_{k}(t, \{w\})|\mathcal{T}_{t}} \right]}}} \right]}}\\ &= {{\mathbb{P}\!\left({\text{vertex of out-degree $\textit{k}$ and weight $\textit{w}$ chosen}}\right)}} \\ & \qquad\qquad\qquad - {{\mathbb{P} \!\left({\text{vertex of out-degree $k-1$ and weight $\textit{w}$ chosen}}\right)}}\\ &= N_{k-1}(t, \{w\}) \cdot \frac{f(k-1, w)}{{\mathcal{Z}}_t} - N_{k}(t, \{w\}) \cdot \frac{f(k,w)}{{\mathcal{Z}}_t}\\ &= \frac{\ell n_{k-1}(\{w\})\cdot f(k-1,w)}{\alpha} - \frac{\ell n_{k}(\{w\})\cdot f(k,w)}{\alpha}.\end{align*}
Meanwhile, for
![]() $k =0$
we have
$k =0$
we have
 \begin{align*}\ell n_{0}(\{w\}) & = {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{N_{0}(t+1, \{w\}) - N_{0}(t, \{w\})|\mathcal{T}_{t}} \right]}}} \right]}}\\ &= {{\mathbb{P}\!\left({\text{newly arriving vertex with weight $\textit{w}$}}\right)}} \\ & \qquad\qquad\qquad - {{\mathbb{P} \!\left({\text{vertex of out-degree 0 and weight $\textit{w}$ chosen}} \right)}}\\ &= \ell \mu(\{w\}) - N_{0}(t, \{w\}) \cdot \frac{f(0,w)}{{\mathcal{Z}}_t}\\ &= \ell \mu(\{w\}) - \frac{\ell n_{0}(\{w\}) \cdot f(0,w)}{\alpha}.\end{align*}
\begin{align*}\ell n_{0}(\{w\}) & = {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{N_{0}(t+1, \{w\}) - N_{0}(t, \{w\})|\mathcal{T}_{t}} \right]}}} \right]}}\\ &= {{\mathbb{P}\!\left({\text{newly arriving vertex with weight $\textit{w}$}}\right)}} \\ & \qquad\qquad\qquad - {{\mathbb{P} \!\left({\text{vertex of out-degree 0 and weight $\textit{w}$ chosen}} \right)}}\\ &= \ell \mu(\{w\}) - N_{0}(t, \{w\}) \cdot \frac{f(0,w)}{{\mathcal{Z}}_t}\\ &= \ell \mu(\{w\}) - \frac{\ell n_{0}(\{w\}) \cdot f(0,w)}{\alpha}.\end{align*}
Solving the recursion from the above two displays, for all
![]() $k \in \mathbb{N}_0$
we have
$k \in \mathbb{N}_0$
we have
 \begin{align*}n_{k}(\{w\}) & = \mu(\{w\}) \cdot \frac{\alpha}{f(k, w) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,w)}{f(i,w) + \alpha}\\ & = {{\mathbb{E}\!\left[{\frac{\alpha}{f(k, W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}\mathbf{1}_{\{w\}}(W)} \right]}}.\end{align*}
\begin{align*}n_{k}(\{w\}) & = \mu(\{w\}) \cdot \frac{\alpha}{f(k, w) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,w)}{f(i,w) + \alpha}\\ & = {{\mathbb{E}\!\left[{\frac{\alpha}{f(k, W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}\mathbf{1}_{\{w\}}(W)} \right]}}.\end{align*}
It is therefore reasonable to expect that the limit of
![]() $\frac{N_{k}(t,B)}{\ell t}$
belongs to a one-parameter family
$\frac{N_{k}(t,B)}{\ell t}$
belongs to a one-parameter family
![]() $p^{\lambda}_{k}({\cdot})$
indexed by a positive real number
$p^{\lambda}_{k}({\cdot})$
indexed by a positive real number
![]() $\lambda$
such that
$\lambda$
such that
 \begin{equation} p^{\lambda}_{k}(B) \,:\!=\, {{\mathbb{E}\!\left[{\frac{\lambda}{f(k,W) + \lambda} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \lambda} \mathbf{1}_{B}(W)}\right]}},\end{equation}
\begin{equation} p^{\lambda}_{k}(B) \,:\!=\, {{\mathbb{E}\!\left[{\frac{\lambda}{f(k,W) + \lambda} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \lambda} \mathbf{1}_{B}(W)}\right]}},\end{equation}
where the parameter
![]() $\lambda$
can be recovered by the asymptotics of the partition function, so that the limit satisfies
$\lambda$
can be recovered by the asymptotics of the partition function, so that the limit satisfies
![]() $\lambda = \alpha > 0$
. It is important to note that in this paper, it may be the case that the limit of
$\lambda = \alpha > 0$
. It is important to note that in this paper, it may be the case that the limit of
![]() $\frac{N_{k}(t,B)}{\ell t}$
belongs to this family, but we do not necessarily have a strong law for the asymptotics of the partition function. For example, this is the case if the conditions of Theorem 2.1 are satisfied, but not those of Theorem 2.4.
$\frac{N_{k}(t,B)}{\ell t}$
belongs to this family, but we do not necessarily have a strong law for the asymptotics of the partition function. For example, this is the case if the conditions of Theorem 2.1 are satisfied, but not those of Theorem 2.4.
Now, note that for every
![]() $t \in \mathbb{N}_0$
, by computing the number of directed edges (v, v
′) in
$t \in \mathbb{N}_0$
, by computing the number of directed edges (v, v
′) in
![]() ${\mathcal{T}}_{t}$
with
${\mathcal{T}}_{t}$
with
![]() $W_v \in B$
in two different ways, we have
$W_v \in B$
in two different ways, we have
When we normalise by
![]() $\ell t$
, if, for
$\ell t$
, if, for
![]() $k \in \mathbb{N}_0$
the limit of
$k \in \mathbb{N}_0$
the limit of
![]() $\frac{N_{k}(t,B)}{\ell t}$
is
$\frac{N_{k}(t,B)}{\ell t}$
is
![]() $p^{\alpha}_{k}(B)$
, by Fatou’s lemma we get
$p^{\alpha}_{k}(B)$
, by Fatou’s lemma we get
which motivates the definition of the following family indexed by a positive real number
![]() $\lambda$
:
$\lambda$
:
 \begin{equation} m(\lambda,B) \,:\!=\, \sum_{k=0}^{\infty} \ell k p^{\lambda}_{k}(B) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,W)}{f(i,W) + \lambda} \mathbf{1}_{B}(W)} \right]}}.\end{equation}
\begin{equation} m(\lambda,B) \,:\!=\, \sum_{k=0}^{\infty} \ell k p^{\lambda}_{k}(B) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,W)}{f(i,W) + \lambda} \mathbf{1}_{B}(W)} \right]}}.\end{equation}
Now, if the limit exists, since we add
![]() $\ell$
edges at each time-step, the limits of the measures
$\ell$
edges at each time-step, the limits of the measures
![]() $\Xi(t, \cdot)/\ell t$
are probability measures. However, if
$\Xi(t, \cdot)/\ell t$
are probability measures. However, if
![]() $m(\alpha,\cdot)$
is not a probability distribution, we can show that there exists a measurable set B such that
$m(\alpha,\cdot)$
is not a probability distribution, we can show that there exists a measurable set B such that
In this case, the inequality in (5) is strict, so that, after normalising by
![]() $\ell t$
, the operations of taking limits in k and in t in (4) do not commute. Thus, the set B has acquired additional ‘mass’ in the limit. We call this phenomenon condensation, motivated by the term used in the network science literature (e.g. [Reference Bianconi and Barabási5]). In Section 3.2 we derive an example of this in the case that
$\ell t$
, the operations of taking limits in k and in t in (4) do not commute. Thus, the set B has acquired additional ‘mass’ in the limit. We call this phenomenon condensation, motivated by the term used in the network science literature (e.g. [Reference Bianconi and Barabási5]). In Section 3.2 we derive an example of this in the case that
![]() $f(i,W) = g(W)i + h(W)$
, where g is bounded. This generalises the case
$f(i,W) = g(W)i + h(W)$
, where g is bounded. This generalises the case
![]() $f(i,W) = (i+1)W$
which has already been studied in [Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich, Mailler and Mörters12, Reference Dereich and Ortgiese14] under the name preferential attachment with multiplicative fitness.
$f(i,W) = (i+1)W$
which has already been studied in [Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich, Mailler and Mörters12, Reference Dereich and Ortgiese14] under the name preferential attachment with multiplicative fitness.
1.4. Open problems
The discussion in Section 1.3 shows that much of the analysis of this model depends on a parameter
![]() $\alpha$
. We conjecture that, in general, this parameter makes
$\alpha$
. We conjecture that, in general, this parameter makes
![]() $m(\lambda, \cdot)$
‘as close as possible’ to a probability distribution, so that
$m(\lambda, \cdot)$
‘as close as possible’ to a probability distribution, so that
where we follow the convention that
![]() $\inf{\varnothing} = \infty$
.
$\inf{\varnothing} = \infty$
.
Conjecture 1.1. Let
![]() ${\mathcal{T}}$
be a
${\mathcal{T}}$
be a
![]() ${\left({\mu, f, \ell}\right)}$
-RIF tree, with
${\left({\mu, f, \ell}\right)}$
-RIF tree, with
![]() $\alpha$
as defined in (7). Then, for each
$\alpha$
as defined in (7). Then, for each
![]() $k \in \mathbb{N}_0$
and measurable set B, almost surely, we have
$k \in \mathbb{N}_0$
and measurable set B, almost surely, we have
 \begin{equation*}\frac{N_{k}(t, B)}{\ell t} \xrightarrow{t \to \infty}\begin{cases}p^{\alpha}_{k}(B) & if\ \alpha < \infty, \\[5pt]\mu(B)\mathbf{1}_{\{0\}}(k) & {otherwise}.\end{cases}\end{equation*}
\begin{equation*}\frac{N_{k}(t, B)}{\ell t} \xrightarrow{t \to \infty}\begin{cases}p^{\alpha}_{k}(B) & if\ \alpha < \infty, \\[5pt]\mu(B)\mathbf{1}_{\{0\}}(k) & {otherwise}.\end{cases}\end{equation*}
The conjectured limit in the case when
![]() $\alpha = \infty$
is obtained by taking the limit of
$\alpha = \infty$
is obtained by taking the limit of
![]() $p^{\alpha}_{k}(B)$
as
$p^{\alpha}_{k}(B)$
as
![]() $\alpha \to \infty$
. This limit is 0 unless
$\alpha \to \infty$
. This limit is 0 unless
![]() $k = 0$
, in which case it is
$k = 0$
, in which case it is
![]() $\mu(B)$
.
$\mu(B)$
.
Remark 1.3. Conjecture 1.1 has a natural analogue in the setting, as in Remark 1.2, that the sequence
![]() $(f(k,W))_{k \in \mathbb{N}_{0}}$
is instead given by a general stochastic process indexed by
$(f(k,W))_{k \in \mathbb{N}_{0}}$
is instead given by a general stochastic process indexed by
![]() $\mathbb{N}_{0}$
, depending on an initial source of randomness W. In this case, the expectation in (3) is instead taken over evolution over all sequences, with initial
$\mathbb{N}_{0}$
, depending on an initial source of randomness W. In this case, the expectation in (3) is instead taken over evolution over all sequences, with initial
![]() $W \in B$
. The techniques used in this paper translate without modification to this case, the only important feature being that the sequences corresponding to different vertices are independent of each other.
$W \in B$
. The techniques used in this paper translate without modification to this case, the only important feature being that the sequences corresponding to different vertices are independent of each other.
Remark 1.4. It is important to note the order of the quantifiers in Conjecture 1.1: given a sequence
![]() $(\mu_{j})_{j \in \mathbb{N}}$
of random measures on
$(\mu_{j})_{j \in \mathbb{N}}$
of random measures on
![]() $\mathbb{R}_{+}$
, we have that, for any measurable set B,
$\mathbb{R}_{+}$
, we have that, for any measurable set B,
![]() $\lim_{j \to \infty} \mu_{j}(B) = \mu_{\infty}(B)$
almost surely; it is not necessarily the case that, almost surely, for all measurable sets B we have
$\lim_{j \to \infty} \mu_{j}(B) = \mu_{\infty}(B)$
almost surely; it is not necessarily the case that, almost surely, for all measurable sets B we have
![]() $\lim_{j \to \infty} \mu_{j}(B) = \mu_{\infty}(B)$
. However, it is the case that almost surely,
$\lim_{j \to \infty} \mu_{j}(B) = \mu_{\infty}(B)$
. However, it is the case that almost surely,
![]() $\mu_{j} \rightarrow \mu_{\infty}$
in the weak topology. This uses the fact that there exists a countable family of measurable sets such that any open set in
$\mu_{j} \rightarrow \mu_{\infty}$
in the weak topology. This uses the fact that there exists a countable family of measurable sets such that any open set in
![]() $\mathbb{R}_{+}$
may be expressed as a disjoint, countable union of elements of this family. For example, one may take the set of all dyadic intervals, with endpoints of the form
$\mathbb{R}_{+}$
may be expressed as a disjoint, countable union of elements of this family. For example, one may take the set of all dyadic intervals, with endpoints of the form
![]() $j \cdot 2^{-n}$
,
$j \cdot 2^{-n}$
,
![]() $(j+1) \cdot 2^{-n}$
, where
$(j+1) \cdot 2^{-n}$
, where
![]() $j, n \in \mathbb{N}_{0}$
, and then apply the portmanteau theorem. This approach is also used in this paper in the proof of Corollary 3.1.
$j, n \in \mathbb{N}_{0}$
, and then apply the portmanteau theorem. This approach is also used in this paper in the proof of Corollary 3.1.
The discussion in Section 1.3 described the quantity
![]() $\alpha$
as being closely related to the partition function. As a result, we also conjecture the following.
$\alpha$
as being closely related to the partition function. As a result, we also conjecture the following.
Conjecture 1.2. Let
![]() ${\mathcal{T}}$
be a
${\mathcal{T}}$
be a
![]() ${\left({\mu, f, \ell}\right)}$
-RIF tree, with
${\left({\mu, f, \ell}\right)}$
-RIF tree, with
![]() $\alpha$
as defined in (7). Then we have
$\alpha$
as defined in (7). Then we have
1.5. Important technical conditions and overview of results
In this paper, we make partial progress towards the proofs of Conjecture 1.1 and Conjecture 1.2. We will refer to the following technical conditions:
-
C1 With
 $m(\lambda, \cdot)$
as defined in (6), there exists some
$m(\lambda, \cdot)$
as defined in (6), there exists some
 $\lambda > 0$
such that (8)Under this condition, by monotonicity, there exists a unique
$\lambda > 0$
such that (8)Under this condition, by monotonicity, there exists a unique \begin{equation} 1 < m(\lambda, \mathbb{R}_{+}) < \infty.\end{equation}
\begin{equation} 1 < m(\lambda, \mathbb{R}_{+}) < \infty.\end{equation}
 $\alpha > 0$
such that
$\alpha > 0$
such that
 $m(\alpha, \mathbb{R}_{+}) = 1$
; we call this the Malthusian parameter associated with the process.
$m(\alpha, \mathbb{R}_{+}) = 1$
; we call this the Malthusian parameter associated with the process.
-
C2 There exists
 $\alpha > 0$
such that
$\alpha > 0$
such that  \begin{equation*} \lim_{t \to \infty} \frac{{\mathcal{Z}}_t}{t} = \alpha.\end{equation*}
\begin{equation*} \lim_{t \to \infty} \frac{{\mathcal{Z}}_t}{t} = \alpha.\end{equation*}
Note that in (7) and in Conditions C1 and C2 we use the same symbol
![]() $\alpha$
. This these coincide in general. In general, as we only assume either C1 or C2 at a time, the definition will be clear from context.
$\alpha$
. This these coincide in general. In general, as we only assume either C1 or C2 at a time, the definition will be clear from context.
The paper will be structured as follows.
Section 2: We analyse the model under Condition C1.
In Theorem 2.1 we prove Conjecture 1.1 under Condition C1, and as a consequence, in Theorem 2.2 we show that, for any measurable set B,
 $\Xi(t,B)/\ell t$
converges almost surely to
$\Xi(t,B)/\ell t$
converges almost surely to
 $m(\alpha, B)$
.
$m(\alpha, B)$
.In Theorem 2.4 we derive a condition under which C1 implies C2. In particular, this proves Conjecture 1.2 under this condition and C1.
The approaches used in this section are well established, applying classical results in the theory of Crump–Mode–Jagers branching processes, in a similar manner to the approaches taken by the authors of [Reference Bhamidi3, Reference Dereich, Mailler and Mörters12, Reference Holmgren and Janson20, Reference Rudas, Tóth and Valkó33]. Nevertheless, these theorems have novel applications: we apply the theorems to the evolving Cayley tree considered by Bianconi in Example 2.4.1 and the weighted random recursive tree.
Section 3: We analyse a particular case of the model when the fitness function is such that
![]() $f(i,W) = g(W)i + h(W)$
, which we call the generalised preferential attachment tree with fitness (GPAF-tree). This extends the existing models of preferential attachment with additive fitness, i.e.,
$f(i,W) = g(W)i + h(W)$
, which we call the generalised preferential attachment tree with fitness (GPAF-tree). This extends the existing models of preferential attachment with additive fitness, i.e.,
![]() $f(i,W) = i + 1 + W$
, and multiplicative fitness, i.e.,
$f(i,W) = i + 1 + W$
, and multiplicative fitness, i.e.,
![]() $f(i,W) = (i+1)W$
. When the function g is non-decreasing, we also treat the cases where Condition C1 can fail. Let
$f(i,W) = (i+1)W$
. When the function g is non-decreasing, we also treat the cases where Condition C1 can fail. Let
![]() $\alpha$
be as defined in (7), and also define
$\alpha$
be as defined in (7), and also define
![]() $\Lambda \,:\!=\, \left\{\lambda > 0\,:\, m(\lambda, \mathbb{R}_{+}) < \infty \right\}$
.
$\Lambda \,:\!=\, \left\{\lambda > 0\,:\, m(\lambda, \mathbb{R}_{+}) < \infty \right\}$
.
We consider the situation in which Condition C1 fails by having
 $m(\lambda,\mathbb{R}_{+}) \leq 1$
for all
$m(\lambda,\mathbb{R}_{+}) \leq 1$
for all
 $\lambda \in \Lambda$
. In this case,
$\lambda \in \Lambda$
. In this case,
 $m(\lambda, \mathbb{R}_{+})$
is finite for some
$m(\lambda, \mathbb{R}_{+})$
is finite for some
 $\lambda > 0$
, but never exceeds 1, so that
$\lambda > 0$
, but never exceeds 1, so that
 $m(\alpha, \mathbb{R}_{+}) \leq 1$
. In Theorem 3.1 we prove Conjecture 1.1 and Conjecture 1.2 in this case, showing, in particular, that if
$m(\alpha, \mathbb{R}_{+}) \leq 1$
. In Theorem 3.1 we prove Conjecture 1.1 and Conjecture 1.2 in this case, showing, in particular, that if
 $m(\alpha, \mathbb{R}_{+}) < 1$
the GPAF-tree exhibits a condensation phenomenon.
$m(\alpha, \mathbb{R}_{+}) < 1$
the GPAF-tree exhibits a condensation phenomenon.Alternatively, Condition C1 may fail by having
 $\alpha = \infty$
. Theorem 3.2 also confirms Conjecture 1.1 in this case, showing that the limiting degree distribution is degenerate: almost surely the proportion of leaves in the tree tends to 1. Moreover, we show that the fittest take all of the mass of the distribution of edges according to weight, in the sense that a proportion of edges tending to 1 accumulates around the sets of vertices with weights conferring higher and higher fitness.
$\alpha = \infty$
. Theorem 3.2 also confirms Conjecture 1.1 in this case, showing that the limiting degree distribution is degenerate: almost surely the proportion of leaves in the tree tends to 1. Moreover, we show that the fittest take all of the mass of the distribution of edges according to weight, in the sense that a proportion of edges tending to 1 accumulates around the sets of vertices with weights conferring higher and higher fitness.The techniques in this section are inspired by the coupling techniques exploited in [Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich, Mailler and Mörters12], and extend the well-known phase transition associated with the model of preferential attachment with multiplicative fitnesses studied in [Reference Borgs, Chayes, Daskalakis and Roch8, Reference Dereich, Mailler and Mörters12, Reference Dereich and Ortgiese14]. This generalisation shows that the phase transition depends on the parameter h too, so that, in some circumstances, condensation occurs, but vanishes if h is increased enough pointwise (see Section 3.2.2). This is interesting because h(W) may be interpreted as the ‘initial’ popularity of a vertex when it arrives in the tree, showing that in order for the condensation to occur, there need to be sufficiently many vertices of ‘low enough’ initial popularity. As far as the author is aware, these results are novel not only in the mathematical literature, but also in the general scientific literature concerning complex networks.
Section 4: We analyse the model under Condition C2, proving general results for the distribution of vertices with a given degree and weight.
If the term
 $\alpha$
in Condition C2 is finite, Theorem 4.1 and Theorem 4.2 confirm a weaker analogue of Conjecture 1.1 under this condition.
$\alpha$
in Condition C2 is finite, Theorem 4.1 and Theorem 4.2 confirm a weaker analogue of Conjecture 1.1 under this condition.The techniques used in this section are similar to those used in the proof of [Reference Fountoulakis, Iyer, Mailler and Sulzbach17, Theorem 6]; however, in this instance we present a considerably shorter proof.
2. Analysis of
 $\left({\mu, f, \ell}\right)$
-RIF trees assuming C1
$\left({\mu, f, \ell}\right)$
-RIF trees assuming C1
In order to apply Condition C1 in this section, we study a branching process with a family tree made up of individuals and their offspring whose distribution is identical to the discrete-time model at the times of the branching events. In Section 2.1, we describe this continuous-time model, state Theorem 2.1, and state and prove Theorem 2.2. In Section 2.2 we include the relevant theory of Crump–Mode–Jagers branching processes and use this to prove Theorem 2.1. In Section 2.3 we apply the same theory, along with some technical lemmas, to state and prove a strong law of large numbers for the partition function in Theorem 2.4. We conclude the section with some interesting examples in Section 2.4.
2.1. Description of continuous-time embedding
In the continuous-time approach, we begin with a population consisting of a single vertex 0 with weight
![]() $W_0$
sampled from
$W_0$
sampled from
![]() $\mu$
and an associated exponential clock with parameter
$\mu$
and an associated exponential clock with parameter
![]() $f(0,W_0)$
. Then recursively, when the ith birth event occurs in the population, with the ringing of an exponential clock associated to vertex j, the following occurs:
$f(0,W_0)$
. Then recursively, when the ith birth event occurs in the population, with the ringing of an exponential clock associated to vertex j, the following occurs:
-
(i) Vertex j produces offspring
 $\ell (i-1) + 1, \ldots, \ell i$
with independent weights
$\ell (i-1) + 1, \ldots, \ell i$
with independent weights
 $W_{\ell (i-1) +1}, \ldots, W_{\ell i}$
sampled from
$W_{\ell (i-1) +1}, \ldots, W_{\ell i}$
sampled from
 $\mu$
and exponential clocks with parameters
$\mu$
and exponential clocks with parameters
 $f(0, W_{\ell (i-1) +1}), \ldots, f(0, W_{\ell i})$
.
$f(0, W_{\ell (i-1) +1}), \ldots, f(0, W_{\ell i})$
. -
(ii) Suppose the number of offspring of j before the birth event was m, so that its out-degree in the family tree is m. Then the exponential random variable associated with j is updated to have rate
 $f(m/\ell + 1, {W_{j}})$
. If
$f(m/\ell + 1, {W_{j}})$
. If
 $f(m/\ell + 1, {W_{j}}) = 0$
, then j ceases to produce offspring and we say j has died.
$f(m/\ell + 1, {W_{j}}) = 0$
, then j ceases to produce offspring and we say j has died.
Now, if we let
![]() ${\mathcal{Z}}_{i-1}$
denote the sum of the rates of the exponential clocks in the population when the population has size
${\mathcal{Z}}_{i-1}$
denote the sum of the rates of the exponential clocks in the population when the population has size
![]() $i-1$
, the probability that the clock associated with j is the first to ring is
$i-1$
, the probability that the clock associated with j is the first to ring is
![]() $f(m/\ell, W_j)/{\mathcal{Z}}_{i-1}$
. Hence, the family tree of the continuous-time model at the times of the birth events
$f(m/\ell, W_j)/{\mathcal{Z}}_{i-1}$
. Hence, the family tree of the continuous-time model at the times of the birth events
![]() $(\sigma_{i})_{i \geq 0}$
has the same distribution as the associated
$(\sigma_{i})_{i \geq 0}$
has the same distribution as the associated
![]() ${\left({\mu, f, \ell}\right)}$
-RIF tree. The continuous-time branching process is actually a Crump–Mode–Jagers branching process, which we will describe in more depth in Section 2.2.
${\left({\mu, f, \ell}\right)}$
-RIF tree. The continuous-time branching process is actually a Crump–Mode–Jagers branching process, which we will describe in more depth in Section 2.2.
To describe the evolution of the degree of a vertex in the continuous-time model, we define the pure birth process with underlying probability space
![]() $(\Omega, \mathcal{F}, \mathbb{P})$
and state space
$(\Omega, \mathcal{F}, \mathbb{P})$
and state space
![]() $\ell \mathbb{N}$
as follows. First sample a weight W and set
$\ell \mathbb{N}$
as follows. First sample a weight W and set
![]() $Y(0) = 0$
. Let
$Y(0) = 0$
. Let
![]() $\mathbb{P}_{w}$
denote the probability measure associated with the process when the weight sampled is w. Then define the birth rates of Y so that
$\mathbb{P}_{w}$
denote the probability measure associated with the process when the weight sampled is w. Then define the birth rates of Y so that
In other words, the time taken to jump from
![]() $k\ell$
to
$k\ell$
to
![]() $(k + 1)\ell$
is exponentially distributed with parameter f(k, w).
$(k + 1)\ell$
is exponentially distributed with parameter f(k, w).
Let
![]() $\rho$
denote the point process corresponding to the jumps in Y, and denote by
$\rho$
denote the point process corresponding to the jumps in Y, and denote by
![]() ${{\mathbb{E}_{w} \!\left[{\rho({\cdot})} \right]}}$
the intensity measure when the weight
${{\mathbb{E}_{w} \!\left[{\rho({\cdot})} \right]}}$
the intensity measure when the weight
![]() $W = w$
. Also, denote by
$W = w$
. Also, denote by
![]() $\hat{\rho}_w$
the Laplace–Stieltjes transform, i.e.,
$\hat{\rho}_w$
the Laplace–Stieltjes transform, i.e.,
Note that, by Fubini’s theorem, we have
 \begin{align} \hat{\rho}_w(\lambda) & = \int_{0}^{\infty} \left(\int_{t}^{\infty} \lambda e^{- \lambda s} {\text{d}} s \right)\, {{\mathbb{E}_{w} \!\left[{\rho({\text{d}} t)} \right]}} & =\int_{0}^{\infty} \lambda e^{-\lambda s} \left(\int_{0}^{s} {{\mathbb{E}_{w} \!\left[{\rho({\text{d}} t)} \right]}}\right) {\text{d}} s\\ & = \int_{0}^{\infty} \lambda e^{-\lambda s} {{\mathbb{E}_{w} \!\left[{Y(s)} \right]}}{\text{d}} s. \nonumber \end{align}
\begin{align} \hat{\rho}_w(\lambda) & = \int_{0}^{\infty} \left(\int_{t}^{\infty} \lambda e^{- \lambda s} {\text{d}} s \right)\, {{\mathbb{E}_{w} \!\left[{\rho({\text{d}} t)} \right]}} & =\int_{0}^{\infty} \lambda e^{-\lambda s} \left(\int_{0}^{s} {{\mathbb{E}_{w} \!\left[{\rho({\text{d}} t)} \right]}}\right) {\text{d}} s\\ & = \int_{0}^{\infty} \lambda e^{-\lambda s} {{\mathbb{E}_{w} \!\left[{Y(s)} \right]}}{\text{d}} s. \nonumber \end{align}
Moreover, if we write
![]() $\tau_{k}$
for the time of the kth jump in Y, we have
$\tau_{k}$
for the time of the kth jump in Y, we have
![]() $\rho = \sum_{k=0}^{\infty} \ell \delta_{\tau_{k}}.$
Note that if the weight of Y is w, then
$\rho = \sum_{k=0}^{\infty} \ell \delta_{\tau_{k}}.$
Note that if the weight of Y is w, then
![]() $\tau_{k}$
is distributed as a sum of independent exponentially distributed random variables with rates
$\tau_{k}$
is distributed as a sum of independent exponentially distributed random variables with rates
![]() $f(0,w), f(1,w), \ldots, f(k-1,w)$
, where we follow the convention that an exponentially distributed random variable with rate 0 is
$f(0,w), f(1,w), \ldots, f(k-1,w)$
, where we follow the convention that an exponentially distributed random variable with rate 0 is
![]() $\infty$
. Thus, we have that
$\infty$
. Thus, we have that
 \begin{equation} \hat{\rho}_w(\lambda) = \ell \sum_{n=1}^{\infty} {{\mathbb{E}_{w} \!\left[{e^{-\lambda \tau_{n}}} \right]}} =\ell\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,w)}{f(i,w) + \lambda},\end{equation}
\begin{equation} \hat{\rho}_w(\lambda) = \ell \sum_{n=1}^{\infty} {{\mathbb{E}_{w} \!\left[{e^{-\lambda \tau_{n}}} \right]}} =\ell\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,w)}{f(i,w) + \lambda},\end{equation}
where in the last equality we have used the facts that a Laplace–Stieltjes transform of a convolution of measures is the product of Laplace–Stieltjes transforms, and the Laplace–Stieltjes transform
![]() $\hat{X}(\lambda)$
of an exponentially distributed random variable with parameter s is
$\hat{X}(\lambda)$
of an exponentially distributed random variable with parameter s is
![]() $\int_{0}^{\infty} e^{-\lambda t} s e^{- s t} {\text{d}} t = \frac{s}{s+\lambda}$
. Therefore, we see that
$\int_{0}^{\infty} e^{-\lambda t} s e^{- s t} {\text{d}} t = \frac{s}{s+\lambda}$
. Therefore, we see that
![]() ${{\mathbb{E} \!\left[{\hat{\rho}_{W}(\lambda)} \right]}} = m(\lambda, \mathbb{R}_{+})$
as defined in (8), and Condition C1 implies that there exists some
${{\mathbb{E} \!\left[{\hat{\rho}_{W}(\lambda)} \right]}} = m(\lambda, \mathbb{R}_{+})$
as defined in (8), and Condition C1 implies that there exists some
![]() $\lambda > 0$
such that
$\lambda > 0$
such that
![]() $1 < {{\mathbb{E}\!\left[{\hat{\rho}_{W}(\lambda)} \right]}} < \infty$
. In addition, the Malthusian parameter
$1 < {{\mathbb{E}\!\left[{\hat{\rho}_{W}(\lambda)} \right]}} < \infty$
. In addition, the Malthusian parameter
![]() $\alpha$
appearing in Condition C1 is the unique positive real number such that
$\alpha$
appearing in Condition C1 is the unique positive real number such that
 \begin{equation} {{\mathbb{E}\!\left[{\hat{\rho}_{W}(\alpha)} \right]}} = m(\alpha, \mathbb{R}_{+}) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}} = 1.\end{equation}
\begin{equation} {{\mathbb{E}\!\left[{\hat{\rho}_{W}(\alpha)} \right]}} = m(\alpha, \mathbb{R}_{+}) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}} = 1.\end{equation}
Our first result is the following.
Theorem 2.1. (Convergence of the degree distribution under C1.) Let
![]() ${\mathcal{T}}$
be a
${\mathcal{T}}$
be a
![]() ${{\left({\mu, f, \ell}\right)}}$
-RIF tree satisfying C1 with Malthusian parameter
${{\left({\mu, f, \ell}\right)}}$
-RIF tree satisfying C1 with Malthusian parameter
![]() $\alpha$
. Then, for any measurable set
$\alpha$
. Then, for any measurable set
![]() $B \subseteq \mathbb{R}_+$
, with
$B \subseteq \mathbb{R}_+$
, with
![]() $N_{k}(t, B)$
as defined in (1) and
$N_{k}(t, B)$
as defined in (1) and
![]() $p^{\alpha}_{k}(B)$
as defined in (3), we have
$p^{\alpha}_{k}(B)$
as defined in (3), we have
almost surely.
The limiting formula for Theorem 2.1 has appeared in a number of contexts, and generalises many known results. Under Condition C1 this result was proved by Rudas, Tóth and Valkó [Reference Rudas, Tóth and Valkó33] in the case that W is constant and
![]() $\ell = 1$
. The cases
$\ell = 1$
. The cases
![]() $f(i,W) = W(i+1)$
and
$f(i,W) = W(i+1)$
and
![]() $f(i,W) = i+1+W$
with
$f(i,W) = i+1+W$
with
![]() $\ell = 1$
correspond respectively to the preferential attachment models with multiplicative and additive fitness mentioned in the introduction. In the multiplicative model, the result was first proved in [Reference Borgs, Chayes, Daskalakis and Roch8] and later in [Reference Bhamidi3]. In [Reference Bhamidi3], Bhamidi also first proved the result for the case
$\ell = 1$
correspond respectively to the preferential attachment models with multiplicative and additive fitness mentioned in the introduction. In the multiplicative model, the result was first proved in [Reference Borgs, Chayes, Daskalakis and Roch8] and later in [Reference Bhamidi3]. In [Reference Bhamidi3], Bhamidi also first proved the result for the case
![]() $f(i,W) = i + 1 + W$
. These models are examples of the generalised preferential attachment tree with fitness, which we study in more depth in Section 3. Finally, the case
$f(i,W) = i + 1 + W$
. These models are examples of the generalised preferential attachment tree with fitness, which we study in more depth in Section 3. Finally, the case
![]() $f(i,W) = W$
,
$f(i,W) = W$
,
![]() $\ell = 1$
corresponds to a model of weighted random recursive trees (see Example 2.4.2). We postpone the proof of Theorem 2.1 to the end of Section 2.2.
$\ell = 1$
corresponds to a model of weighted random recursive trees (see Example 2.4.2). We postpone the proof of Theorem 2.1 to the end of Section 2.2.
Remark 2.1. The limiting value has an interesting interpretation as a generalised geometric distribution. Consider an experiment where W is sampled from
![]() $\mu$
and, given W, coins are flipped, where the probability of heads in the ith coin flip is proportional to f(i,W) and tails proportional to
$\mu$
and, given W, coins are flipped, where the probability of heads in the ith coin flip is proportional to f(i,W) and tails proportional to
![]() $\alpha$
. Then the limiting distribution in Theorem 2.1 is the distribution of first occurrence of tails. Note that, by C1, the C1, the probability of infinite sequences of heads is 0.
$\alpha$
. Then the limiting distribution in Theorem 2.1 is the distribution of first occurrence of tails. Note that, by C1, the C1, the probability of infinite sequences of heads is 0.
Remark 2.2. Note that
![]() $Y(t) < \infty$
for all
$Y(t) < \infty$
for all
![]() $t \geq 0$
almost surely if
$t \geq 0$
almost surely if
![]() $\tau_{\infty} \,:\!=\, \lim_{k \to \infty} \tau_{k} = \infty$
almost surely. The latter is satisfied if there exists
$\tau_{\infty} \,:\!=\, \lim_{k \to \infty} \tau_{k} = \infty$
almost surely. The latter is satisfied if there exists
![]() $\lambda > 0 $
such that for almost all w
$\lambda > 0 $
such that for almost all w
which is implied by C1. In the literature concerning pure birth Markov chains, this property is known as non-explosivity.
Remark 2.3. In this paper, we have considered the case where the function f, and thus the birth process Y as defined in (9), depends on a single random variable W taking values in
![]() $\mathbb{R}_{+}$
. However, there is no loss of generality in assuming the random variable W takes values in an arbitrary measure space, so long as the function f is measurable. In particular, we may consider the case where the weight is given by a vector
$\mathbb{R}_{+}$
. However, there is no loss of generality in assuming the random variable W takes values in an arbitrary measure space, so long as the function f is measurable. In particular, we may consider the case where the weight is given by a vector
![]() $(W_1,W_2)$
where
$(W_1,W_2)$
where
![]() $W_1$
and
$W_1$
and
![]() $W_2$
are possibly correlated random variables.
$W_2$
are possibly correlated random variables.
Now, recall the definitions of
![]() $\Xi(t, \cdot)$
from (2) and
$\Xi(t, \cdot)$
from (2) and
![]() $m(\alpha, \cdot)$
from (6). In the case that
$m(\alpha, \cdot)$
from (6). In the case that
![]() $m(\alpha, \cdot)$
is a probability distribution, the almost sure convergence of
$m(\alpha, \cdot)$
is a probability distribution, the almost sure convergence of
![]() $N_{k}(t,B)/\ell n$
to
$N_{k}(t,B)/\ell n$
to
![]() $p^{\alpha}_{k}(B)$
for any measurable set B is enough to imply that for any measurable set B the quantity
$p^{\alpha}_{k}(B)$
for any measurable set B is enough to imply that for any measurable set B the quantity
![]() $\Xi(t,B)$
converges almost surely to
$\Xi(t,B)$
converges almost surely to
![]() $m(\alpha, B)$
. Note that this condition is weaker than directly assuming C1. In particular, we have the following.
$m(\alpha, B)$
. Note that this condition is weaker than directly assuming C1. In particular, we have the following.
Theorem 2.2. Assume
![]() ${\mathcal{T}}$
is a
${\mathcal{T}}$
is a
![]() ${\left({\mu,f, \ell}\right)}$
-RIF tree with limiting degree distribution of the form
${\left({\mu,f, \ell}\right)}$
-RIF tree with limiting degree distribution of the form
![]() $(p^{\alpha}_{k}({\cdot}))_{k \in \mathbb{N}_{0}}$
and such that
$(p^{\alpha}_{k}({\cdot}))_{k \in \mathbb{N}_{0}}$
and such that
![]() $m(\alpha, \mathbb{R}_{+}) = 1$
. Then for any measurable set B we have
$m(\alpha, \mathbb{R}_{+}) = 1$
. Then for any measurable set B we have
almost surely.
To prove this theorem, we will apply the following elementary bound: for any two sequences
![]() $(a_n)_{n \in \mathbb{N}}$
,
$(a_n)_{n \in \mathbb{N}}$
,
![]() $(b_{n})_{n \in \mathbb{N}}$
such that either
$(b_{n})_{n \in \mathbb{N}}$
such that either
![]() $\liminf_{n \to \infty} a_n > -\infty$
or
$\liminf_{n \to \infty} a_n > -\infty$
or
![]() $\limsup_{n \to \infty} b_n < \infty$
, we have
$\limsup_{n \to \infty} b_n < \infty$
, we have
Proof of Theorem
2.2. Recall that, by (4), for each t, we have
![]() $\Xi(t,B) = \sum_{k=1}^{t} k \ell N_{k}(t,B)$
. Also note that
$\Xi(t,B) = \sum_{k=1}^{t} k \ell N_{k}(t,B)$
. Also note that
 \begin{align*}\sum_{k=0}^{\infty} k \ell p^{\alpha}_{k}(B)& = \ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} \frac{k\alpha}{f(k,W) + \alpha} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right) \mathbf{1}_{B}(W)} \right]}} \\ & = \ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} k \cdot \left(1 - \frac{f(k,W)}{f(k,W) + \alpha}\right) \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right) \mathbf{1}_{B}(W)} \right]}}\\ & = \ell \cdot {{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \left(k\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} - k\prod_{i=0}^{k} \frac{f(i,W)}{f(i,W) + \alpha}\right)\mathbf{1}_{B}(W)} \right]}} \\ & =\ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}\right) \mathbf{1}_{B}(W)} \right]}} = m(\alpha, B),\end{align*}
\begin{align*}\sum_{k=0}^{\infty} k \ell p^{\alpha}_{k}(B)& = \ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} \frac{k\alpha}{f(k,W) + \alpha} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right) \mathbf{1}_{B}(W)} \right]}} \\ & = \ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} k \cdot \left(1 - \frac{f(k,W)}{f(k,W) + \alpha}\right) \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right) \mathbf{1}_{B}(W)} \right]}}\\ & = \ell \cdot {{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \left(k\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} - k\prod_{i=0}^{k} \frac{f(i,W)}{f(i,W) + \alpha}\right)\mathbf{1}_{B}(W)} \right]}} \\ & =\ell \cdot {{\mathbb{E}\!\left[{\left(\sum_{k=1}^{\infty} \prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}\right) \mathbf{1}_{B}(W)} \right]}} = m(\alpha, B),\end{align*}
where the second-to-last equality follows from the telescoping nature of the sum inside the expectation. Thus, by Fatou’s lemma, almost surely we have
and likewise, almost surely,
![]() $\liminf_{t \to \infty} \frac{\Xi(t,B^c)}{\ell t} \geq m(\alpha, B^c)$
. Now, since we add
$\liminf_{t \to \infty} \frac{\Xi(t,B^c)}{\ell t} \geq m(\alpha, B^c)$
. Now, since we add
![]() $\ell$
edges at every time-step,
$\ell$
edges at every time-step,
![]() $\Xi(t,\mathbb{R}_{+}) = \ell t$
. Thus, by (13),
$\Xi(t,\mathbb{R}_{+}) = \ell t$
. Thus, by (13),
 \begin{align*}1 = \liminf_{t \to \infty} \left(\frac{\Xi(t, B)}{\ell t} + \frac{\Xi(t,B^{c})}{\ell t}\right)& \leq \liminf_{t \to \infty} \frac{\Xi(t, B^c)}{\ell t} + \limsup_{t \to \infty} \frac{\Xi(t,B)}{\ell t} \\ & \leq \limsup_{t \to \infty} \left(\frac{\Xi(t, B)}{\ell t} + \frac{\Xi(t,B^{c})}{\ell t}\right) = 1.\end{align*}
\begin{align*}1 = \liminf_{t \to \infty} \left(\frac{\Xi(t, B)}{\ell t} + \frac{\Xi(t,B^{c})}{\ell t}\right)& \leq \liminf_{t \to \infty} \frac{\Xi(t, B^c)}{\ell t} + \limsup_{t \to \infty} \frac{\Xi(t,B)}{\ell t} \\ & \leq \limsup_{t \to \infty} \left(\frac{\Xi(t, B)}{\ell t} + \frac{\Xi(t,B^{c})}{\ell t}\right) = 1.\end{align*}
But
![]() $m(\alpha, \cdot)$
is a probability measure; this is only possible if
$m(\alpha, \cdot)$
is a probability measure; this is only possible if
2.2. Crump–Mode–Jagers branching processes
In the continuous-time setting, it is convenient not only to identify individuals of the branching process according to the order in which they were born, but also to record their lineage, in such a way that the labelling encodes the structure of the tree. Therefore we also identify individuals of the branching process with elements of the infinite Ulam–Harris tree
![]() $\mathcal{U} \,:\!=\, \bigcup_{n \geq 0} \mathbb{N}^{n}$
, where
$\mathcal{U} \,:\!=\, \bigcup_{n \geq 0} \mathbb{N}^{n}$
, where
![]() $\mathbb{N}^{0} = \varnothing$
is the root. In this case, an individual
$\mathbb{N}^{0} = \varnothing$
is the root. In this case, an individual
![]() $u = u_1u_2\ldots u_k$
is to be interpreted recursively as the
$u = u_1u_2\ldots u_k$
is to be interpreted recursively as the
![]() $u_k$
th child of
$u_k$
th child of
![]() $u_1 \ldots u_{k-1}$
. For example,
$u_1 \ldots u_{k-1}$
. For example,
![]() $1, 2, \ldots$
represent the offspring of
$1, 2, \ldots$
represent the offspring of
![]() $\varnothing$
.
$\varnothing$
.
In Crump–Mode–Jagers (CMJ) branching processes, individuals
![]() $u \in \mathcal{U}$
are equipped with independent copies of a random point process
$u \in \mathcal{U}$
are equipped with independent copies of a random point process
![]() $\xi$
on
$\xi$
on
![]() $\mathbb{R}_+$
. The point process
$\mathbb{R}_+$
. The point process
![]() $\xi$
associates birth times to the offspring of a given individual, and we also may assume that
$\xi$
associates birth times to the offspring of a given individual, and we also may assume that
![]() $\xi$
has some dependence on a random weight W associated with that individual. The process, together with birth times, may be regarded as a random variable in the probability space
$\xi$
has some dependence on a random weight W associated with that individual. The process, together with birth times, may be regarded as a random variable in the probability space
![]() $(\Omega, \Sigma, \mathbb{P}) = \prod_{x \in \mathcal{U}} (\Omega_{x}, \Sigma_{x}, \mathbb{P}_{x})$
, where each
$(\Omega, \Sigma, \mathbb{P}) = \prod_{x \in \mathcal{U}} (\Omega_{x}, \Sigma_{x}, \mathbb{P}_{x})$
, where each
![]() $(\Omega_{x}, \Sigma_{x}, \mathcal{P}_{x})$
is a probability space with
$(\Omega_{x}, \Sigma_{x}, \mathcal{P}_{x})$
is a probability space with
![]() $(\xi_{x}, W_x)$
having the same distribution as
$(\xi_{x}, W_x)$
having the same distribution as
![]() $(\xi,W)$
. We denote by
$(\xi,W)$
. We denote by
![]() $(\sigma_{i}^{x})_{i \in \mathbb{N}}$
points ordered in the point process
$(\sigma_{i}^{x})_{i \in \mathbb{N}}$
points ordered in the point process
![]() $\xi_{x}$
and, for brevity, assume that
$\xi_{x}$
and, for brevity, assume that
![]() $\xi(\{0\}) = 0$
. We also drop the superscript when referring to the point process associated to
$\xi(\{0\}) = 0$
. We also drop the superscript when referring to the point process associated to
![]() $\varnothing$
, so that
$\varnothing$
, so that
![]() $\sigma_{i} \,:\!=\, \sigma^{\varnothing}_i$
. Now, we set
$\sigma_{i} \,:\!=\, \sigma^{\varnothing}_i$
. Now, we set
![]() $\sigma_{\varnothing} \,:\!=\, 0$
and recursively, for
$\sigma_{\varnothing} \,:\!=\, 0$
and recursively, for
![]() $x \in \mathcal{U}$
,
$x \in \mathcal{U}$
,
![]() $\sigma_{xi} \,:\!=\, \sigma_{x} + \sigma^{x}_{i}$
. Finally, we set
$\sigma_{xi} \,:\!=\, \sigma_{x} + \sigma^{x}_{i}$
. Finally, we set
![]() $\mathbb{T}_{t} = \{x \in \mathcal{U}\,:\, \sigma_{x} \leq t\}$
and note that for each
$\mathbb{T}_{t} = \{x \in \mathcal{U}\,:\, \sigma_{x} \leq t\}$
and note that for each
![]() $t \geq 0$
,
$t \geq 0$
,
![]() $\mathbb{T}_{t}$
may be identified with the family tree of the process in the natural way. Informally,
$\mathbb{T}_{t}$
may be identified with the family tree of the process in the natural way. Informally,
![]() $\mathbb{T}_{t}$
can be described as follows: at time zero, there is one vertex
$\mathbb{T}_{t}$
can be described as follows: at time zero, there is one vertex
![]() $\varnothing$
, which reproduces according to
$\varnothing$
, which reproduces according to
![]() $(\xi_{\varnothing}, W_{\varnothing})$
. Thereafter, at times corresponding to points in
$(\xi_{\varnothing}, W_{\varnothing})$
. Thereafter, at times corresponding to points in
![]() $\xi_{\varnothing}$
, descendants of
$\xi_{\varnothing}$
, descendants of
![]() $\varnothing$
are formed, which in turn produce offspring according to the same law. A crucial aspect of the study of CMJ processes is the characteristics
$\varnothing$
are formed, which in turn produce offspring according to the same law. A crucial aspect of the study of CMJ processes is the characteristics
![]() $\phi_{x}$
associated to each element
$\phi_{x}$
associated to each element
![]() $x \in \mathcal{U}$
. For
$x \in \mathcal{U}$
. For
![]() $x \in \mathcal{U}$
, let
$x \in \mathcal{U}$
, let
![]() $\mathcal{U}_{x} \,:\!=\, \left\{xu\,:\, u \in \mathcal{U}\right\}$
. Then the processes
$\mathcal{U}_{x} \,:\!=\, \left\{xu\,:\, u \in \mathcal{U}\right\}$
. Then the processes
![]() $\phi_{x}$
are identically distributed, non-negative stochastic processes on the space
$\phi_{x}$
are identically distributed, non-negative stochastic processes on the space
![]() $(\Omega, \Sigma, \mathbb{P})$
associated with individuals x, which may depend on
$(\Omega, \Sigma, \mathbb{P})$
associated with individuals x, which may depend on
![]() $(\xi_{z}, W_{z})_{z \in \mathcal{U}_{x}}$
. Intuitively, these are processes that track ‘characteristics’ not only of the individual x, but also of its potential offspring
$(\xi_{z}, W_{z})_{z \in \mathcal{U}_{x}}$
. Intuitively, these are processes that track ‘characteristics’ not only of the individual x, but also of its potential offspring
![]() $\{xy\,:\, y \in \mathcal{U}\}$
. We then define the general branching process counted with characteristic as
$\{xy\,:\, y \in \mathcal{U}\}$
. We then define the general branching process counted with characteristic as
thus this function keeps a ‘score’ of characteristics of individuals in the family tree associated with the process up to time t.
Let
![]() $\nu$
be the intensity measure of
$\nu$
be the intensity measure of
![]() $\xi$
, that is,
$\xi$
, that is,
![]() $\nu(B) \,:\!=\, {{\mathbb{E}\!\left[{\xi(B)} \right]}}$
for measurable sets
$\nu(B) \,:\!=\, {{\mathbb{E}\!\left[{\xi(B)} \right]}}$
for measurable sets
![]() $B \subseteq \mathbb{R}_{+}$
. A crucial parameter in the study of CMJ processes is the Malthusian parameter
$B \subseteq \mathbb{R}_{+}$
. A crucial parameter in the study of CMJ processes is the Malthusian parameter
![]() $\alpha$
, which is defined as the solution (if it exists) of
$\alpha$
, which is defined as the solution (if it exists) of
Assume that
![]() $\nu$
is not supported on any lattice, i.e., for any
$\nu$
is not supported on any lattice, i.e., for any
![]() $h > 0$
,
$h > 0$
,
![]() ${{\text{Supp} \!\left( {\nu} \right)}} \subsetneq \{ 0, h, 2h, \ldots\}$
, and that the first moment of
${{\text{Supp} \!\left( {\nu} \right)}} \subsetneq \{ 0, h, 2h, \ldots\}$
, and that the first moment of
![]() $e^{-\alpha u} \nu({\text{d}} u)$
is finite, i.e.,
$e^{-\alpha u} \nu({\text{d}} u)$
is finite, i.e.,
![]() $\int_{0}^{\infty} u e^{-\alpha u} \nu({\text{d}} u) < \infty$
. Nerman [Reference Nerman30] proved the following theorem.
$\int_{0}^{\infty} u e^{-\alpha u} \nu({\text{d}} u) < \infty$
. Nerman [Reference Nerman30] proved the following theorem.
Theorem 2.3. ([Reference Nerman30, Theorem 6.3]) Suppose that there exists
![]() $\lambda < \alpha$
satisfying
$\lambda < \alpha$
satisfying
Then, for any two càdlàg characteristics
![]() $\phi^{(1)}, \phi^{(2)}$
such that
$\phi^{(1)}, \phi^{(2)}$
such that
![]() ${{\mathbb{E}\!\left[{\sup_{t \geq 0} e^{-\lambda t} \phi^{(i)}(t)} \right]}} < \infty, \; i=1, 2,$
we have
${{\mathbb{E}\!\left[{\sup_{t \geq 0} e^{-\lambda t} \phi^{(i)}(t)} \right]}} < \infty, \; i=1, 2,$
we have
almost surely on the event
![]() $\{\left|\mathbb{T}_{t}\right| \rightarrow \infty\}$
.
$\{\left|\mathbb{T}_{t}\right| \rightarrow \infty\}$
.
Recall the definition of
![]() $\rho$
as the point process associated with the jumps in the process Y defined in (9). Then the continuous-time model outlined in Section 2.1 is a CMJ process having
$\rho$
as the point process associated with the jumps in the process Y defined in (9). Then the continuous-time model outlined in Section 2.1 is a CMJ process having
![]() $\rho$
as its associated random point process and weight W. In this case, the Malthusian parameter is given by
$\rho$
as its associated random point process and weight W. In this case, the Malthusian parameter is given by
![]() $\alpha$
in (12), and moreover, Condition C1 implies that the first moment
$\alpha$
in (12), and moreover, Condition C1 implies that the first moment
![]() $\int_{0}^{\infty} t e^{-\alpha t} \hat{\rho}_{\mu}({\text{d}} t)$
is finite.
$\int_{0}^{\infty} t e^{-\alpha t} \hat{\rho}_{\mu}({\text{d}} t)$
is finite.
Theorem 2.1 is now an immediate application of Theorem 2.3.
Proof of Theorem
2.1. Consider the continuous-time branching process outlined in Section 2.1 and denote by
![]() $\sigma^{\prime}_1 < \sigma^{\prime}_2 \cdots$
the times of births of individuals in the process. Then
$\sigma^{\prime}_1 < \sigma^{\prime}_2 \cdots$
the times of births of individuals in the process. Then
![]() ${\mathcal{T}}_n$
has the same distribution as the family tree
${\mathcal{T}}_n$
has the same distribution as the family tree
![]() $\mathbb{T}_{\sigma^{\prime}_n}$
. For any measurable set
$\mathbb{T}_{\sigma^{\prime}_n}$
. For any measurable set
![]() $B \subseteq \mathbb{R}$
, define the characteristics
$B \subseteq \mathbb{R}$
, define the characteristics
![]() $\phi^{(1)}(t) = \mathbf{1}_{\left\{Y(t) = k\ell, W \in B\right\}}$
and
$\phi^{(1)}(t) = \mathbf{1}_{\left\{Y(t) = k\ell, W \in B\right\}}$
and
![]() $\phi^{(2)}(t) = \mathbf{1}_{\{t \geq 0\}}$
, where W denotes the weight of the process Y. Note that
$\phi^{(2)}(t) = \mathbf{1}_{\{t \geq 0\}}$
, where W denotes the weight of the process Y. Note that
![]() $Z^{\phi^{(1)}}(t)$
is the number of individuals with
$Z^{\phi^{(1)}}(t)$
is the number of individuals with
![]() $k\ell$
offspring and weight belonging to B up to time t, while
$k\ell$
offspring and weight belonging to B up to time t, while
![]() $Z^{\phi^{(2)}}(t) = |\mathbb{T}_{t}|$
. Thus,
$Z^{\phi^{(2)}}(t) = |\mathbb{T}_{t}|$
. Thus,
Note that both
![]() $\phi^{(1)}(t)$
and
$\phi^{(1)}(t)$
and
![]() $\phi^{(2)}(t)$
are càdlàg and bounded, and moreover, Condition C1 implies that (16) is satisfied. In addition, the assumption that
$\phi^{(2)}(t)$
are càdlàg and bounded, and moreover, Condition C1 implies that (16) is satisfied. In addition, the assumption that
![]() $f(0,W) > 0$
almost surely implies that
$f(0,W) > 0$
almost surely implies that
![]() $\left|\mathbb{T}_{t}\right| \rightarrow \infty$
almost surely. Thus, by applying Theorem 2.3, we have
$\left|\mathbb{T}_{t}\right| \rightarrow \infty$
almost surely. Thus, by applying Theorem 2.3, we have
 \begin{align} \lim_{t \to \infty} \frac{Z^{\phi^{(1)}}(t)}{Z^{\phi^{(2)}}(t)} &= \alpha \int_0^\infty \text e^{-\alpha s}{{\mathbb{E} \!\left[{\mathbf{1}_{\left\{Y(s) = k\ell, W \in B\right\}}} \right]}} {\text{d}} s \nonumber\\&= {{\mathbb{E}\!\left[{{{\mathbb{E}_{W} \!\left[{ \left(e^{-\alpha \tau_{k}} - e^{-\alpha\tau_{k+1}}\right)} \right]}}\mathbf{1}_{B}(W)} \right]}},\end{align}
\begin{align} \lim_{t \to \infty} \frac{Z^{\phi^{(1)}}(t)}{Z^{\phi^{(2)}}(t)} &= \alpha \int_0^\infty \text e^{-\alpha s}{{\mathbb{E} \!\left[{\mathbf{1}_{\left\{Y(s) = k\ell, W \in B\right\}}} \right]}} {\text{d}} s \nonumber\\&= {{\mathbb{E}\!\left[{{{\mathbb{E}_{W} \!\left[{ \left(e^{-\alpha \tau_{k}} - e^{-\alpha\tau_{k+1}}\right)} \right]}}\mathbf{1}_{B}(W)} \right]}},\end{align}
where the last equality follows from Fubini’s theorem and we recall that
![]() $\tau_{k}$
is the time of the kth event in the process
$\tau_{k}$
is the time of the kth event in the process
![]() $Y_{W}(t)$
. Now, since, when
$Y_{W}(t)$
. Now, since, when
![]() $W = w$
,
$W = w$
,
![]() $\tau_k$
is distributed as a sum of independent exponentially distributed random variables with rates
$\tau_k$
is distributed as a sum of independent exponentially distributed random variables with rates
![]() $f(0,w), f(1,w) \ldots$
, we have
$f(0,w), f(1,w) \ldots$
, we have
 \begin{equation} {{\mathbb{E}\!\left[{{{\mathbb{E}_{W} \!\left[{e^{-\alpha \tau_{k}}} \right]}}\mathbf{1}_{B}(W)} \right]}} = {{\mathbb{E}\!\left[{\left(\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right)\mathbf{1}_{B}(W)} \right]}}.\end{equation}
\begin{equation} {{\mathbb{E}\!\left[{{{\mathbb{E}_{W} \!\left[{e^{-\alpha \tau_{k}}} \right]}}\mathbf{1}_{B}(W)} \right]}} = {{\mathbb{E}\!\left[{\left(\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha} \right)\mathbf{1}_{B}(W)} \right]}}.\end{equation}
Remark 2.4. As noted by the authors of [Reference Rudas, Tóth and Valkó33], Theorem 2.3 can be applied to deduce a number of other properties of the tree; in particular, the analogue of [Reference Rudas, Tóth and Valkó33, Theorem 1] applies in this case as well.
2.3. A strong law for the partition function
We can also apply Theorem 2.3 to show that the Malthusian parameter
![]() $\alpha$
emerges as the almost sure limit of the partition function, under certain conditions on the fitness function f.
$\alpha$
emerges as the almost sure limit of the partition function, under certain conditions on the fitness function f.
Theorem 2.4. Let
![]() $(\mathcal{T}_{t})_{t \geq 0}$
be a
$(\mathcal{T}_{t})_{t \geq 0}$
be a
![]() ${{\left({\mu, f, \ell}\right)}}$
-RIF tree satisfying C1 with Malthusian parameter
${{\left({\mu, f, \ell}\right)}}$
-RIF tree satisfying C1 with Malthusian parameter
![]() $\alpha$
. Moreover, assume that there exists a constant
$\alpha$
. Moreover, assume that there exists a constant
![]() $C < \alpha$
and a non-negative function
$C < \alpha$
and a non-negative function
![]() $\varphi$
with
$\varphi$
with
![]() ${{\mathbb{E} \!\left[{\varphi(W)} \right]}} < \infty$
such that, for all
${{\mathbb{E} \!\left[{\varphi(W)} \right]}} < \infty$
such that, for all
![]() $k \in \mathbb{N}_{0}$
,
$k \in \mathbb{N}_{0}$
,
![]() $f(k,W) \leq C k + \varphi(W)$
almost surely. Then, almost surely,
$f(k,W) \leq C k + \varphi(W)$
almost surely. Then, almost surely,
To apply Theorem 2.3, we need to bound
![]() ${{\mathbb{E}\!\left[{\sup_{t \geq 0} e^{-\lambda t} \phi^{(1)}(t)} \right]}}$
for an appropriate choice of
${{\mathbb{E}\!\left[{\sup_{t \geq 0} e^{-\lambda t} \phi^{(1)}(t)} \right]}}$
for an appropriate choice of
![]() $\lambda < \alpha$
and characteristic
$\lambda < \alpha$
and characteristic
![]() $\phi^{(1)}$
that tracks the evolution of the partition function associated with the process. In order to do so, using the assumptions on f(i, W), we will couple the process Y defined in (9) with an appropriate pure birth process
$\phi^{(1)}$
that tracks the evolution of the partition function associated with the process. In order to do so, using the assumptions on f(i, W), we will couple the process Y defined in (9) with an appropriate pure birth process
![]() $(\mathcal{Y}(t))_{t\geq 0}$
(Lemma 2.3) and apply Doob’s maximal inequality to a martingale associated with
$(\mathcal{Y}(t))_{t\geq 0}$
(Lemma 2.3) and apply Doob’s maximal inequality to a martingale associated with
![]() $(\mathcal{Y}(t))_{t \geq 0}$
(Lemma 2.2). As we will see, our choice of
$(\mathcal{Y}(t))_{t \geq 0}$
(Lemma 2.2). As we will see, our choice of
![]() $\lambda$
will be given by C, and this is the reason for the assumption that
$\lambda$
will be given by C, and this is the reason for the assumption that
![]() $C < \alpha$
in Theorem 2.4.
$C < \alpha$
in Theorem 2.4.
In order to define
![]() $\mathcal{Y}(t)$
, first sample a weight W and set
$\mathcal{Y}(t)$
, first sample a weight W and set
![]() $\mathcal{Y}(0) = 0$
. Then, if
$\mathcal{Y}(0) = 0$
. Then, if
![]() $\mathbb{P}_{w}$
denotes the probability measure associated with the process when the weight is w, define the rates so that
$\mathbb{P}_{w}$
denotes the probability measure associated with the process when the weight is w, define the rates so that
We also let
![]() $\mathcal{Y}_{w}$
denote the process with the same transition rates, but deterministic weight w.
$\mathcal{Y}_{w}$
denote the process with the same transition rates, but deterministic weight w.
It will be beneficial to state a more general result, about pure birth processes
![]() $\left(\mathcal{X}(t)\right)_{t\geq 0}$
with linear rates, from the paper by Holmgren and Janson [Reference Holmgren and Janson20]. For brevity, we adapt the notation and only include some specific statements from both theorems.
$\left(\mathcal{X}(t)\right)_{t\geq 0}$
with linear rates, from the paper by Holmgren and Janson [Reference Holmgren and Janson20]. For brevity, we adapt the notation and only include some specific statements from both theorems.
Lemma 2.1. ([Reference Holmgren and Janson20, Theorem A.6 and Theorem A.7]) Let
![]() $\left(\mathcal{X}(t)\right)_{t\geq 0}$
be a pure birth process with
$\left(\mathcal{X}(t)\right)_{t\geq 0}$
be a pure birth process with
![]() $\mathcal{X}(0) = x_0$
and rates such that
$\mathcal{X}(0) = x_0$
and rates such that
for some constants
![]() $c_1, c_2 > 0$
. Then, for each
$c_1, c_2 > 0$
. Then, for each
![]() $t \geq 0$
,
$t \geq 0$
,
Moreover, if
![]() $x_0 = 0$
, the probability generating function is given by
$x_0 = 0$
, the probability generating function is given by
 \begin{equation} {{\mathbb{E}\!\left[{z^{\mathcal{X}(t)}} \right]}} = \left(\frac{e^{-c_1t}}{1-z\left(1 - e^{-c_1t}\right)}\right)^{c_2/c_1}.\end{equation}
\begin{equation} {{\mathbb{E}\!\left[{z^{\mathcal{X}(t)}} \right]}} = \left(\frac{e^{-c_1t}}{1-z\left(1 - e^{-c_1t}\right)}\right)^{c_2/c_1}.\end{equation}
Finally, we will require Lemma 2.2 and Lemma 2.3.
Lemma 2.2. For any
![]() $w > 0$
, the process
$w > 0$
, the process
![]() $(e^{-C t}\left(\mathcal{Y}_{w}(t) + \varphi(w)/C\right))_{t \geq 0}$
is a martingale with respect to its natural filtration
$(e^{-C t}\left(\mathcal{Y}_{w}(t) + \varphi(w)/C\right))_{t \geq 0}$
is a martingale with respect to its natural filtration
![]() $(\mathcal{F}_t)_{t\geq 0}$
. Moreover,
$(\mathcal{F}_t)_{t\geq 0}$
. Moreover,
 \begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}(t) \right)} \right]}} < \infty.\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}(t) \right)} \right]}} < \infty.\end{equation*}
Proof. The process
![]() $(\mathcal{Y}_{w}(t))_{t \geq 0}$
is a pure birth process satisfying the assumptions of Lemma 2.1, with
$(\mathcal{Y}_{w}(t))_{t \geq 0}$
is a pure birth process satisfying the assumptions of Lemma 2.1, with
![]() $c_1 = C$
and
$c_1 = C$
and
![]() $c_2 = \varphi(w)$
. Therefore, by (19) and the Markov property, for any
$c_2 = \varphi(w)$
. Therefore, by (19) and the Markov property, for any
![]() $t > s >0$
we have
$t > s >0$
we have
which implies the martingale statement.
Moreover, applying (20) for the probability generating function, differentiating twice and evaluating at
![]() $z = 1$
, we obtain
$z = 1$
, we obtain
and thus after some manipulations, we find that for all
![]() $t \geq 0$
$t \geq 0$
Combining this
![]() $L^2$
quadratic bound with Doob’s maximal inequality, we have
$L^2$
quadratic bound with Doob’s maximal inequality, we have
 \begin{align*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}_w(t) \right)} \right]}} & \leq{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\left(\mathcal{Y}_w(t) + \varphi(w)/C\right)\right)} \right]}}\\ & \leq A + B\varphi(w),\end{align*}
\begin{align*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}_w(t) \right)} \right]}} & \leq{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\left(\mathcal{Y}_w(t) + \varphi(w)/C\right)\right)} \right]}}\\ & \leq A + B\varphi(w),\end{align*}
for constants A, B depending only on C. Thus,
 \begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}(t) \right)} \right]}} = {{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}_{W}(t) \right)} \right]}} \leq A + B{{\mathbb{E}\!\left[{\varphi(W)} \right]}} < \infty.\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}(t) \right)} \right]}} = {{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t}\mathcal{Y}_{W}(t) \right)} \right]}} \leq A + B{{\mathbb{E}\!\left[{\varphi(W)} \right]}} < \infty.\end{equation*}
Lemma 2.3. Recall the definition of Y in (9) and assume that there exists a constant
![]() $C < \alpha$
and a non-negative function
$C < \alpha$
and a non-negative function
![]() $\varphi$
with
$\varphi$
with
![]() ${{\mathbb{E}\!\left[{\varphi(W)} \right]}} < \infty$
such that, for all
${{\mathbb{E}\!\left[{\varphi(W)} \right]}} < \infty$
such that, for all
![]() $k \in \mathbb{N}_{0}$
,
$k \in \mathbb{N}_{0}$
,
![]() $f(k,W) \leq C k + \varphi(W)$
almost surely. Then there exists a coupling
$f(k,W) \leq C k + \varphi(W)$
almost surely. Then there exists a coupling
![]() $(\hat{Y}(t),\hat{\mathcal{Y}}(t))_{t \geq 0}$
of
$(\hat{Y}(t),\hat{\mathcal{Y}}(t))_{t \geq 0}$
of
![]() $(Y(t))_{t \geq 0}$
and
$(Y(t))_{t \geq 0}$
and
![]() $(\mathcal{Y}(t))_{t \geq 0}$
such that, for all
$(\mathcal{Y}(t))_{t \geq 0}$
such that, for all
![]() $t \geq 0$
,
$t \geq 0$
,
In the following proof, we denote by
![]() ${\text{Exp}\!\left( {r} \right)}$
the exponential distribution with parameter r.
${\text{Exp}\!\left( {r} \right)}$
the exponential distribution with parameter r.
Proof. First, we sample
![]() $\hat{W}$
from
$\hat{W}$
from
![]() $\mu$
and use this as a common weight for
$\mu$
and use this as a common weight for
![]() $\hat{Y}$
and
$\hat{Y}$
and
![]() $\hat{\mathcal{Y}}$
. Now, let
$\hat{\mathcal{Y}}$
. Now, let
![]() $\left(\varsigma_{i}\right)_{i \geq 0}$
be independent
$\left(\varsigma_{i}\right)_{i \geq 0}$
be independent
![]() ${\text{Exp}\!\left( {f(i, \hat{W})} \right)}$
-distributed random variables. Then, for all
${\text{Exp}\!\left( {f(i, \hat{W})} \right)}$
-distributed random variables. Then, for all
![]() $k > 0$
, set
$k > 0$
, set
![]() $\hat{\tau}_{k} = \sum_{i=0}^{k-1} \varsigma_{i}$
and
$\hat{\tau}_{k} = \sum_{i=0}^{k-1} \varsigma_{i}$
and
The
![]() $\varsigma_{i}$
can be interpreted as the intermittent time between jumps from state i to
$\varsigma_{i}$
can be interpreted as the intermittent time between jumps from state i to
![]() $i+\ell$
. For all
$i+\ell$
. For all
![]() $t> 0$
construct the jump times of
$t> 0$
construct the jump times of
![]() $(\hat{\mathcal{Y}}(t))_{t \geq 0}$
iteratively as follows:
$(\hat{\mathcal{Y}}(t))_{t \geq 0}$
iteratively as follows:
Note that by assumption
 $f(0, \hat{W}) \leq \varphi(\hat{W})$
. Let
$f(0, \hat{W}) \leq \varphi(\hat{W})$
. Let
 $e_{0} \sim {\text{Exp}\!\left( {\varphi(\hat{W}) - f(0,\hat{W})} \right)}$
and set
$e_{0} \sim {\text{Exp}\!\left( {\varphi(\hat{W}) - f(0,\hat{W})} \right)}$
and set
 $\varsigma^{\prime}_{0} = \min\!\left\{e_{0}, \varsigma_{0}\right\}$
. We may interpret
$\varsigma^{\prime}_{0} = \min\!\left\{e_{0}, \varsigma_{0}\right\}$
. We may interpret
 $\varsigma^{\prime}_{0}$
as the time for
$\varsigma^{\prime}_{0}$
as the time for
 $\hat{\mathcal{Y}}$
to jump from 0 to 1.
$\hat{\mathcal{Y}}$
to jump from 0 to 1.Given
 $\varsigma^{\prime}_{0}, \ldots, \varsigma^{\prime}_{j}$
, let
$\varsigma^{\prime}_{0}, \ldots, \varsigma^{\prime}_{j}$
, let
 $q_{j} \,:\!=\, \sum_{i=0}^{j}\varsigma^{\prime}_{i}$
and define
$q_{j} \,:\!=\, \sum_{i=0}^{j}\varsigma^{\prime}_{i}$
and define
 $m_{j} \,:\!=\, \hat{Y}(q_{j})/\ell$
, i.e., the value of
$m_{j} \,:\!=\, \hat{Y}(q_{j})/\ell$
, i.e., the value of
 $\hat{Y}/\ell$
once
$\hat{Y}/\ell$
once
 $\hat{\mathcal{Y}}$
has reached
$\hat{\mathcal{Y}}$
has reached
 $j+1$
. Assume inductively that
$j+1$
. Assume inductively that
 $m_{j} \leq j+1$
and set
$m_{j} \leq j+1$
and set  \begin{equation*}e_{j + 1} \sim {\text{Exp}\!\left( {C(j + 1) +\varphi(\hat{W}) - f\big(m_{j}, \hat{W}\big)} \right)} \quad \text{ and } \quad \varsigma^{\prime}_{j+1} = \min\!\left\{e_{j}, \varsigma_{m_j} \right\}.\end{equation*}
\begin{equation*}e_{j + 1} \sim {\text{Exp}\!\left( {C(j + 1) +\varphi(\hat{W}) - f\big(m_{j}, \hat{W}\big)} \right)} \quad \text{ and } \quad \varsigma^{\prime}_{j+1} = \min\!\left\{e_{j}, \varsigma_{m_j} \right\}.\end{equation*}
Observe that, since
![]() $\varsigma^{\prime}_{j+1} \leq \varsigma_{m_j + 1}$
, we have
$\varsigma^{\prime}_{j+1} \leq \varsigma_{m_j + 1}$
, we have
![]() $m_{j+1} \leq j+2$
, so we may iterate this procedure.
$m_{j+1} \leq j+2$
, so we may iterate this procedure.
It is clear that
![]() $(\hat{Y}(t))_{t \geq 0}$
is distributed like
$(\hat{Y}(t))_{t \geq 0}$
is distributed like
![]() $(Y(t))_{t \geq 0}$
, and using the properties of the exponential distribution one readily confirms that
$(Y(t))_{t \geq 0}$
, and using the properties of the exponential distribution one readily confirms that
![]() $(\hat{\mathcal{Y}}(t))_{t \geq 0}$
is distributed like
$(\hat{\mathcal{Y}}(t))_{t \geq 0}$
is distributed like
![]() $(\mathcal{Y}(t))_{t\geq 0}$
. Finally, the desired inequality follows from the fact that
$(\mathcal{Y}(t))_{t\geq 0}$
. Finally, the desired inequality follows from the fact that
![]() $\hat{\mathcal{Y}}(t)$
always jumps before or at the same time as
$\hat{\mathcal{Y}}(t)$
always jumps before or at the same time as
![]() $\hat{Y}(t)$
.
$\hat{Y}(t)$
.
Proof of Theorem
2.4. Consider the continuous-time embedding of the
![]() ${{\left({\mu, f, \ell}\right)}}$
-RIF tree and define the characteristics
${{\left({\mu, f, \ell}\right)}}$
-RIF tree and define the characteristics
![]() $\phi^{(1)}(t) \,:\!=\, \sum_{k=0}^{\infty} f(k,W) \mathbf{1}_{\{Y(t) = k\ell\}}$
and
$\phi^{(1)}(t) \,:\!=\, \sum_{k=0}^{\infty} f(k,W) \mathbf{1}_{\{Y(t) = k\ell\}}$
and
![]() $\phi^{(2)}(t) \,:\!=\, \mathbf{1}_{\{t \geq 0\}}$
. Recall that we denote by
$\phi^{(2)}(t) \,:\!=\, \mathbf{1}_{\{t \geq 0\}}$
. Recall that we denote by
![]() $(\tau_i)_{i \geq 1}$
the times of the jumps in Y and that, for all
$(\tau_i)_{i \geq 1}$
the times of the jumps in Y and that, for all
![]() $k \geq 0$
,
$k \geq 0$
,
![]() $f(k,W) \leq C k + \varphi(W)$
. Then, by Lemma 2.3, Lemma 2.2, and the assumptions of the theorem,
$f(k,W) \leq C k + \varphi(W)$
. Then, by Lemma 2.3, Lemma 2.2, and the assumptions of the theorem,
 \begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t} \phi^{(1)}(t)\right)} \right]}} \stackrel{\text{Lem.}\ 2.3}{\leq} {{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t} \left(C \mathcal{Y}_{W}(t) + \varphi(W)\right) \right)} \right]}} \stackrel{\text{Lem.}\ 2.2}{<} \infty.\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t} \phi^{(1)}(t)\right)} \right]}} \stackrel{\text{Lem.}\ 2.3}{\leq} {{\mathbb{E}\!\left[{\sup_{t \geq 0} \left(e^{-C t} \left(C \mathcal{Y}_{W}(t) + \varphi(W)\right) \right)} \right]}} \stackrel{\text{Lem.}\ 2.2}{<} \infty.\end{equation*}
Now, in this case
![]() $Z^{\phi^{(1)}}(t)$
is the total sum of fitnesses of individuals born up to time t, while
$Z^{\phi^{(1)}}(t)$
is the total sum of fitnesses of individuals born up to time t, while
![]() $Z^{\phi^{(2)}}(t) = |\mathcal{T}_{t}|$
. Thus, by Theorem 2.3 and Fubini’s theorem in the second equality, almost surely we have
$Z^{\phi^{(2)}}(t) = |\mathcal{T}_{t}|$
. Thus, by Theorem 2.3 and Fubini’s theorem in the second equality, almost surely we have
 \begin{align} \lim_{n \to \infty} \frac{\mathcal{Z}_{n}}{\ell n} & = \alpha \int_{0}^{\infty} e^{- \alpha s} {{\mathbb{E}\!\left[{\sum_{k=0}^{\infty} f(k,W) \mathbf{1}_{\{Y(s) = k\ell\}}}\right]}} {\text{d}} s ={{\mathbb{E}\!\left[{\sum_{k=0}^{\infty} f(k,W) \left(e^{-\alpha \tau_{k}} - e^{-\alpha \tau_{k+1}}\right)} \right]}} \end{align}
\begin{align} \lim_{n \to \infty} \frac{\mathcal{Z}_{n}}{\ell n} & = \alpha \int_{0}^{\infty} e^{- \alpha s} {{\mathbb{E}\!\left[{\sum_{k=0}^{\infty} f(k,W) \mathbf{1}_{\{Y(s) = k\ell\}}}\right]}} {\text{d}} s ={{\mathbb{E}\!\left[{\sum_{k=0}^{\infty} f(k,W) \left(e^{-\alpha \tau_{k}} - e^{-\alpha \tau_{k+1}}\right)} \right]}} \end{align}
 \begin{align} \nonumber & = {{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \frac{\alpha f(k,W)}{f(k,W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}}.\end{align}
\begin{align} \nonumber & = {{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \frac{\alpha f(k,W)}{f(k,W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}}.\end{align}
Now, recall that by (12) we have
 \begin{equation*}{{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \frac{f(k,W)}{f(k,W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}} = \frac{1}{\ell},\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\sum_{k=1}^{\infty} \frac{f(k,W)}{f(k,W) + \alpha}\prod_{i=0}^{k-1} \frac{f(i,W)}{f(i,W) + \alpha}} \right]}} = \frac{1}{\ell},\end{equation*}
and combining this with (21) proves the result.
2.4. Examples of applications of Theorem 2.1
2.4.1. Weighted Cayley trees
Consider the model where
![]() $f(k,W) = 0$
for
$f(k,W) = 0$
for
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $f(0,W) = g(W)$
. Thus, at each step, a vertex with degree 0 is chosen and produces
$f(0,W) = g(W)$
. Thus, at each step, a vertex with degree 0 is chosen and produces
![]() $\ell$
children, and thus this model produces an
$\ell$
children, and thus this model produces an
![]() $(\ell + 1)$
-Cayley tree, i.e., a tree in which each node that is not a leaf has degree
$(\ell + 1)$
-Cayley tree, i.e., a tree in which each node that is not a leaf has degree
![]() $\ell + 1$
. Without loss of generality, by considering the pushforward of
$\ell + 1$
. Without loss of generality, by considering the pushforward of
![]() $\mu$
under g if necessary, we may assume that
$\mu$
under g if necessary, we may assume that
![]() $g(W) = W$
. In this case,
$g(W) = W$
. In this case,
![]() $\hat{\rho}_{\mu}(\lambda) = \ell \cdot {{\mathbb{E}\!\left[{\frac{W}{W + \lambda}} \right]}}$
and thus C1 is satisfied as long as
$\hat{\rho}_{\mu}(\lambda) = \ell \cdot {{\mathbb{E}\!\left[{\frac{W}{W + \lambda}} \right]}}$
and thus C1 is satisfied as long as
![]() $\ell \geq 2$
. Thus,
$\ell \geq 2$
. Thus,
![]() $p^{\alpha}_{k}(B) = 0$
for all
$p^{\alpha}_{k}(B) = 0$
for all
![]() $k \geq 2$
, and
$k \geq 2$
, and
This rigorously confirms a result of Bianconi [Reference Bianconi4]. Note, however, that in [Reference Bianconi4]
![]() $\alpha$
is described as the almost sure limit of the partition function, and we may only apply Theorem 2.4 under the assumption that
$\alpha$
is described as the almost sure limit of the partition function, and we may only apply Theorem 2.4 under the assumption that
![]() ${{\mathbb{E} \!\left[W \right]}}< \infty$
.
${{\mathbb{E} \!\left[W \right]}}< \infty$
.
In the notation of [Reference Bianconi4], the weights W are called ‘energies’, using the symbol
![]() $\epsilon$
, the function
$\epsilon$
, the function
![]() $g(\epsilon) \,:\!=\, e^{\beta \epsilon}$
, where
$g(\epsilon) \,:\!=\, e^{\beta \epsilon}$
, where
![]() $\beta > 0$
is a parameter of the model, and
$\beta > 0$
is a parameter of the model, and
![]() $\alpha \,:\!=\, e^{\beta \mu_{F}}$
is described as the limit of the partition function. Thus, the proportion of vertices with out-degree 0 with ‘energy’ belonging to some measurable set B is
$\alpha \,:\!=\, e^{\beta \mu_{F}}$
is described as the limit of the partition function. Thus, the proportion of vertices with out-degree 0 with ‘energy’ belonging to some measurable set B is
which is known as a Fermi–Dirac distribution in physics.
2.4.2. Weighted random recursive trees
In the case that
![]() $f(k,W) = W$
, we obtain a model of weighted random recursive trees with independent weights and C1 is satisfied with
$f(k,W) = W$
, we obtain a model of weighted random recursive trees with independent weights and C1 is satisfied with
![]() $\alpha = {{\mathbb{E}\!\left[{W} \right]}}$
provided
$\alpha = {{\mathbb{E}\!\left[{W} \right]}}$
provided
![]() ${{\mathbb{E}\!\left[{W} \right]}} < \infty$
. Theorem 2.1 then implies that
${{\mathbb{E}\!\left[{W} \right]}} < \infty$
. Theorem 2.1 then implies that
almost surely. This was observed in the case
![]() $\ell = 1$
by the authors of [Reference Fountoulakis, Iyer, Mailler and Sulzbach17, Proposition 3]. Note also that in this case Theorem 2.4 coincides with the usual strong law of large numbers.
$\ell = 1$
by the authors of [Reference Fountoulakis, Iyer, Mailler and Sulzbach17, Proposition 3]. Note also that in this case Theorem 2.4 coincides with the usual strong law of large numbers.
The weighted random recursive tree has a natural generalisation to affine fitness functions. This is the topic of the next section.
3. Generalised preferential attachment trees with fitnesses
In this section, we study
![]() $\left({\mu, f, \ell}\right)$
-RIF trees in the specific case when the function f takes an affine form, that is,
$\left({\mu, f, \ell}\right)$
-RIF trees in the specific case when the function f takes an affine form, that is,
![]() $f(i,W) = ig(W) + h(W)$
, for positive, measurable functions g, h. We call this particular case of the model a generalised preferential attachment tree with fitness (which we abbreviate as a GPAF-tree). The affine form of this model means that it is tractable to apply the coupling methods outlined in Section 3.2.3, when Condition C1 fails. Moreover, this model is general enough to be an extension not only of the weighted random recursive tree, but also of the additive and multiplicative models studied in [Reference Bhamidi3, Reference Borgs, Chayes, Daskalakis and Roch8].
$f(i,W) = ig(W) + h(W)$
, for positive, measurable functions g, h. We call this particular case of the model a generalised preferential attachment tree with fitness (which we abbreviate as a GPAF-tree). The affine form of this model means that it is tractable to apply the coupling methods outlined in Section 3.2.3, when Condition C1 fails. Moreover, this model is general enough to be an extension not only of the weighted random recursive tree, but also of the additive and multiplicative models studied in [Reference Bhamidi3, Reference Borgs, Chayes, Daskalakis and Roch8].
Below, in Section 3.1, we apply the theory of the previous section to this model when C1 is satisfied. In satisfied. In Section 3.2, we analyse the model when Condition C1 fails by having
![]() $m(\lambda, \mathbb{R}_{+}) \leq 1$
for all
$m(\lambda, \mathbb{R}_{+}) \leq 1$
for all
![]() $\lambda > 0$
such that
$\lambda > 0$
such that
![]() $m(\lambda, \mathbb{R}_{+}) < \infty$
, stating and proving Theorem 3.1. Then, in Section 3.3, we analyse the model when Condition C1 fails by having
$m(\lambda, \mathbb{R}_{+}) < \infty$
, stating and proving Theorem 3.1. Then, in Section 3.3, we analyse the model when Condition C1 fails by having
![]() $m(\lambda, \mathbb{R}_{+}) = \infty$
for all
$m(\lambda, \mathbb{R}_{+}) = \infty$
for all
![]() $\lambda > 0$
, stating and proving Theorem 3.2.
$\lambda > 0$
, stating and proving Theorem 3.2.
Note that in this section, we formulate our results in terms of functions g and h of a random variable W taking values in
![]() $\mathbb{R}_{+}$
. However, in the vein of Remark 2.3, we expect these results to extend to cases where g and h may depend on more general random variables. For example, there is no loss of generality in assuming g and h depend on possibly correlated random variables
$\mathbb{R}_{+}$
. However, in the vein of Remark 2.3, we expect these results to extend to cases where g and h may depend on more general random variables. For example, there is no loss of generality in assuming g and h depend on possibly correlated random variables
![]() $W_1$
and
$W_1$
and
![]() $W_2$
assigned to a given vertex. In this case, the coupling technique applied in Section 3.2.3 needs to be adjusted accordingly, with appropriate ‘truncations’ of the vector
$W_2$
assigned to a given vertex. In this case, the coupling technique applied in Section 3.2.3 needs to be adjusted accordingly, with appropriate ‘truncations’ of the vector
![]() $(W_1,W_2)$
.
$(W_1,W_2)$
.
3.1. When the GPAF-tree satisfies Condition C1
In the context of the GPAF-tree, Condition C1 states that there exists
![]() $\lambda > 0$
such that
$\lambda > 0$
such that
 \begin{equation*}m(\lambda, \mathbb{R}_{+}) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{g(W)i +h(W)}{g(W)i + h(W) + \lambda}} \right]}} > 1.\end{equation*}
\begin{equation*}m(\lambda, \mathbb{R}_{+}) = \ell \cdot {{\mathbb{E}\!\left[{\sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{g(W)i +h(W)}{g(W)i + h(W) + \lambda}} \right]}} > 1.\end{equation*}
First recall the definition of the birth process Y from (9) in Section 2, with
![]() $f(k,{W}) = g(W)k + h(W)$
. By applying (19) from Lemma 2.1 and the initial condition
$f(k,{W}) = g(W)k + h(W)$
. By applying (19) from Lemma 2.1 and the initial condition
![]() $Y(0) = 0$
, for any
$Y(0) = 0$
, for any
![]() $w \in \mathbb{R}_{+}$
we have
$w \in \mathbb{R}_{+}$
we have
Now, (10) and (11) in Section 2 showed that
 \begin{equation} \ell \cdot \sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{g(W)i +h(W)}{g(W)i + h(W) + \lambda} = \int_{0}^{\infty} \lambda e^{-\lambda s} {{\mathbb{E}_{w} \!\left[{Y(s)} \right]}} {\text{d}} s =\begin{cases}\frac{h(w)}{\lambda/\ell - g(w)} & \text{if } \lambda/ \ell > g(w); \\[5pt]\infty & \text{otherwise}.\end{cases}\end{equation}
\begin{equation} \ell \cdot \sum_{n=1}^{\infty} \prod_{i=0}^{n-1} \frac{g(W)i +h(W)}{g(W)i + h(W) + \lambda} = \int_{0}^{\infty} \lambda e^{-\lambda s} {{\mathbb{E}_{w} \!\left[{Y(s)} \right]}} {\text{d}} s =\begin{cases}\frac{h(w)}{\lambda/\ell - g(w)} & \text{if } \lambda/ \ell > g(w); \\[5pt]\infty & \text{otherwise}.\end{cases}\end{equation}
For a measurable function
![]() $g\,:\,\mathbb{R}_{+} \rightarrow \mathbb{R}_{+}$
we define
$g\,:\,\mathbb{R}_{+} \rightarrow \mathbb{R}_{+}$
we define
![]() $\text{ess sup}{(g)}$
by
$\text{ess sup}{(g)}$
by
Therefore by (22), for
![]() $\lambda \geq \ell \cdot \text{ess sup}{(g)}$
we have
$\lambda \geq \ell \cdot \text{ess sup}{(g)}$
we have
while if
![]() $\lambda < \ell \cdot \text{ess sup}{(g)}$
we have
$\lambda < \ell \cdot \text{ess sup}{(g)}$
we have
![]() $m(\lambda, \mathbb{R}_{+}) = \infty$
. Thus, Condition C1 is satisfied if
$m(\lambda, \mathbb{R}_{+}) = \infty$
. Thus, Condition C1 is satisfied if
![]() $\text{ess sup}{(g)} < \infty$
,
$\text{ess sup}{(g)} < \infty$
,
![]() ${{\mathbb{E} \!\left[{h(W)} \right]}} < \infty$
, and for some
${{\mathbb{E} \!\left[{h(W)} \right]}} < \infty$
, and for some
![]() $\lambda \geq \ell \cdot \text{ess sup}{(g)}$
$\lambda \geq \ell \cdot \text{ess sup}{(g)}$
As a result, the Malthusian parameter
![]() $\alpha$
appearing in Condition C1 is given by the unique
$\alpha$
appearing in Condition C1 is given by the unique
![]() $\alpha > 0$
such that
$\alpha > 0$
such that
Note that the parameter
![]() $\ell$
in the model has the effect of re-scaling the Malthusian parameter
$\ell$
in the model has the effect of re-scaling the Malthusian parameter
![]() $\alpha$
. Also, since
$\alpha$
. Also, since
![]() $\alpha \geq \ell \cdot \text{ess sup}(g)$
, if
$\alpha \geq \ell \cdot \text{ess sup}(g)$
, if
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, Theorem 2.4 applies and
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, Theorem 2.4 applies and
![]() $\alpha$
may also be interpreted as the almost sure limit of the partition function associated with the process. Now, in the context of this model, the limiting value
$\alpha$
may also be interpreted as the almost sure limit of the partition function associated with the process. Now, in the context of this model, the limiting value
![]() $p^{\alpha}_{k}({\cdot})$
from Theorem 2.1 is such that
$p^{\alpha}_{k}({\cdot})$
from Theorem 2.1 is such that
 \begin{equation} p^{\alpha}_{k}(B) = {{\mathbb{E}\!\left[{\frac{\alpha}{g(W)k + h(W) + \alpha} \prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \alpha} \mathbf{1}_{B}(W)} \right]}}.\end{equation}
\begin{equation} p^{\alpha}_{k}(B) = {{\mathbb{E}\!\left[{\frac{\alpha}{g(W)k + h(W) + \alpha} \prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \alpha} \mathbf{1}_{B}(W)} \right]}}.\end{equation}
Now, recall Stirling’s approximation, which states that
as
![]() $z \to \infty$
. If
$z \to \infty$
. If
![]() $g(W) > 0$
on B, by dividing the numerator and denominator of terms inside the product in (24), we obtain a ratio of gamma functions. Thus, by applying Stirling’s approximation, on any measurable set B on which g, h are bounded, we have
$g(W) > 0$
on B, by dividing the numerator and denominator of terms inside the product in (24), we obtain a ratio of gamma functions. Thus, by applying Stirling’s approximation, on any measurable set B on which g, h are bounded, we have
where
![]() $c_{B}$
, which comes from the term outside the product in (24), depends on g and h but not k. Thus, the distribution of
$c_{B}$
, which comes from the term outside the product in (24), depends on g and h but not k. Thus, the distribution of
![]() $(p^{\alpha}_{k}(B))_{k \in \mathbb{N}_{0}}$
follows what one might describe as an ‘averaged’ power law. Moreover, in the case that
$(p^{\alpha}_{k}(B))_{k \in \mathbb{N}_{0}}$
follows what one might describe as an ‘averaged’ power law. Moreover, in the case that
![]() $\ell = 1$
, we have
$\ell = 1$
, we have
![]() $\alpha \geq \text{ess sup}(g)$
; thus,
$\alpha \geq \text{ess sup}(g)$
; thus,
for some
![]() $c^{\prime} > 0$
. It has been observed that real-world complex networks have power law degree distributions where the observed power law exponent lies between 2 and 3 (see, for example, [Reference Van der Hofstad37]). Note that by (23),
$c^{\prime} > 0$
. It has been observed that real-world complex networks have power law degree distributions where the observed power law exponent lies between 2 and 3 (see, for example, [Reference Van der Hofstad37]). Note that by (23),
![]() $\alpha$
depends on both h and g, so that keeping g fixed and making h smaller has the effect of reducing the exponent of the power law.
$\alpha$
depends on both h and g, so that keeping g fixed and making h smaller has the effect of reducing the exponent of the power law.
In the remainder of this section we set
![]() $\ell =1$
, for brevity. The arguments may be adapted in a similar manner to the case
$\ell =1$
, for brevity. The arguments may be adapted in a similar manner to the case
![]() $\ell >1$
.
$\ell >1$
.
3.2. A condensation phenomenon in the GPAF-tree when Condition C1 fails Condition C1 fails
Recall that, in the GPAF-tree, if
![]() $\lambda \geq \text{ess sup}{(g)}$
we have
$\lambda \geq \text{ess sup}{(g)}$
we have
and if
![]() $\lambda < \text{ess sup}{(g)}$
we have
$\lambda < \text{ess sup}{(g)}$
we have
![]() $m(\lambda, \mathbb{R}_{+}) = \infty$
. If we define
$m(\lambda, \mathbb{R}_{+}) = \infty$
. If we define
in this subsection, we consider the case that the GPAF-tree fails to satisfy Condition C1 by having
![]() $m(\lambda, \mathbb{R}_{+}) \leq 1$
for all
$m(\lambda, \mathbb{R}_{+}) \leq 1$
for all
![]() $\lambda \in \Lambda$
. We show that in this case the GPAF-tree satisfies a formula for the degree distribution of the same form as (3). Moreover, if
$\lambda \in \Lambda$
. We show that in this case the GPAF-tree satisfies a formula for the degree distribution of the same form as (3). Moreover, if
![]() $\lambda^*\,:\!=\, \inf{\left(\Lambda\right)}$
and
$\lambda^*\,:\!=\, \inf{\left(\Lambda\right)}$
and
![]() $m(\lambda^*, \mathbb{R}_{+}) < 1$
, this model exhibits a condensation phenomenon, as described in Theorem 3.1. We remark that such results have been proved for the case of the preferential attachment tree with multiplicative fitness, i.e., the case
$m(\lambda^*, \mathbb{R}_{+}) < 1$
, this model exhibits a condensation phenomenon, as described in Theorem 3.1. We remark that such results have been proved for the case of the preferential attachment tree with multiplicative fitness, i.e., the case
![]() $h \equiv g$
, in [Reference Dereich and Ortgiese14], in a more general framework; that is to say, encompassing other models apart from a tree.
$h \equiv g$
, in [Reference Dereich and Ortgiese14], in a more general framework; that is to say, encompassing other models apart from a tree.
In Section 3.2.1 we state our main result, Theorem 3.1; we discuss interesting implications in Section 3.2.2. In Section 3.2.3 we state and prove Lemma 3.1, which is the crucial tool used in proofs of the theorem. The proof of Theorem 3.1 is deferred to Section 3.2.4.
Remark 3.1. If
![]() ${\mathcal{T}}$
does not satisfy
${\mathcal{T}}$
does not satisfy
![]() ${\textbf{C1}}$
and
${\textbf{C1}}$
and
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, we must have
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, we must have
![]() $\mu\!\left(\left\{x\,:\, g(x) = \text{ess sup }{g}\right\}\right) = 0$
, since otherwise, for each
$\mu\!\left(\left\{x\,:\, g(x) = \text{ess sup }{g}\right\}\right) = 0$
, since otherwise, for each
![]() $\lambda > \lambda^{*}$
, we have
$\lambda > \lambda^{*}$
, we have
![]() $m(\lambda, \mathbb{R}_+) < \infty$
, and by monotone convergence
$m(\lambda, \mathbb{R}_+) < \infty$
, and by monotone convergence
![]() $\lim_{\lambda \downarrow \lambda^*} m(\lambda, \mathbb{R}_+) \uparrow \infty$
.
$\lim_{\lambda \downarrow \lambda^*} m(\lambda, \mathbb{R}_+) \uparrow \infty$
.
3.2.1. Theorem 3.1: condensation in the GPAF-tree
Our main result in this subsection is the following theorem, which demonstrates the possibility of condensation in this model. Recall that in this section, we have
![]() $\lambda^* = \text{ess sup}{(g)}$
. We then define the following family of sets of positive
$\lambda^* = \text{ess sup}{(g)}$
. We then define the following family of sets of positive
![]() $\mu$
-measure, depending on a parameter
$\mu$
-measure, depending on a parameter
![]() $\varepsilon > 0$
:
$\varepsilon > 0$
:
Theorem 3.1. Suppose
![]() ${\mathcal{T}} = \left(\mathcal{T}_{t}\right)_{t \geq 0}$
is a GPAF-tree, with associated functions g, where g is bounded,
${\mathcal{T}} = \left(\mathcal{T}_{t}\right)_{t \geq 0}$
is a GPAF-tree, with associated functions g, where g is bounded,
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, and Condition C1 fails. Then we have the following assertions:
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, and Condition C1 fails. Then we have the following assertions:
-
1. For any measurable set B such that for some
 $\varepsilon > 0$
we have
$\varepsilon > 0$
we have
 $B \subseteq \mathcal{M}^{c}_{\varepsilon}$
, In particular, if
$B \subseteq \mathcal{M}^{c}_{\varepsilon}$
, In particular, if \begin{equation*} \frac{\Xi(t,B)}{\ell t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{B}(W)} \right]}}, \quad {almost\ surely.}\end{equation*}
for
\begin{equation*} \frac{\Xi(t,B)}{\ell t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{B}(W)} \right]}}, \quad {almost\ surely.}\end{equation*}
for \begin{equation*}{{\mathbb{E}\!\left[{\frac{h(W)}{g({w^{*}}) - g(W)}} \right]}} < 1,\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\frac{h(W)}{g({w^{*}}) - g(W)}} \right]}} < 1,\end{equation*}
 $\varepsilon > 0$
sufficiently small we have so that this model exhibits a condensation phenomenon, as described before Conjecture 1.1 in Section 1.3.
$\varepsilon > 0$
sufficiently small we have so that this model exhibits a condensation phenomenon, as described before Conjecture 1.1 in Section 1.3. \begin{equation*}\frac{\Xi(t,\mathcal{M}_{\varepsilon})}{\ell t} \xrightarrow{t \to \infty} 1 - {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{\mathcal{M}^{c}_{\varepsilon}}(W)} \right]}} > {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{\mathcal{M}_{\varepsilon}}(W)} \right]}} = m(\lambda^*, \mathcal{M}_{\varepsilon}),\end{equation*}
\begin{equation*}\frac{\Xi(t,\mathcal{M}_{\varepsilon})}{\ell t} \xrightarrow{t \to \infty} 1 - {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{\mathcal{M}^{c}_{\varepsilon}}(W)} \right]}} > {{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^{*} - g(W)} \mathbf{1}_{\mathcal{M}_{\varepsilon}}(W)} \right]}} = m(\lambda^*, \mathcal{M}_{\varepsilon}),\end{equation*}
-
2. For any measurable set
 $B \subseteq \mathbb{R}_{+}$
, almost surely we have
$B \subseteq \mathbb{R}_{+}$
, almost surely we have  \begin{equation*} \frac{N_{k}(t,B)}{t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{\lambda^{*}}{g(W)k + h(W) + \lambda^{*}} \prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \lambda^{*}} \mathbf{1}_{B}(W)} \right]}} = p^{\lambda^{*}}_{k}(B).\end{equation*}
\begin{equation*} \frac{N_{k}(t,B)}{t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{\lambda^{*}}{g(W)k + h(W) + \lambda^{*}} \prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \lambda^{*}} \mathbf{1}_{B}(W)} \right]}} = p^{\lambda^{*}}_{k}(B).\end{equation*}
-
3. The partition function satisfies
 \begin{equation*}\frac{{\mathcal{Z}}_{t}}{t} \xrightarrow{t \to \infty} \lambda^{*}, \quad \text{almost surely.} \end{equation*}
\begin{equation*}\frac{{\mathcal{Z}}_{t}}{t} \xrightarrow{t \to \infty} \lambda^{*}, \quad \text{almost surely.} \end{equation*}
Suppose that
![]() ${w^{*}} \,:\!=\, \sup{\left({{\text{Supp} \!\left( {\mu} \right)}}\right)} < \infty$
,
${w^{*}} \,:\!=\, \sup{\left({{\text{Supp} \!\left( {\mu} \right)}}\right)} < \infty$
,
![]() ${{\text{Supp} \!\left( {\mu} \right)}} \subseteq [0,{w^{*}}]$
, and g is increasing. Define the measure
${{\text{Supp} \!\left( {\mu} \right)}} \subseteq [0,{w^{*}}]$
, and g is increasing. Define the measure
![]() $\pi({\cdot})$
so that, for any measurable set B,
$\pi({\cdot})$
so that, for any measurable set B,
Then Assertion 1 of Theorem 3.1 leads to the following result.
Corollary 3.1. Under the above assumptions, with respect to the weak topology,
Remark 3.2. Corollary 3.1 is the form in which condensation results usually appear in the literature, showing that the limit of the sequence
![]() $\frac{\Xi(t,\cdot)}{\ell t}$
is no longer absolutely continuous with respect to
$\frac{\Xi(t,\cdot)}{\ell t}$
is no longer absolutely continuous with respect to
![]() $\mu$
. In this regard, Corollary 3.1 generalises the case
$\mu$
. In this regard, Corollary 3.1 generalises the case
![]() $f(i,W) = (i+1)W$
which has already been proved in [Reference Borgs, Chayes, Daskalakis and Roch8].
$f(i,W) = (i+1)W$
which has already been proved in [Reference Borgs, Chayes, Daskalakis and Roch8].
Proof of Corollary
3.1. In view of the portmanteau theorem, it suffices to prove that, almost surely, for any open set O of
![]() $[0, {w^{*}}]$
we have
$[0, {w^{*}}]$
we have
Now, it is well known that there exists a countable family of measurable sets
![]() $D_{1}, D_2, \ldots$
such that any open subset of
$D_{1}, D_2, \ldots$
such that any open subset of
![]() $[0, {w^{*}}]$
may be expressed as a countable disjoint union of elements of this family. For example, one may take the set of all dyadic intervals, with endpoints of the form
$[0, {w^{*}}]$
may be expressed as a countable disjoint union of elements of this family. For example, one may take the set of all dyadic intervals, with endpoints of the form
![]() $j \cdot 2^{-n} {w^{*}}$
,
$j \cdot 2^{-n} {w^{*}}$
,
![]() $(j+1) \cdot 2^{-n} {w^{*}}$
, where
$(j+1) \cdot 2^{-n} {w^{*}}$
, where
![]() $j, n \in \mathbb{N}_{0}$
. Fix such a family. Now, by Assertion 1 of Theorem 3.1, it is the case that, almost surely,
$j, n \in \mathbb{N}_{0}$
. Fix such a family. Now, by Assertion 1 of Theorem 3.1, it is the case that, almost surely,
where
![]() $\mathcal{C}$
is the countable collection of sets
$\mathcal{C}$
is the countable collection of sets
Now, let O be an arbitrary open set. First, suppose that
![]() ${w^{*}} \notin O$
. Then, for a pairwise disjoint collection
${w^{*}} \notin O$
. Then, for a pairwise disjoint collection
![]() $D_{i_1}, D_{i_2}, \ldots$
such that
$D_{i_1}, D_{i_2}, \ldots$
such that
![]() $O = \bigcup_{\ell \in \mathbb{N}} D_{i_\ell}$
, for each
$O = \bigcup_{\ell \in \mathbb{N}} D_{i_\ell}$
, for each
![]() $j, k \in \mathbb{N}$
we have
$j, k \in \mathbb{N}$
we have
 \begin{equation*}\liminf_{t \to \infty} \frac{\Xi(t,O)}{t} \geq \sum_{\ell = 1}^{k} \liminf_{t \to \infty} \frac{\Xi\big(t, D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big)}{t} \geq \sum_{\ell = 1}^{k} \pi\big(D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big).\end{equation*}
\begin{equation*}\liminf_{t \to \infty} \frac{\Xi(t,O)}{t} \geq \sum_{\ell = 1}^{k} \liminf_{t \to \infty} \frac{\Xi\big(t, D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big)}{t} \geq \sum_{\ell = 1}^{k} \pi\big(D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big).\end{equation*}
Taking limits in j and k, the right-hand side converges to
![]() $\pi(O)$
, as required. On the other hand, if
$\pi(O)$
, as required. On the other hand, if
![]() ${w^{*}} \in O$
, since g is increasing, for each
${w^{*}} \in O$
, since g is increasing, for each
![]() $\varepsilon > 0$
there exists
$\varepsilon > 0$
there exists
![]() $\delta = \delta(\varepsilon) > 0$
such that
$\delta = \delta(\varepsilon) > 0$
such that
![]() $\mathcal{M}_{\varepsilon} \subseteq [{w^{*}} - \delta, {w^{*}}]$
. Therefore, because O is open, for all j sufficiently large, we have
$\mathcal{M}_{\varepsilon} \subseteq [{w^{*}} - \delta, {w^{*}}]$
. Therefore, because O is open, for all j sufficiently large, we have
![]() $\mathcal{M}_{1/j} \subseteq O$
. But then, for a pairwise disjoint collection
$\mathcal{M}_{1/j} \subseteq O$
. But then, for a pairwise disjoint collection
![]() $D_{i_1}, D_{i_2}, \ldots$
such that
$D_{i_1}, D_{i_2}, \ldots$
such that
![]() $O = \bigcup_{\ell \in \mathbb{N}} D_{i_\ell}$
, we have
$O = \bigcup_{\ell \in \mathbb{N}} D_{i_\ell}$
, we have
 \begin{equation*}O = \mathcal{M}_{1/j} \cup \left(\bigcup_{\ell \in \mathbb{N}} D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\right).\end{equation*}
\begin{equation*}O = \mathcal{M}_{1/j} \cup \left(\bigcup_{\ell \in \mathbb{N}} D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\right).\end{equation*}
Therefore,
 \begin{align*}\liminf_{t \to \infty} \frac{\Xi(t,O)}{t} &\geq \liminf_{t \to \infty} \frac{\Xi(t, \mathcal{M}_{1/j})}{t} + \sum_{\ell = 1}^{k} \liminf_{t \to \infty} \frac{\Xi\big(t, D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big)}{t}\\ & \geq \pi(\mathcal{M}_{1/j}) + \sum_{\ell = 1}^{k} \pi\big(D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big),\end{align*}
\begin{align*}\liminf_{t \to \infty} \frac{\Xi(t,O)}{t} &\geq \liminf_{t \to \infty} \frac{\Xi(t, \mathcal{M}_{1/j})}{t} + \sum_{\ell = 1}^{k} \liminf_{t \to \infty} \frac{\Xi\big(t, D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big)}{t}\\ & \geq \pi(\mathcal{M}_{1/j}) + \sum_{\ell = 1}^{k} \pi\big(D_{i_\ell} \cap \mathcal{M}^{c}_{1/j}\big),\end{align*}
so that, by again taking limits in j and k, the right-hand side converges to
![]() $\pi(O)$
. The result follows.
$\pi(O)$
. The result follows.
3.2.2. Some interesting implications of the condensation phenomenon
The condensation result in Theorem 3.1 has interesting implications for the GPAF-tree. Informally, the parameter g(w) measures the extent to which the ‘popularity’ of a vertex with weight w is reinforced by the number of its neighbours, while the parameter h(w) represents its ‘initial popularity’. The condensation phenomenon then depends on both
![]() $\mu$
and h, in the sense that condensation occurs if vertices of high weight are ‘rare enough’ and the initial popularity is ‘low enough’. More precisely, if
$\mu$
and h, in the sense that condensation occurs if vertices of high weight are ‘rare enough’ and the initial popularity is ‘low enough’. More precisely, if
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
and
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
and
![]() $\lambda^{*} < \infty$
we see that the tree displays the following interesting features:
$\lambda^{*} < \infty$
we see that the tree displays the following interesting features:
-
1. By Remark 3.1, if
 $\mu$
and g are such that
$\mu$
and g are such that
 ${{\mathbb{E}\!\left[{\frac{1}{\lambda^* - g(W)}} \right]}} = \infty$
, Condition C1 is satisfied in this model, and thus, the model does not demonstrate a condensation phenomenon.
${{\mathbb{E}\!\left[{\frac{1}{\lambda^* - g(W)}} \right]}} = \infty$
, Condition C1 is satisfied in this model, and thus, the model does not demonstrate a condensation phenomenon. -
2. Otherwise, if
 $\mu$
and g are such that
$\mu$
and g are such that
 ${{\mathbb{E}\!\left[{\frac{1}{\lambda^* - g(W)}} \right]}} = {C^{\prime}} < \infty$
, then either Condition C1 is satisfied in the first case but fails in the second case. However, in the second case, if the inequality is strict, condensation arises. Therefore, for fixed g, condensation in this model arises if we reduce h sufficiently pointwise, for example, by replacing h by
${{\mathbb{E}\!\left[{\frac{1}{\lambda^* - g(W)}} \right]}} = {C^{\prime}} < \infty$
, then either Condition C1 is satisfied in the first case but fails in the second case. However, in the second case, if the inequality is strict, condensation arises. Therefore, for fixed g, condensation in this model arises if we reduce h sufficiently pointwise, for example, by replacing h by \begin{equation*}{{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^* - g(W)}} \right]}} > 1 \quad \text{ or } \quad {{\mathbb{E} \!\left[{\frac{h(W)}{\lambda^* - g(W)}} \right]}} \leq 1.\end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\frac{h(W)}{\lambda^* - g(W)}} \right]}} > 1 \quad \text{ or } \quad {{\mathbb{E} \!\left[{\frac{h(W)}{\lambda^* - g(W)}} \right]}} \leq 1.\end{equation*}
 $K \cdot h$
where
$K \cdot h$
where
 $K < 1/{C^{\prime}}$
is a constant.
$K < 1/{C^{\prime}}$
is a constant.
-
3. Informally, if one considers h to be a factor representing ‘initial popularity’ and g to be a factor representing ‘reinforcement’, the condensation occurs around nodes of maximum ‘reinforcement’, rather than those of maximal ‘initial popularity’. It may even be the case, for example, that h is minimised on the sets
 $\mathcal{M}_{\varepsilon}$
where the condensation occurs.
$\mathcal{M}_{\varepsilon}$
where the condensation occurs.
3.2.3. A coupling lemma
In order to prove Theorem 3.1, we first prove an additional lemma. For each
![]() $\varepsilon > 0$
such that
$\varepsilon > 0$
such that
![]() $\varepsilon < \lambda^*$
, let
$\varepsilon < \lambda^*$
, let
![]() ${\mathcal{T}}^{+\varepsilon} = ({\mathcal{T}}^{+\varepsilon}_{t})_{t \geq 0}$
and
${\mathcal{T}}^{+\varepsilon} = ({\mathcal{T}}^{+\varepsilon}_{t})_{t \geq 0}$
and
![]() ${\mathcal{T}}^{-\varepsilon} = ({\mathcal{T}}^{-\varepsilon}_{t})_{t \geq 0}$
denote GPAF-trees with the same set of weights, but with the function g modified to
${\mathcal{T}}^{-\varepsilon} = ({\mathcal{T}}^{-\varepsilon}_{t})_{t \geq 0}$
denote GPAF-trees with the same set of weights, but with the function g modified to
![]() $g_{+\varepsilon}$
and
$g_{+\varepsilon}$
and
![]() $g_{-\varepsilon}$
respectively, on the set
$g_{-\varepsilon}$
respectively, on the set
![]() $\mathcal{M}_{\varepsilon}$
from (26), with
$\mathcal{M}_{\varepsilon}$
from (26), with
The motivation behind these choices of
![]() ${\mathcal{T}}^{+\varepsilon}$
and
${\mathcal{T}}^{+\varepsilon}$
and
![]() ${\mathcal{T}}^{-\varepsilon}$
is that, because
${\mathcal{T}}^{-\varepsilon}$
is that, because
![]() ${\mathcal{T}}$
does not satisfy Condition C1,
${\mathcal{T}}$
does not satisfy Condition C1,
![]() $g_{+\varepsilon}$
and
$g_{+\varepsilon}$
and
![]() $g_{-\varepsilon}$
attain their essential suprema on sets of positive measure. Thus, because
$g_{-\varepsilon}$
attain their essential suprema on sets of positive measure. Thus, because
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, by Remark 3.1 these auxiliary trees satisfy Condition C1, and we may apply the theorems from Section 2 with regard to these trees. Then, using the fact that these trees provide sufficiently good ‘approximations’ of the tree
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, by Remark 3.1 these auxiliary trees satisfy Condition C1, and we may apply the theorems from Section 2 with regard to these trees. Then, using the fact that these trees provide sufficiently good ‘approximations’ of the tree
![]() ${\mathcal{T}}$
, we may deduce our results by sending
${\mathcal{T}}$
, we may deduce our results by sending
![]() $\varepsilon$
to 0.
$\varepsilon$
to 0.
In this vein, let
![]() $N^{+\varepsilon}_{\geq k}(t,B)$
,
$N^{+\varepsilon}_{\geq k}(t,B)$
,
![]() $N_{\geq k}(t,B)$
, and
$N_{\geq k}(t,B)$
, and
![]() $N^{-\varepsilon}_{\geq k}(t,B)$
denote the number of vertices with out-degree
$N^{-\varepsilon}_{\geq k}(t,B)$
denote the number of vertices with out-degree
![]() $\geq k$
and weight belonging to the set B in
$\geq k$
and weight belonging to the set B in
![]() ${\mathcal{T}}^{+\varepsilon}_{t}$
,
${\mathcal{T}}^{+\varepsilon}_{t}$
,
![]() ${\mathcal{T}}_{t}$
, and
${\mathcal{T}}_{t}$
, and
![]() ${\mathcal{T}}^{-\varepsilon}_t$
, respectively. In their respective trees, we also denote by
${\mathcal{T}}^{-\varepsilon}_t$
, respectively. In their respective trees, we also denote by
![]() ${\mathcal{Z}}^{+\varepsilon}_t$
,
${\mathcal{Z}}^{+\varepsilon}_t$
,
![]() ${\mathcal{Z}}_t$
, and
${\mathcal{Z}}_t$
, and
![]() ${\mathcal{Z}}^{-\varepsilon}_t$
the partition functions at time t. Finally, for brevity, we write
${\mathcal{Z}}^{-\varepsilon}_t$
the partition functions at time t. Finally, for brevity, we write
![]() $f^{(+\varepsilon)}_{t}(v)$
,
$f^{(+\varepsilon)}_{t}(v)$
,
![]() $f_{t}(v)$
, and
$f_{t}(v)$
, and
![]() $f^{(-\varepsilon)}_{t}(v)$
for the fitness of a vertex v at time t in each of these models. For example,
$f^{(-\varepsilon)}_{t}(v)$
for the fitness of a vertex v at time t in each of these models. For example,
![]() $f_{t}(v) = g(W_v){\text{deg}^{+}({v, {\mathcal{T}}_{t}})} + h(W_v)$
.
$f_{t}(v) = g(W_v){\text{deg}^{+}({v, {\mathcal{T}}_{t}})} + h(W_v)$
.
Lemma 3.1. For every
![]() $\varepsilon > 0$
, there exists a coupling
$\varepsilon > 0$
, there exists a coupling
![]() $(\hat{{\mathcal{T}}}^{+\varepsilon}, \hat{{\mathcal{T}}}, \hat{{\mathcal{T}}}^{-\varepsilon})$
of these processes such that, on the coupling, for all
$(\hat{{\mathcal{T}}}^{+\varepsilon}, \hat{{\mathcal{T}}}, \hat{{\mathcal{T}}}^{-\varepsilon})$
of these processes such that, on the coupling, for all
![]() $t \in \mathbb{N}_0$
, the following hold:
$t \in \mathbb{N}_0$
, the following hold:
-
1. For all measurable sets
 $B \subseteq \mathcal{M}_{\varepsilon}^{c}$
we have
$B \subseteq \mathcal{M}_{\varepsilon}^{c}$
we have
 $\Xi^{+\varepsilon}(t,B) \leq \Xi(t,B) \leq \Xi^{-\varepsilon}(t,B)$
.
$\Xi^{+\varepsilon}(t,B) \leq \Xi(t,B) \leq \Xi^{-\varepsilon}(t,B)$
. -
2. For all measurable sets
 $B \subseteq \mathcal{M}_{\varepsilon}^{c}$
and
$B \subseteq \mathcal{M}_{\varepsilon}^{c}$
and
 $k \in \mathbb{N}_0$
, we have
$k \in \mathbb{N}_0$
, we have  \begin{equation*}N^{+\varepsilon}_{\geq k}(t,B) \leq N_{\geq k} (t,B) \leq N^{-\varepsilon}_{\geq k}(t,B).\end{equation*}
\begin{equation*}N^{+\varepsilon}_{\geq k}(t,B) \leq N_{\geq k} (t,B) \leq N^{-\varepsilon}_{\geq k}(t,B).\end{equation*}
-
3. We have the inequalities
 ${\mathcal{Z}}^{-\varepsilon}_{t} \leq {\mathcal{Z}}_t \leq {\mathcal{Z}}^{+\varepsilon}_t.$
${\mathcal{Z}}^{-\varepsilon}_{t} \leq {\mathcal{Z}}_t \leq {\mathcal{Z}}^{+\varepsilon}_t.$
Proof of Lemma
3.1. We construct the trees having the same sequence of weights
![]() $(W_{i})_{i \geq 0}$
, so that the dynamics of the models are only influenced by differences in the function g in the respective models. Thus, at time 0 each model consists of a single vertex labelled 0 with weight
$(W_{i})_{i \geq 0}$
, so that the dynamics of the models are only influenced by differences in the function g in the respective models. Thus, at time 0 each model consists of a single vertex labelled 0 with weight
![]() $W_0$
and having fitness given by
$W_0$
and having fitness given by
![]() $h(W_0)$
. Assume, that at the tth time-step,
$h(W_0)$
. Assume, that at the tth time-step,
In addition, assume, by induction, that we have
![]() ${\mathcal{Z}}^{-\varepsilon}_{t} \leq {\mathcal{Z}}_t \leq {\mathcal{Z}}^{+\varepsilon}_t$
and for each vertex v with
${\mathcal{Z}}^{-\varepsilon}_{t} \leq {\mathcal{Z}}_t \leq {\mathcal{Z}}^{+\varepsilon}_t$
and for each vertex v with
![]() $W_{v} \in \mathcal{M}^{c}_{\varepsilon}$
$W_{v} \in \mathcal{M}^{c}_{\varepsilon}$
Note that (27) and the fact that the trees have the same number of directed edges imply the first and the second assertions of the lemma up to time t. As a result, for each vertex v with
![]() $W_{v} \in \mathcal{M}^{c}_\varepsilon$
we have
$W_{v} \in \mathcal{M}^{c}_\varepsilon$
we have
![]() $f^{(+\varepsilon)}_t(v) \leq f_t(v) \leq f^{(-\varepsilon)}_{t}(v)$
. Now, for the
$f^{(+\varepsilon)}_t(v) \leq f_t(v) \leq f^{(-\varepsilon)}_{t}(v)$
. Now, for the
![]() $(t+1)$
th step, we do the following:
$(t+1)$
th step, we do the following:
Introduce a vertex
 $t+1$
with weight
$t+1$
with weight
 $W_{t+1}$
sampled independently from
$W_{t+1}$
sampled independently from
 $\mu$
.
$\mu$
.Form
 $\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1}$
by sampling the parent v of
$\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1}$
by sampling the parent v of
 $t+1$
independently according to the law of
$t+1$
independently according to the law of
 $\mathcal{T}^{-\varepsilon}$
, i.e., with probability proportional to
$\mathcal{T}^{-\varepsilon}$
, i.e., with probability proportional to
 $f^{(-\varepsilon)}_t(v)$
. Then, in order to form
$f^{(-\varepsilon)}_t(v)$
. Then, in order to form
 $\hat{{\mathcal{T}}}_{t+1}$
, sample an independent uniformly distributed random variable
$\hat{{\mathcal{T}}}_{t+1}$
, sample an independent uniformly distributed random variable
 $U_1$
on [0, 1].
$U_1$
on [0, 1].
If
and \begin{equation*}U_1 \leq \frac{{\mathcal{Z}}^{-\varepsilon}_{t}f_{t}(v) }{{\mathcal{Z}}_t f^{(-\varepsilon)}_{t}(v)}\end{equation*}
\begin{equation*}U_1 \leq \frac{{\mathcal{Z}}^{-\varepsilon}_{t}f_{t}(v) }{{\mathcal{Z}}_t f^{(-\varepsilon)}_{t}(v)}\end{equation*}
 $W_{v} \in \mathcal{M}_{\varepsilon}^{c}$
, select v as the parent of
$W_{v} \in \mathcal{M}_{\varepsilon}^{c}$
, select v as the parent of
 $t+1$
in
$t+1$
in
 $\hat{{\mathcal{T}}}_{t+1}$
as well.
$\hat{{\mathcal{T}}}_{t+1}$
as well.
Otherwise, form
 $\hat{{\mathcal{T}}}_{t+1}$
by selecting the parent v
′ of
$\hat{{\mathcal{T}}}_{t+1}$
by selecting the parent v
′ of
 $t+1$
with probability proportional to
$t+1$
with probability proportional to
 $f_{t}(v^{\prime})$
out of all the vertices with weight
$f_{t}(v^{\prime})$
out of all the vertices with weight
 $W_{v^{\prime}} \in \mathcal{M}_{\varepsilon}$
.
$W_{v^{\prime}} \in \mathcal{M}_{\varepsilon}$
.
Then form
 $\hat{{\mathcal{T}}}^{+\varepsilon}_{t+1}$
from
$\hat{{\mathcal{T}}}^{+\varepsilon}_{t+1}$
from
 $\hat{{\mathcal{T}}}_{t+1}$
in an identical manner to the way
$\hat{{\mathcal{T}}}_{t+1}$
in an identical manner to the way
 $\hat{{\mathcal{T}}}_{t+1}$
is formed from
$\hat{{\mathcal{T}}}_{t+1}$
is formed from
 $\hat{{\mathcal{T}}}^{-\varepsilon}$
, with another, independent uniform random variable
$\hat{{\mathcal{T}}}^{-\varepsilon}$
, with another, independent uniform random variable
 $U_2$
on [0, 1].
$U_2$
on [0, 1].
It is clear that
![]() $\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1} \sim {\mathcal{T}}^{-\varepsilon}_{t+1}$
. On the other hand, in
$\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1} \sim {\mathcal{T}}^{-\varepsilon}_{t+1}$
. On the other hand, in
![]() $\hat{{\mathcal{T}}}_{t+1}$
the probability of choosing a parent v of
$\hat{{\mathcal{T}}}_{t+1}$
the probability of choosing a parent v of
![]() $t+1$
with weight
$t+1$
with weight
![]() $W_v \in \mathcal{M}_{\varepsilon}^{c}$
is
$W_v \in \mathcal{M}_{\varepsilon}^{c}$
is
whilst the probability of choosing a parent v
′ with weight
![]() $W_{v^{\prime}} \in \mathcal{M}_{\varepsilon}$
is
$W_{v^{\prime}} \in \mathcal{M}_{\varepsilon}$
is
 \begin{align*}& \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(\sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon}\left(1- \frac{{\mathcal{Z}}^{-\varepsilon}_{t}f_{t}(v)}{{\mathcal{Z}}_t f^{(-\varepsilon)}_{t}(v)}\right) \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}\right) \\ & \qquad + \frac{f_t(v^{\prime})}{\sum_{v\,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(\sum_{v\,:\,W_v \geq {w^{*}} - \varepsilon} \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}\right)\\& = \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)}\left(\sum_{v} \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}- \sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon} \frac{f_{t}(v)}{{\mathcal{Z}}_t} \right)\\& = \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(1 - \frac{\sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon}f_{t}(v)}{{\mathcal{Z}}_t}\right) = \frac{f_t(v^{\prime})}{{\mathcal{Z}}_t},\end{align*}
\begin{align*}& \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(\sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon}\left(1- \frac{{\mathcal{Z}}^{-\varepsilon}_{t}f_{t}(v)}{{\mathcal{Z}}_t f^{(-\varepsilon)}_{t}(v)}\right) \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}\right) \\ & \qquad + \frac{f_t(v^{\prime})}{\sum_{v\,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(\sum_{v\,:\,W_v \geq {w^{*}} - \varepsilon} \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}\right)\\& = \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)}\left(\sum_{v} \frac{f^{(-\varepsilon)}_t(v)}{{\mathcal{Z}}^{-\varepsilon}_t}- \sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon} \frac{f_{t}(v)}{{\mathcal{Z}}_t} \right)\\& = \frac{f_t(v^{\prime})}{\sum_{v \,:\,W_{v} \geq {w^{*}} - \varepsilon} f_{t}(v)} \left(1 - \frac{\sum_{v\,:\, W_{v} < {w^{*}} - \varepsilon}f_{t}(v)}{{\mathcal{Z}}_t}\right) = \frac{f_t(v^{\prime})}{{\mathcal{Z}}_t},\end{align*}
where we use the fact that
![]() $\sum_{v} f_{t}(v) = {\mathcal{Z}}_t$
. Thus, we have
$\sum_{v} f_{t}(v) = {\mathcal{Z}}_t$
. Thus, we have
![]() $\hat{{\mathcal{T}}}_{t+1} \sim {\mathcal{T}}_{t+1}$
. Moreover, either the same vertex is chosen as the parent of
$\hat{{\mathcal{T}}}_{t+1} \sim {\mathcal{T}}_{t+1}$
. Moreover, either the same vertex is chosen as the parent of
![]() $t+1$
in both
$t+1$
in both
![]() $\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1}$
and
$\hat{{\mathcal{T}}}^{-\varepsilon}_{t+1}$
and
![]() $\hat{{\mathcal{T}}}_{t+1}$
, or a vertex of weight belonging to
$\hat{{\mathcal{T}}}_{t+1}$
, or a vertex of weight belonging to
![]() $\mathcal{M}_{\varepsilon}$
is chosen as the parent of
$\mathcal{M}_{\varepsilon}$
is chosen as the parent of
![]() $t+1$
in
$t+1$
in
![]() $\hat{\mathcal{T}}_{t+1}$
. This implies the left inequality in (27); in addition, when combined with the fact that
$\hat{\mathcal{T}}_{t+1}$
. This implies the left inequality in (27); in addition, when combined with the fact that
![]() $g_{-\varepsilon}(W_{t+1}) \leq g(W_{t+1})$
, it guarantees that
$g_{-\varepsilon}(W_{t+1}) \leq g(W_{t+1})$
, it guarantees that
![]() ${\mathcal{Z}}^{-\varepsilon}_{t+1} \leq {\mathcal{Z}}_{t+1}$
. The proofs of the fact that
${\mathcal{Z}}^{-\varepsilon}_{t+1} \leq {\mathcal{Z}}_{t+1}$
. The proofs of the fact that
![]() $\hat{{\mathcal{T}}}^{+\varepsilon}_{t+1} \sim {\mathcal{T}}^{+\varepsilon}_{t+1}$
, the right inequality in (27), and the fact that
$\hat{{\mathcal{T}}}^{+\varepsilon}_{t+1} \sim {\mathcal{T}}^{+\varepsilon}_{t+1}$
, the right inequality in (27), and the fact that
![]() ${\mathcal{Z}}_{t+1} \leq {\mathcal{Z}}^{+\varepsilon}_{t+1}$
are similar, so we may thus iterate the coupling.
${\mathcal{Z}}_{t+1} \leq {\mathcal{Z}}^{+\varepsilon}_{t+1}$
are similar, so we may thus iterate the coupling.
3.2.4. Proof of Theorem 3.1
In order to prove Theorem 3.1, we use the auxiliary GPAF-trees
![]() ${\mathcal{T}}^{+\varepsilon}$
and
${\mathcal{T}}^{+\varepsilon}$
and
![]() ${\mathcal{T}}^{-\varepsilon}$
according to Lemma 3.1.
${\mathcal{T}}^{-\varepsilon}$
according to Lemma 3.1.
Proof of Theorem
3.1. For the first assertion, suppose that B is measurable, with
![]() $B \subseteq \mathcal{M}^{c}_{\varepsilon}$
. Then, if we define the corresponding quantities
$B \subseteq \mathcal{M}^{c}_{\varepsilon}$
. Then, if we define the corresponding quantities
![]() $\Xi^{+\varepsilon}(t,\cdot)$
,
$\Xi^{+\varepsilon}(t,\cdot)$
,
![]() $\Xi^{-\varepsilon}(t,\cdot)$
associated with
$\Xi^{-\varepsilon}(t,\cdot)$
associated with
![]() ${\mathcal{T}}^{+\varepsilon}$
and
${\mathcal{T}}^{+\varepsilon}$
and
![]() ${\mathcal{T}}^{-\varepsilon}$
, from the coupling in Lemma 3.1, we have
${\mathcal{T}}^{-\varepsilon}$
, from the coupling in Lemma 3.1, we have
Recall that the auxiliary trees
![]() ${\mathcal{T}}^{+\varepsilon}$
and
${\mathcal{T}}^{+\varepsilon}$
and
![]() ${\mathcal{T}}^{-\varepsilon}$
have associated functions
${\mathcal{T}}^{-\varepsilon}$
have associated functions
![]() $g_{+\varepsilon}$
and
$g_{+\varepsilon}$
and
![]() $g_{-\varepsilon}$
which attain their maxima on a set of positive measure and thus satisfy Condition C1, with Malthusian parameters
$g_{-\varepsilon}$
which attain their maxima on a set of positive measure and thus satisfy Condition C1, with Malthusian parameters
![]() $\alpha^{(+\varepsilon)} > \lambda^{*}$
and
$\alpha^{(+\varepsilon)} > \lambda^{*}$
and
![]() $\alpha^{(-\varepsilon)} > \lambda^{*} - \varepsilon$
. Moreover, note that, by the definition of
$\alpha^{(-\varepsilon)} > \lambda^{*} - \varepsilon$
. Moreover, note that, by the definition of
![]() $g_{-\varepsilon}$
,
$g_{-\varepsilon}$
,
so that, recalling (23),
![]() $\alpha^{(-\varepsilon)} \leq \lambda^*$
. As a result,
$\alpha^{(-\varepsilon)} \leq \lambda^*$
. As a result,
![]() $\lambda^* - \varepsilon < \alpha^{(-\varepsilon)} \leq \lambda^*$
, so
$\lambda^* - \varepsilon < \alpha^{(-\varepsilon)} \leq \lambda^*$
, so
![]() $\lim_{\varepsilon \downarrow 0} \alpha^{(-\varepsilon)} = \lambda^*$
. Thus, by Lemma 3.1, Theorem 2.2, and dominated convergence, almost surely we have
$\lim_{\varepsilon \downarrow 0} \alpha^{(-\varepsilon)} = \lambda^*$
. Thus, by Lemma 3.1, Theorem 2.2, and dominated convergence, almost surely we have
Now, we also have
![]() $\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \lambda^{*}$
. Indeed, suppose for the sake of contradiction that
$\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \lambda^{*}$
. Indeed, suppose for the sake of contradiction that
![]() $\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \alpha^{\prime} > \lambda^{*}$
. Then, because
$\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \alpha^{\prime} > \lambda^{*}$
. Then, because
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, by dominated convergence we have
${{\mathbb{E}\!\left[{h(W)} \right]}} < \infty$
, by dominated convergence we have
But then, (23) is satisfied for
![]() $\lambda$
such that
$\lambda$
such that
![]() $\lambda^{*} < \lambda < \alpha^{\prime}$
, contradicting the assumption that Condition C1 fails for
$\lambda^{*} < \lambda < \alpha^{\prime}$
, contradicting the assumption that Condition C1 fails for
![]() ${\mathcal{T}}$
.
${\mathcal{T}}$
.
It follows that
![]() $\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \lambda^{*}$
, and thus, by Lemma 3.1 and dominated convergence, almost surely we have
$\lim_{\varepsilon \to 0} \alpha^{(+\varepsilon)} = \lambda^{*}$
, and thus, by Lemma 3.1 and dominated convergence, almost surely we have
The first assertion follows.
For the second assertion, given a measurable set B, for each
![]() $\varepsilon > 0$
, set
$\varepsilon > 0$
, set
![]() $B^{\varepsilon}\,:\!=\, B \cap \mathcal{M}_{\varepsilon}$
. Then, by Lemma 3.1, almost surely we have
$B^{\varepsilon}\,:\!=\, B \cap \mathcal{M}_{\varepsilon}$
. Then, by Lemma 3.1, almost surely we have
 \begin{align*}\limsup_{t \to \infty} \frac{N_{\geq k} (t, B)}{t} & \leq \liminf_{\varepsilon \to 0} \left({{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g_{-\varepsilon}(W)i + h(W)}{g_{-\varepsilon}(W)i + h(W) + \alpha^{(-\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)} \right]}}+ \mu(\mathcal{M}_{\varepsilon})\right)\\ & = \liminf_{\varepsilon \to 0} {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \alpha^{(-\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)} \right]}}\\ & = {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \lambda^{*}}\mathbf{1}_{B}(W)} \right]}}.\end{align*}
\begin{align*}\limsup_{t \to \infty} \frac{N_{\geq k} (t, B)}{t} & \leq \liminf_{\varepsilon \to 0} \left({{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g_{-\varepsilon}(W)i + h(W)}{g_{-\varepsilon}(W)i + h(W) + \alpha^{(-\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)} \right]}}+ \mu(\mathcal{M}_{\varepsilon})\right)\\ & = \liminf_{\varepsilon \to 0} {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \alpha^{(-\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)} \right]}}\\ & = {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g(W)i + h(W)}{g(W)i + h(W) + \lambda^{*}}\mathbf{1}_{B}(W)} \right]}}.\end{align*}
Similarly, almost surely,
 \begin{align*}\liminf_{t \to \infty} \frac{N_{\geq k} (t, B)}{t} & \geq \limsup_{\varepsilon \to 0} {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g_{+\varepsilon}(W)i + h(W)}{g_{+\varepsilon}(W)i + h(W) + \alpha^{(+\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)}\right]}} \\ & = \limsup_{\varepsilon \to 0} \mathbb{E}\!\left[\prod_{i=0}^{k-1} \frac{g(W)i + h(W))}{g(W)i + h(W) + \alpha^{(+\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)\right] \\ & = \mathbb{E}\!\left[\prod_{i=0}^{k-1} \frac{g(W)i + h(W))}{g(W)i + h(W) + \lambda^{*}}\mathbf{1}_{B}(W)\right] .\end{align*}
\begin{align*}\liminf_{t \to \infty} \frac{N_{\geq k} (t, B)}{t} & \geq \limsup_{\varepsilon \to 0} {{\mathbb{E}\!\left[{\prod_{i=0}^{k-1} \frac{g_{+\varepsilon}(W)i + h(W)}{g_{+\varepsilon}(W)i + h(W) + \alpha^{(+\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)}\right]}} \\ & = \limsup_{\varepsilon \to 0} \mathbb{E}\!\left[\prod_{i=0}^{k-1} \frac{g(W)i + h(W))}{g(W)i + h(W) + \alpha^{(+\varepsilon)}} \mathbf{1}_{B^{\varepsilon}}(W)\right] \\ & = \mathbb{E}\!\left[\prod_{i=0}^{k-1} \frac{g(W)i + h(W))}{g(W)i + h(W) + \lambda^{*}}\mathbf{1}_{B}(W)\right] .\end{align*}
Finally, for the last assertion, by Lemma 3.1, for each
![]() $t \in \mathbb{N}_0$
we have
$t \in \mathbb{N}_0$
we have
Taking limits as t goes to infinity and applying Theorem 2.4, the result follows similarly to the previous assertions.
3.3. Degenerate degrees in the GPAF-tree when Condition C1 fails
In this subsection, we show that if the GPAF-tree fails to satisfy Condition
![]() ${\textbf{C1}}$
by having
${\textbf{C1}}$
by having
![]() $m(\lambda, \mathbb{R}_{+}) = \infty$
for all
$m(\lambda, \mathbb{R}_{+}) = \infty$
for all
![]() $\lambda > 0$
, almost surely the proportion of vertices that are leaves tends to 1. Consequently, the limiting mass of edges ‘escapes to infinity’, as described in Theorem 3.2 below. Note that Condition C1 fails in this manner in the GPAF tree if
$\lambda > 0$
, almost surely the proportion of vertices that are leaves tends to 1. Consequently, the limiting mass of edges ‘escapes to infinity’, as described in Theorem 3.2 below. Note that Condition C1 fails in this manner in the GPAF tree if
![]() $\text{ess sup}{(g)} = \infty$
or
$\text{ess sup}{(g)} = \infty$
or
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} = \infty$
. We remark that results similar to Theorem 3.2 have been shown in preferential attachment models with multiplicative fitness with
${{\mathbb{E}\!\left[{h(W)} \right]}} = \infty$
. We remark that results similar to Theorem 3.2 have been shown in preferential attachment models with multiplicative fitness with
![]() $\mu$
having finite support [Reference Borgs, Chayes, Daskalakis and Roch8, Theorem 6] and preferential attachment models with additive fitness (the extreme disorder regime in [Reference Lodewijks and Ortgiese23, Theorem 2.6]). These cases correspond to
$\mu$
having finite support [Reference Borgs, Chayes, Daskalakis and Roch8, Theorem 6] and preferential attachment models with additive fitness (the extreme disorder regime in [Reference Lodewijks and Ortgiese23, Theorem 2.6]). These cases correspond to
![]() $h(x) \equiv 0$
and
$h(x) \equiv 0$
and
![]() $g(x) \equiv 1$
, respectively. In a similar vein to the start of Section 3.2.1, in this section we will require the following families of sets: for each
$g(x) \equiv 1$
, respectively. In a similar vein to the start of Section 3.2.1, in this section we will require the following families of sets: for each
![]() $m \in \mathbb{N}$
, we set
$m \in \mathbb{N}$
, we set
Theorem 3.2. Suppose
![]() ${\mathcal{T}} = ({\mathcal{T}}_{t})_{t \geq 0}$
is a GPAF-tree, with associated functions g,h, such that
${\mathcal{T}} = ({\mathcal{T}}_{t})_{t \geq 0}$
is a GPAF-tree, with associated functions g,h, such that
![]() $\text{ess sup}{(g)} = \infty$
or
$\text{ess sup}{(g)} = \infty$
or
![]() ${{\mathbb{E}\!\left[{h(W)}\right]}} = \infty$
. Then we have the following assertions:
${{\mathbb{E}\!\left[{h(W)}\right]}} = \infty$
. Then we have the following assertions:
-
1. For any measurable set B such that for some
 $m^{\prime} \in \mathbb{N}$
we have
$m^{\prime} \in \mathbb{N}$
we have
 $B \subseteq \mathscr{M}^{c}_{m^{\prime}}$
,
$B \subseteq \mathscr{M}^{c}_{m^{\prime}}$
,  \begin{equation*}\frac{\Xi(t,B)}{t} \xrightarrow{t \to \infty} 0, \quad {almost\ surely.}\end{equation*}
\begin{equation*}\frac{\Xi(t,B)}{t} \xrightarrow{t \to \infty} 0, \quad {almost\ surely.}\end{equation*}
-
2. For any measurable set
 $B \subseteq \mathbb{R}_{+}$
, we have
$B \subseteq \mathbb{R}_{+}$
, we have  \begin{equation*} \frac{N_0(t, B)}{t} \xrightarrow{t \to \infty} \mu(B), \quad {almost\ surely.}\end{equation*}
\begin{equation*} \frac{N_0(t, B)}{t} \xrightarrow{t \to \infty} \mu(B), \quad {almost\ surely.}\end{equation*}
-
3. The partition function satisfies
 \begin{equation*}\frac{{\mathcal{Z}}_{t}}{t} \xrightarrow{t \to \infty} \infty, \quad {almost\ surely.} \end{equation*}
\begin{equation*}\frac{{\mathcal{Z}}_{t}}{t} \xrightarrow{t \to \infty} \infty, \quad {almost\ surely.} \end{equation*}
Proof. This is similar to the proof of Theorem 3.1; however, we require some different notation. For each
![]() $m \in \mathbb{N}$
, let
$m \in \mathbb{N}$
, let
![]() ${\mathcal{T}}^{m} = ({\mathcal{T}}^{m}_{t})_{t \geq 0}$
and
${\mathcal{T}}^{m} = ({\mathcal{T}}^{m}_{t})_{t \geq 0}$
and
![]() ${\mathcal{T}}^{m,m} = ({\mathcal{T}}^{m,m}_{t \geq 0})$
denote analogues of the tree process modified on the sets
${\mathcal{T}}^{m,m} = ({\mathcal{T}}^{m,m}_{t \geq 0})$
denote analogues of the tree process modified on the sets
![]() $\mathscr{G}_{m}$
and
$\mathscr{G}_{m}$
and
![]() $\mathscr{H}_{m}$
. In particular, if we define
$\mathscr{H}_{m}$
. In particular, if we define
![]() $g_{m}, h_{m}$
so that
$g_{m}, h_{m}$
so that
we define
![]() ${\mathcal{T}}^{m}$
with the associated functions
${\mathcal{T}}^{m}$
with the associated functions
![]() $g_{m}, h$
, and
$g_{m}, h$
, and
![]() ${\mathcal{T}}^{m,m}$
with the associated functions
${\mathcal{T}}^{m,m}$
with the associated functions
![]() $g_{m}, h_{m}$
. Then, by mimicking the approach from the coupling in Lemma 3.1, for each
$g_{m}, h_{m}$
. Then, by mimicking the approach from the coupling in Lemma 3.1, for each
![]() $m \in \mathbb{N}$
we may couple the processes
$m \in \mathbb{N}$
we may couple the processes
![]() $(\hat{{\mathcal{T}}}^{m,m}, \hat{{\mathcal{T}}}^{m}, \hat{{\mathcal{T}}})$
so that, for all
$(\hat{{\mathcal{T}}}^{m,m}, \hat{{\mathcal{T}}}^{m}, \hat{{\mathcal{T}}})$
so that, for all
![]() $t \in \mathbb{N}_0$
, their respective partition functions satisfy
$t \in \mathbb{N}_0$
, their respective partition functions satisfy
![]() ${\mathcal{Z}}^{m,m}_{t} \leq {\mathcal{Z}}^{m}_{t} \leq {\mathcal{Z}}_{t}$
; for each vertex v
′ with
${\mathcal{Z}}^{m,m}_{t} \leq {\mathcal{Z}}^{m}_{t} \leq {\mathcal{Z}}_{t}$
; for each vertex v
′ with
![]() $W_{v^{\prime}} \in \mathscr{H}_{m}^{c}$
,
$W_{v^{\prime}} \in \mathscr{H}_{m}^{c}$
,
and for each vertex v with
![]() $W_v \in \mathscr{G}_{m}^{c}$
,
$W_v \in \mathscr{G}_{m}^{c}$
,
In this coupling, at each time-step t, one samples
![]() $\hat{{\mathcal{T}}}^{m,m}_t$
first, uses this (with another uniformly distributed random variable) to construct
$\hat{{\mathcal{T}}}^{m,m}_t$
first, uses this (with another uniformly distributed random variable) to construct
![]() $\hat{{\mathcal{T}}}^{m}_t$
, and then uses this to construct
$\hat{{\mathcal{T}}}^{m}_t$
, and then uses this to construct
![]() $\hat{{\mathcal{T}}}_{t}$
. Therefore, we have the following claim. For a measurable set B, let
$\hat{{\mathcal{T}}}_{t}$
. Therefore, we have the following claim. For a measurable set B, let
![]() $\Xi^{m,m}(t, B)$
and
$\Xi^{m,m}(t, B)$
and
![]() $N^{m,m}_{\geq k}(t,B)$
denote the counterparts of
$N^{m,m}_{\geq k}(t,B)$
denote the counterparts of
![]() $\Xi(t,B)$
and
$\Xi(t,B)$
and
![]() $N_{\geq k}(t,B)$
with respect to the tree
$N_{\geq k}(t,B)$
with respect to the tree
![]() ${\mathcal{T}}^{m,m}$
.
${\mathcal{T}}^{m,m}$
.
Claim 3.1. For all
![]() $m \in \mathbb{N}$
, there exists a coupling
$m \in \mathbb{N}$
, there exists a coupling
![]() $(\hat{{\mathcal{T}}}^{m,m}, \hat{{\mathcal{T}}})$
of
$(\hat{{\mathcal{T}}}^{m,m}, \hat{{\mathcal{T}}})$
of
![]() ${\mathcal{T}}^{m,m}$
and
${\mathcal{T}}^{m,m}$
and
![]() ${\mathcal{T}}$
such that, on the coupling, for all
${\mathcal{T}}$
such that, on the coupling, for all
![]() $t \in \mathbb{N}_{0}$
we have the following:
$t \in \mathbb{N}_{0}$
we have the following:
-
1. For all measurable sets
 $B \subseteq \mathscr{M}^{c}_{m}$
we have
$B \subseteq \mathscr{M}^{c}_{m}$
we have
 $\Xi(t, B) \leq \Xi^{m,m}(t, B)$
.
$\Xi(t, B) \leq \Xi^{m,m}(t, B)$
. -
2. For all measurable sets
 $B \subseteq \mathscr{M}^{c}_{m}$
and
$B \subseteq \mathscr{M}^{c}_{m}$
and
 $k \in \mathbb{N}_{0}$
we have
$k \in \mathbb{N}_{0}$
we have
 $N_{\geq k}(t, B) \leq N^{m,m}_{\geq k}(t,B)$
.
$N_{\geq k}(t, B) \leq N^{m,m}_{\geq k}(t,B)$
. -
3. We have the inequality
 ${\mathcal{Z}}^{m,m}_{t} \leq {\mathcal{Z}}_{t}$
.
${\mathcal{Z}}^{m,m}_{t} \leq {\mathcal{Z}}_{t}$
.
Now note that for all m sufficiently large,
![]() ${\mathcal{T}}^{m,m}$
satisfies C1. Indeed, if
${\mathcal{T}}^{m,m}$
satisfies C1. Indeed, if
![]() $\text{ess sup}{(g)} = \infty$
, then because
$\text{ess sup}{(g)} = \infty$
, then because
![]() ${{\mathbb{E}\!\left[{h_{m}(W)} \right]}} \leq m$
and
${{\mathbb{E}\!\left[{h_{m}(W)} \right]}} \leq m$
and
![]() $g_{m}$
attains its maximum m on a set of positive measure, this follows from Remark 3.1. Otherwise, for m sufficiently large we have
$g_{m}$
attains its maximum m on a set of positive measure, this follows from Remark 3.1. Otherwise, for m sufficiently large we have
![]() $g_{m} = g$
, and for any
$g_{m} = g$
, and for any
![]() $\lambda > \text{ess sup}{(g)}$
,
$\lambda > \text{ess sup}{(g)}$
,
Thus, making m larger if necessary, we have that C1 is satisfied for this choice of
![]() $\lambda$
. In either case, let
$\lambda$
. In either case, let
![]() $\alpha^{(m)}$
denote the Malthusian parameter associated with
$\alpha^{(m)}$
denote the Malthusian parameter associated with
![]() ${\mathcal{T}}^{m,m}$
. Then
${\mathcal{T}}^{m,m}$
. Then
![]() $\alpha^{(m)} > \text{ess sup}{(g_{m})}$
increases as m increases, and even if
$\alpha^{(m)} > \text{ess sup}{(g_{m})}$
increases as m increases, and even if
![]() $\text{ess sup}{(g_{m})} < \infty$
we must have
$\text{ess sup}{(g_{m})} < \infty$
we must have
Indeed, suppose this were not the case, and
![]() $\lim_{m \uparrow \infty} \alpha^{(m)} = \alpha^{\prime} < \infty$
. Then, by monotone convergence,
$\lim_{m \uparrow \infty} \alpha^{(m)} = \alpha^{\prime} < \infty$
. Then, by monotone convergence,
since
![]() ${{\mathbb{E}\!\left[{h(W)} \right]}} = \infty$
. Now, the assertions of Theorem 3.2 follow from the claim in a similar manner to the way the assertions of Theorem 3.1 follow from Lemma 3.1.
${{\mathbb{E}\!\left[{h(W)} \right]}} = \infty$
. Now, the assertions of Theorem 3.2 follow from the claim in a similar manner to the way the assertions of Theorem 3.1 follow from Lemma 3.1.
Now, as in the previous subsection, suppose that g and h are increasing, and
![]() ${{\text{Supp} \!\left( {\mu} \right)}} \subseteq [0,{w^{*}}]$
, where
${{\text{Supp} \!\left( {\mu} \right)}} \subseteq [0,{w^{*}}]$
, where
![]() ${w^{*}} \,:\!=\, \sup{\left({{\text{Supp} \left( {\mu} \right)}}\right)}$
. The proof of the following corollary is similar to that of Corollary 3.1, and we therefore again leave it to the reader.
${w^{*}} \,:\!=\, \sup{\left({{\text{Supp} \left( {\mu} \right)}}\right)}$
. The proof of the following corollary is similar to that of Corollary 3.1, and we therefore again leave it to the reader.
Corollary 3.2. Under the above assumptions, with regard to the weak topology,
4. Analysis of
 ${\left({\mu, f, \ell}\right)}$
-RIF trees assuming C2
${\left({\mu, f, \ell}\right)}$
-RIF trees assuming C2
By Theorem 2.4, under certain conditions on the fitness function f and C1, Condition C2 is satisfied, i.e.,
However, Theorem 3.1 shows that this condition may be satisfied despite Condition C1 failing. Therefore, in this in this section, we analyse the model under Condition C2. We state and prove Theorem 4.1 below and Theorem 4.2, leaving the details to the reader. These proofs rely on Proposition 4.1, proved in Section 4.3 and Section 4.4, and on Proposition 4.2, proved in Section 4.5.
4.1. Main results: convergence in probability of
 $N_{k}(n, B)/\ell n$
under C2
$N_{k}(n, B)/\ell n$
under C2
Theorem 4.1. Assume Condition C2. Then, for any measurable set B, we have
 \begin{equation*}\frac{N_{k}(t, B)}{\ell t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{\alpha}{f(k,W) + \alpha} \prod_{s=0}^{k-1} \frac{f(s,W)}{f(s,W) + \alpha} \mathbf{1}_{B}(W)} \right]}} = p^{\alpha}_{k}(B), \quad {in\ probability.}\end{equation*}
\begin{equation*}\frac{N_{k}(t, B)}{\ell t} \xrightarrow{t \to \infty} {{\mathbb{E}\!\left[{\frac{\alpha}{f(k,W) + \alpha} \prod_{s=0}^{k-1} \frac{f(s,W)}{f(s,W) + \alpha} \mathbf{1}_{B}(W)} \right]}} = p^{\alpha}_{k}(B), \quad {in\ probability.}\end{equation*}
In order to prove Theorem 4.1, we define the following family of sets:
We also require Proposition 4.1 and Proposition 4.2, proved in Section 4.4.1 and Section 4.5.1. These proofs rely on the results stated in Section 4.2 and Section 4.3.
Proposition 4.1. For any set
![]() $B\in {\mathscr{F}}$
, for each
$B\in {\mathscr{F}}$
, for each
![]() $k \in \mathbb{N}_0$
we have
$k \in \mathbb{N}_0$
we have
Proposition 4.2. For any
![]() $B \in {\mathscr{F}}$
and
$B \in {\mathscr{F}}$
and
![]() $k \in \mathbb{N}_0$
we have
$k \in \mathbb{N}_0$
we have
 \begin{equation*}\lim_{t \to \infty} {{\mathbb{E}\!\left[{\frac{\left(N_{k}(t, B)\right)^2}{\ell^2 t^2}}\right]}} = (p^{\alpha}_{k}(B))^2.\end{equation*}
\begin{equation*}\lim_{t \to \infty} {{\mathbb{E}\!\left[{\frac{\left(N_{k}(t, B)\right)^2}{\ell^2 t^2}}\right]}} = (p^{\alpha}_{k}(B))^2.\end{equation*}
Proof of Theorem
4.1. The result follows for all
![]() $B \in {\mathscr{F}}$
by combining Proposition 4.1 and Proposition 4.2 and applying Chebyshev’s inequality.
$B \in {\mathscr{F}}$
by combining Proposition 4.1 and Proposition 4.2 and applying Chebyshev’s inequality.
Now, let B be an arbitrary measurable set and let
![]() $\varepsilon > 0$
be given. Then, since for each
$\varepsilon > 0$
be given. Then, since for each
![]() $s \in \left\{1, \ldots, k\right\}$
the map
$s \in \left\{1, \ldots, k\right\}$
the map
![]() $w \mapsto f(s,w)$
is measurable, by Lusin’s theorem, we can find a compact set
$w \mapsto f(s,w)$
is measurable, by Lusin’s theorem, we can find a compact set
![]() $E \subseteq B$
such that
$E \subseteq B$
such that
![]() $\mu(B \cap E^{c}) < \varepsilon/3$
and for each
$\mu(B \cap E^{c}) < \varepsilon/3$
and for each
![]() $s \in \left\{1, \ldots, k\right\}$
the restriction of the map
$s \in \left\{1, \ldots, k\right\}$
the restriction of the map
![]() $w \mapsto f(s,w)$
to E is continuous. Moreover, note that
$w \mapsto f(s,w)$
to E is continuous. Moreover, note that
![]() $p^{\alpha}_{k}(B) - p^{\alpha}_{k}(B \cap E) \leq \mu(B \cap E^{c}) < \varepsilon/3$
. Then,
$p^{\alpha}_{k}(B) - p^{\alpha}_{k}(B \cap E) \leq \mu(B \cap E^{c}) < \varepsilon/3$
. Then,
 \begin{align} \nonumber {{\mathbb{P}\!\left({\left|\frac{N_{k}(t,B)}{\ell t} - p^{\alpha}_{k}(B)\right| > \varepsilon}\right)}}& \leq \mathbb P \bigg(\bigg(\left|\frac{N_{k}(t,B)}{\ell t} - \frac{N_{k}(t,B\cap E)}{\ell t}\right|\\ \nonumber& \qquad \ + \left|\frac{N_{k}(t,B\cap E)}{\ell t} - p^{\alpha}_{k}(B\cap E)\right| \\ \nonumber & \qquad \ + \left|p^{\alpha}_{k}(B \cap E) - p^{\alpha}_{k}(B)\right|\bigg) > \varepsilon\bigg) \\ \nonumber & \leq {{\mathbb{P}\!\left({\left|\frac{N_{k}(t,B\cap E)}{\ell t} - p^{\alpha}_{k}(B\cap E)\right| > \varepsilon/3}\right)}}\\ & \quad + {{\mathbb{P}\!\left({\left|\frac{N_{k}(t, B)}{\ell t} - \frac{N_{k}(t, B \cap E)}{\ell t}\right| > \varepsilon/3}\right)}}.\end{align}
\begin{align} \nonumber {{\mathbb{P}\!\left({\left|\frac{N_{k}(t,B)}{\ell t} - p^{\alpha}_{k}(B)\right| > \varepsilon}\right)}}& \leq \mathbb P \bigg(\bigg(\left|\frac{N_{k}(t,B)}{\ell t} - \frac{N_{k}(t,B\cap E)}{\ell t}\right|\\ \nonumber& \qquad \ + \left|\frac{N_{k}(t,B\cap E)}{\ell t} - p^{\alpha}_{k}(B\cap E)\right| \\ \nonumber & \qquad \ + \left|p^{\alpha}_{k}(B \cap E) - p^{\alpha}_{k}(B)\right|\bigg) > \varepsilon\bigg) \\ \nonumber & \leq {{\mathbb{P}\!\left({\left|\frac{N_{k}(t,B\cap E)}{\ell t} - p^{\alpha}_{k}(B\cap E)\right| > \varepsilon/3}\right)}}\\ & \quad + {{\mathbb{P}\!\left({\left|\frac{N_{k}(t, B)}{\ell t} - \frac{N_{k}(t, B \cap E)}{\ell t}\right| > \varepsilon/3}\right)}}.\end{align}
Now, note that by the strong law of large numbers applied to
![]() $N_{\geq 0}(t,B \cap E^{c})/\ell t$
, i.e., the proportion of all vertices with weight belonging to
$N_{\geq 0}(t,B \cap E^{c})/\ell t$
, i.e., the proportion of all vertices with weight belonging to
![]() $B \cap E^{c}$
, and Egorov’s theorem, for any
$B \cap E^{c}$
, and Egorov’s theorem, for any
![]() $\delta > 0$
there exists an event G with
$\delta > 0$
there exists an event G with
![]() $\mathbb{P}(G) < \delta$
such that
$\mathbb{P}(G) < \delta$
such that
uniformly on the complement of G. Therefore, the result follows from (29), Proposition 4.1, and Proposition 4.2 by taking limits as t tends to infinity.
Using the approach to the upper bound for the mean in the next subsection, and applying Corollary 4.1 stated below with
![]() $k=1$
and
$k=1$
and
![]() $e_0, e_1 = 0$
, if
$e_0, e_1 = 0$
, if
![]() $N_{\geq 1}(t, B)$
denotes the number of vertices of out-degree at least 1 in the tree with weight belonging to B, we actually have
$N_{\geq 1}(t, B)$
denotes the number of vertices of out-degree at least 1 in the tree with weight belonging to B, we actually have
as long as
![]() $\liminf_{t \to \infty} \frac{{\mathcal{Z}}_{t}}{t} \geq \alpha^{\prime}$
. By sending
$\liminf_{t \to \infty} \frac{{\mathcal{Z}}_{t}}{t} \geq \alpha^{\prime}$
. By sending
![]() $\alpha^{\prime}$
to infinity, this yields the following analogue of Theorem 3.2.
$\alpha^{\prime}$
to infinity, this yields the following analogue of Theorem 3.2.
Theorem 4.2. Suppose
![]() ${\mathcal{T}}$
is a
${\mathcal{T}}$
is a
![]() ${\left({\mu, f, \ell}\right)}$
-RIF tree such that
${\left({\mu, f, \ell}\right)}$
-RIF tree such that
![]() $\lim_{t \to \infty} \frac{{\mathcal{Z}}_{t}}{t} = \infty$
. Then for any measurable set
$\lim_{t \to \infty} \frac{{\mathcal{Z}}_{t}}{t} = \infty$
. Then for any measurable set
![]() $B \subseteq [0,\infty)$
, we have
$B \subseteq [0,\infty)$
, we have
4.2. Summation arguments
Here we state some summation arguments required for the subsequent proofs. The following lemma and corollary are taken from [Reference Fountoulakis, Iyer, Mailler and Sulzbach17]. We include them here, with minor changes in notation, for completeness. For
![]() $e_0, \ldots, e_k \geq 0$
,
$e_0, \ldots, e_k \geq 0$
,
![]() $0 \leq \eta < 1$
, let
$0 \leq \eta < 1$
, let
 \begin{equation*}\mathcal{S}_t(e_0, \ldots, e_k, \eta) \,:\!=\, \frac{1}{t} \sum_{\eta t < i_0 < \cdots < i_k \leq t} \prod_{s=0}^{k-1}\left( \left(\frac{i_s}{i_{s+1}} \right)^{e_s} \cdot \frac{1}{i_{s+1} -1} \right) \left(\frac{i_k}{t} \right)^{e_k}.\end{equation*}
\begin{equation*}\mathcal{S}_t(e_0, \ldots, e_k, \eta) \,:\!=\, \frac{1}{t} \sum_{\eta t < i_0 < \cdots < i_k \leq t} \prod_{s=0}^{k-1}\left( \left(\frac{i_s}{i_{s+1}} \right)^{e_s} \cdot \frac{1}{i_{s+1} -1} \right) \left(\frac{i_k}{t} \right)^{e_k}.\end{equation*}
Lemma 4.1. ([Reference Fountoulakis, Iyer, Mailler and Sulzbach17, Lemma 4].) Uniformly in
![]() $e_0, \ldots, e_k \geq 0$
,
$e_0, \ldots, e_k \geq 0$
,
![]() $0 \leq \eta \leq 1/2$
, we have
$0 \leq \eta \leq 1/2$
, we have
 \begin{equation*}\mathcal{S}_t(e_0, \ldots, e_k, \eta) = \prod_{s=0}^{k} \frac{1}{e_s + 1} + \theta(\eta) + O \left(\frac{1}{t^{1/(k+2)}} + \frac{\sum_{s =0}^k e_s \log^{k+1}(t) }{t} \right).\end{equation*}
\begin{equation*}\mathcal{S}_t(e_0, \ldots, e_k, \eta) = \prod_{s=0}^{k} \frac{1}{e_s + 1} + \theta(\eta) + O \left(\frac{1}{t^{1/(k+2)}} + \frac{\sum_{s =0}^k e_s \log^{k+1}(t) }{t} \right).\end{equation*}
Here,
![]() $\theta(\eta)$
is a term satisfying
$\theta(\eta)$
is a term satisfying
![]() $ |\theta(\eta)| \leq M\eta^{1/(k+2)}$
for some universal constant M depending only on k.
$ |\theta(\eta)| \leq M\eta^{1/(k+2)}$
for some universal constant M depending only on k.
Corollary 4.1. ([Reference Fountoulakis, Iyer, Mailler and Sulzbach17, Corollary 5].) For
![]() $e_0, \ldots, e_k, f_0, \ldots, f_{k-1} \geq 0$
,
$e_0, \ldots, e_k, f_0, \ldots, f_{k-1} \geq 0$
,
![]() $0 \leq \eta \leq 1/2$
, we have
$0 \leq \eta \leq 1/2$
, we have
 \begin{align*}&\frac 1 t \sum_{\eta t < i_0\leq t} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} \prod_{s=0}^{k-1}\left( \left(\frac{i_s}{i_{s+1}} \right)^{e_s} \cdot \frac{f_{s}}{i_{s+1} -1} \right) \left(\frac{i_k}{t} \right)^{e_k}\\& \hspace {2cm} = \frac{1}{e_k +1}\prod_{s=0}^{k-1} \frac{f_{s}}{e_{s}+1} + \theta^{\prime}(\eta) + O \left(\frac{1}{t^{1/(k+2)}}\right).\end{align*}
\begin{align*}&\frac 1 t \sum_{\eta t < i_0\leq t} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} \prod_{s=0}^{k-1}\left( \left(\frac{i_s}{i_{s+1}} \right)^{e_s} \cdot \frac{f_{s}}{i_{s+1} -1} \right) \left(\frac{i_k}{t} \right)^{e_k}\\& \hspace {2cm} = \frac{1}{e_k +1}\prod_{s=0}^{k-1} \frac{f_{s}}{e_{s}+1} + \theta^{\prime}(\eta) + O \left(\frac{1}{t^{1/(k+2)}}\right).\end{align*}
Here,
![]() $\theta^{\prime}(\eta)$
is a term satisfying
$\theta^{\prime}(\eta)$
is a term satisfying
![]() $ |\theta^{\prime}(\eta)| \leq M^{\prime}\eta^{1/(k+2)}$
for some universal constant M′ depending only on k and
$ |\theta^{\prime}(\eta)| \leq M^{\prime}\eta^{1/(k+2)}$
for some universal constant M′ depending only on k and
![]() $f_0, \ldots, f_{k-1}$
, and the constant in the big-O term may depend on
$f_0, \ldots, f_{k-1}$
, and the constant in the big-O term may depend on
![]() $e_0, \ldots, e_{k}, f_0, \ldots, f_k$
.
$e_0, \ldots, e_{k}, f_0, \ldots, f_k$
.
4.3. Upper bound for the mean of
 $N_{k}(t,B)/\ell t$
$N_{k}(t,B)/\ell t$
In the following subsections, unless otherwise specified, we let B denote an arbitrary element of the family
![]() ${\mathscr{F}}$
defined in (4.1). Let
${\mathscr{F}}$
defined in (4.1). Let
![]() $N_{\eta, k}(t,B)$
be the number of vertices of degree
$N_{\eta, k}(t,B)$
be the number of vertices of degree
![]() $k \ell$
with weight in B that arrived after time
$k \ell$
with weight in B that arrived after time
![]() $\eta t$
. Then, since
$\eta t$
. Then, since
![]() $N_{\eta, k}(t,B) \leq N_{k}(t,B) \leq N_{\eta, k}(t,B) + \eta \ell t$
, we have
$N_{\eta, k}(t,B) \leq N_{k}(t,B) \leq N_{\eta, k}(t,B) + \eta \ell t$
, we have
Thus, to obtain an upper bound for the convergence of the mean, it suffices to prove that
In what follows, we use the notation
![]() $d_{i}(t)$
to denote the out-degree at time t of the vertex i born at time
$d_{i}(t)$
to denote the out-degree at time t of the vertex i born at time
![]() $i_0 \,:\!=\, \lfloor i/\ell \rfloor$
. We then have
$i_0 \,:\!=\, \lfloor i/\ell \rfloor$
. We then have
since the probability is identical for each of the
![]() $\ell$
vertices born at each time
$\ell$
vertices born at each time
![]() $i_0$
. In what follows, for a given i we denote by
$i_0$
. In what follows, for a given i we denote by
![]() $\mathcal{I}_{k} \,:\!=\, \{i_1, \ldots, i_k\}$
a collection of natural numbers
$\mathcal{I}_{k} \,:\!=\, \{i_1, \ldots, i_k\}$
a collection of natural numbers
![]() $i_0 < i_1 < \ldots < i_k \leq t$
. For ease of notation we exclude the dependence of
$i_0 < i_1 < \ldots < i_k \leq t$
. For ease of notation we exclude the dependence of
![]() $\mathcal{I}_{k}$
on i.
$\mathcal{I}_{k}$
on i.
For a natural number
![]() $s > i_0$
, we use the notation
$s > i_0$
, we use the notation
![]() $i {\rightarrow} s$
to denote that i is the vertex chosen at the sth time-step; hence i gains
$i {\rightarrow} s$
to denote that i is the vertex chosen at the sth time-step; hence i gains
![]() $\ell$
new neighbours at time s. Likewise, the notation
$\ell$
new neighbours at time s. Likewise, the notation
![]() $i {\not \rightarrow} s$
denotes that i is not chosen at the sth time-step. Then, let
$i {\not \rightarrow} s$
denotes that i is not chosen at the sth time-step. Then, let
![]() ${\mathcal{E}}_{i}({\mathcal{I}}_k, B)$
denote the event that
${\mathcal{E}}_{i}({\mathcal{I}}_k, B)$
denote the event that
![]() $W_i \in B$
and for all
$W_i \in B$
and for all
![]() $s \in \left\{i_0 +1, \ldots, t\right\}$
,
$s \in \left\{i_0 +1, \ldots, t\right\}$
,
![]() $i {\rightarrow} s$
if and only if
$i {\rightarrow} s$
if and only if
![]() $s \in {\mathcal{I}}_k$
. Clearly, we have
$s \in {\mathcal{I}}_k$
. Clearly, we have
 \begin{equation*}{{\mathbb{P}\!\left({d_{i}(t) = k, W_i \in B}\right)}} = \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\!\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B)}\right)}},\end{equation*}
\begin{equation*}{{\mathbb{P}\!\left({d_{i}(t) = k, W_i \in B}\right)}} = \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\!\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B)}\right)}},\end{equation*}
where
![]() $\tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
denotes the set of all subsets of
$\tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
denotes the set of all subsets of
![]() $\left\{i_0 +1, \ldots, t\right\}$
of size k. For
$\left\{i_0 +1, \ldots, t\right\}$
of size k. For
![]() $\varepsilon > 0$
and
$\varepsilon > 0$
and
![]() $t \geq 0$
and natural numbers
$t \geq 0$
and natural numbers
![]() $N_1 \leq N_2$
, we let
$N_1 \leq N_2$
, we let
 \begin{equation} \mathcal G_\varepsilon (t)= \left\{ \left| \mathcal{Z}_t- \alpha t \right| < \varepsilon \alpha t \right\}, \text{ and } \mathcal G_\varepsilon(N_1, N_2) = \bigcap_{t=N_1}^{N_2}\mathcal G_\varepsilon(t).\end{equation}
\begin{equation} \mathcal G_\varepsilon (t)= \left\{ \left| \mathcal{Z}_t- \alpha t \right| < \varepsilon \alpha t \right\}, \text{ and } \mathcal G_\varepsilon(N_1, N_2) = \bigcap_{t=N_1}^{N_2}\mathcal G_\varepsilon(t).\end{equation}
Moreover, for
![]() $t \geq 1$
, we denote by
$t \geq 1$
, we denote by
![]() $\mathscr T_{t}$
the
$\mathscr T_{t}$
the
![]() $\sigma$
-field generated by
$\sigma$
-field generated by
![]() $({\mathcal{T}}_s)_{1 \leq s \leq t}$
, containing all the information generated by the process up to time t. By the assumption of almost sure convergence and Egorov’s theorem, for any
$({\mathcal{T}}_s)_{1 \leq s \leq t}$
, containing all the information generated by the process up to time t. By the assumption of almost sure convergence and Egorov’s theorem, for any
![]() $\delta, \varepsilon > 0$
, there exists
$\delta, \varepsilon > 0$
, there exists
![]() $N^{\prime} = N^{\prime}(\varepsilon, \delta)$
such that, for all
$N^{\prime} = N^{\prime}(\varepsilon, \delta)$
such that, for all
![]() $t \geq N^{\prime}$
,
$t \geq N^{\prime}$
,
![]() ${{\mathbb{P}\!\left({\mathcal G_\varepsilon(N^{\prime}, t)}\right)}} \geq 1- \delta$
. Thus, for
${{\mathbb{P}\!\left({\mathcal G_\varepsilon(N^{\prime}, t)}\right)}} \geq 1- \delta$
. Thus, for
![]() $t \geq N^{\prime}/\eta$
, we have
$t \geq N^{\prime}/\eta$
, we have
 \begin{align} {{\mathbb{E}\!\left[{N_{\eta, k}(t,B)} \right]}} &\leq {{\mathbb{E}\!\left[{N_{\eta, k}(t,B) \mathbf{1}_{\mathcal{G}_{\varepsilon}(N^{\prime},t)}} \right]}} + \ell t\!\left(1-{{\mathbb{P}\!\left({\mathcal G_\varepsilon(N^{\prime}, t)}\right)}} \right)\\& \leq \ell \left(\sum_{\eta t < i_0 \leq t} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0,t)}\right)}} + \delta t \right).\nonumber \end{align}
\begin{align} {{\mathbb{E}\!\left[{N_{\eta, k}(t,B)} \right]}} &\leq {{\mathbb{E}\!\left[{N_{\eta, k}(t,B) \mathbf{1}_{\mathcal{G}_{\varepsilon}(N^{\prime},t)}} \right]}} + \ell t\!\left(1-{{\mathbb{P}\!\left({\mathcal G_\varepsilon(N^{\prime}, t)}\right)}} \right)\\& \leq \ell \left(\sum_{\eta t < i_0 \leq t} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0,t)}\right)}} + \delta t \right).\nonumber \end{align}
We use the shorthand
![]() $\alpha_{\pm \varepsilon} \,:\!=\, (1 \pm \varepsilon) \alpha$
.
$\alpha_{\pm \varepsilon} \,:\!=\, (1 \pm \varepsilon) \alpha$
.
Proposition 4.3. Let
![]() $B \in {\mathscr{F}}$
and
$B \in {\mathscr{F}}$
and
![]() $0 < \varepsilon, \eta \leq 1/2$
. As
$0 < \varepsilon, \eta \leq 1/2$
. As
![]() $t \to \infty$
, uniformly in
$t \to \infty$
, uniformly in
![]() $\eta t < i_0 \leq t -k$
,
$\eta t < i_0 \leq t -k$
,
![]() ${\mathcal{I}}_k = \{i_1, \ldots, i_k\}\in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
, and the choice of
${\mathcal{I}}_k = \{i_1, \ldots, i_k\}\in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
, and the choice of
![]() $\varepsilon$
, we have
$\varepsilon$
, we have
 \begin{align*}& {{\mathbb{P}\!\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0,t)}\right)}}\\ & \leq \left(1 + O(1/t) \right) {{\mathbb{E}\!\left[{\left(\frac{i_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \left( \frac{i_{s}}{i_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)} \mathbf{1}_{B}(W)} \right]}}.\end{align*}
\begin{align*}& {{\mathbb{P}\!\left({{\mathcal{E}}_{i}({\mathcal{I}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0,t)}\right)}}\\ & \leq \left(1 + O(1/t) \right) {{\mathbb{E}\!\left[{\left(\frac{i_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \left( \frac{i_{s}}{i_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)} \mathbf{1}_{B}(W)} \right]}}.\end{align*}
Corollary 4.2. Let
![]() $B \in {\mathscr{F}}$
and
$B \in {\mathscr{F}}$
and
![]() $0 < \delta, \varepsilon, \eta \leq 1/2$
. Then there exists
$0 < \delta, \varepsilon, \eta \leq 1/2$
. Then there exists
![]() $N = N(\delta, \varepsilon, \eta)$
such that, for all
$N = N(\delta, \varepsilon, \eta)$
such that, for all
![]() $t \geq N$
,
$t \geq N$
,
 \begin{align*}& \frac{{{\mathbb{E}\!\left[{N_{\eta, k}(t,B)} \right]}}}{\ell t} \leq (1+\delta) \left(\frac{1+\varepsilon}{1-\varepsilon}\right)^k {{\mathbb{E}\!\left[{ \frac{\alpha_{+\varepsilon}}{f(k, W)+\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \frac{f(s, W)}{f(s, W)+\alpha_{+\varepsilon}} \mathbf{1}_{B}(W)} \right]}}\nonumber\\& \qquad\qquad\qquad + C \eta^{1/(k+2)} + \delta,\end{align*}
\begin{align*}& \frac{{{\mathbb{E}\!\left[{N_{\eta, k}(t,B)} \right]}}}{\ell t} \leq (1+\delta) \left(\frac{1+\varepsilon}{1-\varepsilon}\right)^k {{\mathbb{E}\!\left[{ \frac{\alpha_{+\varepsilon}}{f(k, W)+\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \frac{f(s, W)}{f(s, W)+\alpha_{+\varepsilon}} \mathbf{1}_{B}(W)} \right]}}\nonumber\\& \qquad\qquad\qquad + C \eta^{1/(k+2)} + \delta,\end{align*}
where the constant C may depend on k and B but not on n and not on the choices of
![]() $\delta, \varepsilon, \eta$
. In particular, for each
$\delta, \varepsilon, \eta$
. In particular, for each
![]() $B \in \mathscr{F}$
and
$B \in \mathscr{F}$
and
![]() $k \in \mathbb{N}_0$
,
$k \in \mathbb{N}_0$
,
Proof. This follows from applying (32) and Proposition 4.3 and then applying Corollary 4.1 with
![]() $e_j = f(j,W)/\alpha_{+\varepsilon}$
and
$e_j = f(j,W)/\alpha_{+\varepsilon}$
and
![]() $f_j = f(j,W)/\alpha_{-\varepsilon}$
to bound the sum over the collection of indices. Note that the term
$f_j = f(j,W)/\alpha_{-\varepsilon}$
to bound the sum over the collection of indices. Note that the term
![]() $\left(\frac{1 + \varepsilon}{1-\varepsilon}\right)^k$
comes from replacing
$\left(\frac{1 + \varepsilon}{1-\varepsilon}\right)^k$
comes from replacing
![]() $\alpha_{-\varepsilon}$
by
$\alpha_{-\varepsilon}$
by
![]() $\alpha_{+\varepsilon}$
.
$\alpha_{+\varepsilon}$
.
We proceed towards the proof of Proposition 4.3. Let
![]() $\varepsilon, \eta$
be given such that
$\varepsilon, \eta$
be given such that
![]() $0 < \varepsilon, \eta \leq 1/2$
. For
$0 < \varepsilon, \eta \leq 1/2$
. For
![]() $\eta t < i_0 \leq t $
and
$\eta t < i_0 \leq t $
and
![]() ${\mathcal{I}}_k = \{i_1, \ldots, i_k\} \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
, for each
${\mathcal{I}}_k = \{i_1, \ldots, i_k\} \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
, for each
![]() $s \in \left\{i_0 +1, \ldots, t\right\}$
we define
$s \in \left\{i_0 +1, \ldots, t\right\}$
we define
 \begin{equation*} {\mathcal{D}}_{s} \,:\!=\,\begin{cases}\left\{i{\rightarrow} s\right\} & \text{ if } s\in{\mathcal{I}}_k,\\\left\{i{\not \rightarrow} s\right\} & \text{ otherwise},\end{cases} \end{equation*}
\begin{equation*} {\mathcal{D}}_{s} \,:\!=\,\begin{cases}\left\{i{\rightarrow} s\right\} & \text{ if } s\in{\mathcal{I}}_k,\\\left\{i{\not \rightarrow} s\right\} & \text{ otherwise},\end{cases} \end{equation*}
and
![]() $\tilde {\mathcal{D}}_s = {\mathcal{D}}_s \cap \mathcal G_{\varepsilon}(s).$
We also define
$\tilde {\mathcal{D}}_s = {\mathcal{D}}_s \cap \mathcal G_{\varepsilon}(s).$
We also define
![]() $\tilde {\mathcal{D}}_{i_0} = \mathcal G_\varepsilon(i_0) \cap \{W_i \in B\}$
, and for simplicity of notation we write
$\tilde {\mathcal{D}}_{i_0} = \mathcal G_\varepsilon(i_0) \cap \{W_i \in B\}$
, and for simplicity of notation we write
![]() $D_j$
and
$D_j$
and
![]() $\tilde D_j$
for the indicator random variables
$\tilde D_j$
for the indicator random variables
![]() $\mathbf{1}_{{\mathcal{D}}_j}$
and
$\mathbf{1}_{{\mathcal{D}}_j}$
and
![]() $\mathbf{1}_{\tilde {\mathcal{D}}_j}$
, respectively. Note that
$\mathbf{1}_{\tilde {\mathcal{D}}_j}$
, respectively. Note that
![]() $\mathcal E_i({\mathcal{I}}_k, B) \cap \mathcal G_\varepsilon(i_0,t) = \bigcap_{j=i_0}^t \tilde {\mathcal{D}}_j$
. To bound the probability of this event, we define
$\mathcal E_i({\mathcal{I}}_k, B) \cap \mathcal G_\varepsilon(i_0,t) = \bigcap_{j=i_0}^t \tilde {\mathcal{D}}_j$
. To bound the probability of this event, we define
 \begin{equation*} X_s = {{\mathbb{E}\!\left[{\prod_{j=i_{s}+1}^{t} \tilde D_j \; \bigg | \; \mathscr T_{i_s}} \right]}} \tilde D_{i_s},\quad s \in \left\{0, \ldots, k\right\}\end{equation*}
\begin{equation*} X_s = {{\mathbb{E}\!\left[{\prod_{j=i_{s}+1}^{t} \tilde D_j \; \bigg | \; \mathscr T_{i_s}} \right]}} \tilde D_{i_s},\quad s \in \left\{0, \ldots, k\right\}\end{equation*}
and observe that
![]() ${{\mathbb{E}\!\left[{X_0} \right]}} = {{\mathbb{P}\!\left({\bigcap_{s=i_0}^t \tilde {\mathcal{D}}_s}\right)}}$
is the probability we seek.
${{\mathbb{E}\!\left[{X_0} \right]}} = {{\mathbb{P}\!\left({\bigcap_{s=i_0}^t \tilde {\mathcal{D}}_s}\right)}}$
is the probability we seek.
Lemma 4.2. For
![]() $s \in \left\{0, \ldots, k\right\}$
, we have
$s \in \left\{0, \ldots, k\right\}$
, we have
 \begin{equation} X_s \leq \prod_{u=i_{k}+1}^{n} \left(1 - \frac{f(k,W)}{\alpha_{+\varepsilon}(u- 1)}\right) \left(\prod_{j = s}^{k-1} \frac{f(j,W)}{\alpha_{-\varepsilon}(i_{j+1}-1)}\prod_{j^{\prime}= i_j +1}^{i_{j+1} -1} \left(1 - \frac{f(j,W)}{\alpha_{+\varepsilon}(j^{\prime} -1)}\right)\right)\tilde{D}_{i_s},\end{equation}
\begin{equation} X_s \leq \prod_{u=i_{k}+1}^{n} \left(1 - \frac{f(k,W)}{\alpha_{+\varepsilon}(u- 1)}\right) \left(\prod_{j = s}^{k-1} \frac{f(j,W)}{\alpha_{-\varepsilon}(i_{j+1}-1)}\prod_{j^{\prime}= i_j +1}^{i_{j+1} -1} \left(1 - \frac{f(j,W)}{\alpha_{+\varepsilon}(j^{\prime} -1)}\right)\right)\tilde{D}_{i_s},\end{equation}
where we interpret any empty products (for example when
![]() $i_k = n$
) as equal to 1. In particular,
$i_k = n$
) as equal to 1. In particular,
 \begin{align}{{\mathbb{E}\!\left[{X_0} \right]}} &\leq {{\mathbb{E}\!\left[{\prod_{u=i_{k}+1}^{n}\!\! \left(1 - \frac{f(k,W)}{\alpha_{+\varepsilon}(u- 1)}\right) \left(\prod_{j = 0}^{k-1} \frac{f(j,W)}{\alpha_{-\varepsilon}(i_{j+1}-1)} \prod_{j^{\prime}= i_j +1}^{i_{j+1} -1} \!\left(1 - \frac{f(j,W)}{\alpha_{+\varepsilon}(j^{\prime} -1)}\right)\!\right) \mathbf{1}_{B}(W)} \right]}}. \qquad\end{align}
\begin{align}{{\mathbb{E}\!\left[{X_0} \right]}} &\leq {{\mathbb{E}\!\left[{\prod_{u=i_{k}+1}^{n}\!\! \left(1 - \frac{f(k,W)}{\alpha_{+\varepsilon}(u- 1)}\right) \left(\prod_{j = 0}^{k-1} \frac{f(j,W)}{\alpha_{-\varepsilon}(i_{j+1}-1)} \prod_{j^{\prime}= i_j +1}^{i_{j+1} -1} \!\left(1 - \frac{f(j,W)}{\alpha_{+\varepsilon}(j^{\prime} -1)}\right)\!\right) \mathbf{1}_{B}(W)} \right]}}. \qquad\end{align}
Proof. We prove (33) by backwards induction. For the base case,
![]() $s=k$
, if
$s=k$
, if
![]() $i_k = n$
, the inequality is trivial, as
$i_k = n$
, the inequality is trivial, as
![]() $X_k = \tilde{D}_{i_k}$
. Thus, assuming
$X_k = \tilde{D}_{i_k}$
. Thus, assuming
![]() $i_k < n$
, by the tower property,
$i_k < n$
, by the tower property,
 \begin{align*}{{\mathbb{E}\!\left[{\prod_{j=i_{k}+1}^{n} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} & = {{\mathbb{E} \!\left[{{{\mathbb{E}\!\left[{\tilde D_{n} \; \bigg | \; \mathscr{T}_{n-1}} \right]}}\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &\leq {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{n} \; \bigg | \; \mathscr{T}_{n-1}} \right]}}\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &= {{\mathbb{E}\!\left[{\left(1 - \frac{f(k,W)}{\mathcal{Z}_{n-1}}\right)\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &\leq \left(1 - \frac{f(k,W)}{ \alpha_{+\varepsilon}(n-1)}\right) {{\mathbb{E}\!\left[{\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}},\end{align*}
\begin{align*}{{\mathbb{E}\!\left[{\prod_{j=i_{k}+1}^{n} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} & = {{\mathbb{E} \!\left[{{{\mathbb{E}\!\left[{\tilde D_{n} \; \bigg | \; \mathscr{T}_{n-1}} \right]}}\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &\leq {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{n} \; \bigg | \; \mathscr{T}_{n-1}} \right]}}\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &= {{\mathbb{E}\!\left[{\left(1 - \frac{f(k,W)}{\mathcal{Z}_{n-1}}\right)\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}} \\ &\leq \left(1 - \frac{f(k,W)}{ \alpha_{+\varepsilon}(n-1)}\right) {{\mathbb{E}\!\left[{\prod_{j=i_k+1}^{n-1} \tilde D_j \; \bigg | \; \mathscr T_{i_k}} \right]}},\end{align*}
and iterating this argument with the conditional expectation on the right-hand side proves the base case. Now, note that for
![]() $s \in \left\{0, \ldots, k-1\right\}$
$s \in \left\{0, \ldots, k-1\right\}$
 \begin{equation*}X_s = {{\mathbb{E}\!\left[{X_{s+1} \prod_{j=i_{s} +1}^{i_{s+1} -1} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}} \right]}} \tilde D_{i_s}.\end{equation*}
\begin{equation*}X_s = {{\mathbb{E}\!\left[{X_{s+1} \prod_{j=i_{s} +1}^{i_{s+1} -1} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}} \right]}} \tilde D_{i_s}.\end{equation*}
Applying the induction hypothesis, it suffices to bound the term
![]() ${{\mathbb{E}\!\left[{\prod_{j=i_{s} +1}^{i_{s+1}} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}$
, and, similarly to the base case, we may assume
${{\mathbb{E}\!\left[{\prod_{j=i_{s} +1}^{i_{s+1}} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}$
, and, similarly to the base case, we may assume
![]() $i_{s} < i_{s+1} - 1$
. But then we have
$i_{s} < i_{s+1} - 1$
. But then we have
 \begin{align*}{{\mathbb{E}\!\left[{\prod_{j=i_{s} +1}^{i_{s+1}} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}} \right]}} & = {{\mathbb{E} \!\left[{{{\mathbb{E}\!\left[{\tilde D_{i_{s+1}} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}} \right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}} \\ &\leq {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{i_{s+1}} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}}\right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ &\leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}{{\mathbb{E}\!\left[{\prod_{j=i_s + 1}^{i_{s+1}-2} \tilde{D}_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ & \leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}{{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{i_{s+1} -1} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}}\right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ & \leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}\left(1 - \frac{f(s,W)}{\alpha_{+\varepsilon} \left(i_{s+1} -2\right) } \right) {{\mathbb{E}\!\left[{ \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}.\end{align*}
\begin{align*}{{\mathbb{E}\!\left[{\prod_{j=i_{s} +1}^{i_{s+1}} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}} \right]}} & = {{\mathbb{E} \!\left[{{{\mathbb{E}\!\left[{\tilde D_{i_{s+1}} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}} \right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}} \\ &\leq {{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{i_{s+1}} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}}\right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ &\leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}{{\mathbb{E}\!\left[{\prod_{j=i_s + 1}^{i_{s+1}-2} \tilde{D}_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ & \leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}{{\mathbb{E}\!\left[{{{\mathbb{E}\!\left[{D_{i_{s+1} -1} \; \bigg | \; \mathscr{T}_{i_{s+1} -1}}\right]}} \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}\\ & \leq \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1} - 1)}\left(1 - \frac{f(s,W)}{\alpha_{+\varepsilon} \left(i_{s+1} -2\right) } \right) {{\mathbb{E}\!\left[{ \prod_{j=i_{s} +1}^{i_{s+1}-2} \tilde D_{j} \; \bigg | \; \mathscr T_{i_s}}\right]}}.\end{align*}
Iterating these bounds, the inductive step follows in a similar manner to the base case. Finally, noting that
![]() $\mathbf{1}_{\tilde{\mathcal{D}}_{i}} \leq \mathbf{1}_{B}(W)$
proves (34).
$\mathbf{1}_{\tilde{\mathcal{D}}_{i}} \leq \mathbf{1}_{B}(W)$
proves (34).
The next lemma follows from a simple application of Stirling’s formula, i.e., (25).
Lemma 4.3. Let
![]() $\eta, C > 0$
. Then, uniformly over
$\eta, C > 0$
. Then, uniformly over
![]() $\eta t \leq a \leq b$
and
$\eta t \leq a \leq b$
and
![]() $0 \leq \beta \leq C$
, we have
$0 \leq \beta \leq C$
, we have
 \begin{equation*}\prod_{j=a+1}^{b-1} \left(1-\frac{\beta}{j-1}\right) = \left(\frac{a}{b}\right)^\beta \left( 1 + O\!\left(\frac 1 t\right) \right).\end{equation*}
\begin{equation*}\prod_{j=a+1}^{b-1} \left(1-\frac{\beta}{j-1}\right) = \left(\frac{a}{b}\right)^\beta \left( 1 + O\!\left(\frac 1 t\right) \right).\end{equation*}
4.4. Deducing convergence of the mean of
 $N_{k}(t,B)/\ell t$
$N_{k}(t,B)/\ell t$
In this subsection we deduce a lower bound on
![]() $\liminf_{t \to \infty} {{\mathbb{E}\!\left[{N_k(t,B)}\right]}}/ \ell t$
on measurable sets
$\liminf_{t \to \infty} {{\mathbb{E}\!\left[{N_k(t,B)}\right]}}/ \ell t$
on measurable sets
![]() $B \in {\mathscr{F}}$
. In what follows, denote by
$B \in {\mathscr{F}}$
. In what follows, denote by
![]() $N_{\geq M}(t,B)$
the number of vertices of out-degree
$N_{\geq M}(t,B)$
the number of vertices of out-degree
![]() $\geq \ell M$
with weight belonging to B. Moreover, let
$\geq \ell M$
with weight belonging to B. Moreover, let
![]() $N(t,B) = N_{\geq 0}(t,B)$
denote the total number of vertices at time t with weight belonging to B.
$N(t,B) = N_{\geq 0}(t,B)$
denote the total number of vertices at time t with weight belonging to B.
Lemma 4.4. For any measurable set B, we have
almost surely.
Proof. Since we add
![]() $\ell$
vertices at each time-step, we have
$\ell$
vertices at each time-step, we have
![]() $\limsup_{t \to \infty} \frac{\left|\mathcal{T}_{t}\right|}{\ell t} = 1$
. However,
$\limsup_{t \to \infty} \frac{\left|\mathcal{T}_{t}\right|}{\ell t} = 1$
. However,
![]() $\left | \mathcal{T}_t \right | \geq M N_{\geq M}(t, \mathbb{R})$
, since the right-hand side only provides a lower bound for the number of vertices in the tree incident to those with out-degree at least M. The result follows from dividing both sides by
$\left | \mathcal{T}_t \right | \geq M N_{\geq M}(t, \mathbb{R})$
, since the right-hand side only provides a lower bound for the number of vertices in the tree incident to those with out-degree at least M. The result follows from dividing both sides by
![]() $M \ell t$
and sending t to infinity.
$M \ell t$
and sending t to infinity.
4.4.1. Proof of Proposition 4.1
Proof. Recall that Corollary 4.2 showed that for each
![]() $B \in \mathscr{F}$
and
$B \in \mathscr{F}$
and
![]() $k \in \mathbb{N}_0$
,
$k \in \mathbb{N}_0$
,
Now, suppose that Proposition 4.1 fails, so that in particular there exist some set
![]() $B^{\prime} \in \mathscr{F}$
and some
$B^{\prime} \in \mathscr{F}$
and some
![]() $k^{\prime} \in \mathbb{N}_{0}$
such that
$k^{\prime} \in \mathbb{N}_{0}$
such that
Thus, for some
![]() $\epsilon^{\prime} > 0$
, we have
$\epsilon^{\prime} > 0$
, we have
Now, using Lemma 4.4, choose
![]() $M > \max{\left \{k^{\prime}, \frac{2}{\epsilon^{\prime}}\right \}}$
, so that
$M > \max{\left \{k^{\prime}, \frac{2}{\epsilon^{\prime}}\right \}}$
, so that
Then, recalling (13),
 \begin{align}\liminf_{t \to \infty} {{\mathbb{E}\!\left[{\sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}}\right]}} & \leq \liminf_{t \to \infty} {{\mathbb{E}\!\left[{\frac{N_{k^{\prime}}(t,B^{\prime})}{\ell t}} \right]}} + \sum_{k \neq k^{\prime}} \limsup_{t \to \infty} {{\mathbb{E} \!\left[{\frac{N_{k}(t,B^{\prime})}{\ell t}} \right]}}\\ & \leq \left(\sum_{k=0}^{\infty} p^{\alpha}_{k}(B^{\prime})\right) - \epsilon^{\prime} \leq \mu(B^{\prime}) - \epsilon^{\prime}.\nonumber\end{align}
\begin{align}\liminf_{t \to \infty} {{\mathbb{E}\!\left[{\sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}}\right]}} & \leq \liminf_{t \to \infty} {{\mathbb{E}\!\left[{\frac{N_{k^{\prime}}(t,B^{\prime})}{\ell t}} \right]}} + \sum_{k \neq k^{\prime}} \limsup_{t \to \infty} {{\mathbb{E} \!\left[{\frac{N_{k}(t,B^{\prime})}{\ell t}} \right]}}\\ & \leq \left(\sum_{k=0}^{\infty} p^{\alpha}_{k}(B^{\prime})\right) - \epsilon^{\prime} \leq \mu(B^{\prime}) - \epsilon^{\prime}.\nonumber\end{align}
On the other hand, by Fatou’s lemma, we have
 \begin{align}\liminf_{t \to \infty} {{\mathbb{E}\!\left[{\sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}}\right]}} & \geq {{\mathbb{E} \!\left[{\liminf_{t \to \infty} \sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}} \right]}} \end{align}
\begin{align}\liminf_{t \to \infty} {{\mathbb{E}\!\left[{\sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}}\right]}} & \geq {{\mathbb{E} \!\left[{\liminf_{t \to \infty} \sum_{k=0}^{M} \frac{N_{k}(t,B^{\prime})}{\ell t}} \right]}} \end{align}
where the last inequality follows from the strong law of large numbers. But then, combining (35) and (36), we have
![]() $\mu(B^{\prime}) - \epsilon^{\prime} \geq \mu(B^{\prime}) - \epsilon^{\prime}/2$
, a contradiction.
$\mu(B^{\prime}) - \epsilon^{\prime} \geq \mu(B^{\prime}) - \epsilon^{\prime}/2$
, a contradiction.
4.5. Second moment calculations
In order to bound the second moment, we apply calculations similar to those at the start of the section to compute asymptotically the number of pairs of vertices of out-degree
![]() $k \ell$
born after time
$k \ell$
born after time
![]() $\eta t$
. For vertices i and j, as in Section 4.3, we set
$\eta t$
. For vertices i and j, as in Section 4.3, we set
![]() $i_0 \,:\!=\, \lfloor i/\ell \rfloor$
and
$i_0 \,:\!=\, \lfloor i/\ell \rfloor$
and
![]() $j_0 \,:\!=\, \lfloor j/\ell \rfloor$
, and note that
$j_0 \,:\!=\, \lfloor j/\ell \rfloor$
, and note that
Note that, in a similar manner to (30), we have
 \begin{equation*}{{\mathbb{E}\!\left[{\left|\frac{\left(N_{\eta, k}(t,B)\right)^2}{\ell^2 t^2} - \frac{\left(N_{k}(t,B)\right)^2}{\ell^2 t^2}\right|}\right]}} \leq \eta, \end{equation*}
\begin{equation*}{{\mathbb{E}\!\left[{\left|\frac{\left(N_{\eta, k}(t,B)\right)^2}{\ell^2 t^2} - \frac{\left(N_{k}(t,B)\right)^2}{\ell^2 t^2}\right|}\right]}} \leq \eta, \end{equation*}
so that it suffices to prove that
 \begin{equation*}\limsup_{\eta \to 0} \limsup_{t \to \infty} {{\mathbb{E}\!\left[{\frac{\left(N_{\eta, k}(t, B)\right)^2}{\ell^2 t^2}}\right]}} \leq (p^{\alpha}_{k}(B))^2.\end{equation*}
\begin{equation*}\limsup_{\eta \to 0} \limsup_{t \to \infty} {{\mathbb{E}\!\left[{\frac{\left(N_{\eta, k}(t, B)\right)^2}{\ell^2 t^2}}\right]}} \leq (p^{\alpha}_{k}(B))^2.\end{equation*}
Recall that, for a given i, we denote by
![]() ${\mathcal{I}}_k$
a collection of natural numbers
${\mathcal{I}}_k$
a collection of natural numbers
![]() $i_0 < i_1 < \cdots < i_k \leq t$
. Moreover, for a given j, we denote by
$i_0 < i_1 < \cdots < i_k \leq t$
. Moreover, for a given j, we denote by
![]() ${\mathcal{J}}_{k}$
a collection of natural numbers
${\mathcal{J}}_{k}$
a collection of natural numbers
![]() $j_0 < j_1 < \cdots < j_k \leq t$
. Similarly to Section 4.3, for
$j_0 < j_1 < \cdots < j_k \leq t$
. Similarly to Section 4.3, for
![]() $s > j$
we use the notation
$s > j$
we use the notation
![]() $j {\rightarrow} s$
to denote that j is the vertex chosen at the sth time-step, and likewise, we let
$j {\rightarrow} s$
to denote that j is the vertex chosen at the sth time-step, and likewise, we let
![]() ${\mathcal{E}}_{j}({\mathcal{J}}_k, B)$
denote the event that
${\mathcal{E}}_{j}({\mathcal{J}}_k, B)$
denote the event that
![]() $W_j \in B$
and for all
$W_j \in B$
and for all
![]() $s \in \left\{j_0 +1, \ldots, t\right\}$
,
$s \in \left\{j_0 +1, \ldots, t\right\}$
,
![]() $j {\rightarrow} s$
if and only if
$j {\rightarrow} s$
if and only if
![]() $s \in {\mathcal{J}}_k$
. Then we have
$s \in {\mathcal{J}}_k$
. Then we have
 \begin{align*}&\mathbb{P}\left({d_{i}(t) = k, W_i \in B, d_{j}(t) = k, W_j \in B}\right)\\& \qquad \qquad \qquad = \sum_{{\mathcal{J}}_k \in \tiny\left(\begin{array}{c}\left\{j_0 +1, \ldots, t\right\}\\k\end{array}\right)} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B)}\right)}}.\end{align*}
\begin{align*}&\mathbb{P}\left({d_{i}(t) = k, W_i \in B, d_{j}(t) = k, W_j \in B}\right)\\& \qquad \qquad \qquad = \sum_{{\mathcal{J}}_k \in \tiny\left(\begin{array}{c}\left\{j_0 +1, \ldots, t\right\}\\k\end{array}\right)} \sum_{{\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)} {{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B)}\right)}}.\end{align*}
Note that the contribution to the above sum corresponding to terms with
![]() ${\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} \neq \varnothing$
, and
${\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} \neq \varnothing$
, and
![]() $i \neq j$
, is zero, since it is impossible for distinct vertices to be chosen in a single time-step. But then, the terms corresponding to
$i \neq j$
, is zero, since it is impossible for distinct vertices to be chosen in a single time-step. But then, the terms corresponding to
![]() $i = j$
contribute at most
$i = j$
contribute at most
![]() ${{\mathbb{E}\!\left[{N_{\eta,k}(n, B)}\right]}} \leq \ell n$
to the right side of (37). Next, for any choice of indices with
${{\mathbb{E}\!\left[{N_{\eta,k}(n, B)}\right]}} \leq \ell n$
to the right side of (37). Next, for any choice of indices with
![]() ${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
, there are at most
${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
, there are at most
![]() $\ell^2$
pairs of vertices (i, j) born at respective times
$\ell^2$
pairs of vertices (i, j) born at respective times
![]() $(i_0, j_0)$
contributing to the sum in (37). Recalling the definitions of
$(i_0, j_0)$
contributing to the sum in (37). Recalling the definitions of
![]() $\mathcal{G}_{\varepsilon}(t)$
,
$\mathcal{G}_{\varepsilon}(t)$
,
![]() $\mathcal{G}_{\varepsilon}(N_1,N_2)$
, and
$\mathcal{G}_{\varepsilon}(N_1,N_2)$
, and
![]() $N^{\prime} = N^{\prime}(\varepsilon, \delta)$
from (31) and below in the previous subsection, in a similar manner to (32) we have, for
$N^{\prime} = N^{\prime}(\varepsilon, \delta)$
from (31) and below in the previous subsection, in a similar manner to (32) we have, for
![]() $t \geq N^{\prime}/\eta$
,
$t \geq N^{\prime}/\eta$
,
 \begin{equation} {{\mathbb{E}\!\left[{\left(N_{\eta, k}(t, B) \right)^2}\right]}} \leq \ell^2 \left( \sum_{\eta t < i_0, j_0 \leq t-k} \sum_{{{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}} {{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0, t)}\right)}} + \delta t^2\right) + \ell t.\end{equation}
\begin{equation} {{\mathbb{E}\!\left[{\left(N_{\eta, k}(t, B) \right)^2}\right]}} \leq \ell^2 \left( \sum_{\eta t < i_0, j_0 \leq t-k} \sum_{{{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}} {{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0, t)}\right)}} + \delta t^2\right) + \ell t.\end{equation}
We then have the following.
Proposition 4.4. Let
![]() $B \in {\mathscr{F}}$
and
$B \in {\mathscr{F}}$
and
![]() $0 < \varepsilon, \eta \leq 1/2$
. As
$0 < \varepsilon, \eta \leq 1/2$
. As
![]() $t \to \infty$
, uniformly in
$t \to \infty$
, uniformly in
![]() $\eta t < i_0 \leq j_0 \leq t -k$
, in
$\eta t < i_0 \leq j_0 \leq t -k$
, in
![]() ${\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
,
${\mathcal{I}}_k \in \tiny\left(\begin{array}{c}\left\{i_0 +1, \ldots, t\right\}\\k\end{array}\right)$
,
![]() ${\mathcal{J}}_k \in \tiny\left(\begin{array}{c}\left\{j_0+1, \ldots, t\right\}\\k\end{array}\right)$
such that
${\mathcal{J}}_k \in \tiny\left(\begin{array}{c}\left\{j_0+1, \ldots, t\right\}\\k\end{array}\right)$
such that
![]() ${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
, and in the choice of
${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
, and in the choice of
![]() $\varepsilon$
, we have
$\varepsilon$
, we have
 \begin{align} & \nonumber{{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0, t)}\right)}} \nonumber\\ & \qquad\qquad \leq (1 + O(1/t)) {{\mathbb{E}\!\left[{\left(\frac{i_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\left( \frac{i_{s}}{i_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1}-1)}\right) \mathbf{1}_{B}(W)}\right]}}\nonumber\\ & \qquad\qquad \times {{\mathbb{E}\!\left[{\left(\frac{j_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\left( \frac{j_{s}}{j_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(j_{s+1}-1}\right)\mathbf{1}_{B}(W)}\right]}}.\end{align}
\begin{align} & \nonumber{{\mathbb{P}\!\left({{\mathcal{E}}_i({\mathcal{I}}_k,B) \cap {\mathcal{E}}_j({\mathcal{J}}_k, B) \cap \mathcal{G}_{\varepsilon}(i_0, t)}\right)}} \nonumber\\ & \qquad\qquad \leq (1 + O(1/t)) {{\mathbb{E}\!\left[{\left(\frac{i_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\left( \frac{i_{s}}{i_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(i_{s+1}-1)}\right) \mathbf{1}_{B}(W)}\right]}}\nonumber\\ & \qquad\qquad \times {{\mathbb{E}\!\left[{\left(\frac{j_{k}}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\left( \frac{j_{s}}{j_{s +1}}\right)^{f(s, W)/\alpha_{+\varepsilon}} \frac{f(s,W)}{\alpha_{-\varepsilon}(j_{s+1}-1}\right)\mathbf{1}_{B}(W)}\right]}}.\end{align}
We leave the details of the proof of this proposition to the reader, as it follows an analogous approach to the proof of Proposition 4.3, using a backwards induction argument.
Proof. sketch. Let
![]() $u_1, \ldots, u_{2k}$
denote the indices in
$u_1, \ldots, u_{2k}$
denote the indices in
![]() ${\mathcal{I}}_k \cup {\mathcal{J}}_k$
, and let
${\mathcal{I}}_k \cup {\mathcal{J}}_k$
, and let
![]() $f_x(i), f_{x}(j)$
denote the fitnesses associated with vertex i and vertex j at time x. Then, when we bound the probabilities
$f_x(i), f_{x}(j)$
denote the fitnesses associated with vertex i and vertex j at time x. Then, when we bound the probabilities
![]() $\{i {\not \rightarrow} x \} \cap \{j {\not\rightarrow} x\}$
for all
$\{i {\not \rightarrow} x \} \cap \{j {\not\rightarrow} x\}$
for all
![]() $x \in \left\{u_{s} +1, \ldots, u_{s+1} - 1\right\}$
from above, we obtain terms of the form
$x \in \left\{u_{s} +1, \ldots, u_{s+1} - 1\right\}$
from above, we obtain terms of the form
 \begin{equation*}\prod_{x = u_{s}+1}^{u_{s+1} - 1} \left(1 - \frac{f_{x}(i) + f_{x}(j)}{\alpha_{+\varepsilon}(x-1)} \right) = \left(\frac{u_{s}}{u_{s+1}} \right)^{f_{x}(i) + f_{x}(j)} \left(1+ O\!\left(\frac{1}{t}\right)\right),\end{equation*}
\begin{equation*}\prod_{x = u_{s}+1}^{u_{s+1} - 1} \left(1 - \frac{f_{x}(i) + f_{x}(j)}{\alpha_{+\varepsilon}(x-1)} \right) = \left(\frac{u_{s}}{u_{s+1}} \right)^{f_{x}(i) + f_{x}(j)} \left(1+ O\!\left(\frac{1}{t}\right)\right),\end{equation*}
where the right side follows from Lemma 4.3. Then, when we evaluate the expectation analogous to the expectation appearing in (34), we obtain an expectation involving products of terms dependent on
![]() $W_i$
and
$W_i$
and
![]() $W_j$
, i.e., the weights associated with vertex i and vertex j. These terms separate into a product of expectations by the independence of the random variables
$W_j$
, i.e., the weights associated with vertex i and vertex j. These terms separate into a product of expectations by the independence of the random variables
![]() $W_i$
,
$W_i$
,
![]() $W_j$
, and finally, many of the products telescope to yield the right side of (39).
$W_j$
, and finally, many of the products telescope to yield the right side of (39).
4.5.1. Proof of Proposition 4.2
Proof. We apply Proposition 4.4 to bound the summands in (38). Then, as we are looking for an upper bound, we may drop the condition
![]() ${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
when evaluating the sum. But then, by Corollary 4.1, we have, uniformly in
${{\mathcal{I}}_{k} \cap {\mathcal{J}}_{k} = \emptyset}$
when evaluating the sum. But then, by Corollary 4.1, we have, uniformly in
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $\eta$
,
$\eta$
,
 \begin{align*}& \sum_{\eta t < i_0, j_0 \leq t} \sum_{{\mathcal{I}}_k, {\mathcal{J}}_k} {{\mathbb{E} \!\left[{\left(\frac{i_k}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}}\cdot \prod_{s=0}^{k-1} \left(\frac{i_s}{i_{s+1}}\right)^{f(s,W)/\alpha_{+\varepsilon}}\frac{f(s,W)}{\alpha_{-\varepsilon} (i_{s+1}-1)} \mathbf{1}_{B}(W)} \right]}} \nonumber \nonumber \\ &\qquad\qquad\qquad \times {{\mathbb{E}\!\left[{\left(\frac{j_k}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\frac{j_s}{j_{s+1}}\right)^{f(s,W)/\alpha_{+\varepsilon}}\frac{f(s,W)}{\alpha_{-\varepsilon} (j_{s+1}-1)} \mathbf{1}_{B}(W)}\right]}} \\ & \leq \left(\frac{1+\varepsilon}{1-\varepsilon}\right)^{2k} \left( {{\mathbb{E} \!\left[{\frac{\alpha_{+\varepsilon}}{f(k,W)+\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \frac{f(s,W)}{f(s,W)+\alpha_{+\varepsilon}} \mathbf{1}_{B}(W)}\right]}} \right)^2+ O\!\left(t^{-1/(k+2)}\right) + C^{\prime}\eta^{1/{k+2}},\end{align*}
\begin{align*}& \sum_{\eta t < i_0, j_0 \leq t} \sum_{{\mathcal{I}}_k, {\mathcal{J}}_k} {{\mathbb{E} \!\left[{\left(\frac{i_k}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}}\cdot \prod_{s=0}^{k-1} \left(\frac{i_s}{i_{s+1}}\right)^{f(s,W)/\alpha_{+\varepsilon}}\frac{f(s,W)}{\alpha_{-\varepsilon} (i_{s+1}-1)} \mathbf{1}_{B}(W)} \right]}} \nonumber \nonumber \\ &\qquad\qquad\qquad \times {{\mathbb{E}\!\left[{\left(\frac{j_k}{t}\right)^{f(k,W)/\alpha_{+\varepsilon}} \cdot \prod_{s=0}^{k-1} \left(\frac{j_s}{j_{s+1}}\right)^{f(s,W)/\alpha_{+\varepsilon}}\frac{f(s,W)}{\alpha_{-\varepsilon} (j_{s+1}-1)} \mathbf{1}_{B}(W)}\right]}} \\ & \leq \left(\frac{1+\varepsilon}{1-\varepsilon}\right)^{2k} \left( {{\mathbb{E} \!\left[{\frac{\alpha_{+\varepsilon}}{f(k,W)+\alpha_{+\varepsilon}} \prod_{s=0}^{k-1} \frac{f(s,W)}{f(s,W)+\alpha_{+\varepsilon}} \mathbf{1}_{B}(W)}\right]}} \right)^2+ O\!\left(t^{-1/(k+2)}\right) + C^{\prime}\eta^{1/{k+2}},\end{align*}
for some universal constant
![]() $C^{\prime} >0$
, depending only on B, f. The result follows.
$C^{\prime} >0$
, depending only on B, f. The result follows.
Acknowledgements
I would like to thank my supervisor, Nikolaos Fountoulakis, for his guidance and useful feedback on earlier drafts. I would also like to thank Cécile Mailler and Henning Sulzbach, whose collaborative work (along with Nikolaos) on a previous project introduced me to some of the techniques used in this paper. Finally, I would like to thank the anonymous referees for their helpful comments, which greatly improved the presentation of this paper, in particular leading to the removal of some unnecessary assumptions in the statements of Theorem 3.1 and Theorem 3.2.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.